基于西门子840D数控系统的龙门五轴数控机床几何误差补偿软件开发*
周显峰 李 杰 刘辛军 陈俊宇
(①成都飞机工业(集团)有限责任公司,四川 成都 610092;②清华大学机械工程系制造工程研究所,精密超精密制造装备及控制北京市重点实验室,北京 100084;③北京大学力学与工程科学系,北京 100871)
五轴数控机床因位姿调节能力强,切削效率高,工件安装时间短等优点逐渐成为复杂工件加工的主要设备。由于复杂的机械结构和控制系统,五轴数控机床空间定位精度相比于三轴数控机床更难得到保证,工零件加工过程中尺寸超差时有发生[1]。特别是大型龙门五轴数控机床,其加工行程长,龙门跨度大,运动单元重,空间定位精度易超差,周期性误差补偿必不可少。为应对这一问题,众多机床误差建模和辨识方法被相继提出,五轴数控机床加工精度的改善成为当下研究热点[2]。几何误差是影响机床加工精度的主要因素之一[3],包括定位误差,直线度误差,颠摆、偏摆、滚摆误差及垂直度误差。在04专项支持下,笔者近几年系统性地开展了龙门五轴数控机床几何误差检测、辨识和补偿方法研究。针对平动轴,提出了十三线几何误差辨识方法[4],利用长方体空间的9条棱、3条面对角线和1条体对角线定位误差可有效计算出平动轴各项几何误差[5];针对A、C摆动轴,提出了基于偏置球心R-test的几何误差辨识方法[6],通过变更R-test偏置参数获得关于检测球头的多组空间位置误差,结合误差模型求解超静定方程组可辨识转动轴各项几何误差[7]。
在获得几何误差值的基础上,使用数控系统误差补偿列表对机床误差进行修正是减小机床空间定位误差的最有效方法之一[8]。许多知名数控系统厂家均在其推出的数控系统中支持这种补偿方法。如Fanuc 30i和Siemens 840D 误差补偿系统,采用激光干涉仪作为检测设备,在机床工作空间内采集测量数据,然后生成数控系统的误差补偿文件可实现机床几何误差的补偿[9]。虽然激光干涉仪的检测值可以直接用于定位误差补偿,但实际测量过程中直接检测是无法准确获得平动轴的全部几何误差项的(如直接测量的定位误差实际上是轴间垂直度误差、角度误差与实际定位误差的叠加)。开展机床几何误差建模,通过辨识算法求解进给轴全项几何误差,更有利于分离干扰误差项,实现机床几何误差的准确补偿。笔者经多年研究在龙门五轴数控机床几何误差建模、检测、辨识和补偿方面取得了一些研究成果[1-7,10,11],已经实现根据所提出的辨识算法获取机床的各项几何误差,然后通过数控系统误差补偿列表进行误差补偿。然而,目前误差补偿还只能以手工录入补偿数据的方法来完成,大大限制了补偿效率以及研究成果的普及。
机床空间误差补偿技术属于商业机密,国外研究机构和机床厂商鲜有文章介绍相关软件的开发,而国内基于数控系统的空间误差补偿软件尚有待开发。虽然国外已有成熟的VCS(volumetric error compensation system)软件及配套设备,但其采购和维护费高昂。若全面采用进口仪器和软件来完成机床的几何误差补偿,虽然能够解决一时之急,但长期持续成本过大而且易受国外技术牵制,同时还制约了我国自主知识产权误差补偿技术的研发。因此,研制一款具有检测数据导入、误差自动辨识、补偿文件自动生成和识别功能的几何误差补偿软件,对于机床几何误差补偿方法的应用推广具有极为重要的工程意义。本文基于笔者所提出的平动轴与摆动轴误差辨识算法[4,6],开发了一种针对Siemens 840D数控系统的几何误差补偿软件,通过导入激光干涉仪和R-test的误差检测数据[4-7,10-11]能够自动辨识机床的各项几何误差,并将辨识结果以Siemens 840D系统识别的补偿格式输出,从而通过数控系统装载补偿文件实现了几何误差自动补偿。本文首先阐述了软件的设计思路及开发环境,然后介绍了软件内部集成的辨识算法及配套检测策略,在此基础上介绍了软件的主要界面及操作流程,最后通过切削S试件验证了误差补偿软件的应用效果。
1 软件设计
功能需求、软件架构和开发环境是软件设计的三要素。根据现场应用需求调研,立足于简洁、实用的原则,本章将从功能需求分析、基本架构设计和开发环境3个方面介绍该误差补偿软件的总体设计思路。
1.1 功能分析
软件开发的主要目的在于实现测量数据导入、补偿数据计算、补偿文件生成这3个主要功能,在此基础上补充一些便于操作的辅助功能。通过对数控厂应用需求的调研,该几何误差补偿软件需要实现的主要功能如下:
(1)账号密码登陆;(2)机床及轴种类选择;(3)测量数据导入和删除;(4)测量数据图表展示;(5)计算参数导入;(6)补偿数据计算;(7)计算结果图表展示;(8)补偿系数导入;(9)补偿文件生成。
1.2 基本结构
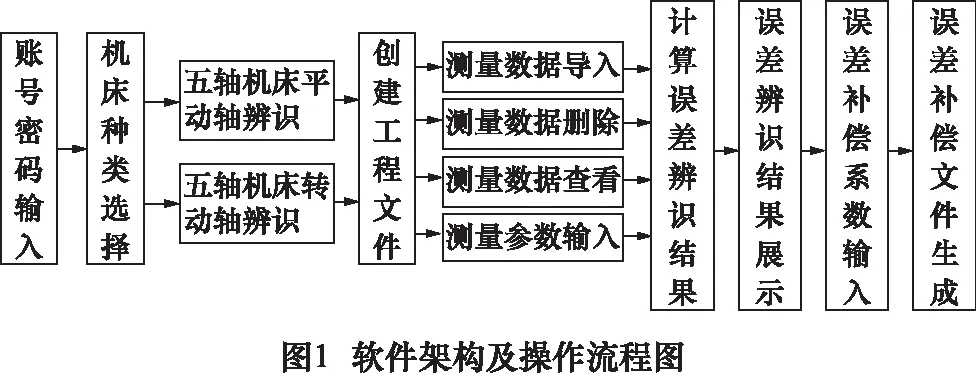
基于功能需求和使用便捷性,规划软件结构及操作流程如图1所示。首先通过账号和密码进入误差补偿软件,根据需求选择不同类型的机床(目前只有龙门五轴数控机床,其他为留用接口)。进入机床类型后,根据需要选择平动轴或转动轴进行误差辨识,并创立相应工程文件。在所创建的工程文件里进行的主要操作包括:测量数据导入(测量数据是在给定检测策略下获得[5,7])、数据查看、数据删除(修改)以及检测参数输入。完成数据导入和辨识条件配置后,即可进行几何误差辨识计算以及结果的展示。此外,可以根据工程需要通过补偿系数对补偿数据进行修正,最终由软件生成西门子数控系统识别的补偿文件。
1.3 开发环境
本软件以Windows平台为基础,选择了Qt[12]作为开发框架,Qt Creator作为开发环境,使用C++进行程序语言编写。选择C++作为编程语言能实现对数据和合法操作的封装,有利于在数值分析复杂的数据计算中保持各组数据间不会出现相互干扰。对于32位简化系统工控机运行环境,C++具有更好的兼容性。Qt是1991年由奇趣科技开发的跨平台C++图形用户界面应用程序开发框架,其良好的封装性和高模块化程度使得其各个元件之间的协同工作变得十分简单,对于开发需要进行窗口模块间反复传值调用的工业软件而言有着巨大的优势。同时,大量已经开发成型的模块可以被直接用于软件编写(如本软件中绘图部分采用的qwt[13-15]即为基于LGPL版权协议的开源项目,可生成各种统计图),从而能大大加快程序的开发速度。Qt Creator[16]是与Qt配套的集成开发环境,能够帮助Qt用户快速地入门、开发和运行项目。内部集成的Qt Designer能够方便开发人员对软件窗口进行可视化布局,同时其对Qt核心的信号槽机制也有配套的图示调节器。
2 核心算法
龙门五轴数控机床几何误差补偿软件,包括平动轴几何误差辨识、补偿模块和摆动轴几何误差辨识、补偿模块两个重要部分。由于两种进给轴的拓扑类型不同,所采用的检测策略和辨识方法都有所差异。几何误差检测方法和辨识算法是本软件算法的核心所在,本文将分别对平动轴和摆动轴的测量方法和辨识算法进行简要说明。
2.1 平动轴几何误差辨识
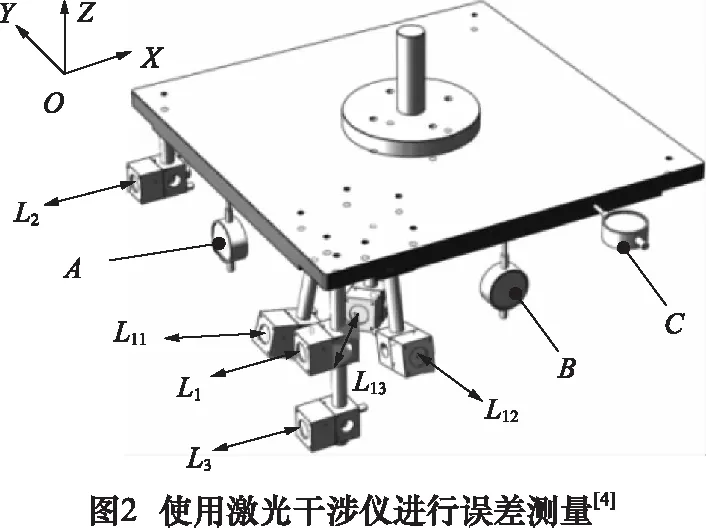
平动轴几何误差辨识以激光干涉仪为检测工具,通过辅助工装将反射镜与机床主轴固连。如图2为辅助工装三维图,双箭头L1~L13表示检测轨迹,对应轨迹上安装有激光干涉仪反射镜,辅助工装通过圆轴安装在机床主轴上[10]。根据检测策略[5]编写数控代码,驱动机床运动使反射镜沿检测轨迹移动,通过激光干涉仪检测给定轨迹上的定位误差[10]。测量所得定位误差以rtl后缀文件形式保存,如图3所示为激光干涉仪检测文件的格式。本软件将对激光干涉仪检测文件进行自动识别,将测量值取至数组中用于进行后续计算。

平动轴几何误差检测所测得定位误差实质上是机床各项几何误差综合作用的结果。为从定位误差检测结果中辨识出各项几何误差,软件采用笔者所提出的十三线辨识方法[4](检测轨迹如图4所示),以长方体空间的9条棱,3条面对角线与1条体对角线的各检测点上定位误差为数据源。通过X、Y、Z轴运动矩阵和误差传递矩阵构建刀具几何误差模型,在给定检测轨迹下得到几何误差辨识方程,并通过逐步分离和最小二乘法解算各项几何误差[5]。

2.2 转动轴几何误差辨识
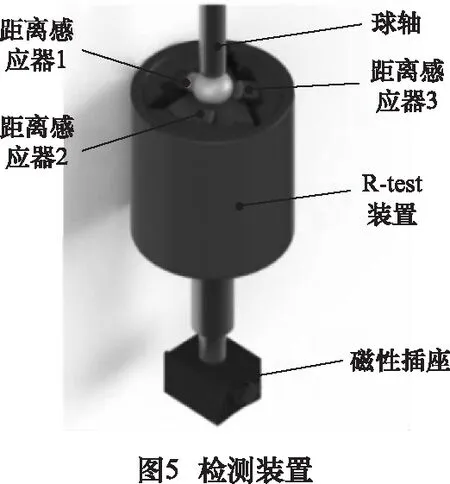
摆动轴几何误差辨识以R-test作为检测工具,通过辅助工装将带有偏置的球形检测头安装于机床主轴上[11]。基于数控机床RTCP运动功能,通过3个非接触式位移传感器检测在不同摆角时球头相对于空间理想位置的三维误差[2]。如图4所示为R-test检测示意图[6],图6所示为R-test检测所得数据的格式。在C摆动轴误差检测时,让A摆动轴静止,通过辅助工装3次改变球头相对于机床主轴的偏置参数(图6所示的水平偏置H和竖直参数L),进行RTCP运动检测得到3组数据[7]。将检测数据和A摆动轴几何误差模型[6]结合建立A摆动轴几何误差辨识模型,利用最小二乘法求解超静方程组得到A摆动轴各项几何误差[7]。在A摆动轴几何误差检测时,让C摆动轴保持静止,然后以类似的方式改变偏置参数,进行3次RTCP运动误差检测。最终将A轴的误差检测数据和几何误差模型结合,即可辨识出A轴在各个摆角下的几何误差。

3 操作流程及界面说明
根据前2章所介绍的程序架构和辨识算法,即可应用C语言在QT框架下编写补偿软件的人机交互界面。本章将对软件的误差辨识操作流程和主要界面进行介绍。
3.1 软件主界面
图7所示为软件登陆界面,输入用户名和密码点击登陆按钮即可进入软件主界面。对于不同种类的数控机床以及不同拓扑结构的进给轴,误差检测策略和辨识方法存在很大差异,数据处理方法和输出格式也有所不同。本文主要介绍龙门五轴数控机床平动轴和摆动轴几何误差辨识与补偿,其他类型机床可在后期研究工作完成后作为扩展目标添加到该软件。图8所示为龙门五轴数控机床进给轴选择界面,可以根据辨识需求进入相应界面。

3.2 平动轴检测数据导入与误差辨识
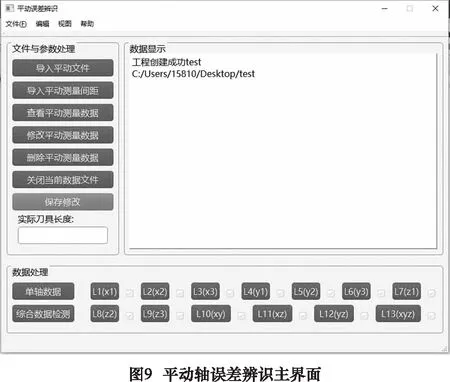
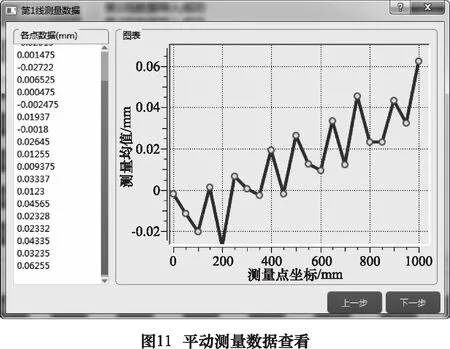
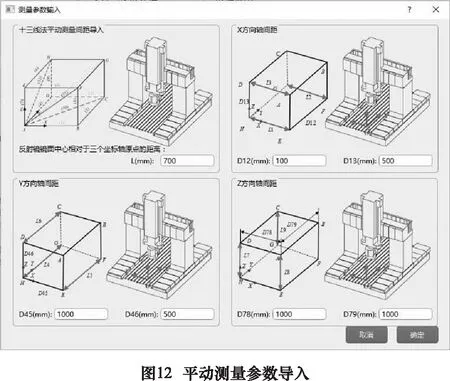
点击图8中平动轴辨识按钮,进入平动轴误差辨识主界面,如图9所示。点击界面左上角文件按钮,选择新建文件或者打开文件后,可新建辨识工程或打开已有辨识工程进行操作。平动轴几何误差辨识程序是基于13线法开发的,点击“导入平动文件”按钮可将13组测量数据分别导入辨识程序,导入界面如图10所示。已经导入的数据会在对应线号旁以绿钩形式提示,点击线号按钮可查看已经导入的各组数据,数据查看界面如图11所示。如果有存在疑问的数据可以删除后重新导入或对局部数据进行修正。完成检测数据导入后,点击“导入平动测量间距”按钮输入测量工装的参数(图12),即可为误差辨识提供计算参数。
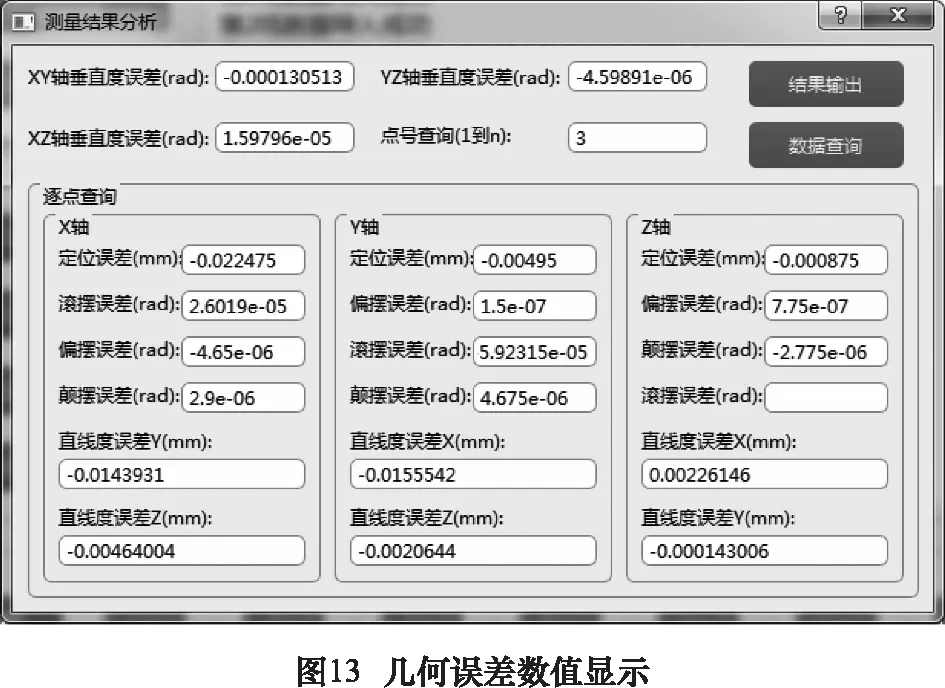
在测量数据和测量参数都导入之后,点击主界面(图9)的“综合数据检测”按钮即可在新的窗口中查看误差辨识结果,如图13为几何误差辨识结果显示界面。输入查询点号后点击数据查询按钮,窗体下方即显示X、Y、Z三轴上相应点的各项误差值。点击“结果输出按钮”可在新的窗口中对误差补偿输出值进行定义和修正。根据实际误差检测情况定义检测零点在机床坐标系下的坐标值,从而确定补偿列表生成的起始点。在补偿修正系数窗口更改各项补偿值的修正倍率(初始为1),有助于实现迭代补偿,提升补偿效果。在补偿修正系数和检测坐标确定之后,点击“保存并绘图”按钮即可将补偿数据以图形展示(如图14所示)。点击“输出至文件”按钮,补偿文件会自动生成至初始创建工程的文件夹中,该补偿文件形式如图15所示,可以直接导入数控系统实现平动轴几何误差自动补偿。


3.3 摆动轴检测数据导入与误差辨识
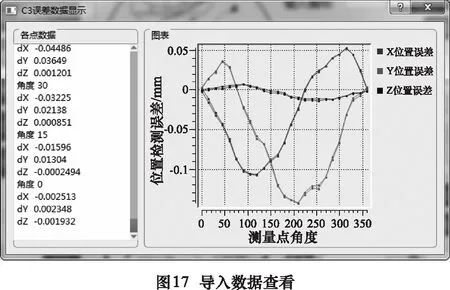
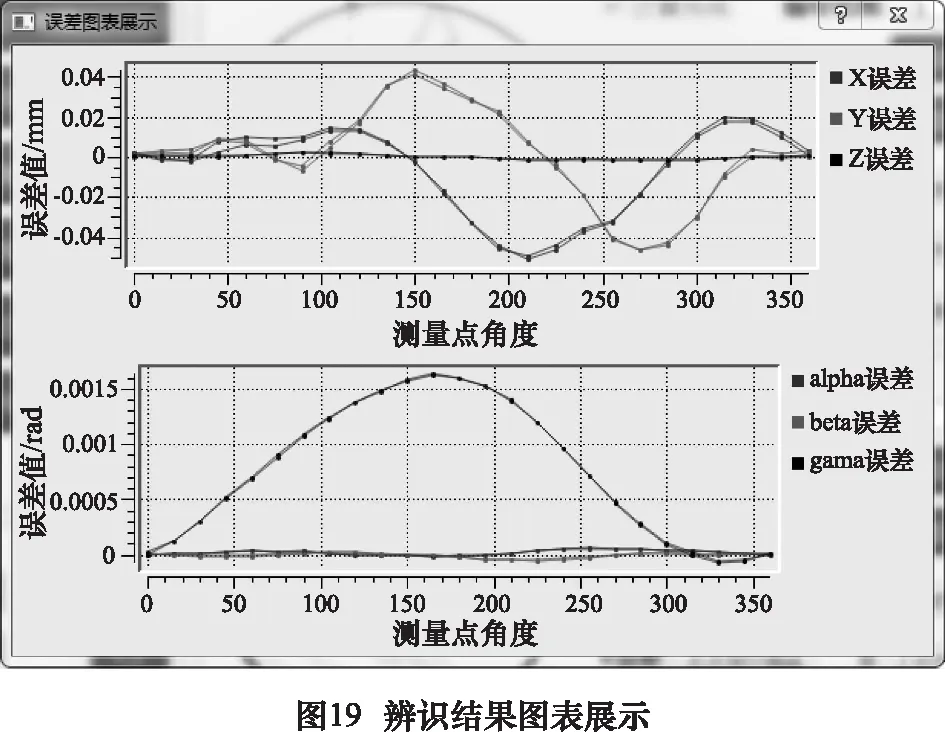
在进给轴选择界面(图8所示)选择“转动轴辨识”进入转动轴辨识程序。点击界面左上角文件按钮,选择新建文件或者打开文件后,即可在打开工程中进行后续操作。基于转动轴几何误差检测策略[7],在转动轴误差辨识主界面(如图16所示)的引导下,分别将A、C摆动轴所对应的3组数据导入软件。已经导入的数据会在下方以绿钩加以提示,可点击相应按钮查看已经导入的各组数据(如图17所示),如果有存在疑问的数据可以删除后重新导入或对局部数据进行修正。接着可以在“计算参数导入”下输入工装的偏置参数,具体输入形式与图12所示平动测量参数导入类似。A摆动轴和C摆动轴的辨识算法互相独立,故点击左侧的“A/C摆动轴误差分析”可以分别获得其误差辨识结果。计算完成后,右侧“计算完成”按钮旁会显示绿钩,输入查询编号后点击“结果查询按钮”即可查看相应角度的各项误差(如图18所示)。当摆动轴误差计算完成后,点击相应图表展示按钮,即可在新窗口中以曲线图的形式查看辨识结果(如图19所示)。

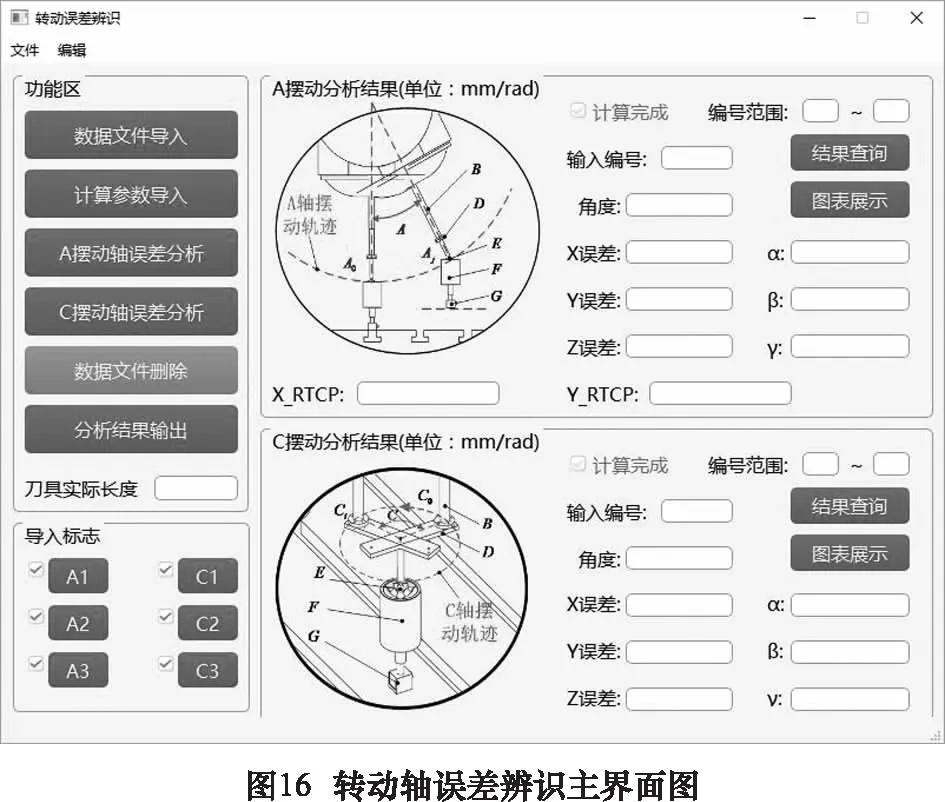
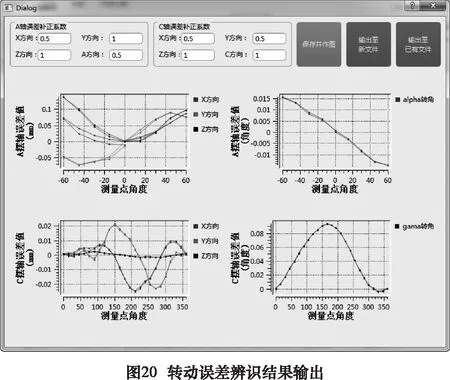
在完成摆动轴几何误差辨识计算后,点击主界面上的“分析结果输出”按钮,在弹出窗口中输入各个补偿值的修正系数,点击“保存并作图”即可图形化显示补偿数据的基本情况,如图20所示。在图20中核对数据无误后,点击输出至新文件即可在工程文件夹中生成补偿文件(该数据只补偿了摆动轴),或者点击输出至已有文件后选择平动轴辨识中生成的补偿文件,转动轴的补偿值会被追加在平动轴补偿文件的末尾(该数据对平动轴和摆动轴同时进行了补偿)。

4 软件补偿效果验证
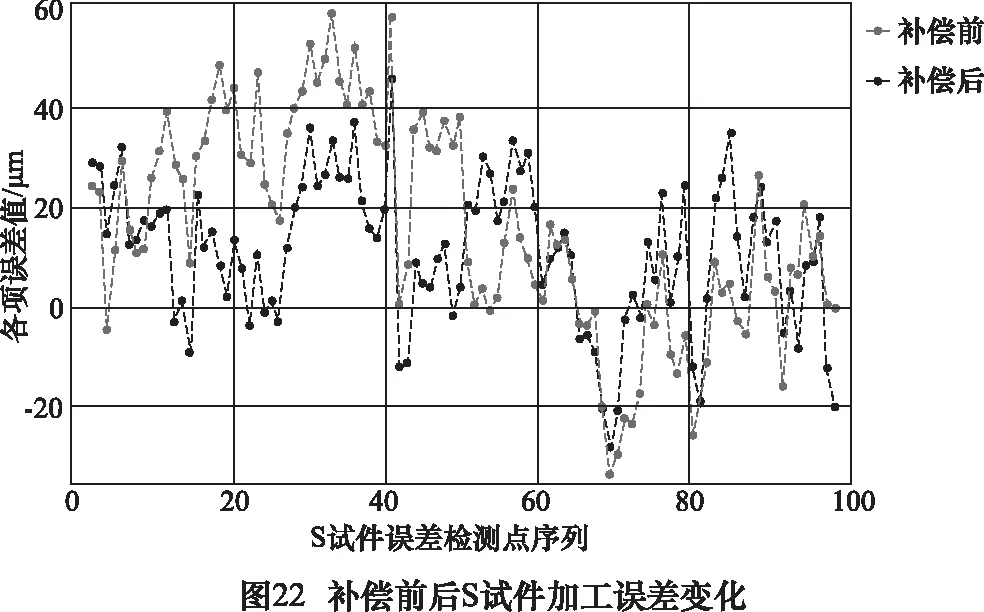
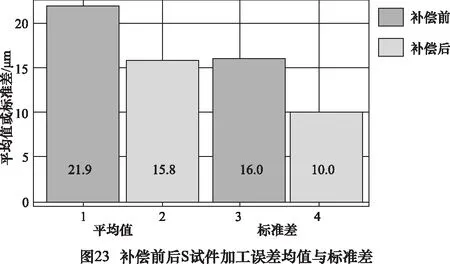
为验证几何误差补偿软件的实用性,如图21所示,在一台龙门五轴数控机床上进行了 S试件切削实验。采用对比补偿前后机床切削S试件的加工精度对机床的加工精度进行了评估和比较。为了反映加工误差的大小,在S试件曲面上选择了100个特征点,分别测量其在曲面法向上的加工误差值。在无误差补偿的情况下进行一次S试件加工与误差测量,然后基于误差检测数据利用误差补偿软件导入误差补偿文件再进行一次加工。将两次试件的加工误差进行对比,误差补偿前后加工误差的变化如图22所示,补偿前后S试件加工误差平均值与方差如图23所示。

由图22可知,S试件100项检测误差中补偿前最大值为59.7 μm补偿后最大值减小至46.3 μm,最大误差改善效果达到了22.4%。同时由图23可知,补偿后100项误差均值从21.9 μm减小至16 μm,平均改善效果改善了26.9%,标准差从15.8 μm减小至10 μm,加工精度稳定性提升了36.7%。由此说明,采用该软件对机床几何误差进行补偿后,机床的加工精度和加工稳定性都有较为明显的提升。
5 结语
本文以具有西门子840D数控系统的龙门五轴数控机床为应用对象,基于十三线平动轴几何误差辨识方法和偏置球心R-test的摆动轴几何误差辨识方法,在C++环境下利用QT界面设计框架,开发了一种几何误差补偿软件。软件在导入激光干涉仪和R-test误差测量数据后,可以快速辨识出机床各项几何误差,并输出能被西门子数控系统识别的补偿文件,通过数控系统加载补偿文件便可以实现几何误差的自动化补偿,有效地提升了数控机床几何误差补偿的效率。通过切削S试件对软件误差应用效果进行了验证,结果表明应用该软件进行误差补偿可以有效提升机床在加工精度和加工稳定性。本文所开发的误差补偿软件可以快速、高效地实现龙门五轴数控机床几何误差的补偿,为机床航空结构件加工精度的保证提供了有力支持。此外值得指出,以现有单机版本软件为基础,在辨识算法优化、人机交互、操作便捷性方面继续深入挖掘,基于网络架构开发出更为通用的误差补偿软件,在航空结构件加工领域乃至整个机械加工领域都有重大的应用前景。
[1]李杰, 刘辛军, 谢福贵,等. 基于时变特性的数控机床综合误差建模方法[J]. 科技导报, 2016, 34(2):65-70.
[2]李杰, 谢福贵, 刘辛军,等. 五轴数控机床空间定位精度改善方法研究现状分析[J]. 机械工程学报,2017,53(7):113-128.
[3]Li J, Xie F, Liu X J. Geometric error modeling and sensitivity analysis of a five-axis machine tool[J]. The International Journal of Advanced Manufacturing Technology, 2016, 82(9):2037-2051.
[4]Li J, Xie F, Liu X J, et al. Geometric error identification and compensation of linear axes based on a novel 13-line method[J]. International Journal of Advanced Manufacturing Technology, 2016, 87(5-8): 2269-2283.
[5]刘辛军, 李杰, 董泽园,等. 机床平动轴几何误差辨识方法, CN105538038A[P]. 2016.
[6]Li J, Xie F, Liu X J, et al. A geometric error identification method for the swiveling axes of five-axis machine tools by static R-test[J]. International Journal of Advanced Manufacturing Technology, 2017, 89(9):3393-3405.
[7]刘辛军, 李杰, 陈俊宇,等. 基于RTCP的五轴数控机床摆动轴几何误差辨识方法, CN105479268A[P]. 2016.
[8]Dave Maxham.空间误差补偿技术在大型多轴机床标定中的实用方法[J]. 航空制造技术, 2010(13):46-49.
[9]周汉辉. 数控机床三维几何误差补偿技术的应用[J]. 航空制造技术, 2011(6):40-43.
[10]刘辛军, 李杰, 朱绍维,等. 一种激光干涉仪辅助组合夹具, CN104729401A[P]. 2015-06-24.
[11]刘辛军, 李杰, 董泽园. 用于双摆头五轴数控机床R-test检测的辅助工装, CN 106041643A[P]. 2016
[12]Qt, Nokia Corporation. QtCross-platform application and UI framework, 4.8.2[EB/OL]. 2012.
[13]Uwe Rathmann Josef Wilgen. Qwt User's Guide[M].2008
[14]Rathmann, U, Wilgen, J. Qwt-Qt Widgets for Technical Applications, 6.0.1[EB/OL].2012.
[15]卢华伟, 秦品健, 郑锐. 基于Qt/Qwt的操作监控系统的设计与实现[J]. 微计算机信息, 2010, 26(1):72-74.
[16]霍亚飞. Qt Creator快速入门[M].北京:北京航空航天大学出版社, 2014.

