例谈新课标下中考“新定义”

仇建新

(江苏省海门市能仁中学 226100)

一、类型

初中数学“新定义”试题“先学习理解，后运(应)用”.从题型来看，有展示全貌，留空补缺的；有说明解题缘由的；有要求总结规律再解决问题的；有理解新定义(概念)再解决问题的，等等.此类试题虽不来源于初中课本却高于课本，结构独特，大致可分四类：

1.纯文型——全部用文字表述条件和问题(结论)

2.图文型——用图形和文字综合表述条件和问题(结论)

3.表文型——用表格和文字综合表述条件和问题(结论)

4.其它型——条件、问题、解题过程都已展示的前提下，考查“新定义”阅读材料的分析与解决应用问题等能力，此类题型特点鲜明.

二、步骤

无论以上何种类型，解决“新定义”试题，在读题、译题、建模解模、答题等思维过程中，其解答步骤大致分以下几步：

1.快速浏览，抓重点——明确主旨

在阅读时不仅要特别留意“新定义”描述的情景、相关数据、关键词句等细节，还要注意问题的呈现方式.据此揣摩命题人意图，思考是我们平常练习时的何种类型？涉及哪些知识方法？一般是如何解决的？在头脑中建立初步印记，明确主旨，第一步很重要.

2.专心阅读，提要点——提炼信息

再次阅读不仅要注意各个关键数据(勾、圈、画标识)，还要注意各数据的潜在关联，尤其是一些特殊条件(隐含条件挖掘)，以简明扼要地找出各量的关系，提炼信息，把握要点，要牢记尊重原题中的信息.

3.融合信息，剖难点——构建数模

根据前面提炼的信息分析、加工材料中关键词、句，选用恰当、合理的数学模型，例如由“大于、不超过、至少…”等联想到建立不等式(组)；由“等于…，恰好…”联想到建立方程(组)；由“求哪种方案更节省、或求出…和…的函数关系式或求最大值(最小值)”等联想到建立函数模型，将题中的各种已知量用数学符号语言准确地表达其内在联系.

4.解决数模，溯原点——反思检查

在建立好相应的数学模型后，不要急于解决问题，而应回过头来重新审题，一是检查哪些数据、关系可能遗漏，用得是否准确，要充分利用题中显条件并善于挖掘题中隐含条件；二是关键词、句的理解是否准确、到位；三是判断所列关系式的量是否符合实际意义；四是在解题过程中要善于反思检查，发现问题及时修正.

三、例举历年中考“新定义”试题具体谈一谈

例1 (2017年江苏南通27题)我们知道，三角形的内心是三条角平分线的交点.过三角形内心的一条直线与两边相交，两交点之间的线段把这个三角形分成两个图形，若有一个图形与原三角形相似，则把这条线段叫做这个三角形的“内似线”.

(1)等边三角形“内似线”的条数为____；

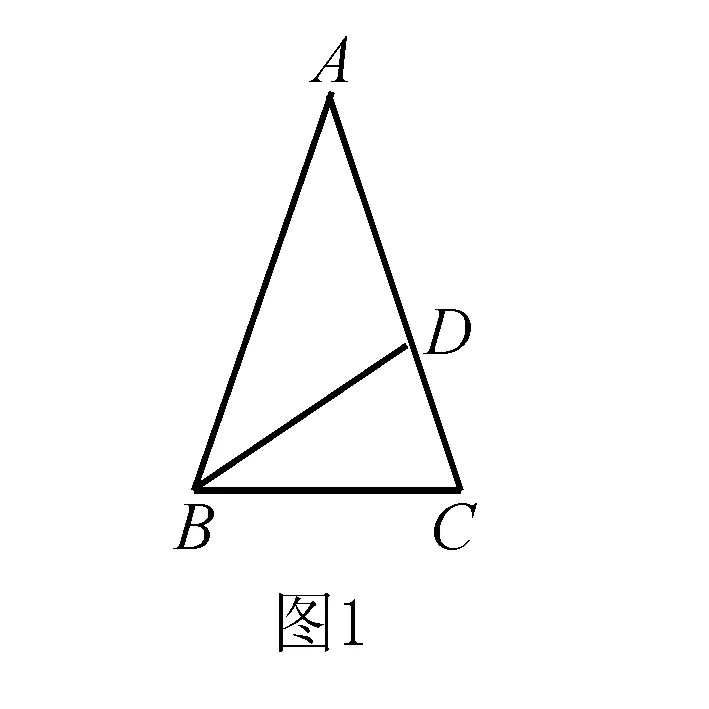
(2)如图1，△ABC中，AB=AC，点D在AC上，且BD=BC=AD,求证：BD是△ABC的“内似线”；

(3)在Rt△ABC中，∠C=90°，AC=4，BC=3，E，F分别在边AC，BC上，且EF是△ABC的“内似线”，求EF的长.

考点剖析考查相似三角形的判定与性质，等腰三角形的性质，三角形内心性质，三角形面积公式等知识.渗透由特殊与一般思想、分类讨论思想、转化思想等，难度中等偏上.

思路评析本例题属于“图文型”阅读理解，由新定义“内似线”(条件)引发三个问题，综合考查初中阶段与三角形有关知识，读懂并理解“内似线”定义是解题的关键.(1)问根据“内似线”定义解决等边三角形应用，难度不大；(2)问联想到平时训练的“黄金三角形”，考生若从这个“基本图形”突破即可解答；(3)问又是一种特殊三角形(直角三角形)，考查知识比较全面，通过“内心”添加常见辅助线，相似三角形的分类，基本运算等，此问考生可能遗漏情形，有一定难度.

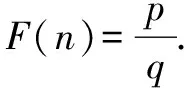
(1) 如果一个正整数a是另外一个正整数b的平方，我们称正整数a是完全平方数.求证：对任意一个完全平方数m，总有F(m)=1.

(2) 如果一个两位正整数t，t=10x+y(1≤x≤y≤9，x、y为自然数)，交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18，那么我们称这个数t为“吉祥数”，求所有“吉祥数”中F(t)的最大值.

考查完全平方数的分解，两位数的正确表达，熟练计算，构建函数模型以及会解不定方程，渗透分类思想、函数思想等.本题“新定义”下读懂“最佳分解”(规定)与“吉祥数”的意义是解题关键，属于中档题.

思路评析本例题属于“纯文型”阅读理解题，审清题意，理解新定义最佳分解及“吉祥数”的意义(条件)是关键.(1)任意一个完全平方数均可写成两个相同的正整数的积，这两个正整数的差是0，其差的绝对值最小，根据最佳分解的“规定”可知对于任意一个完全平方数m，总有F(m)=1；(2)①用含x，y的代数式正确表达两位正整数，②根据“新的两位正整数-原两位正整数=18”(条件)可确定y与x之间的函数关系式(建立函数模型)；③由1≤x≤y≤9，x、y为自然数，分类、讨论求出所有符合的“吉祥数”，④根据最佳分解的“规定”即可求出每个“吉祥数”的最佳分解结果，通过计算比较大小即可得到(问题)结论.

参考文献：

[1]康世刚，宋乃庆.论数学素养的内涵及特征[J].数学通报,2015(03).

[2]吴怡.浅谈学生数学素养的提高[J].理科考试研究,2017(14).