An Optimized Labeling Scheme for Reachability Queries
Xian Tang , Ziyang Chen, Haiyan Zhang, Xiang Liu Yunyu Shi and Asad Shahzadi
1 Introduction
A reachability queryu?→vasks, in a directed graphG, whether there exists a path fromutov. Answering reachability queries is one of the fundamental graph operations, which has been extensively studied in the past decades [Agrawal, Borgida and Jagadish (1989); Chen,Gupta and Kurul (2005); Chen and Chen (2008); Chen and Chen (2011); Cheng, Huang,Wu et al. (2013); Cheng, Yu, Lin et al. (2006); Cheng, Yu, Lin et al. (2008); Cohen,Halperin, Kaplan et al. (2002); Jagadish (1990); Jin, Ruan, Dey et al. (2012); Jin, Ruan,Xiang et al. (2011); Jin and Wang (2013); Jin, Xiang, Ruan et al. (2009); Jin, Xiang, Ruan et al. (2008); Seufert, Anand, Bedathur et al. (2013); Su, Zhu, Wei et al. (2017); Triß l and Leser (2007); van Schaik and de Moor (2011); Veloso, Cerf, Junior et al. (2014); Wang,
He, Yang et al. (2006); Wei, Yu, Lu et al. (2014); Yano, Akiba, Iwata et al. (2013); Yildirim,Chaoji and Zaki (2010); Yildirim, Chaoji and Zaki (2012); Yu and Cheng (2010); Zhang,Yu, Qin et al. (2012); Zhu, Lin, Wang et al. (2014); Li and Li (2010)]. Its applications include, but not limited to, Semantic Web (RDF), online social networks, biological networks, ontology, transportation networks, etc. For reachability queries processing, there are three interrelated issues: Index size, index construction time, and query time. Given a reachability queryu?→v, the two extremes of answering it are: (1) traversing fromutovto find the final answer without building index in-advance, and (2) maintaining the whole transitive closure (TC) to check whetherucan reachv. On one hand, the traversing approaches do not need to build index offline, however, it needs to visit all nodes thatucan reach in the worst case by performing expensive depth-first-search (DFS) or breadthfirst-search (BFS) operation to answer the given query. On the other hand, computing theTCmakes it difficult to be scaled to large graphs, due to unacceptable index size and indexing time. Considering this problem, all existing approaches made trade-off among index construction, index size and query performance, where index construction is a onetime activity. Due to its importance and the emergence of large graphs in big data era [Wu,Zapevalova, Chen et al. (2018)], faster answering reachability queriesonlineis still a challenging task, supposing that the index can be constructedofflinewith reasonable time and size.
We follow [Wei, Yu, Lu et al. (2014)] and classify existing methods into two categories according to the coverage of index on reachability information:Label-Only[Agrawal,Borgida and Jagadish (1989); Chen and Chen (2008); Cheng, Huang, Wu et al. (2013);Cohen, Halperin, Kaplan et al. (2002); Jagadish (1990); Jin and Wang (2013); Jin, Xiang,Ruan et al. (2009); Jin, Xiang, Ruan et al. (2008); van Schaik and de Moor (2011); Wang,He, Yang et al. (2006); Yano, Akiba, Iwata et al. (2013); Zhu, Lin, Wang et al. (2014)] andLabel+G[Chen, Gupta and Kurul (2005); Jin, Ruan, Dey et al. (2012); Jin and Wang(2013); Seufert, Anand, Bedathur et al. (2013); Triß l and Leser (2007); Veloso, Cerf, Junior et al. (2014); Wei, Yu, Lu et al. (2014; Yano, Akiba, Iwata et al. (2013); Yildirim, Chaoji and Zaki (2010); Yildirim, Chaoji and Zaki (2012)]. Here, we say an algorithm belongs toLabel-Only, it means that the index conveys thecompletereachability information, and any given queryu?→vcan be answered by comparing labels ofuandv. When we say that an algorithm belongs toLabel+G, it means that the index coverspartialreachability information, thus we may need to performDFS/BFSfromuto check whetherucan reachv, if we cannot get the result by comparing labels ofuandv. Most existingLabel+Gapproaches possess the benefits of bounded index size and index construction time in theory. However, they all suffer from the same performance bottleneck, i.e. traversing fromutovto find the answer. As a comparison, among existingLabel-Onlyapproaches, recent variants of 2-hop labels, such asPLL[Yano, Akiba, Iwataet al. (2013)],DL[Jin and Wang(2013)],TF[Cheng, Huang, Wu et al. (2013)] andTOL[Zhu, Lin, Wang et al. (2014)],does not suffer from the expensiveDFS/BFSoperation on the underlying graph. Moreover,the index can be constructed efficiently with reasonable size, which makes these approaches can scale to large graphs. However, they could beinefficientwhen answeringunreachablequeries due to the higher cost of set intersection operation on node labels to get the result.
To overcome the shorting comings of existing approaches, we propose a novelLabel-Onlylabeling scheme, namelyT2H, based on which reachability queries can be answered more efficiently than current ones. Given aDAG G, the basic idea is finding fromGa set of“block nodes”, such that after removing these block nodes fromG, we get a reduced graphG1, and the reachability relationship between any pair of nodes inG1can be answered in constant time with linear index size. Then, for reachability relationship conveyed by block nodes, we construct block nodes based 2-hop labels to reduce the 2-hop index size. The benefits of our labeling scheme lie in the following aspects: (1) compared with existingLabel+Gapproaches, our method does not need to perform costlyDFS/BFSoperation, and can be much more efficient than existing ones when answering reachable queries, (2)compared with existingLabel-Onlyapproaches, our method significantly reduces the cost of set intersection operation on node labels to get final results. We conduct rich experiment on real datasets to show that our approach can answer both positive and negative queries very efficiently, and can scale to large graphs.
2 Background and related work
We follow the tradition of existing approaches and assume that the input graph is aDAG G=(V,E), which can be constructed from the given directed graph G in linear time w.r.t.the size of G [Tarjan (1972)] by coalescing eachSCCof G into a node inG, where each nodev∈Vrepresents anSCC Svof G, and each edge (u,v)∈Erepresents the edge fromSCC SutoSvif there is an edge from a node inSuto a node inSv. Similar as Zhou et [Zhou, Zhou,Yu et al. (2017)], we useinG(u)={v|(u,v)∈E} to denote the al. set of in-neighbors nodes ofuinG, andoutG(u)={v|(u,v)∈E} the set of out-neighbors nodes ofu. We use(u) to denote the set of nodes inGthat can reachuwhereu∉(u), andthe set of nodes inGthatucan reach whereu∉(u). We useX={1, 2, …, |V|} to denote a topological order (topo-order) ofG, which can be got by performing a topological sorting onGin linear timeO(|V|+|E|) [Simon (1988)]. A topological sorting ofGis a mappingtX: V→X, such that ∀(u,v)∈E, we have<, where() is the topo-order ofu(v) w.r.t. X.
We discuss existing algorithms from two categories: (1)Label-Onlyand (2)Label+G. ByLabel-Only, a given queryu?→vcan be answered by comparing labels ofuandv. ByLabel+G, this query can be answered byDFS/BFSat run-time, when it cannot be answered by labels ofuandv. We useu→v(u↛v) to denote thatucan (cannot) reachv.
TheLabel-Onlymethods [Agrawal, Borgida and Jagadish (1989); Cheng, Huang, Wu et al.(2013); Jin, Ruan, Xiang et al. (2011); Jin and Wang (2013); Jin, Xiang, Ruan et al. (2009);Jin, Xiang, Ruan et al. (2008); van Schaik and de Moor (2011); Yano, Akiba, Iwata et al.(2013); Zhu, Lin, Wang et al. (2014)] focus on compressingTCto get a smaller index size for fast query processing. The recent work includes variants of 2-hop labeling scheme, such asTF[Cheng, Huang, Wu et al. (2013)],DL[Jin and Wang (2013)],PLL[Yano, Akiba,Iwata et al. (2013)] andTOL[Zhu, Lin, Wang et al. (2014)]. The idea is to assign each nodeua labelLu={Lout(u),Lin(u)}, whereLout(u)(Lin(u)) is called the out (in) label ofuconsisting of a set of nodes that u can reach (be reached). Based on this labeling scheme,u?→vcan be answered by testing whether the result ofLout(u)∩Lin(v) is empty or not. IfLout(u)∩Lin(v)≠ ∅, thenu→v, otherwiseu↛v. To compute node labels,TF[Cheng, Huang,Wu et al. (2013)] folds the givenDAGrecursively based on topological level to reduce the cost of 2-hop computation.DL[Jin and Wang (2013)],PLL[Yano, Akiba, Iwata et al.(2013)] andTOL[Zhu, Lin, Wang et al. (2014)] share the similar idea of computing 2-hop labels. Given all nodes in a certain order, the construction ofDLandPLLlabels is enumerating each node with a forwardBFSand a backwardBFSto add u to labels of nodes thatucan reach and nodes that can reachu. During eachBFS, an early stop condition is adopted to accelerate the computation and reduce the index size.
TheLabel+Gmethods [Seufert, Anand, Bedathur et al. (2013); Triß l and Leser (2007);Veloso, Cerf, Junior et al. (2014); Wei, Yu, Lu et al. (2014); Yildirim, Chaoji and Zaki(2010); Yildirim, Chaoji and Zaki (2012)] answeru?→vby performingDFSfromuat runtime if needed. The recent work includesGRAIL[Yildirim, Chaoji and Zaki (2010);Yildirim, Chaoji and Zaki (2012)],FERRARI[Seufert, Anand, Bedathur et al. (2013)],FELINE[Veloso, Cerf, Junior et al. (2014)] andIP+[Wei, Yu, Lu et al. (2014)]. All these methods focus on efficient pruning techniques to answer most unreachable queries. They also use additional pruning strategies to make optimization on both positive and negative queries, such as comparing topological levels [Seufert, Anand, Bedathur et al. (2013);Veloso, Cerf, Junior et al. (2014); Wei, Yu, Lu et al. (2014); Yildirim, Chaoji and Zaki(2010); Yildirim, Chaoji and Zaki (2012)], comparing topological orders [Seufert, Anand,Bedathur et al. (2013)], and comparing intervals ofuandvover a spanning tree [Veloso,Cerf, Junior et al. (2014)].
Apart from the above methods that work on a largeDAG G, there are studies focusing on reducingGto a smallerDAGto accelerate reachability query processing, includingSCARABFramework [Jin, Ruan, Dey et al. (2012)] and equivalence reduction [Fan, Li,Wang et al. (2012); Zhou, Zhou, Yu et al. (2017)], which are orthogonal to the above approaches and can be combined with the above approaches to accelerate answering reachability queries.
3 Query processing
3.1 The T2H labeling scheme
Given a topo-orderXof aDAG G, it is obvious that ifu→v, then we must have, but the other side does not always hold, i.e. when, we cannot conclude thatu→v.However, if for every unreachable queryu↛v, we have that, then when, we can safely say thatu→v. Therefore, the key problem is how to know that we can correctly identify all unreachable queries using topo-orders.
Given two nodesuandv, there are at most two queries, i.e.u?→vandv?→u. Therefore, it is not possible to correctly check the unreachable relationship using one topo-orders, e.g.considerv2andv3inGof Fig. 1(a), since=3>2=, we know thatv3↛v2. But, for queryv2?→v3, we cannot get the results by comparing their topo-orders. The natural idea is using one more topo-order to check the unreachable relationship on the other direction. Here, we use reversed topo-order to check unreachable queries.
Definition 1. (Free Node)During a topological sorting, a node u is called a free node, if u has not been visited, but all of u’s in-neighbors have been visited.
For example, forGin Fig. 1(a), the free node isv1before processing, and after processingv1, the free nodes arev2,v3andv5.
Definition 2. (Reversed Topo-Order)Given two topo-orders X and Y, we say X(Y) is thereversed topo-order of Y (X), if Y (X) is computed in the way that the topological sorting will always first visit and assign the topo-order in Y (X) to the free node with the maximal topo-order in X(Y).
Given the uniqueness of a topo-order, its reversed topo-order is also unique. For example,given thecircledtopo-orderXof all nodes inGof Fig. 1(a), we can get the reversed topoorderYaccording to Definition 2, as shown by the italic integer beside each node.Obviously, we know thatv3↛v2because

Figure 1: Illustration of the new labeling scheme, where (a) is a DAG with nodes denoted by their topo-orders, the italic integer beside each node is its reversed topo-order, (b) is the trivial subgraph G1 of G, the italic integer beside each node is its reversed topo-order, and(c) is the link graph G2 of G consisting of all nodes that can reach (be reached by) these block nodes
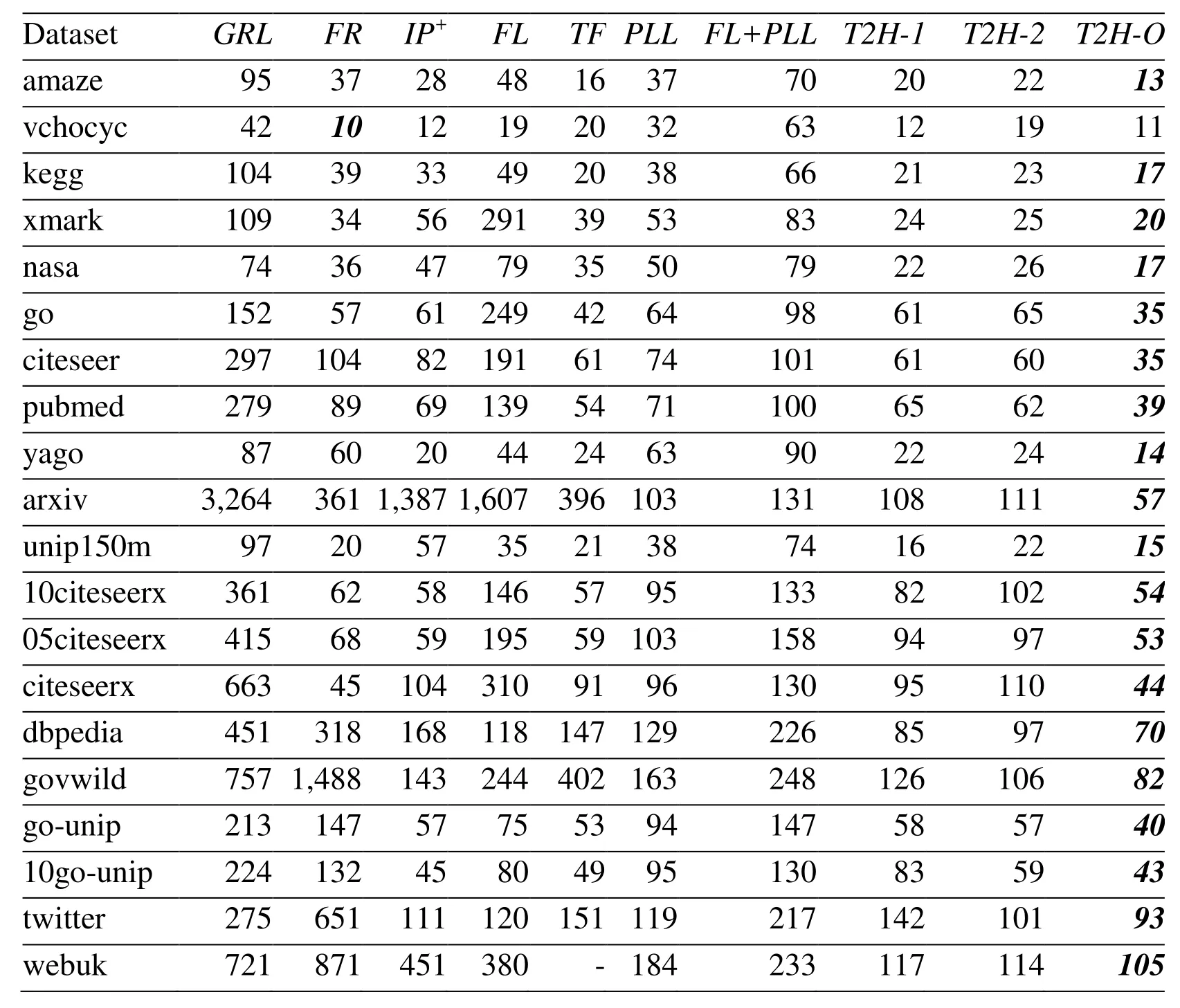
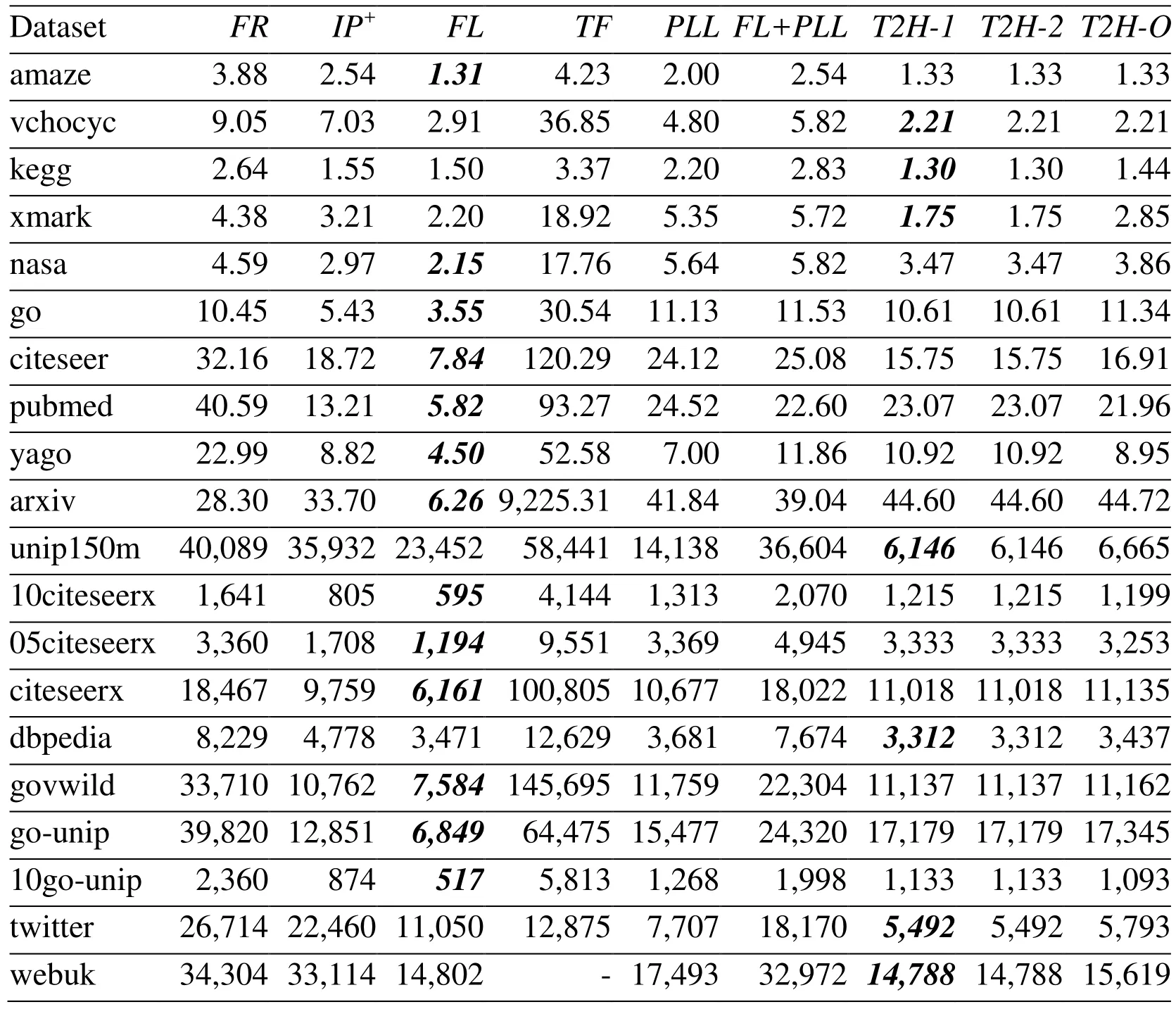
Even though we can identify more unreachable queries using multiple topo-orders, there exists some problematicDAGsfor which a limited number of topo-orders will always produce false positive answers [Kornaropoulos and Tollis (2011); Veloso, Cerf, Junior et al. (2014)], i.e. even if Definition 3. (Trivial Graph)Given a DAG G and one of its topo-order X. We say G is a trivial graph w.r.t. X, if every unreachable query on G can be identified by X and its reversed topo-order Y. For example,G1in Fig. 1(b) is a trivial graph. Interested readers can easily verify that for every unreachable query, we can always return FALSE based on the two reversed topoorders shown inG1. Definition 4. (Block Node Set)Given a DAG G, let S be a set of nodes in G. If G is a trivial graph after removing all nodes of S, then we call S a block node set of G and each node of S a block node. For example, forGin Fig. 1(a),v6is a block node, andS={v6} is a block node set ofG.After removingv6fromG, we get the trivial graphG1in Fig. 1(b).we know thatv3↛v6according toG. In Based on two above definitions, we propose to find from the givenDAG Ga trivial graphG1by removing fromGa set of “block nodes”. The basic idea is that given a trivial graphG1, we can identify all unreachable queries based on two reversed topo-orders. Then, for the reachability relationship between nodes inGthat cannot be covered by the two topoorders, we construct 2-hop labels from these block nodes. For example, forGin Fig. 1(a),we generate the trivial graphG1in Fig. 1(b) by removing the unique block nodev6. To answer reachability queries, we assign each node inG1two topo-orders shown in Fig. 1(b).Then, we performing forward and backwardDFS/BFSfromv6to construct 2-hop labels.Combining the two aspects together, we have theT2H(short for topo-order and 2-hop)label for each node, which we call as theT2Hlabeling scheme. Hereafter, we usetvto denote bothand.We call it asv’s topo-label, andtu Before discussing the query algorithm, lets first introduce the following results. Theorem 1.Given a trivial graph G1, we can answer all queries between nodes in G1using two reversed topo-orders. Proof. First, we can answer all unreachable queries using two reversed topo-orders according to Definition 3. Assume that there exists a reachable queryu→vthat we cannot correctly answer, it means that we havetu≮tv. Then, we know thatu↛v, which contradicts the assumption. Therefore, we can answer all queries using two reversed topo-orders. Definition 5.Given a DAG G and the set of block nodes S, we call the graph consists of all nodes that can reach and be reached by every block node the link graph w.r.t. S. For example, forGin Fig. 1(a),v6is its unique block node, and the link graph is shown asG2in Fig. 1(c). We have the following result. Corollary 1.Given a DAG G=(V, E), its trivial graph G1=(V1,E1) and link graph G2=(V2,E2), we have that V=V1∪V2and E=E1∪E2. Theorem 2.All queries can be correctly answered based on T2H labels. Proof.First, according to Theorem 1, we can answer all reachable queries between nodes inG1. Second, the remaining queries overGcan be either reachable through block nodes, or unreachable. Thus, by comparing block nodes based 2-hop labels, we can correctly answer the remaining reachable queries, and all other queries are definitely unreachable ones. Based on Theorems 1 and 2, we have Algorithm 1, which first check whether u can reachvusing topo-labels in lines 1-2, then check whetherucan reachvusing block nodes based 2-hop labels in lines 2-3. And return FALSE in line 5 to denote thatucannot reachv. Example 1. ConsiderGin Fig. 1(a). TheT2Hlabels are shown in Figs. 1(b) and 1(c). For queryv3?→v8, Algorithm 1 can return TRUE in line 2 denotingv3→v8due to that tv3 Obviously, if the given query can be answered in line 2, then the time complexity isO(1),otherwise, the time complexity isO(L), whereLis maximal length of block nodes based 2-hop labels. Further, as block nodes based 2-hop labels capture all reachable relationships between nodes linked by them, we have the second algorithm to answer a given query, as shown by Algorithm 2. The correctness is based on Theorems 1 and 2. The difference between the two algorithms lies in whether we first compare topo-labels. And the time complexity of Algorithm 2 isO(L). In essence, either algorithm can work better than the other in different scenario. If most reachable queries cannot be answered by comparing topo-labels, then Algorithm 2 could be more efficient, otherwise Algorithm 1 could be better. Both Algorithms 1 and 2 involve two operations when answering reachability queries, i.e.comparing topo-labels and comparing block nodes based 2-hop labels. As the cost of comparing topo-labels isO(1), which is better than that of comparing 2-hop labels with costO(L), if most reachable queries can be answered by comparing topo-labels, then Algorithm 1 is the better choice. Unfortunately, this is not true in practice, especially for randomly generated workload, where most queries are unreachable ones. The optimization in this section is to extend the topo-labels, such that it can be used in Algorithm 1 to test not only reachable queries, but also unreachable queries. The idea is to assignGone more topo-orderZ, which is the reversed topo-order ofX. In summary, in the optimized algorithm, there are three topo-ordersX,Y,Z, whereXandYare mutually reversed to each other w.r.t. the trivial graphG1, while X and Z are mutually reversed to each other w.r.t. the input graphG. Since the given reachability queries are answered according toG, and an unreachable query onG1could be reachable onG, thusXandYcannot be used to find unreachable queries before comparing block nodes based 2-hop labels. Fortunately, we can useXandZto find unreachable queries, which are defined onG. In this way, we can answer more queries in constant time. Based on the above discussion, we have the optimized algorithm with the same time complexity as Algorithm 1, as shown below. We first discuss how to generate the block nodes based 2-hop labels. Given a set of block nodes, we perform forward (backward)BFSfrom each block node to add it to the in (out)label of the set of nodes that it can reach (be reached by). This is similar to existing 2-hop approaches [Jin and Wang (2013); Yano, Akiba, Iwata et al. (2013); Zhu, Lin, Wang et al.(2014)]. The difference is that the number of nodes from which we performBFSis reduced.We then discuss how to generate topo-labels and block nodes. GivenG, we perform the first topological sorting onGto generate topo-orderX. This can be done by performing the following steps: (1) push all free nodes into a stackS, (2) pop a nodeufromS, assignuits topo-order, and push all ofu’s out-neighbors which are new free nodes intoS, and (3)repeat the above two steps untilSis empty. For example, every node u in Fig. 1(a) is denoted by its topo-order. GivenX, we discuss how to generateZ. Similar as generatingX, we generateZby the following steps: (1) push all free nodes into a stackSin ascending order w.r.t.X, such that they are popped out fromSin descending order, (2) pop a nodeufromS, assignuits topoorder, and push all of u’s out-neighbors which are new free nodes intoSin ascending order w.r.t.X, and (3) repeat the above two steps untilSis empty, e.g. the reversed topo-orderfor each nodeuin Fig. 1(a) is denoted by the italic integers besideu. Finally, we discuss how to find block nodes and generate the reversed topo-orderYw.r.t.the trivial graphG1. Here, we do not need to first find block nodes to actually generate the trivial graphG1. Instead, we do both when computing the reversed topo-orderY. Definition 6. (Candidate Free Node (CFN))When performing topological sorting to compute Y according to X, we say a node v is a candidate free node (CFN), if v it is not a free node and at least one of its in-neighbors u has been assigned a topo-order. For example, when computingYbased onXforGin Fig. 1(a), after visitingv1, we know thatv2,v3andv5are new free nodes. They are pushed into stackSin theirXtopo-order.Thus the next processed node isv5. After processingv5,v6is a CFN according to Definition 6. Now, we can formally give out the definition of block node, as show below. Definition 7. (Block Node (BN))When computing Y according to X, let w be the largest unprocessed in-neighbor of v w.r.t. X, and u the currently being processed free node, we say node v is a block node (BN), if v it is a CFN and<. Intuitively, for currently being processed nodeu, when we say thatvis a block node, it means thatucannot reachv, and if we assignuits, then we have that, and based on which we cannot say thatu→vholds. That is,vprevents us from checking all reachability relationship by two topo-orders. Therefore, to avoid the costly traversing operation when answering reachability queries, while at the same time reduce the cost of set intersection operation of existing 2-hop approaches, we computes 2-hop labels on BN only, and for other nodes, we use topo-labels to check the reachability relationship. Now, we are ready to give out the index construction algorithm, the idea is to computeYaccordingX, during which we perform forward and backwardBFSto compute 2-hop labels from each block node, as shown by Algorithm 4. The time cost of getting topo-label can be done inO(|V|+|E|). The cost of computing 2-hop labels isO(nb×|V|+|E|)., wherenbis the number of block nodes. Therefore, the time complexity of the index construction algorithm isO(nb×|V|+|E|). In our experiment, we make comparison with both existingLabel-OnlyandLabel+Galgorithms, theLabel-Onlyalgorithms includeTF[Cheng, Huang, Wu et al. (2013)],PLL[Yano, Akiba, Iwata et al. (2013)] and our algorithms. TheLabel+Galgorithms includeGRAIL[Yildirim, Chaoji and Zaki (2010); Yildirim, Chaoji and Zaki (2012)] (abbreviated asGRL),FELINE[Veloso, Cerf, Junior et al. (2014)] (abbreviated asFL) andIP+[Wei, Yu,Lu et al. (2014)]. The source codes of these existing algorithm are kindly provided by the authors. We setk=5 forGRLandIP+on all datasets. ForIP+, we seth=5 and μ=100. We implemented our algorithms using C++ and all source codes are compiled by G++6.2.0. All experiments were run on a PC with Intel(R) Xeon(R) CPU E7-4809 v3 2.00 GHz CPU,32 GB memory, and Ubuntu 16.10 Linux OS. For algorithms that run more than 24 h or exceed the memory limit (32 GB), we will show their results as “-” in the tables. Table 1: Statistics of real datasets, where d is the average degree, (∙) is the average number of reachable nodes for nodes of G, t is the number of topological levels, nb is the ratio of the number of block nodes over |V | Table 1: Statistics of real datasets, where d is the average degree, (∙) is the average number of reachable nodes for nodes of G, t is the number of topological levels, nb is the ratio of the number of block nodes over |V | Dataset |V | |E| d outG∗ (∙) t nb (%)amaze 3,710 3,600 0.97 639 16 2.91 vchocyc 9,491 10,143 1.07 14 21 2.62 kegg 3,617 3,908 1.08 729 26 3.73 xmark 6,080 7,025 1.16 57 38 2.66 nasa 5,605 6,537 1.17 19 35 9.26 go 6,793 13,361 1.97 11 16 60.19 citeseer 10,720 44,258 4.13 27 36 39.00 pubmed 9,000 40,028 4.45 31 19 41.78 yago 6,642 42,392 6.38 10 13 9.47 arxiv 6,000 66,707 11.12 821 167 66.38 unip150m 25,037,600 25,037,598 1.00 1 10 0.00 10citeseerx 770,539 1,501,126 1.95 24 36 23.46 05citeseerx 1,457,057 3,002,252 2.06 33 36 24.52 citeseerx 6,540,401 15,011,260 2.30 15,456 59 24.93 dbpedia 3,365,623 7,989,191 2.37 83,660 146 7.69 govwild 8,022,880 23,652,610 2.95 536 12 5.63 go-unip 6,967,956 34,769,339 4.99 17 21 0.25 10go-unip 469,526 3,476,397 7.40 24 21 3.50 twitter 18,121,168 18,359,487 1.01 1,346,819 22 5.76 webuk 22,753,644 38,184,039 1.68 3,417,929 2,793 4.07 Datasets:Tab. 1 shows the statistics of 20 real datasets, where the first ten are small datasets (|V|≤100,000), and the following 10 datasets are large ones (|V|>100,000). These datasets are usually used in the recent works [Cheng, Huang, Wu et al. (2013); Jin, Ruan,Dey et al. (2012); Jin and Wang (2013); Seufert, Anand, Bedathur et al. (2013); Su, Zhu,Wei et al. (2017); Veloso, Cerf, Junior et al. (2014); Wei, Yu, Lu et al. (2014); Yano, Akiba,Iwata et al. (2013); Yildirim, Chaoji and Zaki (2010); Yildirim, Chaoji and Zaki (2012);Zhu, Lin, Wang et al. (2014)], where we can find the detailed description of these datasets.Among these datasets, there are both sparse graphs (with average degreed≤2) and dense graphs (d>2). For topological levels (the 6thcolumn), Tab. 1 contains both graphs with smaller topological levels, such as unip150m, for which the topological level is 10, and graphs with very large topological levels, such as webuk with topological level as large as 2,793. For the average number of reachable nodes (the 5thcolumn), Tab. 1 also contains both graphs with nodes having few reachable nodes, such as unip150m, for which each node can reach only one node on average, and graphs with nodes having very large number of reachable nodes, such as twitter and webuk, where each node can reach 1,346,819 and 3,417,929 nodes on average, respectively. Workloads:We test these reachability algorithms using both random and equal workloads.Here, each workload contains 1,000,000 queries. The random workload is generated by sampling node pairs with the same probability on the node set of each graph. For equal workload, the “equal” means that it contains the same number of reachable and unreachable queries, i.e. it has 50% reachable queries and 50% unreachable queries. The query time is the running time of testing all queries in a workload. Note that for Tabs. 2- 5, each italic number denotes the best result in the row. From Tab. 2 we have the following observations for random workload: (1) ourT2H-Oalgorithm works best on 19 out of 20 datasets, and on the remaining one dataset,T2H-Ois also approaching the best result. The reason lies in that for reachable queries, it does not suffer from the costly traversing operation on the givenDAGasLabel+Galgorithms do,for unreachable queries, it can quickly answer most unreachable ones using topo-labels,and does not suffer from performing costly set intersection operation on 2-hop labels for most queries compared withLabel-Onlyalgorithms; (2) even thoughT2H-Oworks better thanT2H-1 andT2H-2, both the latter are very efficient compared with existing algorithms,and each one can beat the other on some datasets. This difference on query performance lies in that our method consists of comparing topo-labels and 2-hop labels, andT2H-1 andT2H-2 use different order on performing the two operations; (3) no one can beat all others on all datasets, and for existing algorithms,TFworks better than others on most datasets,but it cannot work successfully on webuk dataset. From Tab. 3 we know that for equal workload: (1) ourT2H-O algorithm works best on 16 datasets, andT2H-1 works best on three datasets, together our approaches work best on 19 datasets, and are usually much better than existingLabel-OnlyandLabel+Galgorithms;(2) for existing algorithms,Label-Onlyalgorithms usually work better thanLabel+Galgorithms, due to that for equal workload, the number of reachable queries is 50%, which can be answered more efficient usingLabel-Onlyalgorithms by avoiding costly traversing operations on the givenDAG. From both the two tables we know that simply combining existingLabel-OnlyandLabel+Gapproaches together cannot improve the overall performance. For example,FL+PLLis the combination ofFLandPLL, which is aLabel-Onlyalgorithm. We can see that in most cases, the performance ofFL+PLLis in between the other two. Even though our approach is also aLabel-Onlyalgorithm, our labeling scheme is not a simple combination ofLabel+Glabel andLabel-Onlylabel, our topo-label significantly reduces the 2-hop label size to accelerate the query performance. Table 2: Comparison of query time on random workload (ms) Table 3: Comparison of query time on equal workload (ms) Table 4: Comparison of index construction time (ms) For index construction time, we have the following observations according to Tab. 4:FL,T2H-1 andT2H-2 usually work better than others, the reasons lie in that on one hand,FLis aLabel+Galgorithm, it has the lowest time complexity, on the other hand, bothT2H-1 andT2H-2 has linear time complexity to get the topo-labels, which is used to help find block nodes. We can see from the last column of Tab. 1 that the ratio of block nodes is usually much less than the number of nodes in the given graph. Based on these block nodes,we can quickly get the 2-hop labels. Even though other existingLabel+Galgorithms have smaller time complexity on index construction, they may need more time due to traversing several times on the givenDAG. For existing algorithm,TFusually needs more time to get smallest index size and query time on several datasets, and it cannot work successfully on the webuk dataset. We can see from Tab. 5 that even thoughLabel+Galgorithms have linear index size, our approaches can achieve the best result due to reduced number of block nodes to generate 2-hop labels. And bothT2H-1 andT2H-2 achieves best results on 6 datasets. By combining the two tables together, we can see that for index construction time and index size, no one can beat all others for all datasets. And all our approaches can complete the index construction in reasonable time with acceptable index size. Based on this result,from Tab. 2 and Tab. 3 we can see that our approaches make significant improvement on query performance. In this paper, we propose a novelLabel-Onlylabeling scheme to accelerate reachability query processing. The idea comes from the fact that index construction is aone-timeactivity, while query testing is a fundamentalonlinegraph operation. Considering that existingLabel+Galgorithms are inefficient for reachable queries and existingLabel-Onlyalgorithms are inefficient for unreachable queries, we propose to use topo-labels to reduce the size of 2-hop labels to construct a newLabel-Onlylabels for fast query answering. Our experimental results show that our approaches can answer both reachable and unreachable queries more efficiently on 19 out of 20 real datasets. Acknowledgement:This work was partly supported by National Key R&D Program of China, Grant No. 2017YFB0309800, the grants from the Natural Science Foundation of China (No. 61472339, No. 61303040, No. 61572421, No. 61272124), and Shanghai Alliance Program(LM201552), and Shanghai University of Engineering and Technology School-Enterprise cooperation projects(15)(DZ-025). Agrawal, R.; Borgida, A.; Jagadish, H. V.(1989): Efficient management of transitive relationships in large data and knowledge bases.ACM SIGMOD Conference, pp. 253-262. Chen, L.; Gupta, A.; Kurul, M. E.(2005): Stack-based algorithms for pattern matching on dags.International Conference on Very Large Data Bases, pp. 493-504. Chen, Y.; Chen, Y.(2008): An efficient algorithm for answering graph reachability queries.IEEE International Conference on Data Engineering, pp. 893-902. Chen, Y.; Chen, Y.(2011): Decomposing dags into spanning trees: A new way to compress transitive closures.IEEE International Conference on Data Engineering, pp.1007-1018. Cheng, J.; Huang, S.; Wu, H.; Fu,A.(2013): Tf-label: A topological-folding labeling scheme for reachability querying in a large graph.ACM Sigmod International Conference on Management of Data, pp. 193-204. Cheng, J.; Yu, J.; Lin, X.; Wang, H.; Yu, P.(2006): Fast computation of reachability labeling for large graphs.International Conference on Advances in DatabaseTechnology,pp. 961-979. Cheng, J.; Yu, J.; Lin, X.; Wang, H.; Yu, P.(2008): Fast computing reachability labelings for large graphs with high compression rate.International Conference on Extending Database Technology, pp. 193-204. Cohen, E.; Halperin, E.; Kaplan, H.; Zwick, U.(2002): Reachability and distance queries via 2-hop labels.Symposium on Discrete Algorithms, pp. 937-946. Fan, W.; Li, J.; Wang, X.; Wu, Y.(2012): Query preserving graph compression.ACM Sigmod International Conference on Management of Data, pp. 157-168. Jagadish, H. V.(1990): A compression technique to materialize transitive closure.ACM Transactions on Database Systems, vol. 15, no. 4, pp. 558-598. Jin, R.; Ruan, N.; Dey, S.; Yu, J.(2012): SCARAB: Scaling reachability computation on large graphs.ACM Sigmod International Conference on Management of Data, pp. 169-180. Jin, R.; Ruan, N.; Xiang, Y.; Wang, H.(2011): Path-tree: An efficient reachability indexing scheme for large directed graphs.ACM Transactions on Database Systems, vol.36, no. 1, pp. 1-44. Jin, R.; Wang, G.(2013): Simple, fast, and scalable reachability oracle.Proceedings of the VVLDB Endowment, vol. 6, no. 14, pp. 1978-1989. Jin, R.; Xiang, Y.; Ruan, N.; Fuhry, D.(2009): 3-hop: A high-compression indexing scheme for reachability query.Acm Sigmod International Conference on Management of Data, pp. 813-826. Jin, R.; Xiang, Y.; Ruan, N.; Wang, H.(2008): Efficiently answering reachability queries on very large directed graphs.ACM Sigmod International Conference on Management of Data, pp. 595-608. Kornaropoulos, E. M.; Tollis, I. G.(2011): Weak dominance drawings and linear extension diameter.Data Structures and Algorithms. Li, F.; Li, G.(2010): Interval-based uncertain multi-objective optimization design of vehicle crashworthiness.Computers, Materials & Continua, vol. 15, no. 3, pp. 199-219. Seufert, S.; Anand, A.; Bedathur, S. J.; Weikum, G.(2013): FERRARI: Flexible and efficient reachability range assignment for graph indexing.IEEE International Conference on Data Engineering, pp. 1009-1020. Simon, K.(1988): An improved algorithm for transitive closure on acyclic digraphs.Theoretical Computer Science, vol. 58, no. 1, pp. 325-346. Su, J.; Zhu, Q.; Wei, H.; Yu, J.(2017): Reachability querying: Can it be even faster?IEEE Transactions on Knowledge & Data Engineer, vol. 29, no. 3, pp. 683-697. Tarjan, R. E.(1972): Depth-first search and linear graph algorithms.SIAM Journal on Computing, vol. 1, no. 2, pp. 146-160. Triß l, S.; Leser, U.(2007): Fast and practical indexing and querying of very large graphs.ACM Sigmod International Conference on Management of Data, pp. 845-856. van Schaik, S. J.; de Moor, O.(2011): A memory efficient reachability data structure through bit vector compression.ACM Sigmod International Conference on Management of Data, pp. 913-924. Veloso, R. R.; Cerf, L.; Junior, W. M.; Zaki, M. J.(2014): Reachability queries in very large graphs: A fast refined online search approach.International Conference on Extending Database Technology, pp. 511-522. Wang, H.; He, H.; Yang, J.; Yu, P.; Yu, J.(2006): Dual labeling: Answering graph reachability queries inconstant time.International Conference on Data Engineering, pp. 75-75. Wei, H.; Yu, J.; Lu, C.; Jin, R.(2014): Reachability querying: An independent permutation labeling approach.Proceedings of the VLDB Endowment, vol. 7, no. 12, pp.1191-1202. Wu, C.; Zapevalova, E.; Chen, Y.; Li, F.(2018): Time optimization of multiple knowledge transfers in the big data environment.Computers, Materials & Continua, vol.54, no. 3, pp. 269-285. Yano, Y.; Akiba, T.; Iwata, Y.; Yoshida, Y.(2013): Fast and scalable reachability queries on graphs by pruned labeling with landmarks and paths.ACM International Conference on Conference on Information & knowledge Management, pp. 1601-1606. Yildirim, H.; Chaoji, V.; Zaki, M. J.(2010): GRAIL: Scalable reachability index for large graphs.Proceedings of the VLDB Endowment, vol. 3, no. 1, pp. 276-284. Yildirim, H.; Chaoji, V.; Zaki, M. J.(2012): GRAIL: A scalable index for reachability queries in very large graphs.VLDB Journal, vol. 21, no. 4, pp. 509-534. Yu, J. X.; Cheng, J.(2010): Graph reachability queries: A survey.Managing and Mining Graph Data, pp. 181-215. Zhang, Z.; Yu, J.; Qin, L.; Zhu, Q.; Zhou, X.(2012): I/O cost minimization:Reachability queries processing over massive graphs.International Conference on Extending Database Technology, pp. 468-479. Zhou, J.; Zhou, S.; Yu, J.; Wei, H.; Chen, Z. et al.(2017):DAGreduction: Fast answering reachability queries.ACM Sigmod International Conference on Management of Data, pp. 375-390. Zhu, A.; Lin, W.; Wang, S.; Xiao, X.(2014): Reachability queries on large dynamic graphs: A total order approach.ACM Sigmod International Conference on Management of Data, pp. 1323-1334. Computers Materials&Continua2018年5期3.2 Query algorithm


3.3 Optimization

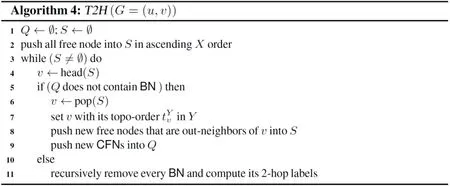
4 Index construction
5 Experiment

5.1 Query time

5.2 Index construction time and index size
6 Conclusions
