Binary Image Steganalysis Based on Distortion Level Co-Occurrence Matrix

Junjia Chen, Wei Lu, , Yuileong Yeung, Yingjie Xue, Xianjin Liu, Cong Lin, and Yue Zhang

1 Introduction

Steganography is the art of hiding secret messages into a host media, analogous to data hiding and invisible watermarking [Feng, Lu, Sun et al. (2016); Feng, Lu and Sun (2015)].To avoid the abuse of steganography, steganalysis [Fridrich and Kodovsky (2012); Yuan,Lu, Feng et al. (2017); Feng, Lu and Sun (2015)] is designed to analyze the embedding trace and detect the existence of secret messages. Since binary image has only 1 bit per pixel and its storage requirement is small, it is widely used in digitizing, processing,transmitting and archiving for a great amount of daily application including document images, handwritings and so on. The demand of distinguishing between original images(cover images) and stego images is raising with the rapidly development of binary steganography [Wu and Liu (2004); Yang and Kot (2007); Yang, Kot and Rahardja (2008);Cao and Kot (2013); Guo and Zhang (2010); Feng, Lu and Sun (2015)]. For this purpose,it is crucial to design a binary steganalytic scheme with high detectability.

Binary images require only 1 bit per pixel and the basic embedding operation in binary images is flipping pixels from black to white and vice versa. Arbitrarily flipping pixels in binary images will create significant distortions, which can be easily detected by human eyes. For this reason, the binary steganographic schemes usually focus on selecting the optimal pixels that introduce less embedding distortions. SHUFFLE [Wu and Liu (2004)]observes the smoothness and connectivity in blocks and find the flippable pixels that preserve the connectivity well. ConnPre [Yang and Kot (2007)] focuses more on the connectivity of blocks and flips the pixels in those connectivity-preserving blocks generated by various block divisions. DPDC [Yang, Kot and Rahardja (2008)] tracks the flippable pixels on the shifted edges using the interlaced morphological wavelet transform.EAG [Cao and Kot (2013)] searches the changeable contour segments along the boundary to find the flippable pixels. Guo et al. [Guo and Zhang (2010)] propose a matrix embedding scheme (denoted as GIM) based on the complete set theory and selects the flippable pixels in the block units. Feng et al. [Feng, Lu and Sun (2015)] designed the scheme focusing on local texture patterns (LTP) and propose a flipping distortion measurement (FDM) to evaluate the distortions introduced by flipping pixels. Syndrome trellis code (STC) [Filler,Judas and Fridrich (2011)] is used to embed the secret messages by flipping the pixels with low distortion values. It can be concluded that flipping pixels with low distortions is an important topic for binary steganography to improving its imperceptibility.

As a countermeasure of steganography, steganalysis focus on finding out the embedding trace and distinguishing the cover and stego images. The previous steganalytic schemes usually constructs a pixel structure model and analyses the difference between the cover and stego images. Chiew et al. [Chiew and Pieprzyk (2010)] utilize pattern histograms(denoted as PHD) of boundary pixels to model images. They calculate the difference between the tested image and the re-embed image, which is used to construct feature vectors for cover and stego images. In the last step of classification, machine learning[Gurusamy and Subramaniam (2017)] and neural network [Yuan, Li, Wu et al. (2017);Yıldızel and Öztü rk (2016)] are always adopted to conduct it. For example, Support Vector Machine (SVM) [Chang and Lin (2011)] is prevalent and effective to classify the feature vectors. Both RLGL and RLCM extract features from the high-order difference of images.RLGL [Chiew and Pieprzyk (2010)] utilizes run length and gap length matrices to model images, and the statistics including mean, variance, kurtosis, and skewness are calculated to form the feature vectors. RLCM [Chiew and Pieprzyk (2010)] utilizes run length and co-occurrence matrices to model images and added some new statistics such as contrast and energy to construct the feature vectors. PMMTM [Feng, Lu and Sun (2015)] constructs different types of pixel meshes and uses pixel mesh Markov transition matrix as features.LP [Feng, Weng, Lu et al. (2017)] traces the “L-shape” patterns to model images and the distributions of the selected patterns are used as steganalytic features. The previous steganalytic schemes use different models but their tasks are same to find out the embedding trace and extract features from it. A more accurate model catching the difference between the cover and stego images can result in a better steganalytic performance.

In this paper, we introduce an image model based on quantified distortion values, namely distortion levels. The distortion measurement we used is FDM, which is the state-of-theart technique to estimate the pixel flippability. For example, it is usually suggested that the best flippable pixels are located at the center of “L-shape” patterns, which is shown in Fig.1, and FDM usually assigns zero value to “L-shape” patterns. Briefly, the pixels with low FDM distortion values are more likely flipped in the steganographic schemes. FDM has an important property that the distortion value of one pixel do not change after flipping if there not exists other flipped pixels in the adjacent area. In this situation, the distortion values of neighbor pixels in 5×5 block would change. For this property, we can find out the embedding trace by analyzing the pixels with low distortion values. In the proposed scheme,we construct the co-occurrence matrix from the low distortion value pixels and their neighbor pixels and re-construct it as steganalytic features. The experimental results show that the proposed scheme achieve good detectability on the state-of-the-art steganographic schemes.

The reminder of this paper is organized as follows. In Section 2, we first analyze the previous steganographic schemes and then introduce the distortion level co-occurrence matrix. The comparison experiments are given in Section 3. Finally, Section 4 concludes the whole papers.

2 The proposed scheme

As is well known, steganalysis and steganography are the opposite research fields. It is important for a good steganalytic method to evaluate the security of steganographic schemes. Therefore, for better constructing our steganalyzer, we analyze some state-of-theart binary image steganography in Section 2.1. Then, in Section 2.2 we introduce the proposed scheme in detail.

2.1 Binary image steganography

There exist many approaches in binary image steganography [Wu and Liu (2004); Yang and Kot (2007); Yang, Kot and Rahardja (2008); Cao and Kot (2013); Guo and Zhang(2010); Feng, Lu and Sun (2015)]. ConnPre is designed to preserve the connectivity the same before and after flipping the embeddable pixels, so that it allows to precisely locate the flipping pixels after the data embedding. It also sets the flippability criteria of the pixels,divides image into interlaced blocks or non-interlaced blocks, and encrypts the cover images to prevent the hostile attack. These conditions guarantee that the hard watermark can be accurately extracted in the stego image according to the precisely locations while maintaining visual quality of the image.

However, ConnPre would not achieve high embedding capacity, because its manipulation in data embedding cannot influence the grid re-establishment in data extraction. Hence, it has to ignore some flippable pixels. Cao et al. [Cao and Kot (2013)] proposed to establish the edge-adaptive grid (EAG) to increase data embedding capacity. Its algorithm, built on three main functional components, contour tracer, content adaptive process and protector,aims at tracing the object boundary and locating flippable pixels. These flippable pixels are always center on the “L-shape” patterns. In Fig. 1, “L-shape” patterns can be easily found on the object boundary, and flipping the center pixel of “L-shape” patterns can remain the boundary smoothness. Therefore, EAG traces the object boundary to locate flippable pixels.With the same purpose of achieving high data embedding capacity, DPDC adopts overlapped wavelet transform to track the shifted edges. Its double processing method allows to embed data in the same 2×2 block, which provides a high capacity approach. The other way to increase the capacity of data embedding, matrix embedding is suggested in GIM, which is designed to reduce the embedding impact.

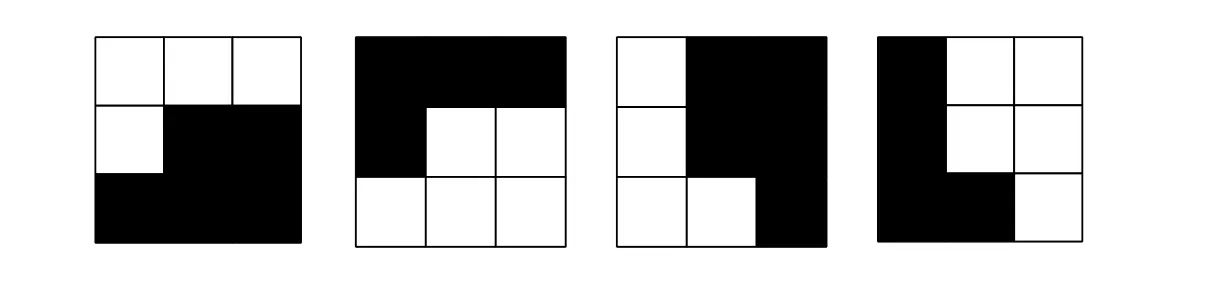
Figure 1: Examples of the “L-shape” pattern

In recent years, it is prevalent to use STC for minimizing additive distortion in steganography [Pevny, Filler and Bas (2010); Feng, Lu and Sun (2015)]. Feng et al. [Feng,Lu and Sun (2015)] initially designed a novel FDM to evaluate the pixel flippability. In their scheme, useless cover image blocks is discarded. Super pixels constructed from those remaining blocks. Combining with corresponding distortion blocks, super pixels are send to be encoded by STC which minimizes additive distortion to embed the data. Their steganographic scheme outperforms other state-of-the-art methods.

Every pixels in image can be evaluated by distortion values which estimate the pixels flippability. The lower the distortion value is, the more possible it is to be embedded. In FDM, calculation of pixel distortion values are based on the neighbor patterns. For example,most of the center pixels of “L-shape” patterns are evaluated as zero value pixels. That implies that these pixels are suitable for embedding. Although flipping the center pixel of“L-shape” patterns in the cover image can maintain visual quality, it would also change the surrounding pixel distortion values in the stego image. Therefore, the difference of distortion maps between cover and stego images are significant. Apparently, our steganalytic features can be constructed from distortion maps of cover and stego images.

2.2 Distortion level co-occurrence matrix

Figure 2: All the patterns in the one class

FDM is designed to calculate the pixel distortion values based on the neighbor patterns and it can generate distortion maps for every binary images. In the 3×3 blocks, there exists 29=512 kinds of patterns in all. FDM firstly classify these 512 patterns based on complement, rotation and mirroring-invariant local texture pattern (crmiLTP). In Fig. 2,we introduce all the patterns in the one class. These patterns can be treated as the same class according to crmiLTP. Hence, after the step of crmiLTP classification, 512 patterns would be classified into 51 classes. The flipping distortion of pixels located (i,j) in cover images X can be calculated as

where Yi,jdenotes the stego image obtained by only changing the pixel located at (i,j),Wtset with the maximal value of Fisher’s criterion after detects all the employed simulators, denotes the weight corresponding to the crmiLTP,anddenote the histogram coefficients corresponding to crmiLTPs with value equal to t which are calculated from images X and Yi,j, respectively.

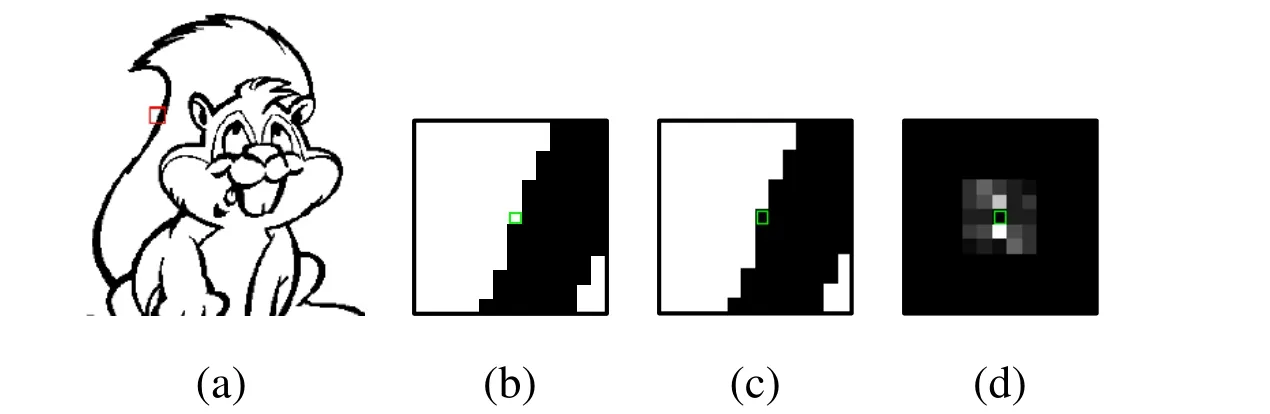
Figure 3: (a) An example of binary cartoon image. (b) Image segment in the red box of (a)and the flippable pixel is in the green box. (c) Image segment after flipping the pixel in the green box. (d) The difference between the distortion maps of (b) and (c)

Actually, flipping a pixel located (i,j) in a cover image would change the classes of neighbor patterns. The flipping pixel distortion values are apparently determined by the change of the classes of neighbor patterns. Therefore, in the stego image, the neighbor pixel distortion values are different with the corresponding position of the cover image. In Fig.3, we introduce image segment of a binary cartoon image and it analyze why we construct our steganalytic features from distortion maps. In Fig. 3(d), we find out that the pixels distortion value in 5×5 block change apparently, except the flipping pixel. The flipping pixel distortion value would preserve the same between cover and stego images if there not exists other flipped pixels in the adjacent area. It provides us a method to construct our cooccurrence matrix and to process dimension selection.

Many steganalytic methods [Chiew and Pieprzyk (2010); Feng, Lu and Sun (2015); Feng,Weng, Lu et al. (2017); Fridrich and Kodovsky (2012); Denemark, Sedighi, Holub et al.(2014)] always construct high dimensional co-occurrences matrices to represent the features of images. Then they also utilize classifier, such as SVM and Ensemble Classifier(EC) [Kodovsky, Fridrich and Holub (2012)] to classify the features extracted from cover and stego images. In this paper, we construct two-order co-occurrence matrices on the distortion level maps for cover and stego images. After features construction, for fair comparison, we also use SVM to classify features extracted from distortion maps of cover and stego images.

Before we construct the two dimensional matrix, we quantize distortion maps into several levels. With constraint of the size of samples, five thousand of binary cover images, we uniformly quantize distortion map into 32 levels based on the maximum value and the minimum value of distortion map. The step of the quantitative process is:

where Dminand Dmaxdenote the minimum value and the maximum value of distortion map, respectively.

The next step, co-occurrence matrix from two neighboring values of the quantized distortion level map are:

where [∎] is the Iverson bracket, which is equal to 1 if logical proposition inside the bracket is true, and 0 otherwise,mandndenote the size of images, di,jdenotes distortion levels located (i,j) in maps. However, flipping one pixel would change neighbor pixel distortion values in stego images. If we only use the distortion level of one pixel and its right adjacent pixel distortion level to construct the co-occurrence matrix, it would lose much key features on distortion level maps. Therefore, we re-construct the co-occurrence matrix:

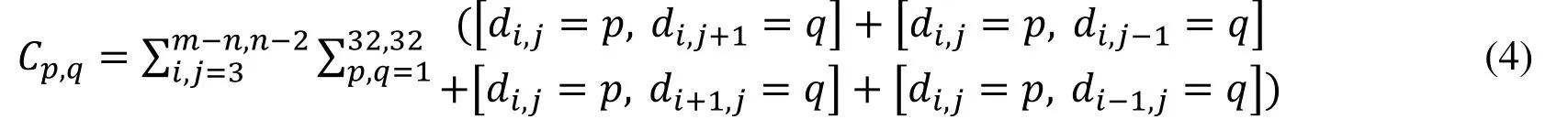
We have also adopted eight directions neighboring pixel distortion values to re-construct the co-occurrence matrix. However, in our empirical study, the construction of cooccurrence matrices for vertical and horizontal directions achieve better performance.

In the step of distortion level co-occurrence matrix (DLCM) dimensions selection, we first select the dimension of the first order. In this order, we select the half dimensions, from 32 to 16. We simply remove the second half of this order (i.e. we ignore those di,j∈[17,32]),because many steganographic schemes always flip the pixels with low distortion values.Then, we calculate the occurrence numbers of the neighbor pixel distortion values in cover and stego distortion maps. In the second order, we remain the top 18 levels of the occurrence number of distortion values. Therefore, the proposed feature dimensions are reduced to 16×18=288.

3 Experimental result

3.1 Experiment setup

In this section, we evaluate the proposed 288D DLCM on several steganographic schemes which introduced in Section 2.1. ConnPre, EAG, DPDC, GIM and LTP would be selected as steganographic test schemes. ConPre and EAG search flippable pixels, whose location cannot influence extraction step, along object boundary to embed data. DPDC adopts overlapped wavelet transform to track the shifted edges to embed data. GIM uses the matrix embedding method to achieve high capacity. STC encoder for minimizing additive distortion is adopted in LTP scheme to gain better information security.

Figure 4: Demonstrations of different types of binary images. The types of binary images are (from left to right) “cartoon”, “CAD”, “texture”, “mask”, “handwriting” and “document”

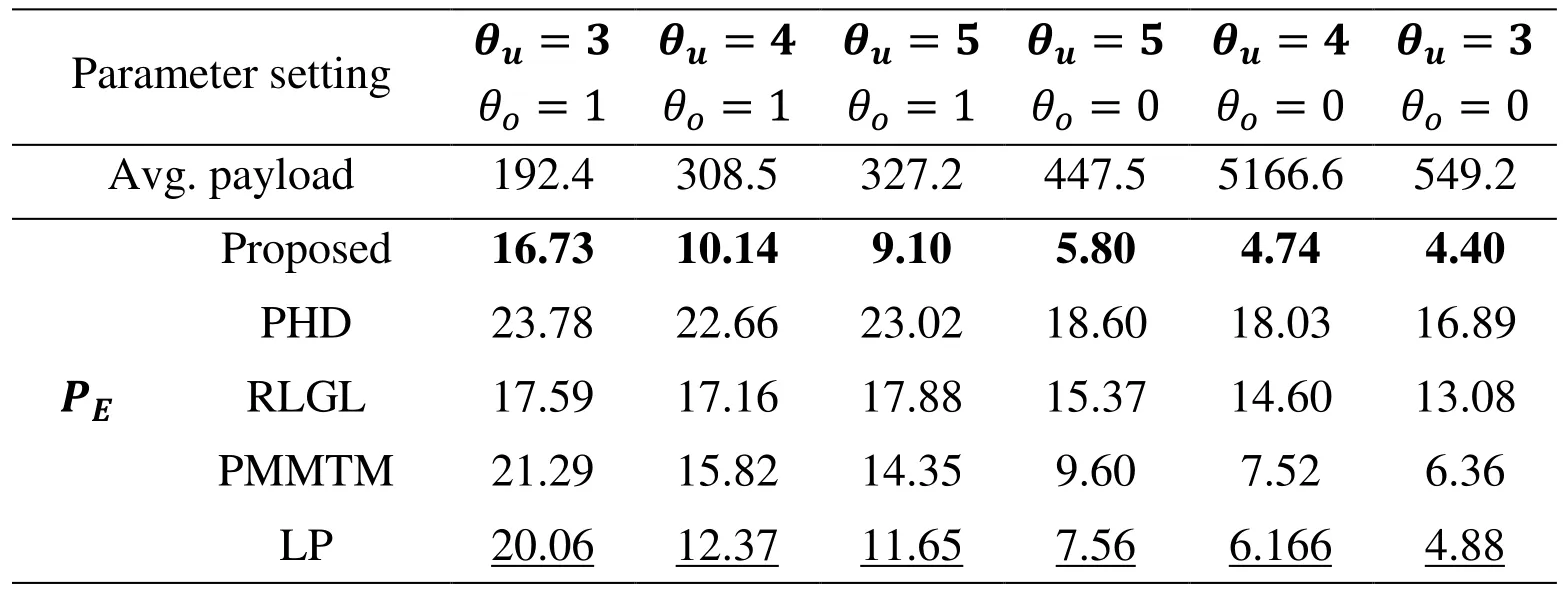
Table 1: Comparison of different features when attacking ConnPre

All the experiments are conducted on the Binary Images comprised of Various Contents(BIVC) database [Feng, Lu and Sun (2015)]. BIVC database contains 5000 images with size of 256×256. The database is consist of many kinds of images, such as cartoon, CAD graph, texture, mask, handwriting and document (see Fig. 4). All the experimental results are reported in Section 3.2 and all steganographic features are classified by SVM. It classify all the features based on the gaussian kernel and use grid optimization to search the best parameters. Every experiments adopt 5 folder cross-validation on searching best parameters. Then, half of the images randomly selected from database are used for training while the rest for testing. All the experimental performance can be evaluated using the error rate PE, defined as

where PFAand PMDdenote the probabilities of false alarm and missed detection,respectively.

3.2 Comparison with other approaches

In order to better evaluate the proposed 288D DLCM performance, we compare our scheme with several prior arts. Some state-of-the-art steganalytic features [Chiew and Pieprzyk (2010); Feng (2015, 2017)] are employed for comparison. PHD utilizes pattern histograms from boundary pixels to model images. RLGL uses run length and gap length matrices to model images and extract features from the high-order difference of images.PMMTM and LP can achieve better performance than two former schemes. PMMTM uses different types of pixel meshes and constructs Markov transition matrix as features. LP focuses on “L-shape” patterns, because “L-shape” patterns are always suitable to flip. For fair comparison, all these steganalytic features are classified by SVM through grid optimization to search best parameters.

Table 2: Comparison of different features when attacking EAG

Table 3: Comparison of different features when attacking DPDC

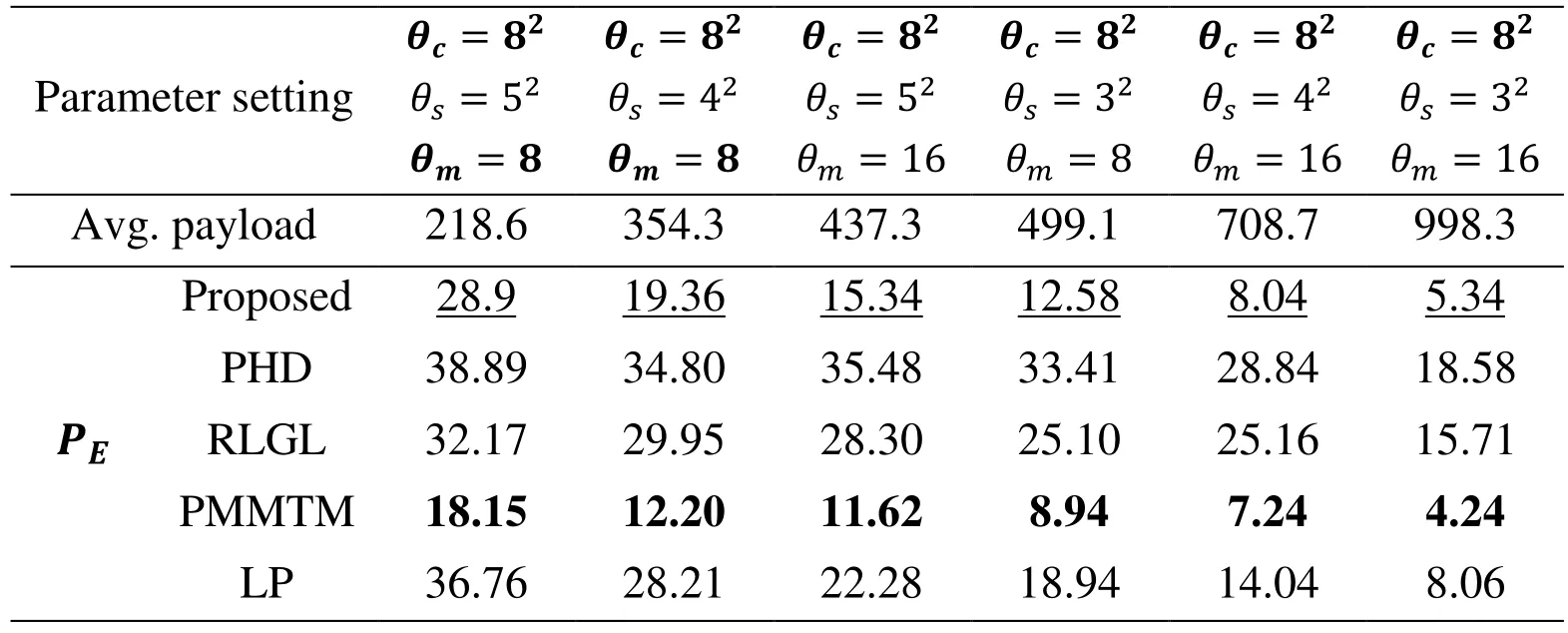
Table 4: Comparison of different features when attacking LTP

Parameters θuand θoin Tab. 1 are the block size and overlap mode (0 for non-overlapped and 1 for over lapped), respectively. These parameters can be used to adjust ConnPre payload adaptively. In Tab. 4, θc, θs, θmare the numbers of elements in the cover vector,superpixel, and message segment in LTP, respectively. θrin Tab. 5 denotes the cardinality of the complete set. In all tables, the best experimental results are in bold type and the second-best are with underline.

The proposed 288D DLCM outperform the others on ConnPre, EAG, DPDC steganographic method, shown in Tabs. 1-3. Compared with other steganalytic features when attacking θu=3, θo=1 ConnPre in Tab. 1, the error rate of the proposed features decrease by 3.33%. Similarly, the error rate decrease by 3.76% on EAG and 1.45% on DPDC. These methods similarly flipped the pixels of some specific patterns which meet the designed flipping criterion. Therefore, the proposed feature extraction scheme can exactly capture flipped traces of these methods.

However, the proposed features do not perform well on LTP and GIM, particularly on LTP.

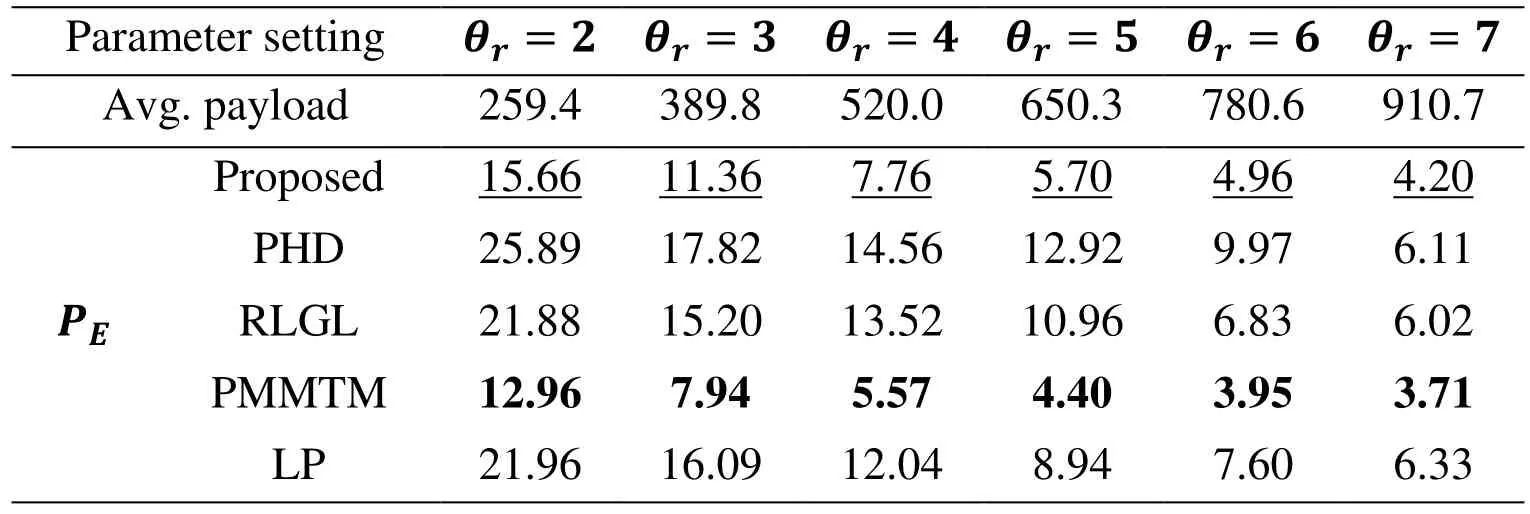
Table 5: Comparison of different features when attacking GIM

The error rate is higher than PMMTM by 10.15% when θc=82, θs=52, θm=8 in Tab.4. It is hard for the proposed features to capture flipped traces of LTP method. Therefore,in the future we would improve our method to model images and aim at accurately detecting LTP and GIM.

4 Conclusion

In this paper, we propose a novel steganalytic scheme based on distortion level cooccurrence matrix. In order to better model image features, flipping distortion measurement(FDM) is adopted in this paper. The FDM is the state-of-the-art technique to estimate the pixel flippability. The property of FDM enable us to capture embedding traces through constructing the co-occurrence matrix of the pixels of low distortion values and their neighbor pixels. The proposed steganalytic scheme outperform the others state-of-the-art steganalytic scheme on ConnPre, EAG and DPDC steganographic methods. However, it is hard for the proposed steganalytic method to accurately detect LTP and GIM. In the future,we would try to improve the performance on these kinds of steganalytic schemes.

Acknowledgement:This work is supported by the National Natural Science Foundation of China (No. U1736118), the Natural Science Foundation of Guangdong (No.2016A030313350), the Special Funds for Science and Technology Development of Guangdong (No. 2016KZ010103), the Key Project of Scientific Research Plan of Guangzhou (No. 201804020068), the Fundamental Research Funds for the Central Universities (No. 16lgjc83 and No. 17lgjc45), the Science and Technology Planning Project of Guangdong Province (Grant No. 2017A040405051). The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Cao, H.; Kot, A.(2013): On establishing edge adaptive grid for bi-level image data hiding.IEEE Transactions on Information Forensics and Security, vol. 8, no. 9, pp. 1508-1518.

Chang, C.; Lin, C.(2011): Libsvm: A library for support vector machines.ACM Transactions on Intelligent Systems and Technology, vol. 2, no. 3, pp. 27.

Chiew, K. L.; Pieprzyk, J.(2010): Binary image steganographic techniques classification based on multi-class steganalysis.Information Security, Practice and Experience, pp. 341-358.

Chiew, K. L.; Pieprzyk, J.(2010): Blind steganalysis: A countermeasure for binary image steganography.International Conference on Availability, Reliability and Security, pp. 653-658.

Chiew, K. L.; Pieprzyk, J.(2010): Estimating hidden message length in binary image embedded by using boundary pixels steganography.International Conference on Availability, Reliability and Security, pp. 683-688.

Denemark, T.; Sedighi, V.; Holub, V.; Cogranne, R.; Fridrich, J.(2014): Selection channel-aware rich model for steganalysis of digital images. InInformation Forensics and Security (WIFS), IEEE International Workshop, pp. 48-53.

Feng, B.; Lu, W.; Sun, W.(2015): Binary image steganalysis based on pixel mesh markov transition matrix.Journal of Visual Communication and Image Representation, vol. 26, pp.284-295.

Feng, B.; Lu, W.; Sun, W.(2015): Novel steganographic method based on generalize kdistance n-dimensional pixel matching.Multimedia Tools and Applications, vol. 74, no. 21,pp. 9623-9646.

Feng, B.; Lu, W.; Sun, W.(2015): Secure binary image steganography based on minimizing the distortion on the texture.IEEE Transactions on Information Forensics and Security, vol. 10, no. 2, pp. 243-255.

Feng, B.; Lu, W.; Sun, W.; Huang, J.; Shi, Y.(2016): Robust image watermarking based on tucker decomposition and adaptive-lattice quantization index modulation.Signal Processing: Image Communication, vol. 41, pp. 1-14.

Feng, B.; Weng, J.; Lu, W.; Pei, B.(2017): Steganalysis of content-adaptive binary image data hiding.Journal of Visual Communication and Image Representation, vol. 46, pp. 119-127.

Filler, T.; Judas, J.; Fridrich, J. J.(2011): Minimizing additive distortion in steganography using syndrome-trellis codes.IEEE Transactions on Information Forensics and Security, vol. 6, no. 3, pp. 920-935.

Fridrich, J. J.; Kodovsky, J.(2012): Rich models for steganalysis of digital images.IEEE Transactions on Information Forensics and Security, vol. 7, no. 3, pp. 868-882.

Guo, M.; Zhang, H.(2010): High capacity data hiding for binary image authentication.International Conference on Pattern Recognition, pp. 1441-1444.

Gurusamy, R.; Subramaniam, V.(2017): A machine learning approach for MRI brain tumor classification.Computers, Materials & Continua, vol. 53, no. 2, pp. 91-108.

Kodovsky, J.; Fridrich, J. J.; Holub, V.(2012): Ensemble classifiers for steganalysis of digital media.IEEE Transactions on Information Forensics and Security, vol. 7, no. 2, pp.432-444.

Pevny, T.; Filler, T.; Bas, P.(2010): Using high-dimensional image models to perform highly undetectable steganography.International Workshop on Information Hiding, pp.161-177.

Wu, M.; Liu, B.(2004): Data hiding in binary image for authentication and annotation.IEEE Transactions on Multimedia, vol. 6, no. 4, pp. 528-538.

Yang, H.; Kot, A. C.(2007): Pattern-based data hiding for binary image authentication by connectivity-preserving.IEEE Transactions on Multimedia, vol. 9, no. 3, pp. 475-486.

Yang, H.; Kot, A. C.; Rahardja, S.(2008): Orthogonal data embedding for binary images in morphological transform domain-a high-capacity approach.IEEE Transactions on Multimedia, vol. 10, no. 3, pp. 339-351.

Yıldızel, S.; Öztürk, A.(2016): A study on the estimation of prefabricated glass fiber rein forced concrete panel strength values with an artificial neural network model.Computers,Materials & Continua, vol. 52, no. 1, pp. 42-51.

Yuan, C.; Li, X.; Wu, Q. J.; Li, J.; Sun, X.(2017): Fingerprint liveness detection from different fingerprint materials using convolutional neural network and principal component analysis.Computers, Materials & Continua, vol. 53, no. 3, pp. 357-371.

Yuan, Y.; Lu, W.; Feng, B.; Weng, J.(2017): Steganalysis with cnn using multi-channels filtered residuals.International Conference on Cloud Computing and Security, pp. 110-120.