Watermark Embedding for Direct Binary Searched Halftone Images by Adopting Visual Cryptography

Yangyang Wang, Rongrong Ni, , Yao Zhao and Min Xian

1 Introduction

With the development of computer science and internet technology, more and more multimedia contents such as images are shared on the internet. But there are still many materials need to be printed in our daily life. However, many materials are being copied or modified illegally. Therefore, the protection of printed materials becomes more and more significant.

Printed images are also called halftone images [Bayer (1973)]. Due to the limitation of printers, the printed images can only use two tones (ink for black and no ink for white) to simulate the multitone grayscale images. To transform grayscale images into halftone images, many different halftone methods have been developed, including Direct Binary Search (DBS) [Analoui and Allebach (1992)], Ordered Dithering (OD) [Ulichney (1993)],and Error Diffusion (ED) [Floyd and Steinberg (1976)]. Among these methods, the halftone images generated by DBS gain much higher visual quality than others.

Since the halftone images only use two tones, the traditional digital watermark methods cannot be applied to halftone images directly, such as methods that are introduced in Keissarian et al. [Keissarian (2009); Cao, Zhou, Sun et al. (2018)]. Therefore, two kinds of methods to embed watermark into halftone images have been developed in recent years.

The methods in the first category are proposed to embed a secret binary stream into the cover halftone images. Then these methods retrieve the watermark from the stego halftone image by applying the corresponding extraction algorithms. In Fu et al. [Fu and

Au (2000); Pei and Guo (2006); Guo (2007); Bulan, Sharma and Monga (2010); Guo and Liu (2011)], they proposed methods to embed watermark by modifying the pixel values in spatial domain. A method by changing the coefficient values in the wavelet transform domain to embed watermark was proposed in Luo et al. [Luo, Zhao, Huang et al. (2007)].In Amini et al. [Amini, Yaghmaie and Sadreazami (2010)], the watermark was embedded by merging the singular values of the selected frequency band of the cover image and the watermark. By changing the point spread function, a secret binary stream was able to embed into the DBS halftone images in Guo et al. [Guo, Su, Liu et al. (2012)].

The methods in the second category are proposed to embed watermark into multiple halftone images. In general, two halftone images are used to carry watermark in these methods. When the two halftone images are overlaid, the watermark is appearing. The first method of this category was proposed in Fu et al. [Fu and Au (2001)]. After that, a method named DHCED was proposed in Fu et al. [Fu and Au (2003)] which improved the performance. Pei et al. [Pei and Guo (2003)] used Noise-Balanced Error Diffusion to embed watermark, and gained the similar performance with [Fu and Au (2003)]. Guo et al. [Guo, Au, Fang et al. (2011)] embedded the watermark into both of the two cover halftone images. In Sanchev et al. [Sanchev, Nayak and Pradhan (2014)], the watermark was embedded into Multiscale Error Diffusion halftone images. Guo et al. [Guo and Liu(2011)] embed watermark into halftone images, which were generated by the least-meansquare (LMS) method. The methods in the second category can be applied in some special halftone methods such as error diffusion. But these methods cannot be applied into the halftone images generated by the efficient Direct Binary Search halftone.

In this paper, due to the perfect performance of efficent DBS, we propose two methods to embed watermark into efficent DBS halftone images. The first method which is called Adjusted Direct Binary Search (ADBS) can only embed watermark into one halftone image. Considering the improvement of the visual quality, the second method called Dual Adjusted Direct Binary Search is proposed, which is capable to embed watermark into both of the two cover halftone images.

The rest of the paper is organized as follows. Section 2 reviews the Efficient Direct Binary. Search. Section 3 introduces the first method, Adjusted Direct Binary Search.Section 4 introduces the second method, Dual Adjusted Direct Binary Search. The experimental results are given in Section 5. And Section 6 draws the conclusion.

2 Review of efficient direct binary search

The DBS is used to make the halftone image looks more similar with the grayscale imageby minimizing difference between them on human visual system. The method has twosteps. The first step is calculating the difference of grayscale image and halftone image inhuman visual system. The second step is trying to toggle or swap pixels in halftone imageto reduce the total difference of them on human visual system. But calculating the totalerror costs a lot. So, Analoui et al. [Analoui and Allebach (1992)]proposed a method, called efficient Direct Binary Search, to solve this problem. The efficient DBS is then deduced as bellow.

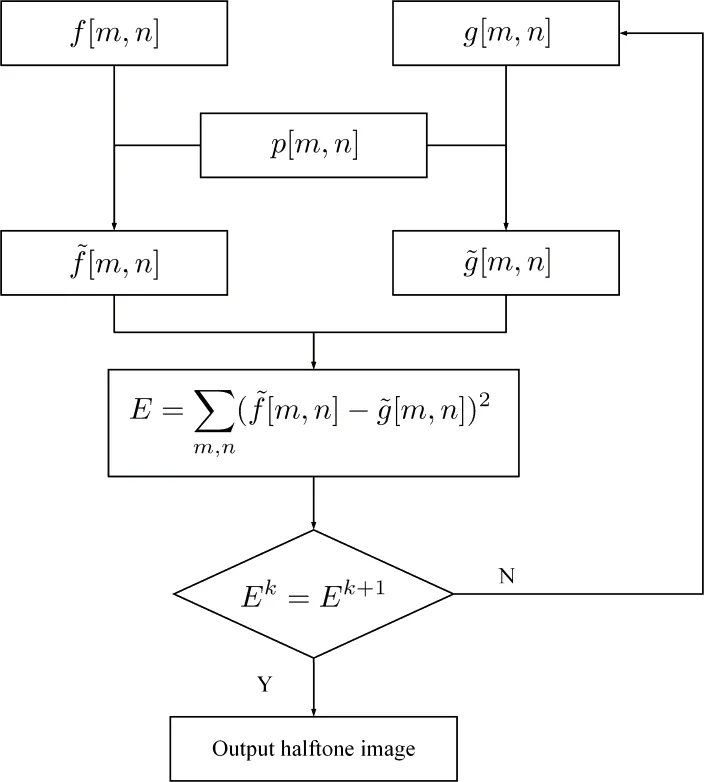
Figure 1: Flowchart of Direct Binary Search

Assumimgf(u,v)andg(u,v)are the grayscale and halftone image, respectively.p(u,v)denotes the Point Spread Function. Then, the corresponding images on human visual system are represented as(x,y)and(x,y), which can be calculated by the following formulas.

So the difference between the grayscale and halftone images on the human visual system can by calculated as

Then the total square error is used as the measure of the differences between the grayscale image and the halftone image can be calculated as

As for the discretized images, the total square error can be transformed as

where [m,n]is a sample of (x,y)andis the convolution of the Point Spread Function, which can be obtained by

and

is the difference between the grayscale image and halftone image.

The iterative method of efficient DBS is applied to minimize the total square error of the grayscale image and halftone image on the Human Visual System. In every iteration of the efficient DBS, it tries to toggle a pixel or swap a pair of pixels and calculates the incremental error. Then the manipulation that corresponding to the minimum incremental error is chosen. The incremental error of toggle manipulation atis

where

and

Andis used to save intermediate results and reduce the amount of calculation. The incremental error of swap manipulation betweenandis

wherea0,a1are calculated as Eq. (9). According to the Eq. (10),cpeis influenced by thee[m,n], which is associated withg[m,n]. So during the iteration process,cpeshould be updated. For pixel [m0,n0], if the toggle manipulation is selected

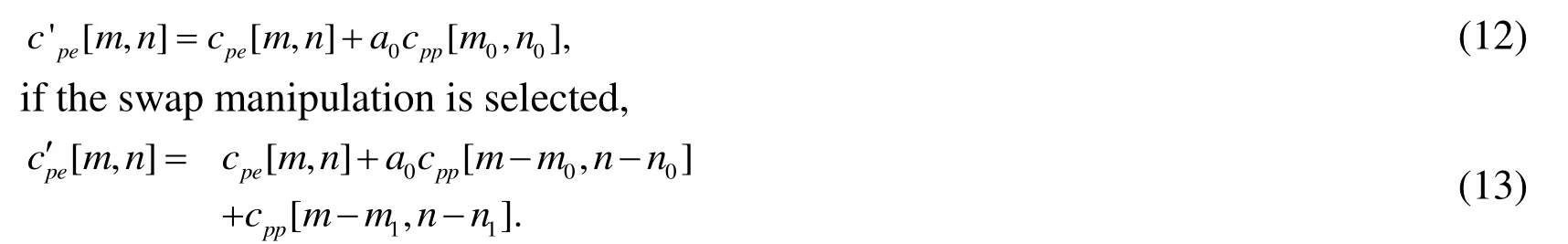
In summary, the procedure of the efficient Direct Binary Search will follow the steps below.

3 Data hiding by adjusted direct binary search

In visual cryptography, the goal of the data hiding method in halftone images is that the watermark can be displayed when the two halftone images are overlaied. Fig. 2 gives some example to help understand this. In Fig. 2, (a) and (b) represent the two halftone images, and (c) represents the overlaid result. In the first row, (a) and (b) are in the same tone, the result looks relatively white. And in the second row, (a) and (b) are in the opposite tones, the result looks relatively dark. To achieve this goal, if the pixel of the watermark image is white, the two halftone images are better to be in the same tone, if it is black, the two halftone images are better to be in the opposite tones.

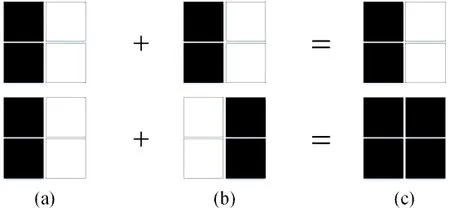
Figure 2: Example of two halftone images are overlaid

Letanddenote the first and second grayscale images. Letanddenote the watermark image. The values of,, andare 1(for black) or 0 (for white). Therefore,

could be used to represent if the watermark has been successfully embedded at position, wheremean XOR. In watermark image, for white pixels, theis 0 andshould be contrast to. So that ifis 0,should be 1, it means the watermark has been successfully embedded at pixel. On the other hand, ifis 1,is 0, that means the watermark has not been embedded at pixel. Therefor, the total number of the pixels which have been successfully embedded is

In our first data hiding method, called Adjusted Direct Binary Search (ADBS), we fix the first halftone image and adjust the second halftone image to successfully embed watermark as well as achieve the high visual quality. So in ADBS, the optimization goal can be wrote as

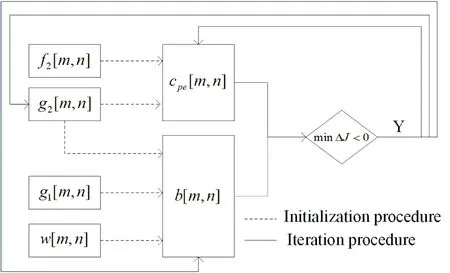
Figure 3: Procedure of ADBS

thus, for toggle manipulation at position00[m,n]In summary, the procedure of the Adjusted Direct Binary Search in the Fig. 3 follows the steps below.

4 Data hiding by dual adjusted direct binary search

Since the ADBS fixed the first halftone image and only embed watermark into the second halftone image, the second halftone image’s visual quality will be more poorer than the first one. So, we propose a method, called Dual Adptive Direct Binary Search (DADBS),to embed watermark into both of the two halftone images.

In DADBS, since both of the two halftone images need to be modified to embed the watermark, the visual quality of both of the two halftone images should be considered.Therefore, in DADBS, the optimization goal can be rewrote as

Figure 4: Procedure of ADBS

5 Experimental results

In this section, the result for ADBS and DADBS are presented. Because the DBS methods will produce the most good visual quality in all halftone methods, so in this paper we compared the visual quality of the halftone image generated by the proposed methods with the Error Diffusion method not the Error Diffusion based visual watermark method. In the experiments, the size of all images areWe use the visual error between the halftone and grayscale image to measure the visual quality of the halftone iamge. It can be calculate by Eq. (6), and the visual quality will be more worse with higher error. The watermark embedding rate is calculate as

the embedding rate is more higher, the watermark is more clear when the two halftone images are overlaid.

Fig. 5 shows an example of ADBS. That we use the native DBS method to generate the first halftone image, and the ADBS method (hereα=0.24, search widthn=3) to generate the second halftone image. When the two halftone images are overlaid a logo of visual studio is appeared.

Fig. 6 shows the results of visual error and the embedding rate results of the two methods.To compare the results of ADBS and DADBS, we only plot the second image’s visual error of both the two methods. It’s easy to find out the visual error is becoming more and more higher as the embedding rate increased. As for in the same embedding rate, the DADBS will get a more slower visual error.

Tab. 1 shows the visual error of some typical Error Diffusion and Ordered Dithering halftone images. It’s easy to find out the halftone image with the smallest visual error is generated by the Floyd Kernel based Error Diffusion method. But it is visual error is still bigger than the visual error of the halftone image that generated by ADBS of DADBS(less than 76).

Figure 5: From topleft to buttomright is the orginal image, the first halftone image generated by DBS, the second halftone image generated by ADBS, the overlay of the two halftone image

Table 1: The visual error of different error diffusion methods

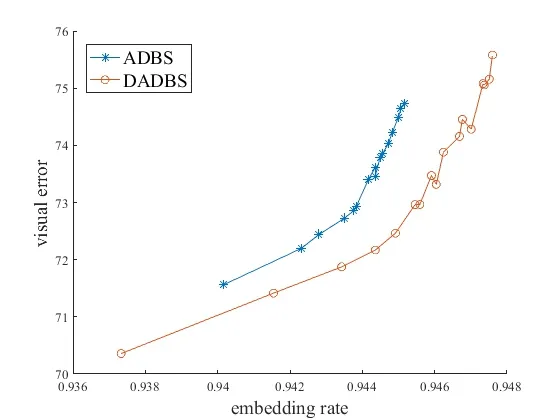
Figure 6: The visual error embedding rate results of ADBS and DADBS. The original images are both lena

6 Conclusion

This work presents two halftone watermarking methods, ADBS and DADBS. ADBS and DADBS can both embed a visual watermark into two efficient DBS generated halftone images. When the two halftone images are overlaid, the watermark will be appeared.According the experimental results, the proposed methods not only provide the methods to embed watermark, but also generate a good visual quality than the Error Diffusion based watermark methods, and the halftone images’ visual quality even better than the halftone image which generated by Error Diffusion.

Amini, M.; Yaghmaie, K.; Sadreazami, H.(2010): Error diffusion halftone image watermarking based on svd-dwt technique.Machine Vision & Image Processing, pp. 1-4.

Analoui, M.; Allebach, J. P.(1992): Model-based halftoning using direct binary search.Proceedings of SPIE-The International Society for Optical Engineering, vol. 1666, pp.1666-1666-13.

Bayer, B. E.(1973): An optimum method for two-level rendition of continuous-tone pictures.International Conference on Comunications, pp. 11-15.

Bulan, O.; Sharma, G.; Monga, V.(2010): Orientation modulation for data hiding in clustered-dot halftone prints.IEEE Transactions on Image Processing, vol. 19, pp. 2070-2084.

Cao, Y.; Zhou, Z.; Sun, X.; Gao, C.(2018): Coverless information hiding based on the molecular structure images of material.Computer, Materials & Continua, vol. 54, no. 2,pp. 197-207.

Floyd, R. W.; Steinberg, L.(1976): An adaptive algorithm for spatial gray scale.Sid International Symposium Digest of Technical Papers, vol. 17, pp. 75-77.

Fu, M.; Au, O.(2001): Data hiding in halftone images by stochastic error diffusion.Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing, pp. 1965-1968.

Fu, M.; Au, O.(2003): Steganography in halftone images: Conjugate error diffusion.Signal Process, vol. 83, pp. 2171-2178.

Fu, M.; Au, O.(2000): Data hiding by smart pair toggling for halftone images.IEEE International Conference on Acoustics, vol. 6, pp. 2318-2321.

Guo, J.(2007): A new model-based digital halftoning and data hiding designed with lms optimization.IEEE Transactions on Multimedia, vol. 9, pp. 687-700.

Guo, J.; Liu, Y.(2011): Halftone images ecurity improving using over all minimal-error searching.IEEE Transactions on Image Processing, vol. 20, pp. 2800-2812.

Guo, J.; Su, C.; Liu, Y.; Lee, H.; Lee, J.(2012): Oriented modulation for watermarking in direct binary search halftone images.IEEE transactions on image processing, vol. 21,pp. 4117-4127.

Guo, Y.; Au, O.; Fang, L.; Tang, K.(2011): Data hiding in halftone images by dual conjugate error diffusion.Proceedings of Asia-Pacific Signal and Information Processing Association Annual Summit and Conference.

Keissarian, F.(2009): A new quadtree-based image compression technique using pattern matching algorithm.Computer, Materials & Continua, vol. 12, no. 4, pp. 137-143.

Luo, H.; Zhao, Z.; Huang, J.; Lu, Z.(2007): Halftone image watermarking based on the binary pseudo-wavelet transform.International Conference on International Information Hiding & Multimedia Signal Processing, vol. 1 pp. 299-302.

Pei, S.; Guo, J.(2003): Data hiding in halftone images with noise-balanced error diffusion.IEEE Signal Processing Letters, vol. 10, pp. 349-351.

Pei, S.; Guo, J.(2006): High-capacity data hiding in halftone images using minimalerror bit searching and least-mean square filter.IEEE Transactions on Image Processing,vol. 15, pp. 1665-1679.

Sanchev, S.; Nayak, A.; Pradhan, T.(2014): Data hiding in halftone images using mathematical morphology and conjugate ordered dithering.International Conference on High Performance Computing & Applications, pp. 1-7.

Ulichney, R. A.(1993): The void-and-cluster method for dither array generation.Proceedings of SPIE - The International Society for Optical Engineering, vol. 1913, pp.1913-1913-12.