江苏省农业主产区农业全要素生产率增长的分解研究
——以苏北苏中32个县(市)为例
张 琛
(中共江苏省委党校经济学教研部,江苏 南京 210009)
一、引言
从2015年年底召开的中央农村工作会议,到习近平总书记在2016年12月的中央政治局常委会上的发言中均强调农业生产的供给侧改革的重要性。2017年中央一号文件更是提出:“把深入推进农业供给侧结构性改革作为新的历史阶段农业农村工作主线”。为了配合深入农业供给侧结构性改革,地方政府需要思考未来进一步提高农业生产效益的具体措施。研究农业全要素生产率,就是研究农业科技的更新速度、农业生产管理水平、农业资源配置效率和农业的规模合理性,探寻潜在的影响因素和挖掘产业潜力。尽管目前学界对全要素生产率的分解研究已经形成了相对完善的技术手段,但是对除河南、四川外的一些农业主要产出区域的研究相对缺乏。
江苏省农业生产条件得天独厚,但是随着工业化进程的加深和国际贸易的不断发展,省内区域间的产业分工结构发生了巨大的变化。根据《江苏省统计年鉴》数据显示,从产出方面看,2015年苏北苏中地区第一产业产值占总产值的75.7%。粮食产量占全省总量的86.5%;油料产量占全省总量的84.5%;棉花产量占全省总量的96.7%。从投入方面看,2015年苏北苏中地区农林牧渔业从业人数占全省该投入的85.2%;农业机械总动力占全省该投入的84%;化肥施用量占全省该投入的89.9%;农作物总播种面积占该投入的84.9%。因此,无论从农业的生产规模还是从农产品产量看,苏北和苏中地区均占主导地位。可以说江苏省农业的主产区集中在苏北和苏中地区,研究江苏省农业生产效率问题,主要是研究苏北苏中地区的农业生产效率问题。因此,本文将研究对象的范围限定在苏北和苏中的县域地区。此外,由于苏南的农村人口大量存在兼业情况,在统计上这些从业人员很难被区分开。这就造成了苏南地区的农业劳动力投入被高估,进而影响计量结果,这也是本文限定研究范围为苏北和苏中地区的另一原因。
全要素生产率(TFP)是产出发生变化时,要素不能解释的部分,是量化一项生产活动效率的一种综合指标。最早由Solow(1957)提出。然而索罗增长模型在强调全要素生产率是增长的源泉的同时,又假定全要素增长率为外生给定,Romer[1]认为“索罗模型是通过假定增长来解释增长的”。
为了进一步地深入研究全要素生产率,Kumbhakar[2]做了开创性的工作,对全要素增长率变化进行了比较彻底地分解,分为技术进步、技术效率变化、配置效率和规模经济性。在此基础上全要素生产率成为一个可以清晰反映要素解释的部分外增长源泉的综合变量。
现行的全要素生产率研究一般从对技术效率的分解开始。分离出生产效率的方法发展为主要的两类:一类是利用计量经济分析手段进行估计的参数分析法,另一类是利用数学规划为主要手段的非参数分析法。Battese[3]开创了随机前沿生产函数估计法(Stochastic Frontier Analysis,SFA),是参数分析法中的主流方法。非参数分析法以数据包络分析(Data Envelopment Analysis,DEA)为主,其与 Malmquist指数相结合的DEA-Malmquist方法在应用研究中最为常见,由Fare[4]开创性地用于生产率研究。
在相关领域的应用研究方面,吴清华[5]从增长核算的角度把农业全要素生产率分解为技术进步、规模经济、灌溉设施的效率和农村公路的贡献率,并研究了农村基础设施对农业全要素生产率的影响。对于模型和方法的选择方面,余康[6]指出,DEA法可能出现难以解释的技术退步现象,而SFA可以避免这种问题。此外,不少学者对传统的DEA和SFA方法进行改进。其中使用DEA-Malmquist方法的学者仍是主流,如尹朝静[7]通过 DEA-Malmquist法对我国1998-2011年间30省的农业全要素生产率进行测算。
综上所述,从研究方法的选取到最后的分解,对于农业全要素增长率的研究学界已经形成了一个较为成熟的研究思路,但是国内相关领域对微观主体的关注度不够,对我国各个区域、省份内部的农业全要素增长率研究也较为缺乏。
因此,本文选用农业全要素生产率作为切入点,明确农业全要素生产率增长和技术进步的关系等理论基础的前提下,以江苏省32个县(市)为研究对象,利用随机前沿分析法(SFA)将各个县(市)在各个时期的技术效率损失估算出来。在此基础上,利用Kumbhakar[2]的分解方法将32个县(市)在“十二五”时期的农业全要素生产率增长分解为技术进步、技术效率变化、规模经济性和配置效率四个部分。通过对农业全要素生产率增长的分解,明确促进或者制约江苏省农业全要素生产率增长的源泉。
二、理论基础和模型选择
(一)理论基础
随机前沿分析方法从生产函数模型出发,其独特之处在于将传统的误差项分为两个部分:技术非效率项和随机误差项。技术非效率项反映了生产单元在利用技术进行生产时因为管理组织或者技术利用不到位等原因而产生的效率损失。
常用的随机前沿模型有两种类型:第一类是由 Battese 和 Coelli[8]提出,简称 BC(1992)模型,第二类仍是 Battese 和 Coelli[9]提出,简称BC(1995)模型。
Battese和 Coelli[8]提出了一个随机前沿模型,其技术非效率项被假设为可以随时间发生系统性变化的,独立同分布的截尾正态分布,并且可以适用于平衡或不平衡面板数据。具体形式如下:
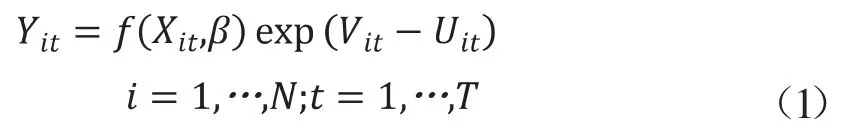
其中,Yit表示t时期第i个生产单元的产出;Xit表示t时期第i个生产单元的投入向量,β为待估参数,Vit表示随机误差项,与技术非效率项Uit相互独立,独立同分布于正态分布 。
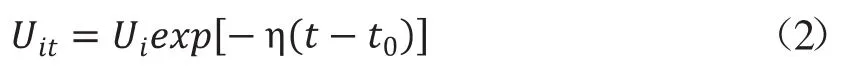
Uit代表不同生产单元在不同时间的效率损失,除了BC(1992)以外,很多文献对Ui的形式有不同的假定。本文假定Ui服从独立同分布的截尾正态分布,其均值是μ,在零点左侧断尾,也就是说Ui为非负项。式(2)中的关系代表同一生产单元的技术非效率项随时间的变化,需要乘以一个时变系数,是表示技术效率变化程度的一个系数,当η>0,技术非效率项随时间推移下降,若η<0,则随时间推移上升,若η=0,技术非效率项不变。在随机前沿分析中考虑这种形式的技术非效率项时间变化,称为时变(Time-varying)随机前沿模型。一般情况下,η>0,称为时变衰减模型。
因此,可以从原生产函数的角度推算出技术效率(technological efficiency,TE)的表达式:η>0,则 TE 递增,η<0,则递减。
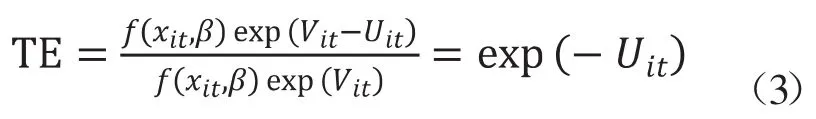
根据 Battese[3]的研究,在计算过程中,为了估计模型,用代替 和 。其中,参数γ在0和1之间取值,表示技术无效率项引致的对生产前沿面的偏离程度。参数γ的值越大,表示技术效率的损失量越大,当γ=1时,实际产出偏离技术前沿面完全由生产的低效率引起,与随机误差项无关。反之,γ越小,表明技术损失的量越小,当γ=0时,表示实际产出的偏离完全由随机误差项引起,不应当使用随机前沿分析法。
BC(1995)模型的具体形式和 BC(1992)模型相同:
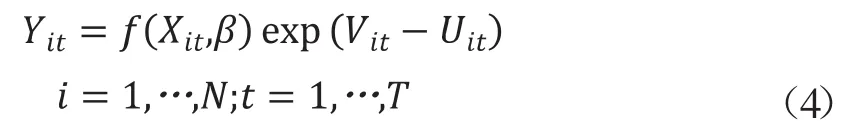
不同之处在于,Uit被假定独立同分布于在零出截尾的正态分布 。其中,mit=zitδ,zit是一个影响企业的效率的p*1的变量向量,δ是一个1*p的待估参数向量。在具体的估计过程中,仍采用和BC(1992)模型一样的格点搜索法、循环迭代法等。需要指出的是BC(1992)和BC(1995)是不可互推的两类模型。
由于没有完善的理论指导本文选择何种变量作为解释影响技术非效率的因素,现有研究在变量选取上具有主观随意性。因此在不进行影响因素分析的前提下,本文拟采用BC(1992)模型进行实证分析。
(二)模型选择
随机前沿分析(SFA)与数据包络分析(DEA)分别是参数法和非参数法中主流的拆解全要素生产率的方法。二者的使用都非常广泛且一些学者认为二者测度出的数据比较相近。考虑到适用性和优缺点,本文认为随机前沿法在分析区域农业全要素生产率时要比数据包络分析更加适合。理由如下:一是因为要研究江苏省区域农业全要素生产率,现有的统计数据是一个多投入单产出的系统,随机前沿分析法可以适用。二是江苏省内地区间经济体量、发展程度、速度和结构差异较大,各个县(市)在农业发展上必然存在较大的差异,因此不适合共用同一生产前沿面。此外,考虑到统计误差和异常值,SFA比DEA更加适用。三是为了进一步分解农业全要素生产率增长,并且考虑到影响农业生产的随机误差项(气候条件、自然灾害等),需要对随机误差和技术非效率项加以区分,因此SFA更加适用。
(三)全要素生产率增长的分解方法
分解得出的技术效率为进一步分解全要素生产率中的其他成分提供了可能。根据Kumbhakar[2]的研究,在随机前沿生产函数模型的基础上,在多要素投入产出条件下,可以将全要素生产率的变化分解为技术进步、技术效率的变化、规模经济性和配置效率四个部分。
暂时不考虑计量模型中的随机误差项,xit、yit分别表示投入和产出,用时间t测度技术进步,技术损失项非负且时变。
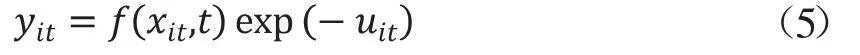
T表示数据的最大期数,ui的概率分布同上,依然是截尾正态分布,η为待估参数。
对式(5)左右两端取对数并对时间求导得到:
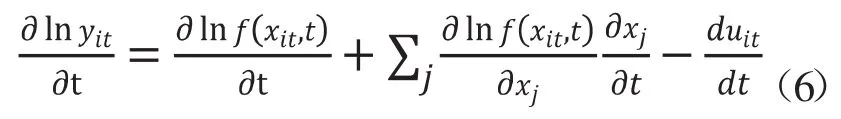
将求导结果中的近似看作要素的弹性为要素随时间的变化率,记为为技术效率变化。令投入要素的产出弹性之和为RTS,RTS也被称作规模报酬指数,要素在前沿生产函数中的相对产出弹性。由此全要素生产率增长被分解为:
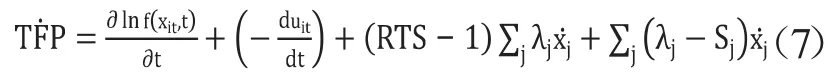
其中, 表示第j个投入要素在总要素总所占的比重, ,RTS通过与1的比较可以显示出规模报酬的情况,于是全要素生产率TFP的变化率被最终分解为四个部分:
技术进步(TP)。,表示在技术进步作用下生产前沿面,或者说生产的可能性边界的移动。
技术效率变化(TE),表示在既定的技术条件下,实际产出和理论上的前沿面之间的差距随时间变化的程度,当技术效率改进时,反映实际生产水平对技术最大可能面的追赶速度。
规模经济性,表示其他条件不变时,改变要素投入规模引起的产出变动。
配置效率(AE)。,将要素的弹性作为投入要素数量比例是否合理的一个评价维度,表示实际要素投入的比例结构对与合理比例偏离的改进速度。
三、SFA实证分析及TFP增长分解结果
(一)数据来源
本文选取苏北和苏中地区32个县及县级市2010-2015年的县级农林牧渔业生产投入产出面板数据,采用随机前沿法和超越对数生产函数对江苏省农业主产区进行建模分析。所采用的各类总量指标数据来自2011-2016年《江苏统计年鉴》《江苏省农村统计年鉴》和《全国统计年鉴》,具体的县(市)选取见表1。

表1 研究县(市)选择
需要说明的是,由于一些地区在2010-2015年间行政区划发生了变化,因撤县改区,连云港市的赣榆县划归连云港市赣榆区,扬州市江都市划归为扬州市江都区,泰州市姜堰市划归为泰州市姜堰区等。因此,本文以2015年年末最新的江苏省行政区划为准,在实证研究中删去上述县(市)。
任何单位进行生产都需要两种基本的投入要素:劳动力和资本。在农业生产的研究中,土地、农业机械和化肥可以理解为特殊的资本投入,本文的投入产出要素见表2。

表2 投入产出要素表
(二)模型基本设定
相比于一般的柯布道格拉斯生产函数,超越对数生产函数加入了投入要素的平方项,相互之间的交叉项,具有易估性和包容性等特点。在本文的随机前沿分析应用中,由于县(市)数量较多,可以满足使用超越对数生产函数的条件。
本文中计量模型设定为超越对数形式的随机前沿生产函数模型,具体形式为:
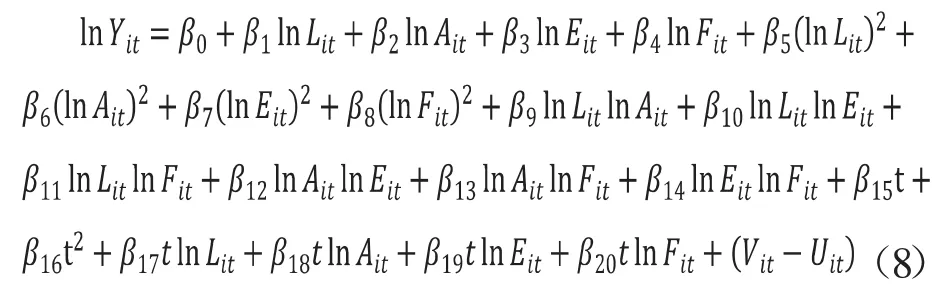
其中,β0~β20均为待估参数,i表示江苏省苏北和苏中地区32个县及县级市,t表示年份(2010-2015年),其中Yit表示农林牧渔业总产值(亿元),Lit表示农林牧渔业从业人员(万人),Ait农作物总播种面积(千公顷),Eit表示农业机械总动力(万千瓦),Fit表示农用化肥使用量(万吨),t为时间趋势变量,反映农业及生产的技术进步作用为均值为零的正态分布扰动项,Uit为非负项,衡量地级市的效率损失水平,,服从零点左侧截断的断尾正态分布,该项符合时变模型的具体形式。
(三)SFA实证分析结果
通过STATA进行随机前沿分析估计模型(7),结果如表3所示。
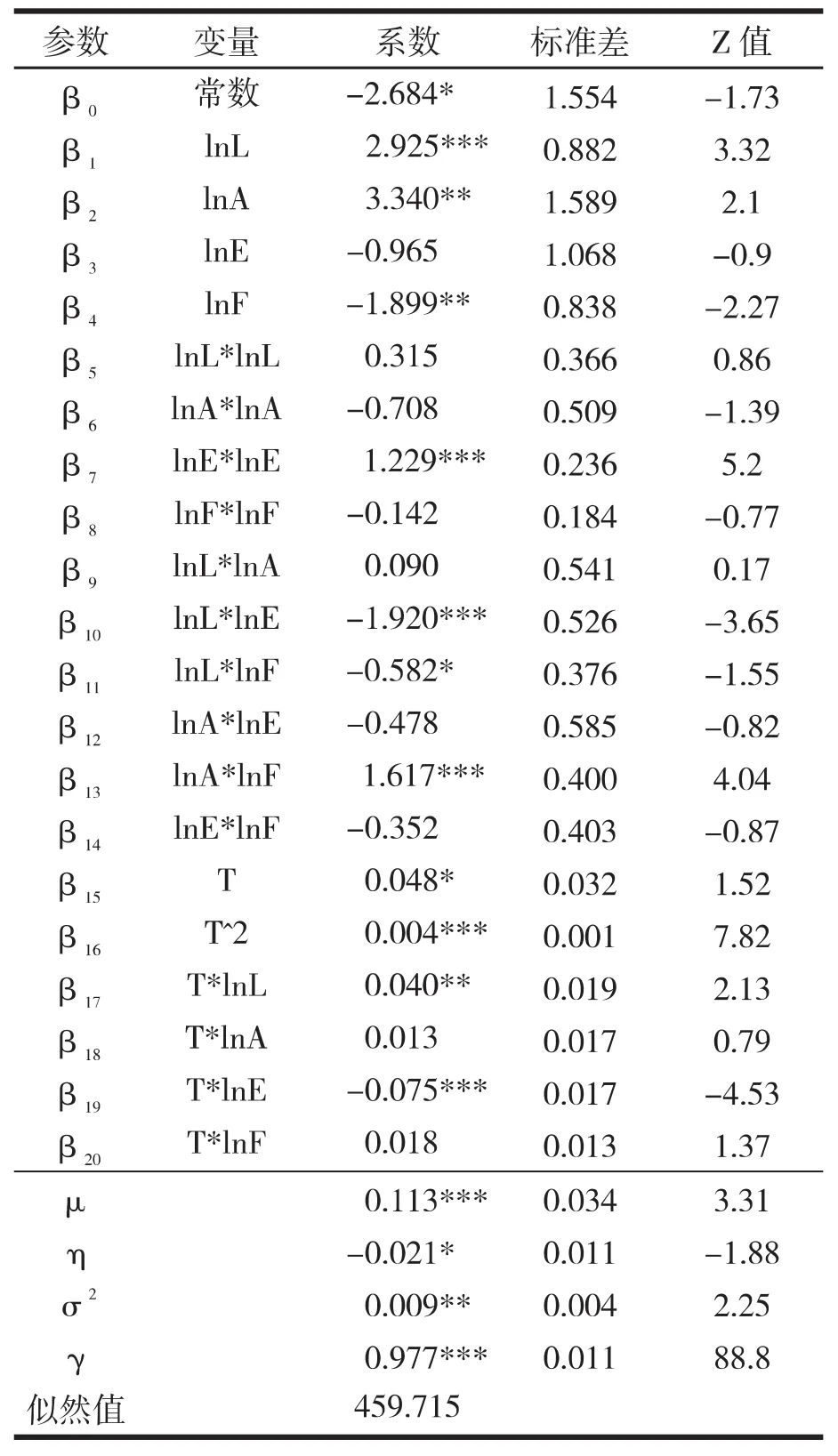
表3 随机前沿法最大似然参数估计结果
由表3可知,江苏省32县(市)的农业生产模型中,大部分的参数都通过了Z检验,说明此模型具有良好的解释效果。首先反映了实际产出对技术前沿面的偏离中技术非效率项的重要程度,为97.7%,说明实际产出偏离的差距大部分来自于生产的效率损失,随机误差的作用占不到3%,且γ在1%的条件下显著不为零,因此,本文使用随机前沿生产函数是合理的。
μ值为 中截尾正态分布的均值,它在1%的概率下显著不为零,说明Uit的分布相对于标准正态分布显著右偏,选用截尾正态分布假设是合理的。而时变系数η的值在10%的概率下显著不为零,说明模型中的技术非效率项Uit确实随时间发生变化。此外,η值绝对值偏小且为负,说明在2010-2015年的六年间技术效率的损失变化较小,并且呈递增趋势。因此,本文选用时变模型也是合理的。
根据表 3的模拟结果,lnL*lnE、lnL*lnF、lnA*lnE、lnE*lnF项的系数都是负值,说明劳动力和农用机械、劳动力和化肥施用量、土地和农用机械,农用机械和化肥施用量的交互作用是相反的。其中,lnL*lnE、lnL*lnF的系数通过了显著性检验,说明劳动力投入和农用机械,劳动投入和化肥施用量是呈互为替代的关系。尤其是劳动力和农用机械这一对投入,它们之间的替代关系正契合了农业经济学中对于农业发展路径的论述——当劳动力稀缺时,农业倾向于发展依赖农用机械代替人力的规模性农业;相反,当劳动力过剩时,则会发展提高单产的集约型农业技术,符合经济学规律。此外,lnL*lnA、lnA*lnF交叉项的系数都是正值,说明了劳动力和土地、土地和化肥施用量具有互补效应。其中,lnA*lnF项的系数通过了显著性检验,这意味着同等条件下,越多的土地投入需要更多的化肥施用,这也与经济学规律相契合。
根据模拟结果的系数可以进行投入要素的弹性计算。在2010-2015年之间,劳动力投入和农机投入的平均产出弹性都呈负值,而土地投入和化肥投入的平均产出弹性则呈正值。
土地的投入产出弹性为0.732,说明土地仍然是制约农业生产的最重要投入要素。其中,土地投入产出弹性最大的是灌云县(1.157),最小的为仪征市(0.271)。说明只要集约使用农业用地,江苏省农业主产区仍然能继续增产,土地使用还处在具有规模报酬的阶段。
农用机械总动力的平均产出弹性为-0.072,说明总体上江苏省存在农业机械动力投入过剩的现象。各个地区的农业机械动力投入产出弹性差别很大,有11个县(市)农机投入的产出弹性为正值。这表明研究地区在农业机械设备的配置上不均,存在改进配置效率的空间。
农用化肥施用量的平均产出弹性为0.112,表明研究地区可能总体上呈现化肥投入不足的现象。而各县(市)在这一指标上差别较大。考虑到农业污染越来越严重的情况,是否需要增加化肥施用量有待商榷。
(四)农业生产技术效率估计结果
在估计出随机前沿生产函数模型的同时,还可以得到不同县(市)的技术效率损失项Ui的值,根据时变模型的公式:
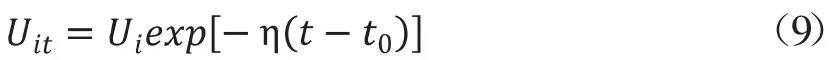
可以计算出不同地区不同年份的技术效率损失项Uit的值。
在此基础上,根据公式:
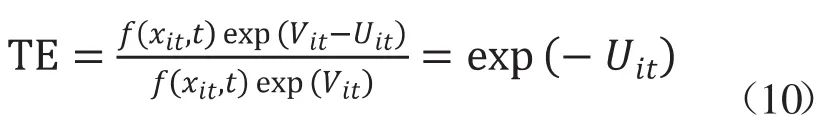
可以推算出各地区的生产效率的大小,即技术的有效程度。为了更加清晰地对比各个地区间农业生产效率水平的差异,本文对所有32个县(市)在2011-2015年间的技术效率水平进行K均值聚类分析。聚类的结果如表4所示。聚类结果显示,所有县(市)被分为三类。
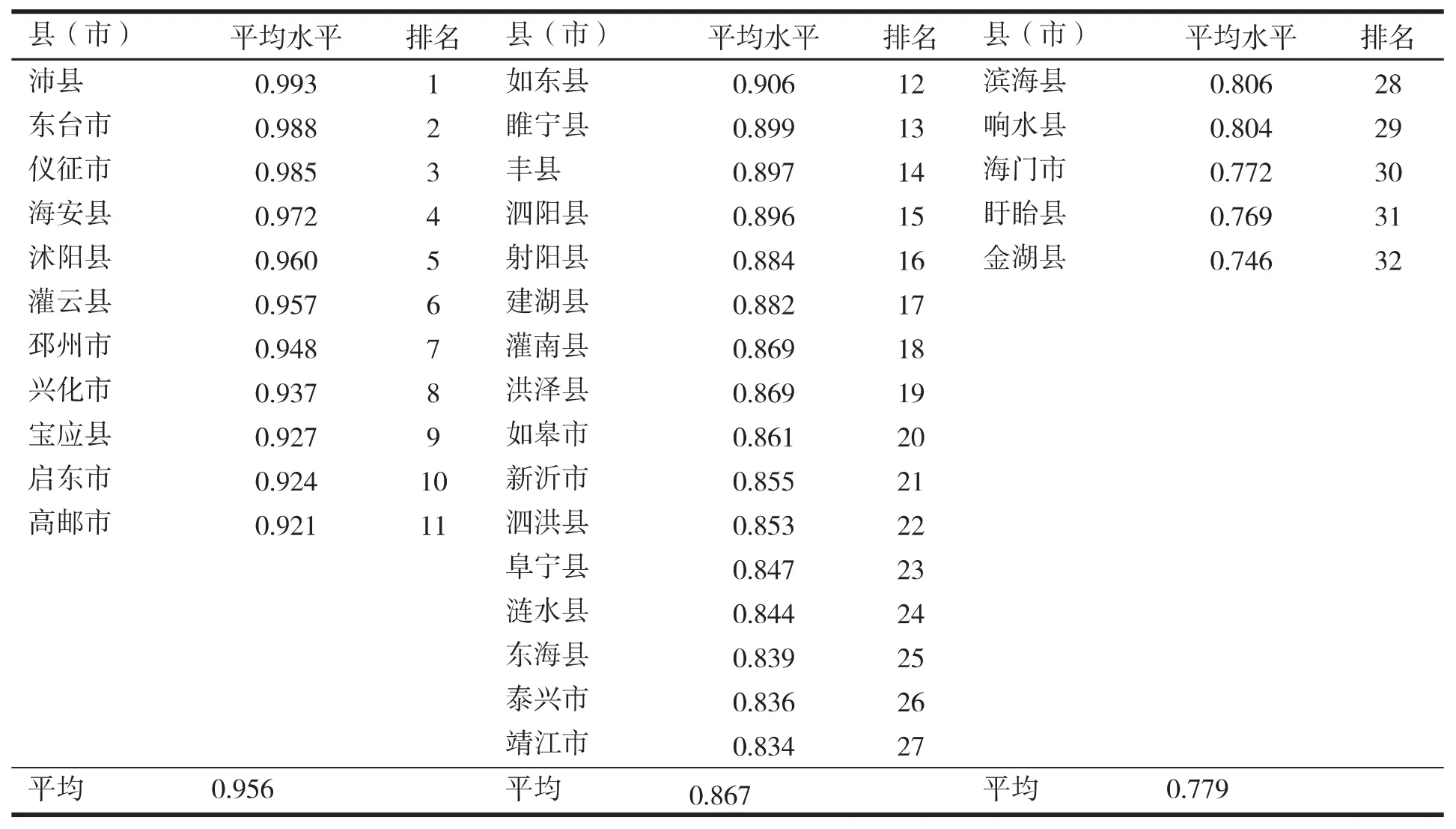
表4 各县(市)农业生产技术效率水平聚类结果
由表4可知,江苏省苏北苏中地区的县域农业组织水平较高,2010-2016年间全部地区的平均生产技术效率水平达到88.3%。其中,沛县农业生产的平均技术效率水平最高,达99.3%,金湖县最低,为 74.4%。受限于模型的原始假定和估算结果,时变系数 η=-0.021,小于零,说明在该期间地区整体的技术效率水平呈下降趋势,下降幅度较小,地区整体平均降幅仅为 1.1%。
3)数据输出:土地变更调查记录表示土地利用变更调查的主要成果,系统可将变更前后的图斑号、面积等属性信息以及图斑截图内容自动写入记录表中,进而可为年度土地利用变化情况的分析报告提供高精确度的数据信息。
(五)农业全要素增长分解分析
代入具体的函数形式和投入要素,可得技术进步(TP)为:
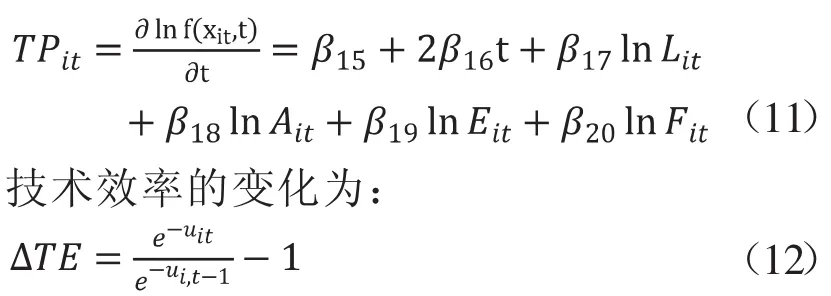
投入要素中劳动力(L)、播种面积(A)、农业机械总动力(E)和化肥施用量(F)的投入产出弹性分别为:
规模报酬指数为要素弹性之和,为:
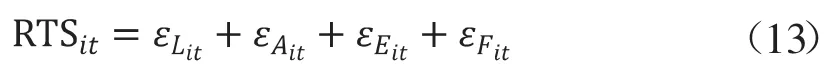
可以推导出要素的相对产出弹性,分别为:
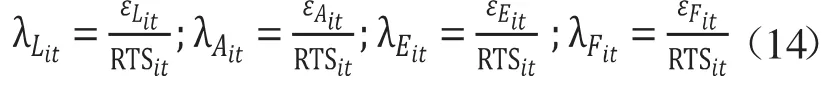
则规模经济性为:
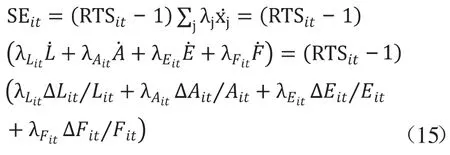
要素的配置效率为:
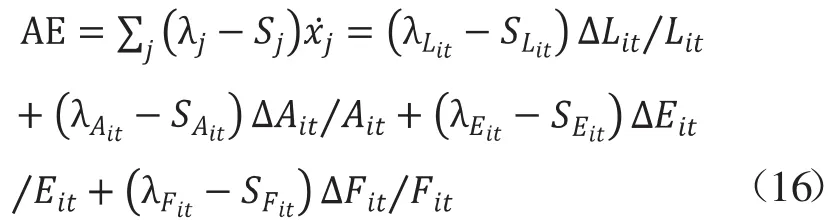
根据上述公式,代入具体的数据,计算可得分解结果,根据年份计算平均值后,结果如表5所示。
需要指出的是,在实证分析部分所使用的数据是2010-2015年间的,在分解部分中,公式中有增长率等需要与前一年做差分的项,因此第一年(2010年)的分解数据缺失。分解部分所得出的结果均是2011-2015年间的分解结果,对应我国经济计划正好是“十二五”期间。
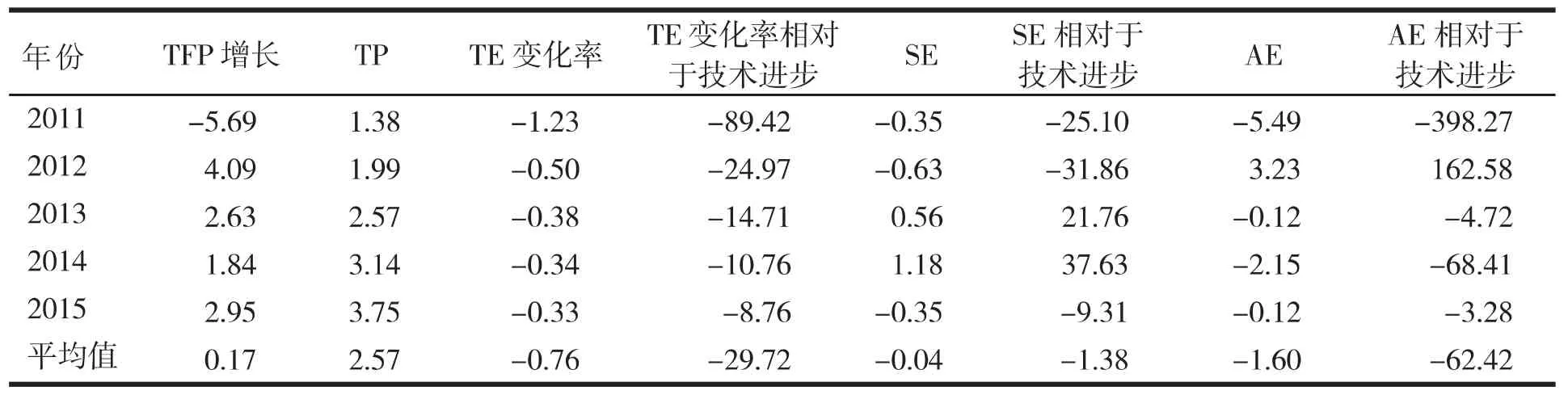
表5 江苏省农业主产区(32个县(市))TFP增长分解结果 单位:%
由于TFP增长率并不全是正值,并且技术进步都是正值,且和TE增长率、SE、AE的绝对值差距不大,本文以TP为计算比例的基准,可以得到各个分解成分相对于TP的大小。即是计算在技术持续进步的前提下,技术效率变化率、规模经济性和配置效率水平相对于技术进步,对全要素生产率增长的贡献(抑制)程度。
由表5可以得出,TFP的增长速度除了在2011年为负值外,其余皆为正值,其平均值为0.17%,说明江苏省农业主产区在“十二五”期间农业生产的全要素生产率总体呈稳步增长的态势,农业生产的效率持续改进。在“十二五”期间,技术进步一直稳定为正,年均技术进步达到2.57%,对研究地区农业全要素生产率增长起到稳定的推动作用,因此技术进步是构成32个县(市)持续改善农业生产效率的主要原因。然而,技术效率变化率对于农业全要素生产率增长具有负效应。技术效率呈缓慢减少趋势,技术的利用水平下降,技术效率变化率必然为负。技术效率变化率在“十二五”期间的均值为-0.76%,相对于技术水平的进步,其抑制程度为-29.72%。此外,规模经济性对农业全要素生产率增长也具有负效应,年均规模经济性为-0.04%,相对于技术进步,年均抑制程度为-1.38%,总体上相对于其他分解部分的作用力而言,规模经济性起到的作用是次要的。在配置效率方面,它对农业全要素生产率增长也是有负效应的,年均配置效率为-1.6%,相对于技术进步,抑制作用达到-62.42%,在四个分解成分中是给全要素生产率增长带来最多负效应的成分,是制约江苏省全要素生产率增加,优化农业生产效率的主要原因。
为了更加清楚地反映地区间农业全要素生产率增长和其分解成分之间的综合水平差异,本文对江苏省苏北和苏中32个县(市)在“十二五”期间的综合结果进行了聚类分析。从函数角度说,技术效率变化率本身只是技术效率的导数,反映了技术效率的变化方向和程度,因此,本文在聚类分析的时候加入技术效率的原始数值。参与聚类的变量分别为,技术进步(TP)、规模经济性(SE)、配置效率(AE)、技术效率变化率和技术效率(TE)。
从表6可知,第一类地区只有沭阳县。其农业全要素生产率增长的综合水平为3.94,同时技术效率水平也较高,达到96。这表示沭阳县在“十二五”期间,在优化农业生产效率、提高农业全要素生产率方面是最突出的。
第二类地区以宝应县、东台市、丰县、高邮市、灌云县、海安县、建湖县、沛县、邳州市、启东市、如东县、射阳县、泗阳县、睢宁县、兴化市和仪征市等16个市(县)为代表。平均农业全要素生产率增长率为 1.41,平均技术进步为 2.72,平均规模经济性为 0.8,平均配置效率为-1.96,平均技术效率变化率为-0.15,平均技术效率为 93.15。第二类地区在农业生产效率水平优化速率上整体处于中游水准,在各方面还有较大的改进空间。
第三类地区以滨海县、东海县、阜宁县、灌南县、海门市、洪泽县、靖江市、金湖县、涟水县、如皋市、泗洪县、泰兴市、响水县、新沂市和盱眙县等15个县(市)为代表,它们的平均农业全要素生产率增长率仅为1.19,低于第二类地区的同类指标。第三类地区平均技术进步为2.43,平均规模经济性为0.49,平均配置效率为-0.35,平均技术效率变化率为-0.41,平均技术效率仅有82.54。相比较而言,第三类地区在“十二五”期间的生产效率优化方面,即农业全要素生产率增长水平最低。相对较慢的生产效率进步水平和较低的技术效率水平制约了第三类地区的可持续发展势头。
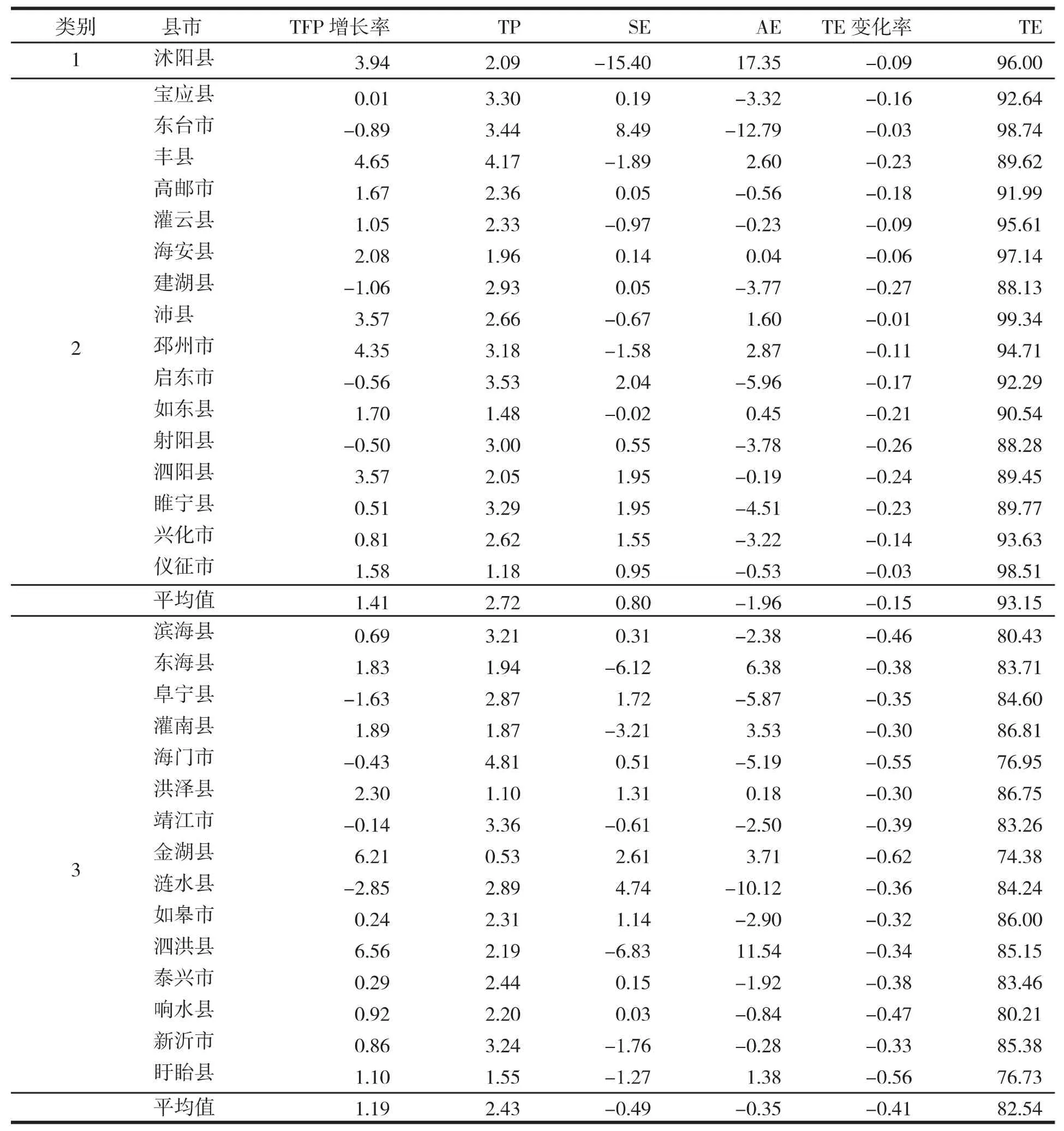
表6 对各县(市)TFP增长及其分解成份综合表现聚类结果 单位:%
四、结论与建议
(一)技术进步构成推动农业生产效率改善的最主要原因
根据分解模型得到的结果,“十二五”期间,32个县(市)的农业全要素生产率保持增长的势头,年均增长0.17。排除“十二五”第一年的较大波动外,平均增幅2.88。这样的增长势头很大程度上来自于技术的持续进步。同时期,研究地区技术进步年均稳定增长2.57,且进步速度年年攀升,2015 年末达 3.75。在“十二五”期间,我国加快推进农业现代化进程,农业科技进步贡献率达到56%①农业部关于印发《“十三五”农业科技发展规划》的通知,2017。。显然,江苏省苏北苏中地区在贯彻落实中央对农业技术发展的要求方面做出了积极的响应。
(二)农业生产资料配置效率是制约农业生产效率改善的主要原因
配置效率是在四个分解成分中给全要素生产率增长带来最多负效应的成分,年均配置效率为-1.6,相对于技术进步,抑制作用达到-62.42,是制约江苏省全要素生产率增加,优化农业生产效率的主要原因。配置效率的变化趋势和全要素生产率增长的变化趋势十分相似,在技术进步、技术效率变化率和规模经济性在“十二五”期间相对稳定的条件下,配置效率是引起全要素生产率增长波动的最主要成分。
因此,为了提高生产资料的配置效率,要继续改革农村土地使用制度,有序引导农村剩余劳动力转移,提高农业机械、农业生物技术在生产过程中的应用水平,减轻资源错配对提升生产效率的抑制作用。
(三)农业技术效率水平稳定高企,但部分地区仍有较大改进空间
根据随机前沿模型对技术效率的估计结果,江苏省内32个县(市)的平均技术效率水平达到88.3,并在“十二五”期间有缓慢的下降趋势,平均降幅为1.1。根据聚类分析结果,仍然有不少县(市)的技术效率水平相对较低,滨海县、响水县、海门市、盱眙县和金湖县的平均技术效率水平仅有77.9,仍然存在改进的空间和必要。
(四)农业生产规模经济性是制约农业生产效率改善的次要原因
根据分解结果,研究地区在“十二五”期间的规模经济性方面维持了平稳的态势,年均值为-0.04,在农业全要素生产率增长分解成分中占比较小,是制约生产效率改善的次要原因。同一时期,江苏省农业生产规模报酬指数(RTS)平均值为0.715。这反映了江苏省农业主产区的规模经济性为负的原因很可能来自于农业生产整体体量过大,不符合产业结构安排的比较优势。这也和苏北苏中地区为江苏省包括粮食在内的所有主要农产品的主产区,农业在产业结构中占比重较高等事实相吻合。
(五)提高农业生产效率的主要建议
1.持续投资科技创新,坚持科技进步对提升生产效率的主导作用。主要手段有:调整科技发展的方向。从注重粮食科技,向粮食、经济作物、饲料统筹发展转变。从注重农业种植技术改进,向注重资源调配、种植技术和环境保护的全过程转变;扩大农业科技人才队伍。为了农业科技多元化的发展方向,加快农业科技产品的研发速度,要加大政策扶持力度,促进农业企业的技术创新能力。重点培养以农民为主体的农业技术应用人才,加快农业人口向职业农民转变的速度。
2.优化投入要素结构,减轻资源错配对提升生产效率的抑制作用。资源错配、要素误置可能来源于部分要素的流动、增减机制不畅。因此,首先是要继续改革农村土地使用制度。在依法、有序推进土地经营权流转,实现规模经营、合理使用农业机械的同时,稳定农村土地承包关系,为培育新型农业经营主体和培养新型职业农民打下土地制度基础。其次要有序引导农村剩余劳动力转移。在苏北和苏中这样就全国而言经济水平相对较好的地区,应当以农民为主,发挥农民积极主动性建设农村小城镇,利用诱致性转移代替强制性转移,因地制宜发展农村非农产业,也为异地转移的返乡农民回乡就业提供了可能性。
3.发掘技术效率潜力,改善科技应用水平以提升生产效率。江苏省农业主产区的部分地区仍然存在较多的农业技术效率提升空间,然而近年来技术效率有缓慢的下降趋势。通常认为技术效率和地方经济发展水平,市场条件、自然灾害程度等因素有关。而改善技术效率最具有操作性的方法,就是提高农业科技的推广水平。要建立完善的农业技术推广体系。为了适应农业信息化、规模化的需要,建立以国家农技推广机构为主,农民合作组织、涉农企业、农业科研和教学机构为辅的“一主多元”的农业技术推广体系。要引导赢利性、经营性组织开展农技推广服务。通过定向委托、招标投标等方式鼓励专业服务组织、农业技术协会、涉农企业参与到农业的产前、产中、产后服务过程中来。
[1]Romer D,Chow C.Advanced macroeconomic theory[M].Mcgraw-hill,1996.
[2]Kumbhakar SC,Denny M,Fuss M.Estimation and decomposition of productivity change when production is not efficient:a paneldata approach [J].Econometric Reviews,2000,19(4):312-320.
[3]Battese G E,CorraGS.Estimation ofa production frontier model:with application to the pastoral zone of Eastern Australia[J].Australian Journal of Agricultural and Resource Economics,1977,21(3):169-179.
[4]Fare R, Grosskopf S,Lovell C A K.Production frontiers[M].Cambridge University Press,1994.
[5]吴清华,李谷成,周晓时,冯中朝.基础设施、农业区位与种植业结构调整——基于1995—2013年省际面板数据的实证[J].农业技术经济,2015,(03):25-32.
[6]余康,等.1989-2009中国总量农业全要素生产率研究综述[J].浙江农林大学学报,2012,(01):111-118.
[7]尹朝静,李谷成,葛静芳.粮食安全:气候变化与粮食生产率增长——基于HP滤波和序列DEA方法的实证分析[J].资源科学,2016,(04):665-675.
[8]Battese G E,Coelli T J.Frontier production functions,technical efficiency and panel data:with application to paddy farmers in India[M].International applications of productivity and efficiency analysis.Springer Netherlands,1992:149-165.
[9]Battese G E,CoelliT J.Amodel for technical inefficiency effects in a stochastic frontier production function forpaneldata[J].Empiricaleconomics,1995,20(2):325-332.

