硅片自旋转磨削中基于力的微接触机理

任庆磊，魏 昕，谢小柱，胡 伟

(广东工业大学 机电工程学院，广州 510006)

0 引 言

目前，绝大多数的集成电路(IC)芯片的衬底材料都采用单晶硅片，而单晶硅片的质量直接决定芯片的性能和成品率[1]。传统的硅片加工多采用研磨、腐蚀等工艺，但加工效率低，尤其对大直径(φ≥300 mm)硅片的加工，而采用超精密磨削加工会比传统加工效益更优，其中应采用杯型金刚石砂轮进行硅片自旋转磨削是典型的硅片超精密磨削加工形式[2]。采用杯型金刚石砂轮进行硅片自旋转磨削加工的方式是由日本学者Matsui首先提出[3]，硅片在真空作用下吸附在旋转工作台上，硅片的直径略小于旋转工作台的直径，两者的中心重合。调整砂轮内外沿(工作面)的中心轴线，使其与硅片中心对齐。磨削加工中，砂轮与硅片都绕各自的中心轴线旋转，砂轮只做轴向进给运动。这种自旋转磨削方式可通过调节硅片转速与砂轮轴向进给速度来控制磨削深度，从而可实现以塑性去除方式的延性域磨削。

在硅片自旋转磨削加工的应用过程中，其磨削加工机理是研究的重点，备受国内外研究学者关注[4]。其中，国外代表性的是Pei等[5]通过改变加工的多因素参数进行了一系列磨削试验，系统研究了磨削加工工艺对硅片表面质量的各种影响。国内代表性的是康仁科等为获得高质量超薄硅片进行了大量自旋转磨削工艺试验研究[6]。这些研究为获得直观的高质量硅片偏重于试验性。而对硅片自旋转磨削加工机理的理论性研究主要集中在硅片材料去除机理方面，包括以“压痕断裂模型”为基础的脆性去除机理及延性域的塑性去除机理[7]，这些机理研究的工作是采用压痕和划痕试验构建经验公式的形式找出硅片的材料去除规律，但由于其磨削过程的复杂性，磨削加工机理研究仍未形成统一的认识。同时，硅片材料去除机理研究所依托的微观模型主要是磨粒与硅片间的两体模型，侧重于对磨削中硅片的微观影响研究，欠缺对磨削中砂轮的微观影响研究[8]。

基于此，本文从稳定延性域磨削过程中抽取出砂轮微单元与硅片的微接触作为研究对象，提出并建立了微观三体力学模型，应用力分解法对自旋转磨削过程中砂轮与硅片的微观相互作用机理进行了理论分析研究，为硅片自旋转磨削中硅片材料去除机理及砂轮磨损研究提供相关理论支撑。

1 力学模型

为建立三体力学模型，在硅片自旋转稳定磨削过程中，从砂轮与硅片的接触加工区域中提取出包含单颗磨粒的砂轮微单元作为研究对象。提取过程是从宏观砂轮端面上取包含单颗磨粒的结合剂，如图1所示，由一定体积的结合剂把持单颗金刚石磨粒组成。结合剂的体积由砂轮浓度、磨粒半径R及金刚石密度决定。这里假定：宏观砂轮的端面结合剂是均实平整的；宏观砂轮中金刚石微粉磨粒分布是均匀的，形状为球形，出刃高度为粒径的三分之一。

图1 砂轮微单元的提取Fig.1 Extraction of wheel micro unit

提取出的砂轮微单元与硅片在延性域磨削中产生微接触。砂轮微单元与硅片微接触的理想力学模型如图2所示，其中，Az为法向接触面积；Ax为切向接触面积。这里假定延性域去除的硅材料是塑性的。

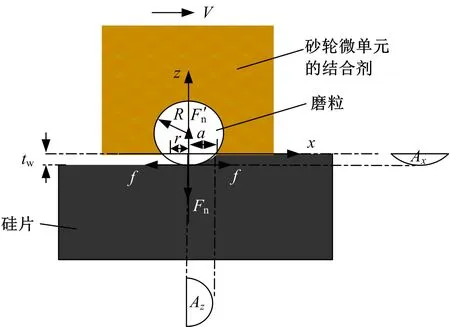
图2 微接触力学模型Fig.2 Micro contact mechanics model

2 计算及分析

2.1 法向弹性接触

分解的法向上，切深较小时，接触处于弹性阶段，接触区域为圆形，根据接触力学中赫兹理论[9]公式，可求得接触圆的半径a、对应切深的接触深度tw和接触中心点的最大压应力p0，公式如下：

(1)

(2)

(3)

砂轮微单元与硅片接触达到弹性接触极限时，其临界点就是最大接触压应力p0达到硅的屈服强度Y，根据式(1)～(3)可求出砂轮微单元与硅片接触时超出硅片弹性接触范围的临界法向载荷、临界切深及临界接触圆半径。

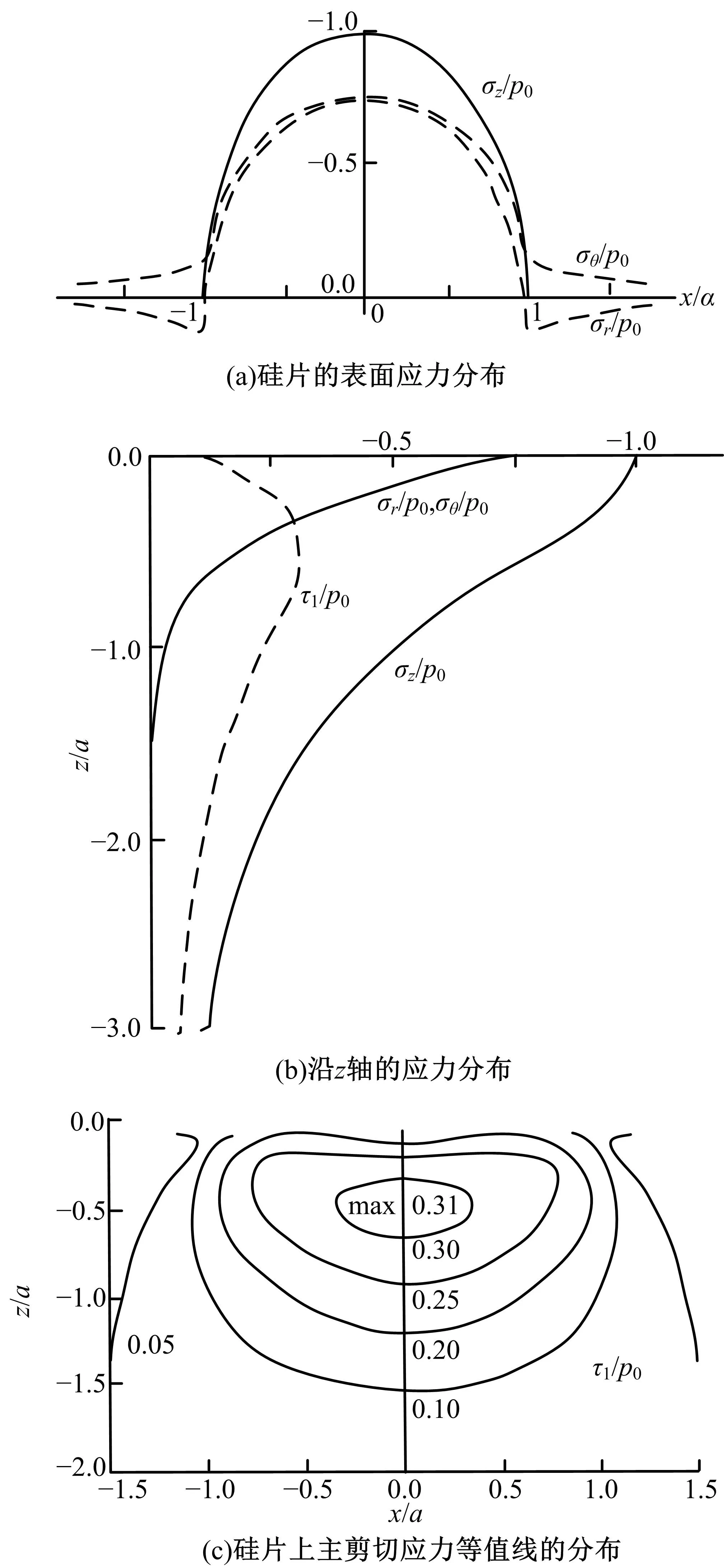
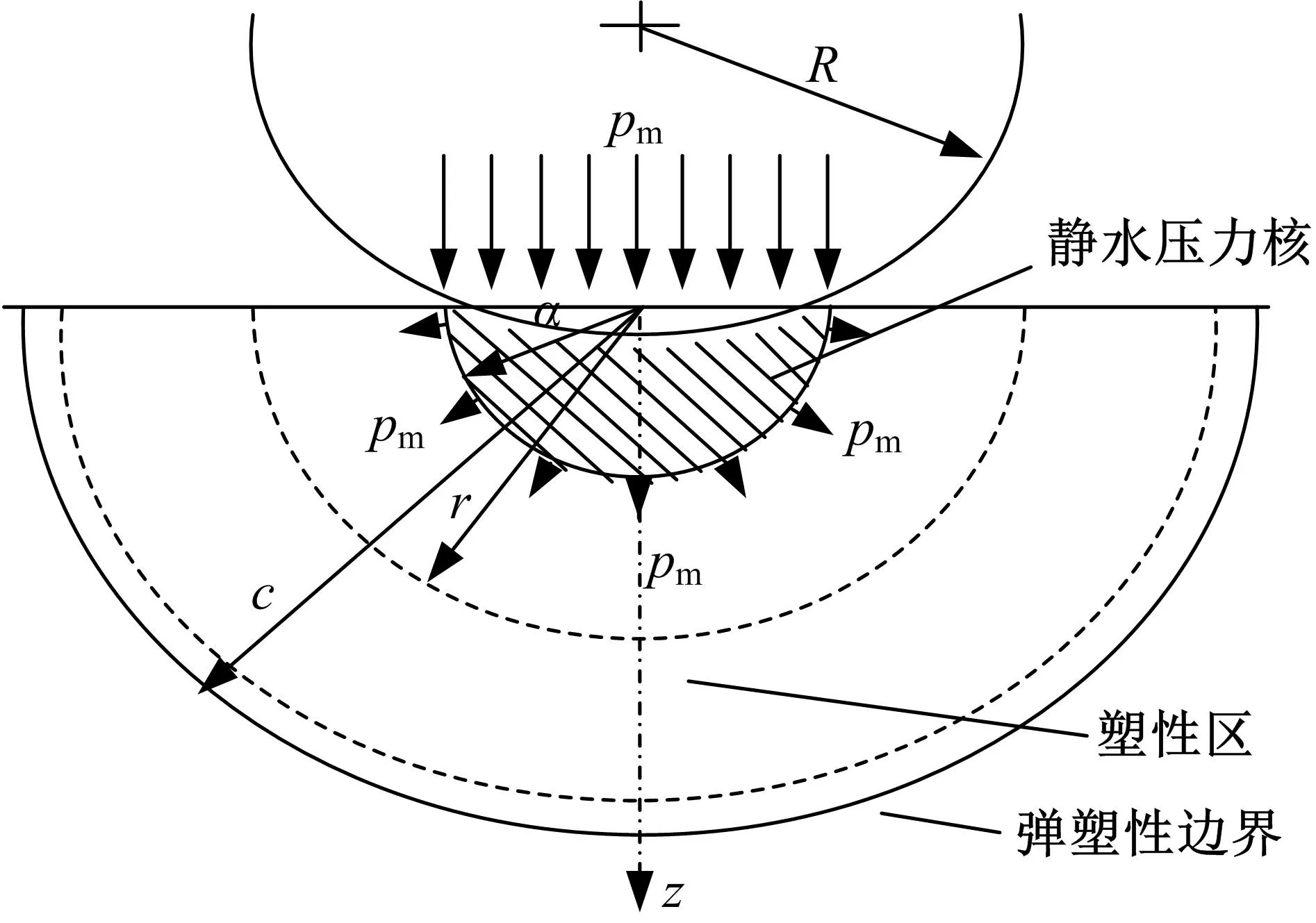
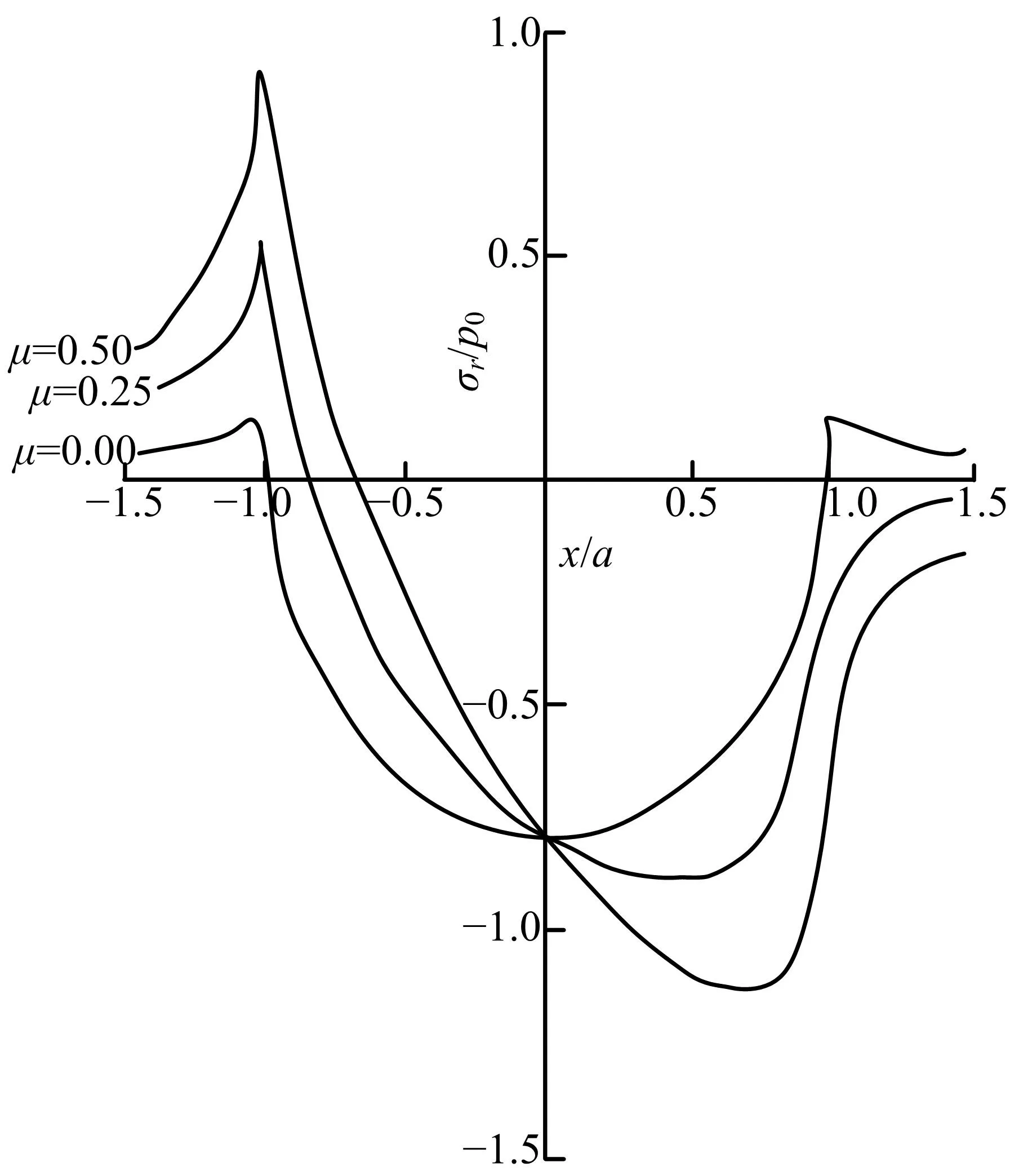
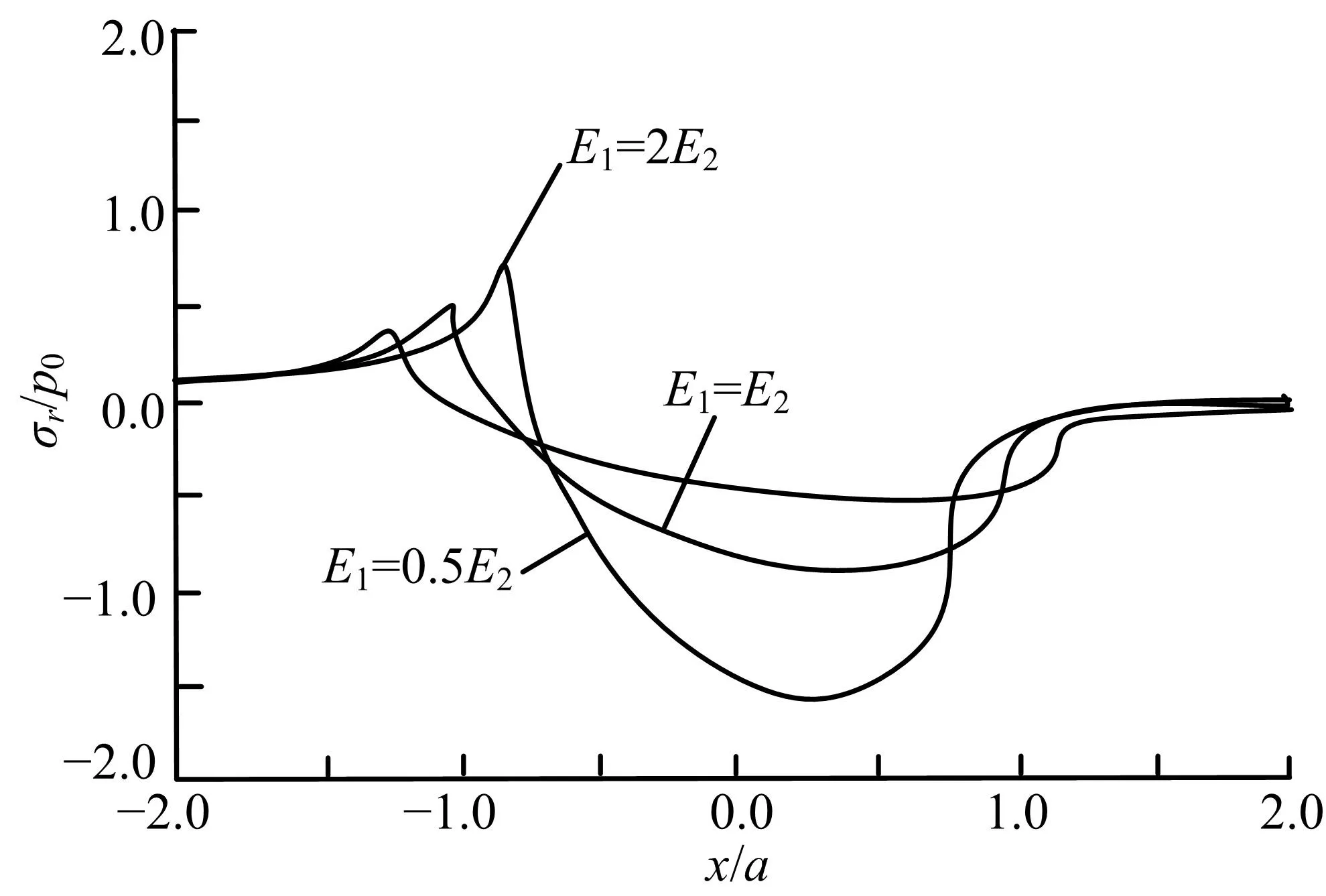
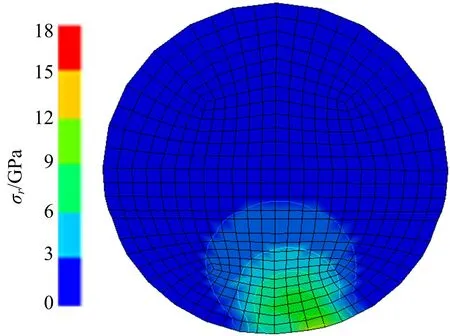
法向载荷接触处于弹性阶段的应力场情况同样依据接触力学的赫兹理论[9]来得到。如图3所示，在接触圆内(r

(4)

图3 弹性阶段的应力分析Fig.3 Stress analysis in elastic phase

在接触圆外(r>a),z=0的硅片表面应力场的极坐标表达式为：

(5)

在硅片表面以下(z<0)沿z轴的应力分布可认为是在半径r上的环形集中力，即：

(6)

同时，主剪切应力τ1的分布可以表示为：

τ1=0.5|σz-σr|

(7)

由式(4)～(10)可得出接触硅片在弹性接触阶段的应力分布情况如图4所示。

图4 弹性接触阶段接触硅片的应力分布Fig.4 Stress distribution of contact with silicon wafer during elastic contact phase

法向载荷反作用到砂轮微单元上可看成是以结合剂为基体、金刚石磨粒为表层的双层体受法向力作用的情形，如图5所示。根据多层体上的接触力学赫兹理论[9]，可对砂轮微单元进行载荷应力分析。双层体接触力学分析过程中，设定表层的弹性模量E1对应砂轮微单元中金刚石磨粒的弹性模量ED，表层的厚度为h，对应磨粒的直径2R；基体的弹性模量E2对应砂轮微单元中结合剂的弹性模量EJ，接触半径为a。

图5 砂轮微单元受载荷看作双层体接触受力示意图Fig.5 Contact force diagram of wheel micro unit load as double body

根据双层体弹性接触理论分析结果给出不同E1/E2比值下砂轮微单元等效的应力分布情况，如图6所示。

图6 弹性接触阶段砂轮微单元等效应力分布Fig.6 Elastic contact stage grinding wheel micro unit equivalent stress distribution

由图6可以看出：砂轮微单元双层体在接触表面上的应力分布与作用在硅片接触表面的情况相似，只是方向相反，互为作用与反作用力，而接触表面以下由于是双层体，虽正应力分布的趋势仍与硅片上的相似，但由于存在界面，不同的材料特性(弹性模量及泊松比不同)使得剪应力的传递在界面上出现跳跃或不连续性。

2.2 法向塑性接触

分解的法向上，切深tw超过弹性临界切深后，接触开始进入塑性阶段，可根据接触力学[9]的“空腔模型”理论(见图7)来进行分析。硅片产生的内层位移近似成起始于接触点的放射线，它的应变等值线是半球形。在这个简化的塑性接触模型中，磨粒的接触面被包围在半径为a的半球“静水压力核”内，核内有平均接触压力pm，pm不会使硅片产生塑性屈服，但在“静水压力核”之外，塑性流动向周围扩散，塑性应变逐渐变小，直至半径为c处的弹性应变，这是塑性变形的边界，其中c>a。

图7 塑性压入硅片的空腔模型示意图Fig.7 Schematic diagram of cavity model of plastic pressure in silicon wafer

在硅片塑性区a≤r≤c，应力表达式为：

(8)

在硅片弹性区r≥c，应力表达式为：

(9)

在静水压力核的边界上，pm可表达为：

(10)

而塑性变形边界位置的表达式为：

(11)

将式(11)代入式(10)可得半球核内压力表达式为：

(12)

分析式(12)可知，随着磨粒切入尺寸(a/R)的增大，硅片所受的平均压力也逐渐增大，同样法向载荷也随之增大，硅片也会从初始塑性变形逐渐扩展至塑性极限而出现断裂，即当球核内的最大应力达到硅片的脆性破裂强度时，就会出现裂纹。

将硅片的脆性破裂强度代入式(12)可得出对应精磨3000#砂轮(对应的磨粒半径R约为2 μm)的微单元与硅片塑性接触产生半球核半径a的临界值约1.1 μm，临界切深约330 nm，临界法向载荷约45 mN。与单颗金刚石磨粒的硅片压痕试验[10]结果(如图10所示，其压头曲率半径为2 μm)相吻合，也说明本文进行的微接触法向弹性及塑性理论分析是有效的。

图8 不同载荷下单晶硅单次压痕形貌图Fig.8 Monocrystalline silicon single indentation morphology under different load

硅片在受法向载荷作用处于塑性阶段时，砂轮微单元上的应力作用情况与硅片受法向载荷处弹性阶段的分析相似，砂轮微单元仍看作是双层体受载荷作用的情形，只是此阶段的法向载荷变大，由于金刚石磨粒的屈服强度极高，较难出现塑性变形，内部应力分布形式不会变化，只是应力数值会随之增大，结合界面上的剪应力同样会随之增大，这样出现界面破坏的可能性就更高。

2.3 叠加切向接触

宏观滑动摩擦定律为f=μFn，其中μ为滑动摩擦因数，它是与载荷、接触面积、滑动速度等条件无关的恒定量，而在微观滑动接触情况下，滑动摩擦因数就不再是恒定量，根据能量耗散机制，滑动摩擦力f可假设为滑动时剪切粘着点产生的粘着摩擦力fa和变形产生的形变摩擦力fd，即f=fa+fd，这样滑动摩擦因数μ也可看成是粘着摩擦因数μa和形变摩擦因数μd，即μ=μa+μd。 当接触切深较小时，处于弹性接触阶段，滑动摩擦力主要是由滑动中的粘着效应产生，根据粘着摩擦机理理论，粘着摩擦力为：

fa=μaFn=Azτa

(13)

式中：τa为硅片抗剪切强度平均值。

将式(1)(2)代入式(13)，得到粘着摩擦因数为:

(14)

由式(14)可分析出，在弹性接触阶段，滑动摩擦力随着切深及法向载荷的增大是增大的，而其粘着摩擦因数是随之减小的。

切深越过弹性临界后，接触开始进入塑性阶段，此时滑动摩擦力主要是由犁沟形变产生，根据形变摩擦机理理论，形变摩擦力为fd=μdFn。

由塑性半球核模型知，核内有平均接触压力pm，故Fn=pmAz，fd=pmAx，可求得形变摩擦因数为：

(15)

由式(15)可分析出，在塑性接触阶段，滑动摩擦力随着切深及法向载荷的增大是增加的，其形变摩擦因数也是随之增大的。

求出切向上的滑动摩擦力，与法向载荷叠加合成后作用在硅片上，其合成载荷在硅片上产生的应力分布情况与法向载荷作用时相似，仍可采用弹性阶段赫兹理论与塑性阶段空腔模型理论来分析，只是载荷值有所增大，方向有所偏转，应力分布情况与单一法向载荷时类似，如图9所示。

图9 叠加上切向滑动摩擦后硅片应力分布情况Fig.9 Stress distribution of silicon wafer after sliding friction is superimposed

滑动摩擦力作用在砂轮微单元上应力分布的情况与法向载荷作用时的分析相似，仍要把砂轮微单元看作双层体来分析。由于双层体的材料非均质性且存在界面，随着弹性模量比值及摩擦因数的增大，磨粒接触区域的前端出现最大压应力与后端出现最大拉应力的趋势更显著。不同弹性模量比时磨粒接触表面的应力分布如图10所示。

图10 叠加上切向滑动摩擦后磨粒上应力分布情况Fig.10 Stress distribution of grinding grain after tangential sliding friction is superimposed

分析结果与本文作者所做的微接触仿真分析[11]结果中切向滑动时硅片和砂轮微单元上的应力分布趋势相一致，如图11和图12所示，说明本文进行的微接触叠加切向的理论分析是有效的。

图11 硅片上切向滑动仿真的应力云图Fig.11 Stress diagram on silicon wafer during tangential sliding simulation

图12 切向滑动仿真砂轮微单元磨粒上的应力云图Fig.12 Stress diagram on grinding grain of wheel micro unit during tangential sliding simulation

3 结 论

(1)从硅片自旋转稳定延性域磨削过程中抽取出砂轮微单元与硅片的微接触作为研究对象，设定假设条件，提出并建立了微接触的理想三体力学模型。

(2)根据磨削过程，对力学模型中的接触力进行了分解，法向上运用接触力学中的赫兹理论与“空腔模型”理论，将分析获得了硅片上对应弹性和塑性阶段的载荷及应力分布情况，同时也获得了砂轮微单元上相应的应力分布情况。将分析结果与单颗粒金刚石硅片压痕试验结果进行对比，证明分析方法有效。

(3)切向上运用微观摩擦学理论分析得出了滑动摩擦力，叠加合成法向载荷后获得了微接触过程中硅片与砂轮微单元上的应力分布情况。将分析结果与砂轮微单元微接触硅片的仿真结果进行对比，证明分析方法有效。本文的研究结果可对研究硅片自旋转磨削机理提供相关理论支撑。

参考文献：

[1] Markku T, Teruaki M, Veli-Matti A, et al. Handbook of Silicon based MEMS Materials and Technologies[M]. 2nd ed. London:William Andrew,2015.

[2] Pei Z J, Strasbaugh A. Fine grinding of silicon wafers[J]. International Journal of Machine Tools and Manufacture,2001,41(5):659-672.

[3] Matsui S. An experimental study on the grinding of silicon wafer-the wafer rotation grinding method[J]. Bull Japan Soc Prec Eng,1988,22(4):295-300.

[4] Zhou L,Tian Y B,Huang H,et al. A study on the diamond grinding of ultra-thin silicon wafers[J]. Journal of Engineering Manufacture,2012,226(1):66-75.

[5] Pei Z J,Fisher G R, Milind B, et al. A grinding-based manufacturing method for silicon wafers: an experimental investigation[J]. International Journal of Machine Tools & Manufacture,2005,45(10):1140-1151.

[6] 康仁科，田业冰，郭东明，等. 大直径硅片超精密磨削技术的研究与应用现状[J]. 金刚石与磨料磨具工程,2003,136(4):13-18.

Kang Ren-ke,Tian Ye-bing,Guo Dong-ming, et al. Present status of research and application in ultra-precision grinding technology of large-scale silicon wafers[J]. Diamond & Abrasives Engineering,2003,136(4):13-18.

[7] Yan J W,Tooru A,Hirofumi H,et al. Fundamental inverstigation of subsurface damage in single crystalline silicon caused by diamond machining[J]. Precision Engineering,2009,33:378-386.

[8] 霍凤伟. 硅片延性域磨削机理研究[D]. 大连:大连理工大学机械工程学院,2006.

Huo Feng-wei. Study on the mechanism of ductile mode grinding of silicon wafers[D]. Dalian: School of Mechanical Engineering, Dalian University of Technology,2006.

[9] Johnson K L. Contact Mechanics[M]. London:Cambridge University Press,1985.

[10] 张赜文. 单压头曲率半径对单晶硅和氮化碳薄膜径向纳动损伤的影响[D]. 成都:西南交通大学机械工程学院,2010.

Zhang Ze-wen. Effect of equivalent radius of indenter on the radial nanofretting damage of monocrystal silicon and α-CNxfilm[D]. Chengdu: School of Mechanical Engineering,Southwest Jiaotong University,2010.

[11] 任庆磊，魏昕，谢小柱，等. 硅片自旋转磨削中基于作用力的微观接触仿真研究[J]. 金刚石与磨料磨具工程,2016,36(2):19-23.

Ren Qing-lei,Wei Xin,Xie Xiao-zhu, et al. Simulation of micro contact based on interacting force in self rotating grinding of silicon wafer[J]. Diamond & Abrasives Engineering,2016,36(2):19-23.