二阶常微分方程边值问题Green函数的研究
刘 慧
(南京财经大学 应用数学学院,江苏 南京 210023)
常微分方程边值问题是微分方程理论研究中的一个基本问题,其中利用Green函数是研究讨论边值问题的一种重要方法.我们可以利用Green函数将微分方程转化成积分方程,从而应用非线性泛函分析中的不动点定理研究积分方程解的存在性.
本文所求二阶常微分方程边值问题的一般形式为

则边值问题(1)、(2)的解为
(3)
其中G(t,s)则为边值问题(1)、(2)的Green函数.
尽管孙经先给出了Sturm-Liouville两点边值问题的Green函数表达式[1],沈以淡给出了定解问题的常微分方程的Green函数表达式[2],葛渭高给出了非共振条件下边值问题的Green函数表达式[3].但是在许多证明积分方程的解的存在性的文献中并没有给出Green函数的具体算法[4-5].
本文主要研究形如二阶常微分方程(1)在不同边值条件下的Green函数.本文首先研究常微分方程(1)在两点周期边值下的Green函数,主要利用Green函数的性质来求得,可是随着边值条件的增加,利用性质来计算Green函数往往会比较复杂,所以本文在第二部分又研究了常微分方程在多点边值条件下的Green函数的求法,最后给出求Green函数具体实例.
1 二阶常微分方程周期边值问题的Green函数
在本节中我们主要利用性质来给出求Green函数的一般方法.
考虑非线性二阶常微分方程
un(t)+λu(t)=f(t,u(t)).λ>0,t∈[a,b]
(4)
在周期边值条件
u(a)=u(b),u'(a)=u'(b)
(5)
下的Green函数.
定理1 若u(t)∈C2[a,b]是二阶常微分方程边值问题(4)、(5)的解,则
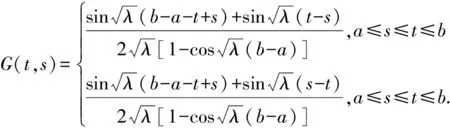
(6)
是边值问题(4)、(5)的Green函数.
证明定理之前先给出Green函数的四条性质[3]:
(i)在a≤t≤b上,G(t,s)本身连续;
(ii)G(t,s)关于t的一阶导数以t=s为第一类间断点且跃度为-1,
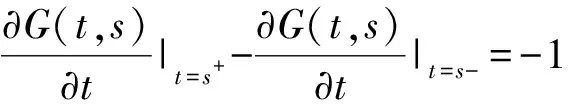
(iii)作为t的函数G(t,s)在[a,s)及(s,b)]上是(1)的解;
(iv)满足边值条件(2).
下面我们将根据Green函数的性质来证明该定理.

应该满足边值条件(5),则有
根据性质(i),可设Green函数的形式如下
(7)
其中α1,α2,β1,β2,为s的待定系数.
设
χk(s)=βk(s)-αk(s),k=1,2
可得到关于χk(s)的线性方程组
即

解得
将α1,α2,β1,β2带入(7)式,整理可得(6).
以上证明过程同时给出了两点周期边值问题Green函数的构造方法.
2 二阶常微分方程多点边值问题的Green函数
随着边值条件的增加,上述方法求Green函数则会比较复杂,本节讨论多点边值问题的Green函数的求法.
定义算子
L:C2[a,b]→C[a,b]
满足
Lu=un+λ1u'+λ2u
(8)
其中λ1,λ2∈C[a,b].U:C[a,b]→Rn.
再定义算子
U:C[a,b]→Rn
满足

(9)
其中ak,(k=0,1,…,m-1)满足
a=a0≤a1≤…≤am-1=b
显然L,U是线性算子.
考虑二阶常微分多点边值问题(8)、(9)在非共振情况下的解.这里我们记
其中u1,u2是u"+λ1u'+λ2u=0的基础解系.
则当detQ(u)≠0,我们称(8)、(9)为非共振边值问题.
定理2 当非线性边值问题(8)、(9)为非共振情况,即detQ(u)≠0,存在唯一的Green函数G(t,s)使(8)、(9)的解为
其中
(10)
证明当detQ(u)≠0设方程Lu=0的基础解系为u1(t),u2(t),记W(t)为Wronsky行列式,显然W(t)≠0,t∈[a,b].有
记
(11)
由常数变易法知方程(8)的一个通解为
带入边值条件(9)中有
即

易知上述G(t,s)满足Green函数的四条性质,换句话说Green函数也可以定义为满足性质(i)-(iv)的函数.[2]
以上证明过程给出了非共振情况下边值问题的的Green函数的构造方法.
3 求Green函数的实例
例1 求:
的Green函数.

应该满足边值条件(13),则有
根据性质(i),可设Green函数的形式如下
(14)
其中α1,α2,β1,β2为s的待定系数.
设
χk(s)=βk(s)-χk(s),k=1,2
可得到关于χk(s)的线性方程组
即

解得
将α1,α2,β1,β2带入(14)式,整理可得BVP(12)、(13)的Green函数为:
例2 求:
的Green函数,其中η∈(0,1),0<βη<1.
证明这里Lu=u",U1(u)=u(0),U2(u)=u(1)-βu(η)
则Lu=0有基础解系
1,t
且相应的Wronsky行列式为

及
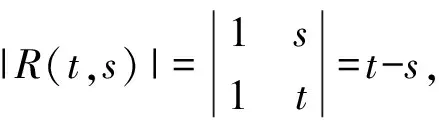
则
故
则 BVP(15)、(16)为非共振的,存在唯一Green函数.
下面分区间讨论其Green函数:
①当0≤t≤η时,
(i)0≤s≤t≤η,
(ii)0≤t≤s≤η,
(iii)0≤t≤η≤s≤1,
②当η≤t≤1时.
(i)0≤s≤η≤t≤1,
(ii)η≤s≤t≤1,
(iii)0≤η≤t≤s≤1,
故BVP(15)、(16)对应的Green函数为
4 总结
(1)在计算Green函数时不管是齐次方程还是非齐次方程,我们只需要考虑求齐次部分的基础解即可.
(2)Green函数的给定和非齐次项t(t)在等式中的位置有关,如果f(t)在等式左方,所求Green函数和我们在本文中所求的Green函数相差一个“-”号.
[参考文献]
[1]孙经先.非线性泛函分析及其应用[M].北京:科学出版社,2008.
[2]葛渭高.非线性常微分方程边值问题[M].北京:科学出版社,2007.
[3]沈以淡.积分方程(第三版)[M].北京:清华大学出版社,2012.
[4]姚庆六.一类奇异二阶边值问题的正周期解[J].数学学报,2007(6):1357-1364.
[5]Sun Jingxian,Liu Yansheng. Multiple Positive Solutions of Singular Third-order Periodic Boundary Value Problem[J].Acta Mathematica Scientia,2005(1):81-88.

