电流频谱可控的单相并网逆变器模型预测控制方法

冀红超,吴文昌，刘永春

(南瑞集团(国网电力科学研究院)有限公司，江苏 南京 211100)

0 引言

近年来，能源危机和环境污染日益加剧，这大大促进了新能源的发展；单相并网技术作为新能源发电并网的关键技术之一，也成为了当前的研究热点。目前，应用于单相并网逆变器的控制策略按照触发脉冲的产生方式主要有计算法和调制法。当前采用计算法控制方式的主要有预测电流控制，它是通过预测下一个时刻的参考电流和当前时刻的检测电流计算出开关管的占空比，这种控制方式具有控制精度高、易于数字化实现等优点，但缺点是对系统参数依赖性强。当前采用调制法控制方式的有比例积分控制、滞环跟踪控制和比例谐振控制[1-7]。其中，比例积分控制方法简单，技术成熟，应用广泛，但对正弦参考量的稳态误差难以消除[8]；滞环跟踪具有控制方法简单、跟踪性能好、鲁棒性强等优点，但存在的缺点是电流纹波大，且开关频率的不固定导致滤波电感的设计困难[9-13]。比例谐振控制是为解决比例积分控制稳态误差难以消除而产生的，它可实现无静差控制，但存在的缺点是参数的设计和数字化实现比较困难。

一个性能优越的并网逆变器调节策略应具备稳态误差小、开关频率固定、易于数字化实现等优点[14-16]。针对传统控制中存在的问题，本文提出一种应用于单相并网逆变器的电流频谱可控的模型预测控制方法。这种控制方法的触发脉冲产生方式既不属于计算法，也不属于调制法。它将所有的开关状态带入控制系统的离散数学模型，选取可使预测电流值和参考电流值最小的开关状态，将其作为逆变器下一个时刻的开关状态。这种控制方法物理模型清晰，并网电流频谱集中，易于实现数字化；与传统的单相并网逆变器控制方式相比，省去了PI参数整定环节，并且控制原理简单易懂。设置数字滤波器可实现并网电流频谱可控，不仅有利于减小器件开关损耗，同时容易设计交流侧滤波器。仿真与实验结果表明，模型预测控制具有很好的电流跟踪性能和抗扰动性能。

1 单相并网逆变器的离散数学模型

单相并网逆变器的电路原理如图1所示。

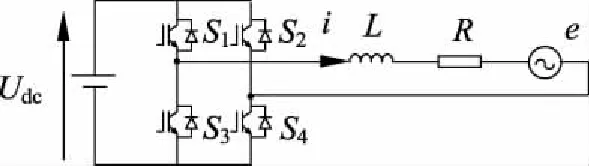
图1 单相并网逆变电路图Fig.1 Circuit of single grid connected-inverter

逆变器的开关状态函数Sa、Sb定义如下：

逆变器的开关状态矢量定义为

(3)

式中a=ejπ。

逆变器输出电压矢量u可表示为

u=UdcS

(4)

式中Udc为直流侧电压值。

考虑单相逆变器的所有开关状态，直流侧在交流侧形成4个电压矢量，如表1所示。

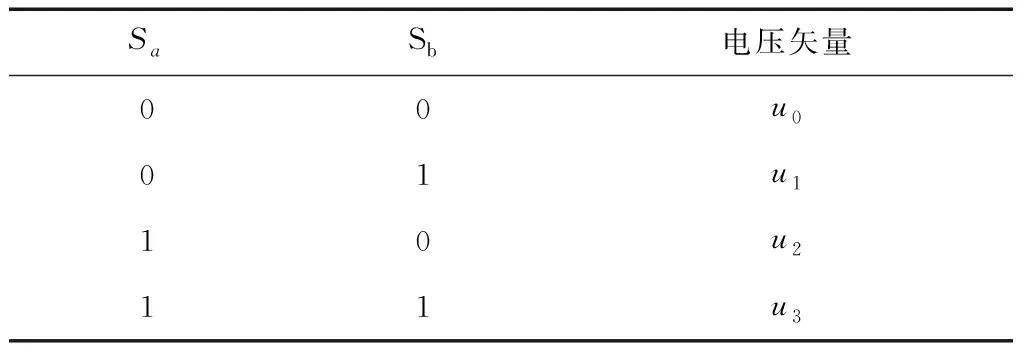
表1 单相逆变器形成的电压矢量Table 1 Voltage vector of a single phase inverter

根据图1，由基本电路原理得到如下系统模型：

(5)

式中：R为等效电阻；La为交流电抗实际电感量；u为逆变器交流输出电压；e为电网电压。

设系统实际采样时间为Tsa，则并网电流的微分可近似表示为

(6)

将式(6)代入式(5)可得i(k)表达式如下：

(7)

式中i(k-1)为上一时刻的并网电流值。

2 电流频谱可控的模型预测控制

2.1 电流频谱可控的模型预测控制方法

模型预测控制的结构如图2所示，控制策略有以下3个步骤：1)构建逆变器的交流输出电压矢量;2)构建并网电流的预测模型;3)定义一个指标函数G。

图2 模型预测控制结构图Fig.2 Structure of model predictive control

模型预测控制实现过程如下：

1) 首先由式(4)得到4个开关状态对应的电压矢量u0、u1、u2、u3，将所有电压矢量和系统检测量代入式(7)，根据系统模型对并网电流进行预测。

2) 然后设定如下指标函数G。

G=i*(k)-i(k)

(8)

3) 评估不同电压矢量作用下指标函数值的大小，选择指标函数G值最小时所对应的电压矢量，以实现并网电流的快速跟踪控制。

2.2 数字滤波器的设计

为改善控制器性能，本文通过对指标函数G添加数字滤波器作为约束条件，以实现并网电流频谱可控。

G=F(z)(i*(k)-i(k))

(9)

式中F为一个数字滤波器，定义为

(10)

利用数字滤波器调节并网电流频谱，实现开关频率近似恒定的控制效果，滤波器的设计直接影响系统性能。为了让并网电流的频谱集中在某些固定频谱上，数字滤波器应当选择一个窄带带阻滤波器。通过窄带带阻滤波器对目标函数进行处理，消去带阻滤波器中心频率及其整数倍附近的频谱影响，从而使并网电流的频谱集中在这个带阻滤波器中心频率及其整数倍附近。数字滤波器的设计方法很多，本文利用Matlab中的Filter Design & Analysis Tool工具箱进行数字滤波器参数设计。中心频率设为4 kHz，滤波器类型设为巴特沃斯带阻滤波器，阶数设置为10，采样频率设为100 kHz，上下限频率分别设置为3.8和4.3 kHz，截止频率处固定衰减3 dB。经运算该数字滤波器的分子系数B=[0.880，-7.089，27.229，-65.106，106.869，-125.561，106.869，-65.106，27.229，-7.089，0.880]，分母系数A=[1.000，-7.845，29.369，-68.445，109.515，-125.433，104.085，-61.826，25.214，-6.401，0.775]。该数字滤波器的幅频特性如图3所示。

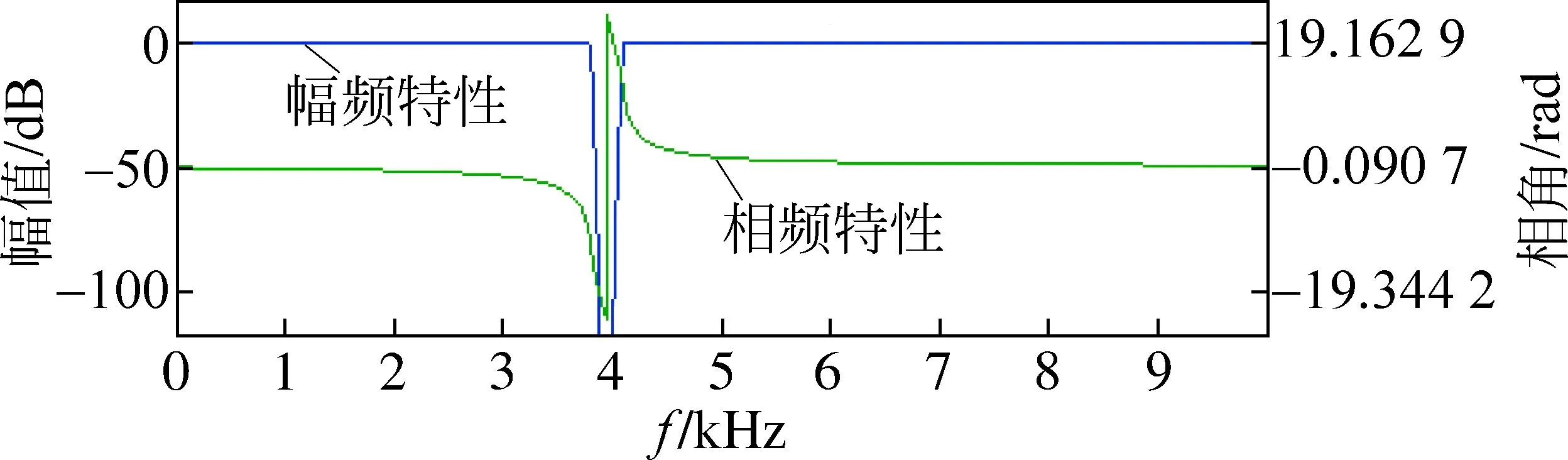
图3 中心频率为4 kHz的带阻滤波器幅频特性图Fig.3 Amplitude-frequency characteristic of band-stop filter with a 4 kHz center frequency

2.3 模型预测控制的稳定性和鲁棒性分析

在分析模型预测控制的稳定性和鲁棒性之前，首先要对模型预测控制进行数学建模。通过式(5)，忽略等效电阻R的影响，可得到离散后的电压方程为

(11)

式中：L为交流电抗理想电感量；Ts为理想采样时间。

离散后的参考电压方程为

(12)

式中u*(k)为并网逆变器输出电压参考值。

将式(11)、(12)相减可得u(k)的表达式如下：

(13)

式中ie(k)=i*(k)-i(k)。

根据拉格朗日的2阶外推公式[8]，u*(k)可表示为

u*(k)=3u(k-1)-3u(k-2)+u(k-3)

(14)

同理，ie(k)可表示为

ie(k)=3ie(k-1)-3ie(k-2)+ie(k-3)

(15)

将式(14)、(15)带入式(13)可得

(16)

根据式(16)、(7)可得模型预测控制传递函数，如图4所示。

图4 模型预测控制的传递函数框图Fig.4 Transfer function block diagram of model predictive control

忽略电网的扰动e(k)以及理想采样时间和实际采样时间的误差，由模型预测控制的传递函数框图可知，模型预测控制的传递函数为

(17)

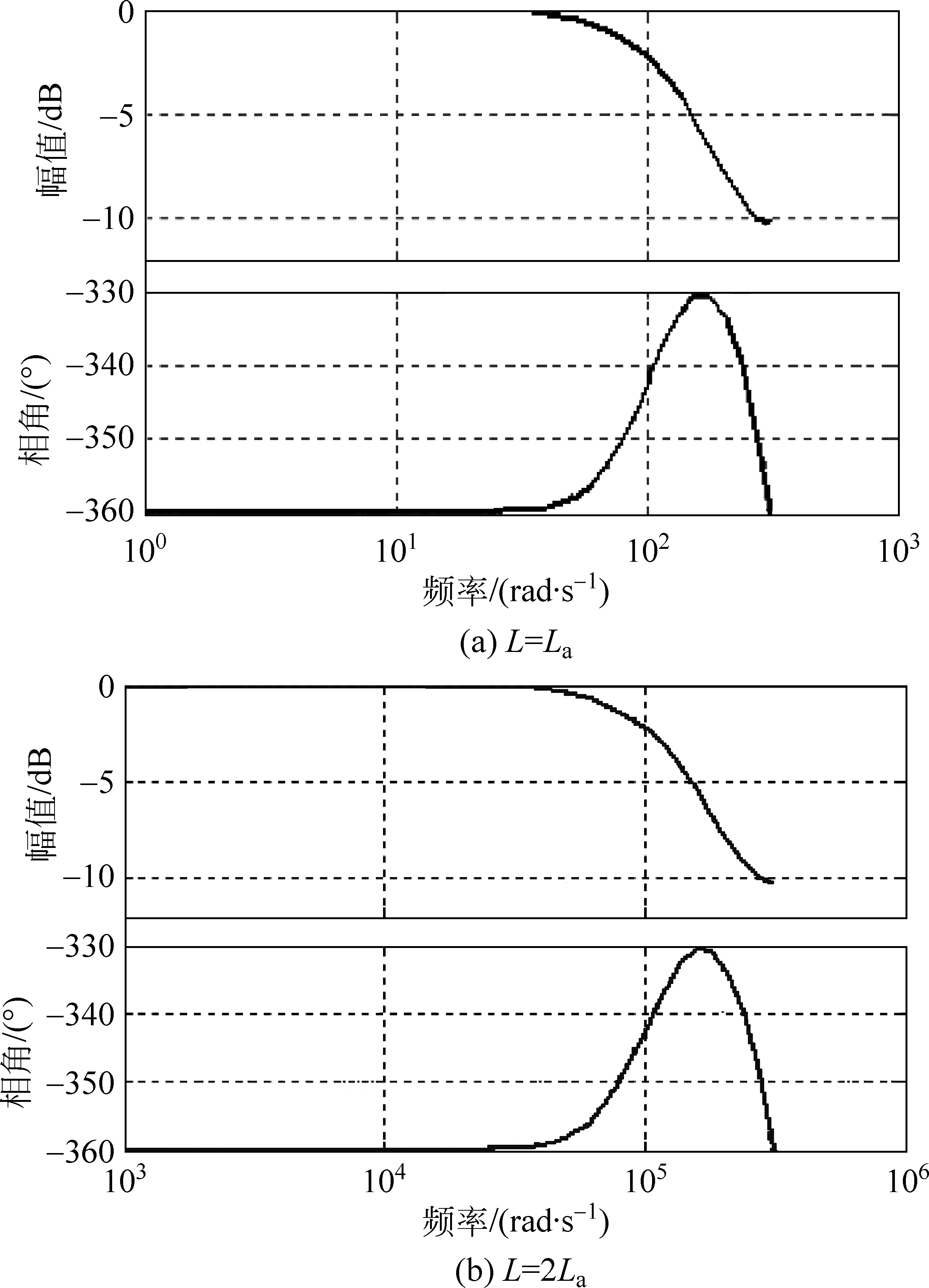
图5 模型预测控制的Bode图Fig.5 Bode diagram of model predictive control

L=La和L=2La时，控制系统的幅频特性曲线如图5所示。由图5可看出，模型预测控制具有足够的幅频裕度和相频裕度，说明模型预测控制具有很强的稳定性。当系统的主要参数电感发生变化时，模型预测控制仍有足够的幅频裕度和相频裕度，说明模型预测控制具有较强的鲁棒性。

为了验证加入数字滤波器后系统是否稳定，在误差电流后加入一个中心频率为4 kHz的带阻滤波器，其奈奎斯特曲线如图6所示。从图6中可看出，加入数字滤波器不影响模型预测控制系统的稳定性。

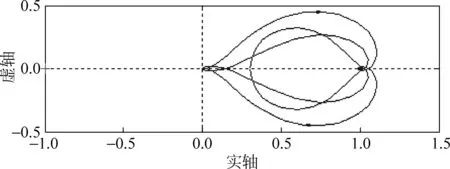
图6 加入数字滤波器后的控制系统奈奎斯特图Fig.6 Nyquist diagram of model predictive control with a digital filter

2.4 模型预测控制的程序流程图

根据模型预测控制的相关原理及算法其程序流程如图7所示。

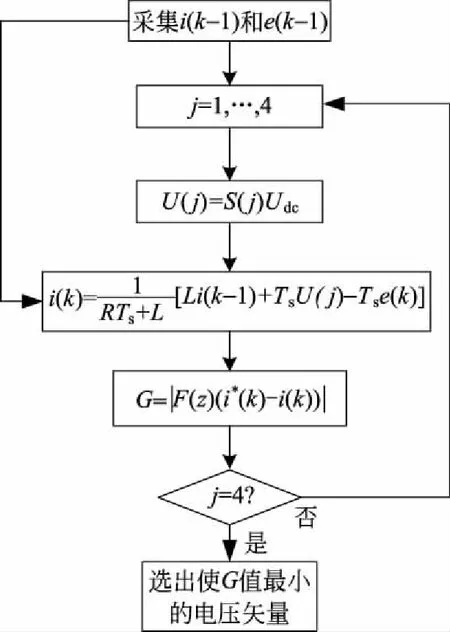
图7 模型预测控制的程序流程图Fig.7 Program flow chart of model predictive control

将所有的电压矢量和系统检测量带入并网电流的离散时间模型，并求得所有并网电流预测值。将这些并网电流的预测值和给定值代入指标函数，选出指标函数最小值对应的电压矢量，根据这个电压矢量对应的开关状态来控制逆变器下一时刻的输出。

3 仿真分析

为验证所提出的模型预测控制的效果，同时测试系统参数变化对控制器性能的影响以及数字滤波器改善并网电流频谱的效果，首先基于Matlab进行了单相并网逆变器的仿真分析。仿真模型中的参数如下：Udc=500 V，R=0.5 Ω，L=5 mH，e=220 V，Ts=100 μs。

图8为未加数字滤波器时的仿真波形，此时的谐波畸变率为4.8%。由图8(a)、(b)可看出，并网电流实现了完美跟踪且跟踪误差在10%以内；由图8(c)可见，并网电流的波形畸变率虽然很低，但频谱不集中，不利于器件开关损耗的估计和交流滤波器的设计。

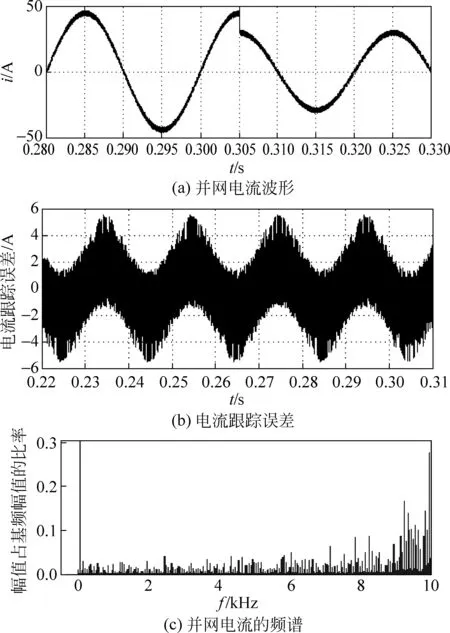
图8 未加数字滤波器时的仿真波形Fig.8 Simulation waveform of system without digital filter

为检验模型预测控制的鲁棒性，将上述仿真电路中的电阻R改为0.8 Ω，将电感L改为3 mH，其余参数不变，其仿真波形如图9所示。

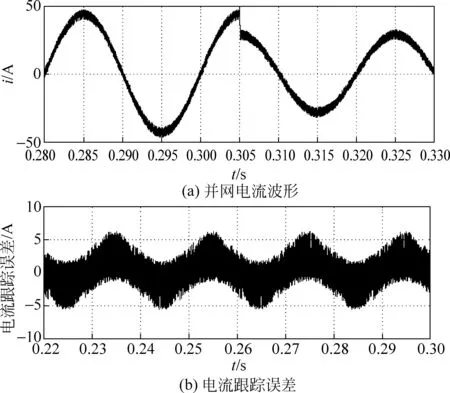
图9 参数变化后未加数字滤波器时的仿真波形Fig.9 Simulation waveform of system without digital filter after parameter changing

由图9可看出，参数改变后并网电流仍有良好的动态性能，且跟踪误差在10%左右。通过以上对比可发现，模型预测控制对参数的依赖度不强，表现出了较强的鲁棒性。

为改善模型预测控制的并网电流频谱，图10、11分别是加入中心频率为2和4 kHz的带阻滤波器的波形。

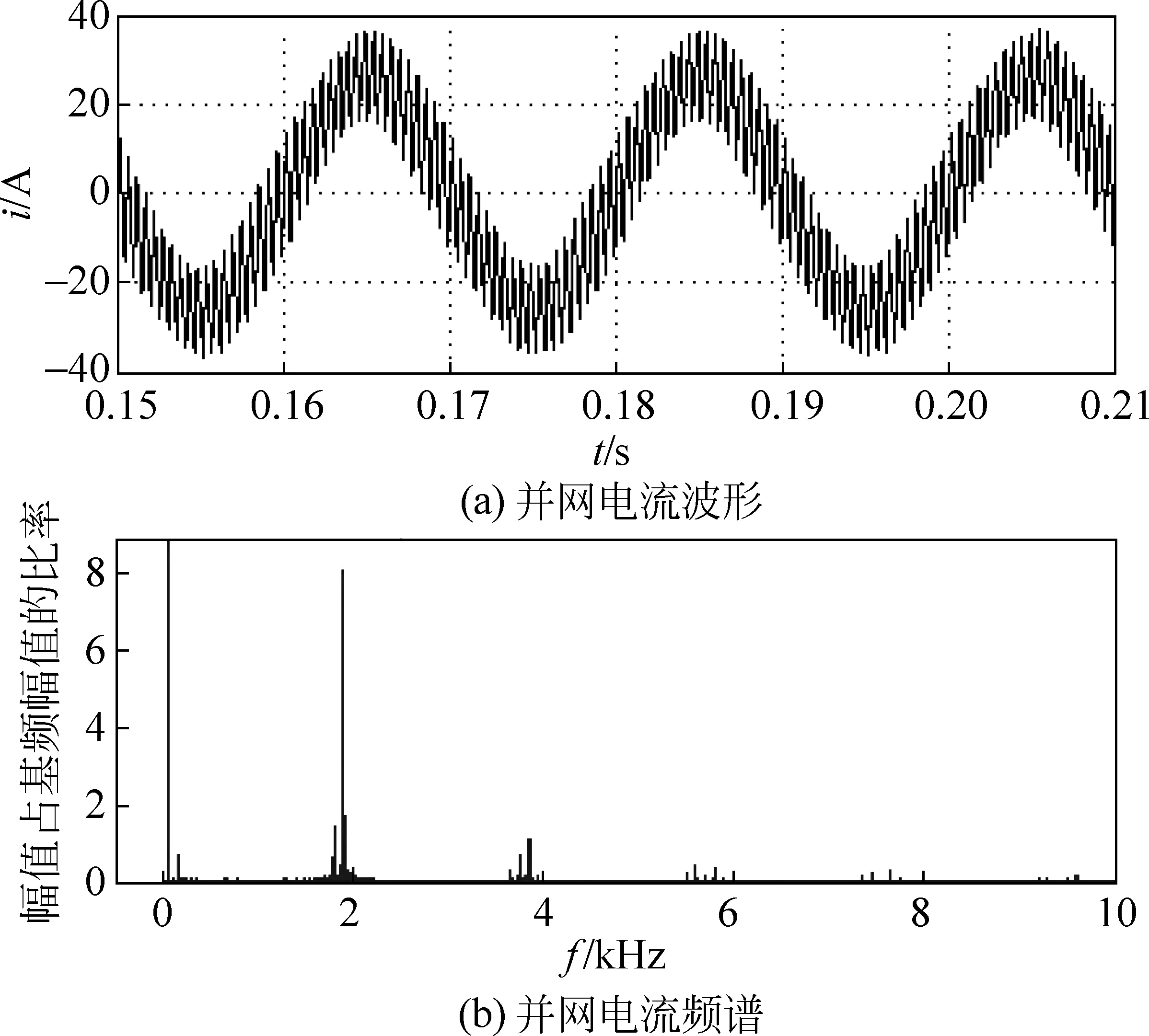
图10 加入中心频率为2 kHz数字滤波器后的仿真波形Fig.10 Simulation waveform of systemwith a center frequency of 2 kHz digital filter

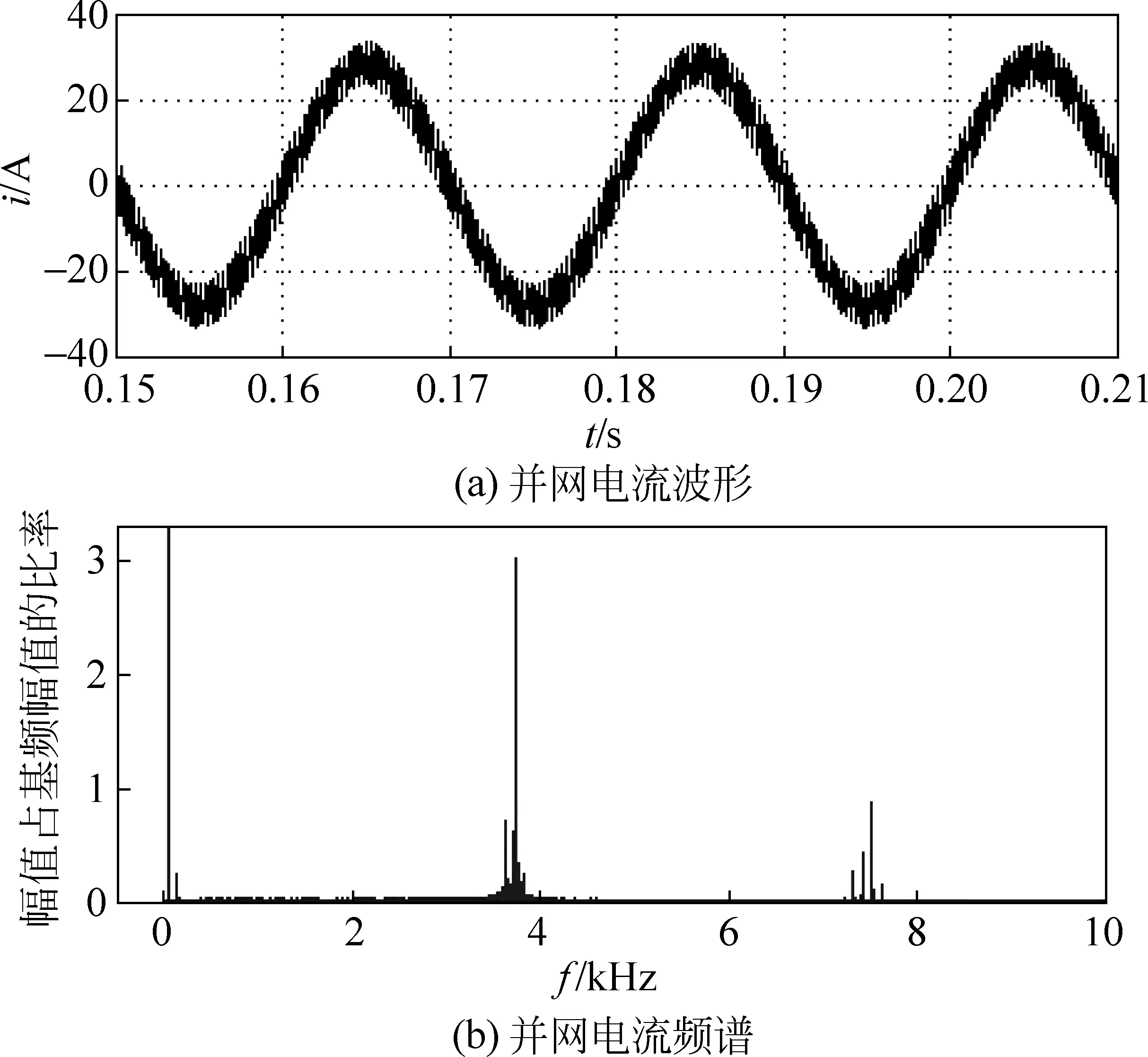
图11 加入中心频率为4 kHz数字滤波器后的仿真波形Fig.11 Simulation waveform of system with a center frequency of 4 kHz digital filter

由图10(a)可看出，并网电流可实现跟踪，但跟踪误差较大；由图10(b)可看出，并网的频谱主要集中在2 kHz及其整数倍附近。

由图11(a)可看出，并网电流可实现跟踪，但跟踪误差较小；由图11(b)可看出，并网的频谱主要集中在4 kHz及其整数倍附近。

通过对比分析，可得出以下结论：

1) 加入数字滤波器的模型预测控制在稳态情况下控制效果有所降低，但有效改善了并网电流的频谱；

2) 改变带阻滤波器的中心频率可控制并网电流的频谱。

4 结论

本文提出了一种应用于单相逆变器的频谱可控的模型预测控制方法。这种控制方法利用系统的预测模型实现对输出电流的快速跟踪，需在每个控制周期评估预测控制效果，选择可使电流跟踪误差最小的电压矢量，找出与该矢量对应的开关信号以完成逆变器的控制。为改善并网电流的频谱，在模型预测控制的指标函数中加入数字滤波器。这种控制方法物理模型清晰，并网电流频谱集中，易于实现数字化；与传统的单相并网逆变器控制方式相比，省去了PI参数整定环节，并且控制原理简单易懂。设置数字滤波器可实现并网电流频谱可控，不仅有利于减小器件的开关损耗，同时更易于设计交流侧滤波器。仿真和实验结果表明：控制器对并网电流的跟踪性能良好；同时，并网电流频谱分析显示出了类似开关频率恒定的控制效果。

[1] 于晶荣, 滕召胜. 有源电力滤波器预测电流控制及稳定性分析[J]. 电工技术学报, 2009, 24(7): 164-170.

YU Jingrong, TENG Zhaosheng. Predictive current control and stability analysis of active power filter[J]. Transactions of China Electrotechnical Society, 2009, 24(7): 164-170.

[2] RODRIGUEZ J, PONTT J, SILVA C A, et al. Predictive current control of a voltage source inverter[J]. IEEE Trans. on Industrial Electronics, 2007, 54(1), 495-503.

[3] 孙向东, 任碧莹, 钟彦儒, 等. 滤波电感在线估计方法在预测电流控制中的应用[J]. 电工技术学报, 2009, 24(7)： 150-156.

SUN Xiangdong, REN Biying, ZHONG Yanru, et al. An online estimation method of the filter inductance for a predictive current control[J]. Transactions of China Electrotechnical Society, 2009, 24(7) : 150-156.

[4] HOSSEIN M K, IDRIS A G, LIUCHEN C, et al. A novel DSP-based current-controlled PWM strategy for single phase grid connected inverters[J]. IEEE Transactions on Power Electronics, 2006, 21(4): 985-993.

[5] 章兢, 于晶荣. 基于 ADALINE 的有源电力滤波器预测电流控制策略[J]. 电工技术学报, 2009, 24(6): 77-84.

ZHANG Jing, YU Jingrong. Predictive current control strategy based on adaline for active power filter[J]. Transactions of China Electrotechnical Society, 2009, 24(6): 77-84.

[6] HOLTZ J. Pulse width modulation-asurvey[J]. IEEE Transactions on Industry Electronics, 1992, 39(5): 410-420.

[7] CORTES P, RODRIGUEZ J, QUEVEDO D E, et al. Predictive current control strategy with imposed load current spectrum[J]. IEEE Transactions on Power Electronics, 2008, 23(2): 612-618.

[8] 刘剑, 谭甜源, 乐健. 三角波比较法的幅值和相位补偿原理[J]. 电力系统自动化, 2010, 34(16): 69-72.

LIU Jian, TAN Tianyuan, YUE Jian. Amplitude and phase compensation of ramp comparison control[J]. Automation of Electric Power Systems, 2010, 34(16): 69-72.

[9] 陈东华, 纪志成. 适用于飞机电网的并联型有源电力滤波器功率电路及其控制策略[J]. 电网技术, 2008, 32(13): 75-79.

CHEN Donghua, JI Zhicheng. Power circuit of shunt active power filter suitable to aircraft power supply network and its control strategy[J]. Power System Technology, 2008, 32(13): 75-79.

[10] 洪峰, 单任仲, 王慧贞, 等. 一种变环宽准恒频电流滞环控制方法[J]. 电工技术学报, 2009, 24(1): 115-119.

HONG Feng, SHAN Renzhong, WANG Huizhen, et al. Varied hysteresis-band current controller with fixed switching frequency[J]. Transactions of China Electrotechnical Society, 2009, 24(1): 115-119.

[11] 谈龙成, 陈永刚, 常国洁, 等. 有源电力滤波器的电流控制新方法[J]. 电网技术, 2006, 30(21): 62-65.

TAN Longcheng, CHEN Yonggang, CHANG Guojie, et al. Anovel current control method for active power filter[J]. Power System Technology, 2006, 30(21): 62-65.

[12] 曾江, 刘艳, 叶小军, 等. 有源滤波器的低损耗滞环电流控制方法[J]. 电网技术, 2010, 34(1): 73-78.

ZENG Jiang, LIU Yan, YE Xiaojun, et al. A novel hysteresis current control method for active power filter with low switching loss[J]. Power System Technology, 2010, 34(1): 73-78.

[13] 郑建勇, 王杰, 梅军． 基于电压空间矢量的滞环电流控制方法和APF的系统设计[J]. 电力自动化设备, 2011, 31(5): 49-52.

ZHENG Jianyong, WANG Jie, MEI Jun, et al. Hysteresis current control based on voltage space vector and APF system design[J]. Electric Power Automation Equipent, 2011, 31(5): 49-52.

[14] 于蓉蓉, 魏学业, 吴小进, 等. 一种改进型预测电流控制算法[J]. 电工技术学报, 2010, 25(7): 100-107.

YU Rongrong, WEI Xueye, WU Xiaojin, et al. An improved predictive current control algorithm[J]. Transactions of China Electrotechnical Society, 2010, 25(7): 100-107.

[15] BODE G H, LOH P C, NEWMAN M J, et al. An improved robust predictive current regulation algorithm[J]. IEEE Transactions on Industry Applications, 2005, 41(6): 1720-1733.

[16] JEONG S J, KIM B W, SONG S H. Improvement of predictive current control performance using on-line parameter estimation in phase controlled rectifier[J]. IEEE Transactions on Power Electronics, 2007, 22(5): 1820-1825.