考虑不确定性因素的配电网分布式电源选址定容

王丽娜

(山东电力工程咨询院有限公司, 山东 济南 250013)

0 引言

随着新能源发电技术和经济性的提高，分布式电源(distribution generation, DG)在配电网中的渗透率持续提高[1]。DG为波动性电源，其出力随环境而变化，具有一定的随机性；系统中的负荷也往往具备一定的不确定性[2]。随着配电网中DG渗透率的增高，如果在DG的选址和定容中不能合理地考虑这些不确定性因素，有可能给配电网的经济运行、电压质量、甚至安全运行带来风险[3]。

目前，国内外对配电网中DG的优化配置研究很多，取得了一定的成果。这些研究多数未考虑DG及负荷的不确定性，往往采用确定性的规划方法[4-6]：在规划目标方面，多以DG成本、网络损耗等为目标，在考虑多目标时，往往又简单地将多目标优化问题转化为单目标优化问题[5,7-8]；在模型的求解上，主要采用传统的最优化算法和群智能启发式优化算法[4-8]。文献[5]在多优化目标中考虑了电压偏移；文献[8]在多优化目标中考虑了环境效益，丰富了优化模型。文献[7-8]计及了DG出力的不确定性，并分别利用蒙特卡洛模拟嵌入遗传算法和蒙特卡洛模拟嵌入改进粒子群算法求解优化模型；但这些基于蒙特卡洛嵌入启发式算法的模型计算规模较大，且直接将多目标简单加权，化为单目标优化问题。

本文在对DG的优化配置建模中，设置优化目标为网络总损耗最小、电压偏移量最小、系统稳定性最高；对DG和负荷的概率特性进行建模，并利用机会约束对其不确定性进行处理；采用广义回归神经网络(generalized regression neural networks, GRNN)与随机模拟结合的方法对配置方案的指标进行计算，并结合多目标粒子群算法求解其Pareto解集。仿真结果表明，本文所提方法能够快速、有效地得到合理的DG配置方案。

1 不确定性因素建模

1.1 DG输出功率的不确定性

本文考虑2种最为常见的DG——光伏发电(photovoltaic，PV)和风力发电(wind turbine generator，WT)，并以概率模型对其出力的不确定性进行描述。

PV的最大影响因素为太阳辐照强度，为简化模型，一般情况下可只考虑光伏出力Ps与太阳辐照强度s的关系[9]，即有

(1)

式中：Ps-r为光伏发电的额定出力;sr为额定太阳辐照强度，即光伏额定出力所需的最小太阳辐照强度。太阳辐照强度基本服从Weibull分布，其概率密度函数如下[9]：

(2)

式中：ks为形状指数;cs为规模指数。二者均可由当地的日照强度历史数据来确定。

WT的输出功率主要与风速相关，一般可认为风速v近似服从 Weibull分布，其概率密度函数与光照概率密度函数的形式相同，其分布曲线形状指数和规模指数可根据当地的风速历史数据确定。WT出力Pw与风速v的关系如下[10]：

(3)

式中：Pw-r为WT的额定功率;vci、vco和vr分别为切入风速、切出风速和额定风速(即额定风电机组出力所需的最小风速)。

1.2 负荷的不确定性

在配电网的某一运行方式下，其各区域内的负荷具有一定的不确定性，各节点的负荷符合一定的概率特性，负荷功率可近似认为符合正态分布[11]，其概率密度函数为

(4)

式中：PL为负荷功率;μp和σp2分别为负荷功率的期望值和方差。

2 多目标DG优化布置模型

本文以最为经典的两种DG作为研究对象，对PV和WT在配网中的接入位置和接入容量进行优化。目前，国内DG项目中上网电价高于当地脱硫燃煤机组的上网电价的部分，是通过向用户征收额外电价的方式解决的，因此，从配电公司的角度可不必考虑DG的固定投资及运行维护费用[12]。本文建立了计及系统经济性和稳定性的优化模型，目标函数为网络损耗最小、系统电压稳定性最高和电压偏移最小。

2.1 目标函数

2.1.1 配电网网络损耗

网络损耗是DG配置方案经济性的重要指标之一。DG接入配网后，一般情况下会减小支路潮流，进而减小网络损耗；但当DG配置不当时，可能会使支路潮流反向流动，使网络损耗增加。优化模型的第1个目标函数为网络损耗最小：

(5)

式中：N为网络支路总数；Gk(i,j)为节点i和j之间的线路k对应的电导；Ui、Uj和θi、θj分别为节点i和j的电压幅值和相位。

2.1.2 配电网电压稳定性

不合理的DG配置有可能影响到配电网电压水平的稳定，甚至影响到配电网的稳定性。通常采用电压稳定指标(voltage stability index，VSI)来表征电网的电压稳定性。根据文献[13]，对于支路k，VSI为

(6)

式中:Rij和Xij分别为支路k的电阻和电抗；Pj和Qj分别为支路k接收端点j的有功和无功功率。

VSI越小，电网的电压稳定性越高，全网的电压稳定指标为各支路VSI的最大值。本文模型的第2个目标函数为

minf2=VSI=max(VSI1,VSI2，…，VSIN)

(7)

2.1.3 配电网网络节点电压偏移

节点电压水平是配网电压质量的主要指标之一，也是评价配网电源规划合理性的主要指标之一。一般情况下，DG的接入能够改善系统功率因数，支撑节点电压，降低节点电压偏移。文献[14]给出了较为合理的节点电压偏移指标，计算首节点电压与其他节点电压偏差的均值，并考虑了节点重要等级。第3个目标函数为

(8)

式中：NN为节点总数；Ui和U0分别代表第i个节点和首节点的电压幅值；wi为第i个节点的权重因子，wi满足

(9)

2.2 DG优化布置模型的约束条件

2.2.1 机会约束

在系统正常运行中，可容许个别线路出现短时的过负荷现象。这是因为线路的极限值一般由其热容量决定，短时的过负载并不会使线路达到其热稳定极限。但过负荷情况应该较大程度地被限制，另外,考虑到电源功率和负荷的不确定性，该约束适合用软约束的形式表示[7]。本文采用如下的条件约束表示：

pr{Sij≤Sijmax}≥β

(10)

式中：Sij、Sijmax分别为线路传输容量及其最大值；pr{·}表示事件{·}成立的概率；β为线路传输容量不过限的置信水平。

2.2.2 等式约束

模型的等式约束即为配电网的潮流方程，如下：

(11)

式中：Pi、Qi分别为节点i的有功和无功功率；θij为节点i、j的相位差；Gij、Bij分别为节点i、j之间的互电导与互电纳。

2.2.3 不等式约束

模型的不等式约束包括节点电压约束、DG有功和无功出力限值约束、DG最大准入容量的约束。

(12)

式中NDG为DG总数。

3 求解策略

3.1 GRNN拟合配电网潮流

考虑到DG出力和有功负荷的不确定性，当给定某个配置方案时，需要对该方案进行随机潮流计算，以确定该方案的优劣[8];因此，需要多次进行潮流计算，为降低计算规模，本文采用GRNN对潮流计算中的控制变量和状态变量进行非线性拟合，以训练好的GRNN代替后续求解过程中的每一次潮流计算。

GRNN是一种性能优良的机器学习算法，能够根据样本数据拟合输入、输出间的映射关系[15]，GRNN由4层节点构成，其结构如图1所示。

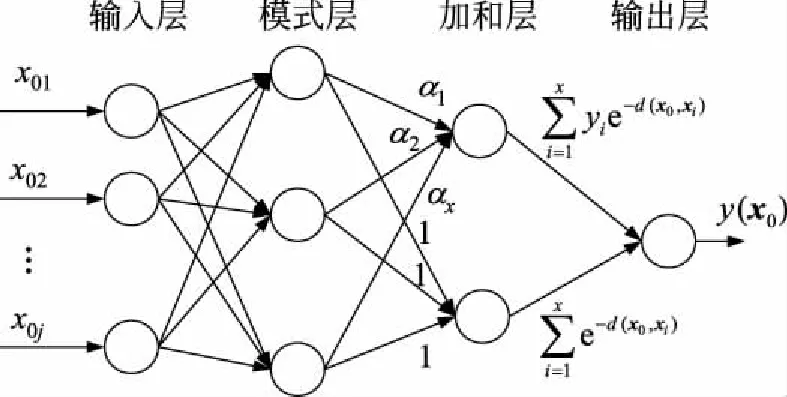
图1 GRNN结构节点配电系统Fig.1 GRNN structure of distribution network system

图1中：x0为输入向量，对应于潮流计算中的控制变量和状态变量，输入层节点个数等于输入向量维数，输入层与模式层的连接权值为1；模式层一般采用高斯核函数作为激活函数，xi为各单元核函数的中心矢量，d为高斯核函数的参数，与光滑因子对应；加和层有2个节点，分别为模式层的加权和和直接加和，αx为模式层节点与第1类加和层节点之间的连接权值；输出为第1类加和层节点的输出与第2类加和层节点的输出的商值。

本文采用随机抽样产生DG出力和负荷功率样本，然后代入潮流方程进行计算(采用前推回代法)，得到各节点的电压幅值和相角(状态变量)，以该样本对GRNN进行训练。当GRNN达到设定的训练精度后，即可用来模拟潮流计算。

3.2 机会约束条件的检验

本文基于蒙特卡洛模拟的思路对机会约束进行检验。基于随机变量的概率分布函数，对太阳辐照强度、风速、各节点的负荷功率进行Ns次独立抽样并计算对应的DG出力，然后代入GRNN中模拟随机潮流计算，并判断每一次潮流计算结果是否满足馈线容量约束。假设Ns次独立抽样中，有NF次满足馈线容量约束，最后判断NF/Ns是否大于馈线传输容量不越限的置信水平β：如果大于β，则可认为其满足机会约束条件；反之，则认为不满足。

3.3 多目标粒子群算法

本文采用文献[16]提出的基于拥挤距离的多目标粒子群算法求解多目标DG优化配置问题。以各优化配置方案作为粒子的位置，算法步骤如下：

1)初始化。给定种群规模M，最大迭代更新次数为Tmax，随机产生各个粒子的位置pi，置每个粒子的速度vi为0。计算每个粒子的初始适应度向量(即本文的3个目标函数)，筛选非劣解放入外部文档A，并将每个个体作为个体局部最优解。

2) 进行迭代寻优。每次从文档A的前10%随机挑选一个粒子作为当前全局最优位置G，按下式更新粒子的速度与位置：

(13)

式中：ω为惯性权重因子；c1、c2为学习因子；r1、r2为[0,1]之间的随机数；pib为粒子i的局部最优位置。更新过程中检查粒子位置是否越界，若越界则将其位置置于边界并将粒子的飞行方向置为反向，即-vi。

若迭代次数t≤MPm，Pm为变异率，对粒子位置pi执行高斯变异操作。计算每个粒子的适应度向量，将非劣解加入外部文档并剔除文档中的劣解。当外部文档达到最大容量时，计算非劣解的拥挤距离并排序，从拥挤度较大的10%中随机选择一个粒子，用新的非劣解将其替换。根据Pareto支配关系更新pi b，进行下一次迭代。

3) 优化结果。当达到最大迭代步数，外部文档中的粒子即为该问题的Pareto解集。

3.4 求解步骤

本文求解DG优化配置模型的步骤如下：

1) 随机抽样产生DG出力和负荷功率样本(假设各待选节点均接入DG)，进行潮流计算，以潮流结果训练GRNN。

2) 初始化粒子，即DG配置方案。

3) 采用蒙特卡洛方法和GRNN进行随机潮流计算，随机生成新的粒子来替换不满足约束条件的粒子，直至所有粒子满足约束条件。以随机潮流结果的期望值作为各优化目标。

4) 进行粒子更新。当更新后的粒子不满足机会约束时，采用步骤3)给出的替换方法；当更新后的粒子不满足不等式约束时，采用3.3节的更改方法。

5) 至迭代结束，输出Pareto最优解集，并进行潮流计算验证。

4 算例分析

4.1 模型设置

以图2所示的IEEE 37节点配电网[17]为例对本文所提模型进行测试。系统电压等级为35 kV，0号节点为系统平衡节点，系统基准容量为10 MW，系统总有功负荷的期望值为12 MW，总无功负荷的期望值为6 Mvar，假设各节点的有功和无功负荷的方差均为4.5，DG最大渗透率为35%。DG安装节点集合为{1,2,…,35}(节点36为变压器支路连接的末端节点，不考虑接入DG，且各节点最多安装一种DG)。线路容量的机会条件约束置信水平β设置为0.8，各节点电压偏移权重相同。假设光照强度分别服从ks=1.3、cs=1.5的Weibull分布，PV的功率因数为1.0；风速服从kw=2.2、cw=7.4的Weibull分布，vr=15 m/s，vci=4 m/s，vco=25 m/s，WT的功率因数为0.9。

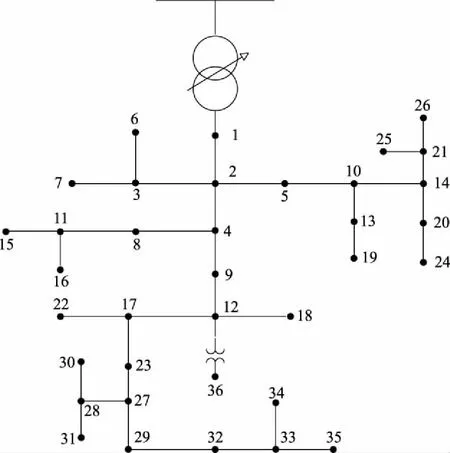
图2 IEEE 37节点配电系统Fig.2 IEEE 37-node distribution network system

GRNN训练样本的数量为100。多目标粒子群参数设置：种群规模M=100，最大迭代次数Tmax=250，惯性权重因子ω=0.4，学习因子c1=c2=0.5，变异率Pm=0.5，外部文档A的容量为50。

4.2 优化结果及分析

图3为采用本文模型得到的DG配置Pareto解的目标函数分布，即Pareto最优前沿。解1—3是有代表性的几个最优配置方案：解1为网络损耗最小对应的方案，解2为电压稳定性能最优和电压偏移最小对应的方案，解3为各指标均适中的一个典型方案。

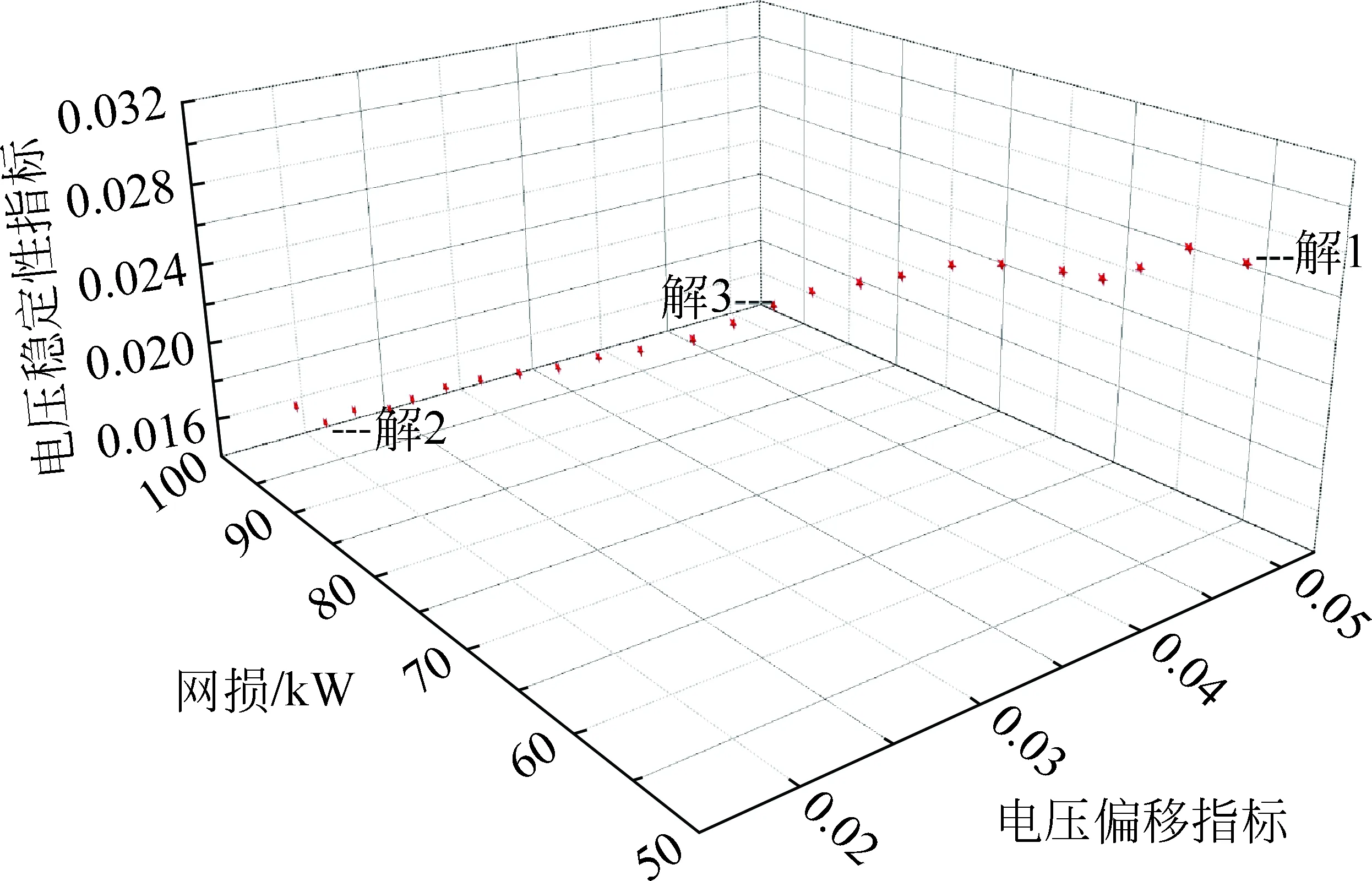
图3 DG配置的Pareto最优前沿Fig.3 Pareto optimal front of DG deployment

表1为各方案及其对比，由表1可看出：大部分的DG电源位于网络的末端，这是由于DG接入配网后，改变了潮流分布，使沿馈线传输的有功和无功功率减小，从而提升各节点的电压水平并降低网损。相比于未接入DG时，以上3种方案均较大程度地降低了网损，提升了电压水平和系统的电压稳定性：方案1较DG接入前，网损降低了75.32%；方案2较DG接入前，电压稳定指标提升了53.49%，电压偏移指标提升了80.28%。

为验证采用GRNN进行拟合潮流计算的精确度和时效性，将本文计算方法与直接采用前推回代法进行每一次潮流运算的方法进行对比，Pareto最优前沿基本一致，网络损耗最小时和电压稳定性指标、电压偏移指标最优时的方案相同。在Windows10系统，4 GB RAM，I3-3.1 GHz CPU，Matlab 7平台上进行仿真时，直接采用前推回代法进行潮流运算的模型耗时4 978.21 s，采用GRNN拟合潮流计算的模型耗时604.12 s。结果表明，本文方法能够得到合理的配置方案，并且大幅降低了计算规模。

5 结论

本文提出了一种配电网DG优化选址定容的模型：采用机会约束规划计及DG出力和负荷功率的不确定性；采用GRNN拟合配电网潮流运算；采用多目标粒子群算法求解优化方案。算例仿真证明本文方法能够得到合理的DG配置方案，主要结论如下：

表1 各DG配置方案对比Table 1 Comparison of DG configuration schemes

1) 采用多目标规划可兼顾各个规划目标，通过多目标优化方法得到Pareto解集，有助于规划者从不同的需求出发进行决策；

2) 采用GRNN对配电网潮流运算进行拟合，在保证求解有效性的同时，可大幅降低计算规模和计算耗时；

3) DG一般优先配置于配电网的末端，DG的接入可降低配电网的网络损耗，并提升配电系统的电压水平和电压稳定性。

[1] GEORGILAKIS P S, HATZIARGYRIOU N D. Optimal distributed generation placement in power distribution networks: models, methods, and future research[J]. IEEE Transactions on Power Systems, 2013, 28(3): 3420-3428.

[2] 杨佳俊, 雷宇, 龙淼, 等. 考虑风电和负荷不确定性的机组组合研究[J]. 电力系统保护与控制, 2014, 10(3): 63-70.

YANG Jiajun, LEI Yu, LONG Miao, et al. Study of unit commitment considering the uncertainty of wind farm and load[J]. Power System Protection and Control, 2014, 10(3): 63-70.

[3] EVANGELOPOULOS V A, GEORGILAKIS P S. Optimal distributed generation placement under uncertainties based on point estimate method embedded genetic algorithm[J]. IET Generation, Transmission & Distribution, 2013, 8(3): 389-400.

[4] EL-KHATTAM W, HEGAZY Y G, SALAMA M M A. An integrated distributed generation optimization model for distribution system planning[J]. IEEE Transactions on Power Systems, 2005, 20(2): 1158-1165.

[5] EL-ELA A A A, ALLAM S M, SHATLA M M. Maximal optimal benefits of distributed generation using genetic algorithms[J]. Electric Power Systems Research, 2010, 80(7): 869-877.

[6] ABU-MOUTI F S, EL-HAWARY M E. A priority-ordered constrained search technique for optimal distributed generation allocation in radial distribution feeder systems[C]//23rd Canadian Conference on Electrical and Computer Engineering (CCECE). Alberta: IEEE, 2010: 1-7.

[7] 刘志鹏, 文福拴, 薛禹胜, 等. 计及可入网电动汽车的分布式电源最优选址和定容[J]. 电力系统自动化, 2011, 35(18): 11-16.

LIU Zhipeng， WEN Fushuan， XUE Yusheng， et al． Optimal siting and sizing of distributed generators considering plug-in electric vehicles[J]. Automation of Electric Power Systems， 2011， 35(18)： 11-16．

[8] 彭显刚, 林利祥, 刘艺, 等. 计及电动汽车和可再生能源不确定因素的多目标分布式电源优化配置[J]. 电网技术, 2015, 39(8): 2188-2194.

PENG Xiangang, LIN Lixiang, LIU Yi, et al． Multi-objective optimal allocation of distributed generation considering uncertainties of plug-in electric vehicles and renewable energy sources[J]. Power System Technology, 2015, 39(8): 2188-2194.

[9] MUTOH N, MATUO T, OKADA K, et al. Prediction-data-based maxim um-power-point-tracking method for photovoltaic power generation systems[C]//Power Electronics Specialists Conference, Queensland, Australia, 2002: 1489-1494.

[10] ATWA Y M, EL-SAADANY E F, SEETHAPATHY R, et al. Effect of wind-based DG seasonality and uncertainty on distribution system losses[C]//NAPS’ 08. Alberta， Canada: IEEE, 2008: 1-6.

[11] 刘健, 徐精求, 董海鹏. 配电网概率负荷分析及其应用[J]. 电网技术, 2004, 28(6): 67-70.

LIU Jian, XU Jingqiu, DONG Haipeng． Probabilistic load flow analysis of distribution network and its application[J]. Power System Technology, 2004, 28(6): 67-70.

[12] 李亮, 唐巍, 白牧可, 等. 考虑时序特性的多目标分布式电源选址定容规划[J]. 电力系统自动化, 2013, 37(3): 58-63.

LI Liang, TANG Wei, BAI Muke, et al. Multi-objective locating and sizing of distribution generators based on time-sequence characteristics[J]. Automation of Electric Power Systems, 2013, 37(3): 58-63.

[13] RANJAN R, DAS D. Voltage stability analysis of radial distribution networks[J]. Electric Power Components & Systems, 2001, 23(2): 129-135.

[14] 夏澍, 周明, 李庚银. 分布式电源选址定容的多目标优化算法[J]. 电网技术, 2011, 35(9): 115-121.

XIA Shu， ZHOU Ming， LI Gengyin. Multi-objective optimization algorithm for distributed generation locating and sizing[J]. Power System Technology, 2011, 35(9): 115-121.

[15] 孔雪卉, 张慧芬. 基于优化广义回归神经网络的变电站设备温度预测[J]. 中国电力, 2016, 18(7): 54-59.

KONG Xuehui, ZHANG Huifen. Temperature forecast for subs-tation equipment based on optimized general regression neural network[J]. Electric Power, 2016, 18(7): 54-59.

[16] RAQUEL C R, NAVAL J P C. An effective use of crowding distance in multi-objective particle swarm optimization[C]//Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation. New York, USA: ACM, 2005: 257-264.

[17] IEEE Distribution System Analysis Subcommittee. IEEE radial test feeders[EB/OL]. (2013-08-05)[2017-05-05]. http://www.ewh.ieee.org/soc/pes/dsacom/testfeeders/index.html.