基于NURBS曲线的螺杆转子型线反向设计研究

黄海楠HUANG Hai-nan 何雪明 - 张 荣 姜振钢 -

(1. 江南大学江苏省食品先进制造装备技术重点实验室，江苏 无锡 214122；2. 江南大学理学院，江苏 无锡 214122)

双螺杆压缩机因为性能优良、运行平稳、噪声低、体积小、维护方便等，被广泛应用于制冷[1-2]、食品[3-4]、石油、化工等行业，其核心零件为内部的一对阴阳转子。转子型线作为螺杆转子形状的重要特征，很大程度上决定了压缩机的工作性能及转子的加工制造性能。

目前转子型线的设计方法使用比较广泛的是正向设计：首先设计出阴转子(或者阳转子)的型线，再通过解析包络法推导出另一个转子的型线。Stosic等[5]根据齿条的啮合原理提出了由齿廓线到转子型线的设计方法，并开发了N型线；Su等[6]设立转子接触线长度、泄露三角形面积等性能参数作为目标，实现对转子型线的优化；Wu等[7]提出了基于标准齿条生成系统的螺杆转子轮廓设计方法，并通过对比论证阐释了该方法的优越性；何雪明等[8]提出了以自由曲线作为组成曲线的转子设计方法，丰富了转子型线线型的种类。

正向设计虽然比较成熟，但要判断所设计的转子型线及压缩机性能的优劣，必须在得到阴阳转子型线后，继续推导得到啮合线再做出判断，设计过程十分繁琐。针对正向设计的多个弊端，Zaytsev等[9-10]提出了反向设计转子型线的“啮合线法”，该方法是从啮合线出发推导出转子轮廓线，并通过实例验证了该方法的可行性；卜啸华等[11]推导了当啮合线曲线类型为圆弧、内摆线和外摆线时的螺杆转子型线计算公式；何雪明等[12]分别采用直线、圆弧、三次B样条曲线为啮合线段进行阴阳转子的反向设计。由此，啮合线推导转子型线的反向设计方法逐渐发展起来。

在反向设计的线型选择方面，现在已经发展到比较高级的B样条曲线，但B样条曲线的根基是多项式参数曲线，并不能表达基本的二次曲线，如圆弧、椭圆弧等。而NURBS曲线拥有更高的自由度和局部修改性，可以精确地表达圆弧、椭圆弧等二次曲线。本研究拟将NURBS曲线运用到反向设计中，旨在实现设计曲线线型的统一，并利用灵活的曲线修改手段进行转子型线优化设计。

1 啮合线法设计原理

已知双螺杆转子的啮合线的方程式是x0、y0关于参数t的方程，通过啮合线法求解转子轮廓线，需要建立如图1所示的坐标系，包括阳转子静坐标系O1X1Y1和阴转子静坐标系O2X2Y2、随转子转动的阳转子动坐标系O1x1y1和阴转子动坐标系O2x2y2，以及一个固结于机壳上的啮合线坐标系O0x0y0。其中阳转子逆时针转动，阴转子顺时针转动。图1中Ra1是阳转子齿顶圆半径，Rf2是阴转子齿根圆半径，满足Ra1+Rf2=H。以下下标为1都是指代阳转子坐标系中的参数，下标为2的指代阴转子坐标系中的参数。

图1 转子法中的坐标关系Figure 1 Relationships of coordinates in the rotor method

根据转子间的啮合传动原理可得：

(1)

φ1+φ2=(1+i)φ1=kφ1，

(2)

R1+R2=H，

(3)

式中：

φ2、φ1——阴、阳转子旋转角度，(°)；

n2、n1——阴、阳转子的转速，r/min；

ω2、ω1——阴、阳转子转动角速度，rad/s；

R2、R1——阴、阳转子节圆半径，mm；

z2、z1——阴、阳转子齿数；

i——阴转子和阳转子的传动比；

H——阴、阳转子中心距，mm。

根据上述的等式以及坐标转动中的几何关系，可以推导出下列几项坐标系之间的变换关系：

(1) 阳转子动坐标系O1x1y1与啮合线坐标系O0x0y0关系：

(4)

(2) 阴转子动坐标系O2x2y2与阳转子动坐标系O1x1y1之间的变换关系：

(5)

根据包络条件可以得到φ1关于参数t的等式[13]：

(6)

2 啮合线法的NURBS曲线包络条件

2.1 包络条件的求解

一段k次NURBS曲线的函数定义为[14]：

(7)

式中：

k——曲线次数；

Pi——控制点；

wi——控制点Pi的权因子，决定了控制点偏离曲线的程度，所有wi>0；

Ni,k(u)——定义在非周期且非均匀节点矢量U={a,…,a,uk+1,…,um-p-1,b,…,b}上的k次B样条基函数。

一段啮合线的NURBS曲线段的参数方程为：

0≤u≤1。

(8)

将式(8)代入式(6)中可以得到：

(9)

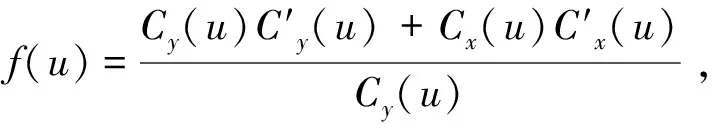
(10)

φ0是啮合的起始角度，对于啮合线的第一段曲线，取φ0=0。

f(u)=

(11)

由于被积函数f(u)的原函数无法用初等函数表达，因此需要采用数值积分法，本设计方法采用的是龙贝格(Romberg)求积公式[15-16]，也称为逐次分半加速法。龙贝格求积公式用的是一种外推算法，相比于其他计算方式，其计算量相对较小、精度较高，且易于编程计算。龙贝格求积公式为：

(12)

其中两个初始值的计算公式为：

(13)

(14)

由此得到φ1值后，再将值代入式(4)、(5)就得到了阴转子和阳转子对应的齿曲线段。

2.2 NURBS曲线的求导

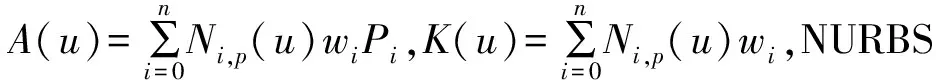
(15)

(16)

而A(u)与K(u)的导数都可以转换成关于基函数的导数，由式(17)～(20)求得：

(17)

(18)

(19)

(20)

式(17)～(20)中的基函数的一阶导数和二阶导数可以由式(21)求得。

(21)

(22)

可以看到式(21)～(22)是类似于求解基函数的一个递推公式，可以从低到高一阶一阶地计算出基函数导数的值。由此便可计算出NURBS曲线的一阶导数和二阶导数。

3 NURBS曲线啮合线的设计与优化

本研究针对用NURBS曲线对复盛型线[17]的啮合线进行反向设计，并通过误差分析，验证基于NURBS曲线的反向设计方法的可行性，并在此基础上，利用NUBRS的局部可调性对啮合线进行了优化设计。

3.1 NURBS曲线啮合线设计流程

NURBS曲线设计啮合线设计流程如图2所示，首先必须确定阴阳转子的中心距，然后利用NURBS直接设计出啮合线，根据NURBS曲线的数据推导出阴、阳转子型线数据，如果符合设计要求，则输出型线数据，不符合则需要修改设计参数，重新计算。

图2 NURBS曲线反向设计流程Figure 2 Reverse design process with NURBS curve

3.2 复盛型线的反向设计

复盛型线转子型线由圆弧、椭圆弧及其对应的包络线设计而成，见图3。圆弧以参数方程的形式表达为：

(23)

式中：

r——圆弧的半径，mm；

c1、c2——圆心横坐标和纵坐标，mm。

椭圆弧以参数方程的形式表达为：

(24)

式中：

a、b——椭圆的长短轴长，mm；

c1、c2——椭圆中心横坐标和纵坐标，mm。

复盛型线的各段齿曲线的详细设计参数见表1。其啮合线由阴阳转子齿曲线通过啮合条件式计算所得，表2给出了啮合线曲线段和转子齿曲线段的对应关系，生成的啮合线见图4。

根据复盛的啮合线数据，利用高精度的NURBS曲线来代替原有的啮合线[见图5(a)～(d)]进而得到了该啮合线每一段的控制点与权因子；然后将每一段啮合线的端点作为NURBS曲线的节点，利用累积弦长法计算出整段型线的节点矢量，使其成为一段式的啮合线[见图5(e)]，最终设计的这段啮合线只由控制点、权因子和节点矢量决定。进一步利用上文推出的NURBS曲线包络条件，得到了对应的阴阳转子型线，生成的型线误差数据见表3。

图3 复盛型线转子型线Figure 3 Rotor lines of Fusheng Profile

分析表3中数据可以发现：啮合线的最大精度误差出现在A0B0段，为0.092 μm；阳转子的最大精度误差在D1E1段，为0.442 μm；阴转子的最大精度误差出现在D2E2段，为0.443 μm。可以看出虽然各部分都存在精度误差，但都控制在0.5 μm以下，是能接受的范围。所以该实例验证了结合NURBS曲线和啮合线法设计转子型线方法的可行性。

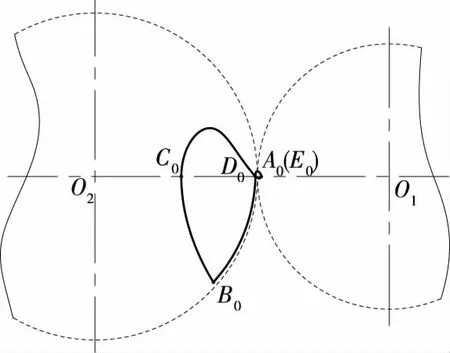
图4 复盛型线啮合线Figure 4 Meshing lines of Fusheng Profile

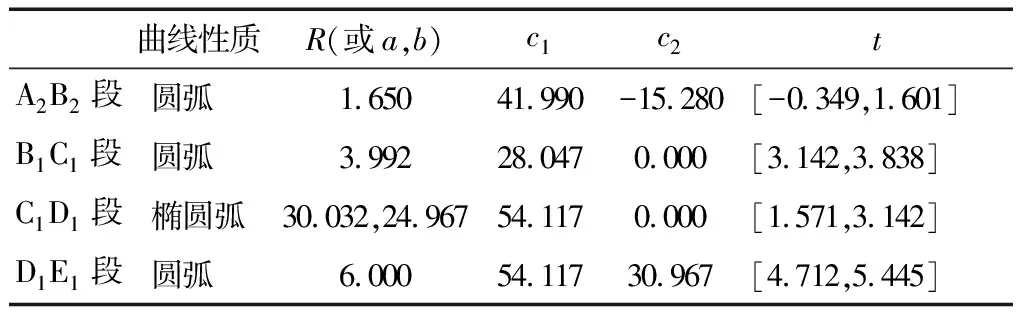
表1 复盛型线各段参数取值Table 1 Value of the parameters of the Fusheng Profile

表2 复盛型线设计相关数据Table 2 Design relevant data of Fusheng Profile

图5 获取复盛啮合线的NURBS曲线参数过程

Figure 5 Process of obtaining the NURBS curve parameters of the complex meshing line is obtained

表3 NURBS曲线啮合线误差数据Table 3 Error data of NURBS curve meshing line

3.3 啮合线的优化

根据NURBS曲线的局部修改性，通过移动控制点可以调整啮合线形状，对啮合线进行优化。对啮合线中b、c、d 3点进行了微调，阴阳转子的齿曲线发生相应的变化，见图6；转子型线性能参数发生相应的变化，其规律总结见表4[13]。所以可以根据这些变化规律对啮合线的线段进行修改，以达到优化型线性能的目的。

在不改变原有转子结构的情况下，如阴阳转子的齿顶圆弧大小、齿数比等参数，主要以减小泄漏三角形的面积和增大面积利用系数为目标对型线进行优化。即不移动图6中的c点位置，变化b和d 2点的位置。根据表4的规律，将啮合线的控制点a5、a6和b1～b4向外移动，使得啮合线交点下移，但不能超过阴阳转子齿顶圆的范围；然后移动控制点c2～c5，使得啮合线最高点下移，控制点移动对比见图7。优化啮合线后，阴阳转子齿曲线也发生了相应的变化，优化前后的对比见图8。阵列优化后的阴阳转子齿曲线得到完整的转子型线，见图9。

图6 啮合线顶点与阴阳转子型线变化关系

Figure 6 Relationship between the vertices of the meshing line and the yin-yang rotor line

表4型线性能参数与各顶点移动方向关系†

Table 4 Relationship between the linear performance parameters and the direction of each vertex movement

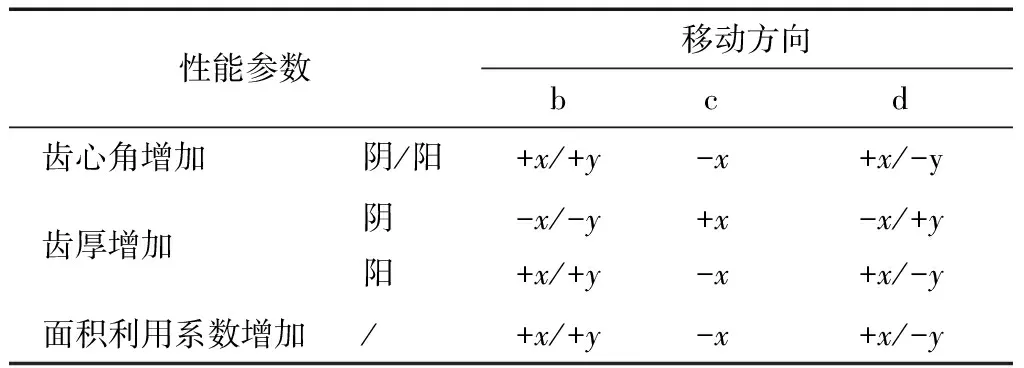
性能参数移动方向bcd齿心角增加 阴/阳+x/+y-x+x/-y齿厚增加 阴阳-x/-y+x/+y+x-x-x/+y+x/-y面积利用系数增加/+x/+y-x+x/-y

† “阴”表示阴转子，“阳”表示阳转子，“+x”表示向x轴正方向移动，“-x”表示向x轴负方向移动，“+y”、“-y”拥有类似的含义。

将优化前后的转子性能参数进行整理得到表5。由表5可知，优化后的型线增加了阴转子的厚度，阴转子的齿间面积减少了16.212 mm2，但阳转子齿间面积增加了32.678 mm2，所以面积利用系数提高了1%，而泄漏三角形的面积减少了5%。综上，优化后的转子性能得到了提升。

4 结论

(1) 利用龙贝格求积公式来解决啮合线法中原函数不能用初等函数表达的问题，实现了NURBS曲线的反向型线设计。

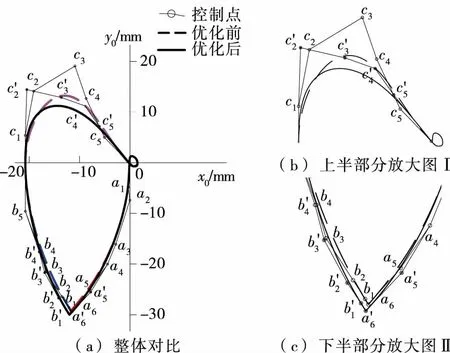
图7 型线改进优化前后控制点对比

Figure 7 Comparison of control points before and after optimization of meshing lines

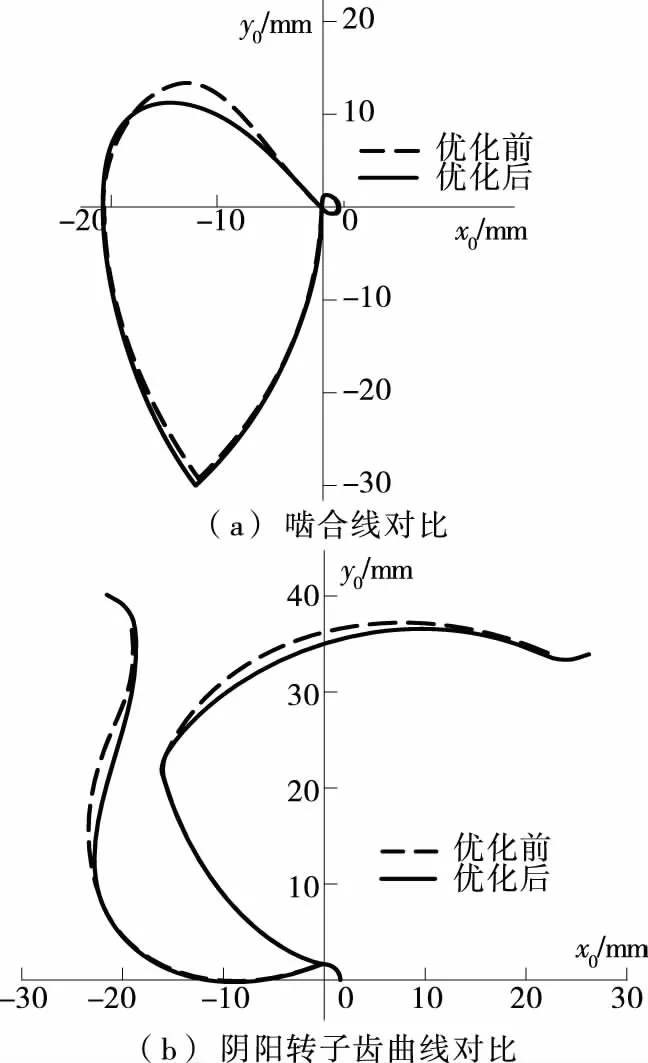
图8 型线优化前后对比Figure 8 Comparison of line optimization before and after optimization

图9 优化后的阴阳转子型线Figure 9 Yin-yang rotor profile after optimization

表5 优化前后性能参数对比Table 5 Comparison of performance parameters before and after optimization

(2) 针对典型型线复盛型线的啮合线进行反向设计，啮合线用一整段NURBS曲线表达，只由控制点、权因子和节点矢量决定，得到了误差在0.5 μm以内的型线，验证了用NURBS进行型线设计的可行性。增添了双螺杆压缩机转子型线设计的曲线类型。

(3) 根据啮合线顶点与型线性能的变化关系，利用NURBS曲线的局部修改性对型线进行优化。最终得到优化后的型线，增加了阴转子齿厚，增大了面积利用系数，减小了泄漏三角形的面积，整体性能得到了提升。

(4) 结合NURBS曲线和“啮合线法”反向设计转子型线，优势在于NURBS曲线的便捷的局部调整性，目前该方法只通过调整控制点的方式调控曲线，为了最大化利用NURBS曲线的形状调整工具，今后应将调整权因子的手段添加进来。

(5) 螺杆压缩机转子对加工精度要求非常高，所以在制造过程中应选择高精度的铣削或磨削加工方式，在加工过程中应特别关注可避免的加工误差的产生，如刀具的安装、磨损等产生的加工误差。

[1] 郭耀君, 谢晶, 朱世新, 等. 超低温制冷装置的研究现状和进展[J]. 食品与机械, 2015, 31(1): 238-243.

[2] STOSIC N, SMITH I K, KOVACEVIC A. A twin screw combined compressor and expander for CO2refrigeration systems[C] // STOSIC N. International Compressor Engineering Conference, Proceedings of the 2002. Purdue: Purdue University, 2002: 1 591-1 594.

[3] 傅廷振, 林雨晨. 无油空压机技术为食品行业带来纯净气源[J]. 食品安全导刊, 2016(7): 72-73.

[4] 阿特拉斯-科普柯公司. 阿特拉斯.科普柯公司在中国推出全新系列高效能压缩机[J]. 包装与食品机械, 2012, 30(6): 70.

[5] STOSICN, SMITH I K, KOVACEVIC A. Screw compressors: Mathematical modeling and performance calculation[M]. Berlin: Springer, 2005: 32-34.

[6] SU Shyh-haur, TSENG Ching-huan. Synthesis and optimization for rotor profiles in twin rotor screw compressors[J]. Journal of Mechanical Design, 2000, 122(4): 543-552.

[7] WU Yu-ren, FONG Zhang-hua. Rotor profile design for the twin-screw compressor based on the normal-rack generation method[J]. Journal of Mechanical Design, 2008, 130(4): 42 601-42 608.

[8] 何雪明, 戴进, 刘洪园. 基于自由曲线的螺杆转子型线的正反向设计[J]. 中国机械工程, 2012, 23(22): 2 752-2 757.

[9] ZAYTSEV D, FERRIRA C A I. Profile generation method for twin screw compressor rotors based on the meshing line[J]. International Journal of Refrigeration, 2005(28): 744-755.

[10] ZAYTSEV D, FERRIRA C A I. Screw compressor rotor profile generation method based on pre-defined meshing line[C]// 3rd International Compressor Technique Conference(ICTC 2001). Wuxi: [s.n.], 2001: 117-127.

[11] 卜啸华, 邹友金, 孟尔镛. 螺杆压缩机型线设计的逆命题法[J]. 上海理工大学学报, 1986(3): 43-51.

[12] 何雪明, 童洁, 戴进, 等. 双螺杆转子型线的反向优化设计及应用[J]. 机械设计与研究, 2015, 31(4): 151-157.

[13] 何雪明, 姜振钢, 武美萍, 等. 双螺杆压缩机转子啮合线与型线关系研究[J]. 中国机械工程, 2017, 28(7): 763-770.

[14] PIEGL L A, TILLER W. 非均匀有理B样条[M]. 2版. 赵罡, 穆国旺, 王拉柱, 等, 译. 北京: 清华大学出版社, 2010: 86-93.

[15] 邢诚, 王建强, 贾志强, 等. 多种数值积分方法比较分析[J]. 城市勘测, 2010(1): 104-106.

[16] 刘玉娟, 陈应祖, 卢克功. 龙贝格积分法及其应用编程[J]. 重庆科技学院学报: 自然科学版, 2007, 9(1): 97-99.

[17] LEE H T. Screw-rotor machine with an ellipse as a part of its male rotor: US, A4890992[P]. 1990-01-02.