过渡支撑条件下扇环形板应力分析

，

(河北科技大学 机械工程学院， 河北 石家庄 050018)

扇环形板壳是一种广泛应用于化工、机械、能源及动力等领域的结构部件[1]。在工业生产中，采用扇环形截面的容器或者管道可以有效节约空间[2]。因此，扇环形板的静力学分析与设计就成了一项重要的研究内容[3-4]。大直径热交换器(如核电工业中的蒸汽发生器)管板是整个设备的关键部件，由于承受较高的压力和温度，大直径热交换器的管板厚度很大，设计、制造十分困难[5-7]，因此开展大直径蒸汽发生器管板的设计与制造方法研究十分必要，国内外的研究人员对此进行了一系列的研究[8-11]。基于此，2014年刘庆刚[12]等人提出了一种采用扇环形组合管板解决大直径管板设计、制造问题的方法，可以有效减小管板的当量直径，降低设计、制造难度。然而，GB 150.1～150.4—2011《压力容器》[13]和美国ASME VIII-1《压力容器建造规则》[14]等具有广泛影响的标准中均未对具有扇环形管板结构容器的设计和制造方法做出规定。因此，针对具有扇环形管板的容器开展研究，对于推进大直径换热设备管板设计和制造技术的进步，完善国家压力容器标准具有一定的意义。

采用扇环形组合管板替代整块圆形管板的技术关键在于明确扇环形板在各种载荷作用下的力学响应，国内外学者对扇环形板提出了各种解析求解方法，但仅限于在直边或圆弧边简支和固支的边界条件下。钱民刚等人[15-16]给出了扇形板、环形板弯曲问题的Fourier-Bessel级数解。Aghdam M M等人[17]应用扩展的康托诺维奇方法对扇形薄板的弯曲变形和应力进行计算，数值计算结果表明该方法精度较高。钱民刚等人[18]利用加补充项的Fourier-Bessel双重级数的位移模式，给出了沿直边简支的环扇形弯曲问题的级数解。陈聪等人[19-20]采用Shannon小波配置法并结合精细积分法分析了周边固支扇形板的静力学问题。

现有计算方法仅能计算周边简支与固支的扇环形板，且计算方法复杂，难以在工程设计中应用，对于处于简支与固支之间的过渡支撑也没有相应计算公式，缺乏有效的分析方法。然而，在机械、化工生产等领域经常会出现板与板之间既不是简支，也不是固支的过渡支撑情况。基于此，文中以扇环形板厚h=60 mm、扇环形板夹角(简称扇形角)Ф为45°和60°、支撑竖板厚度逐渐变化的多组模型为研究对象，采用有限元软件ANSYS进行数值模拟，研究不同支撑条件下扇环形板的应力分布状况。

1 扇环形板过渡支撑模型及参数

扇环形板结构模型见图1。为了研究扇环形板在介于简支和固支之间过渡支撑条件下的应力分布，按照图1建立了有限元模型，见图2。图1中，δ1为直边支撑竖板厚度，δ2为圆弧边支撑竖板厚度，R1为扇环形板内半径，R2为扇环形板外半径。扇环形板承受均布载荷时，如果δ1和δ2无限趋近于0，扇环形板在支撑部位受到的竖板附加弯矩也趋近于0，此时支撑条件相当于简支。同理，当δ1和δ2趋向无穷大时，支撑条件相当于固支。因此，通过改变δ1/h和δ2/h的比值，可以得到介于简支和固支之间的过渡支撑条件。通过建立不同的有限元模型，可分析过渡支撑条件下扇环形板的应力变化规律。为了更加准确地分析直边和圆弧边约束对扇环形板应力分布的影响，分别建立仅有直边和圆弧边支撑的模型进行分析。

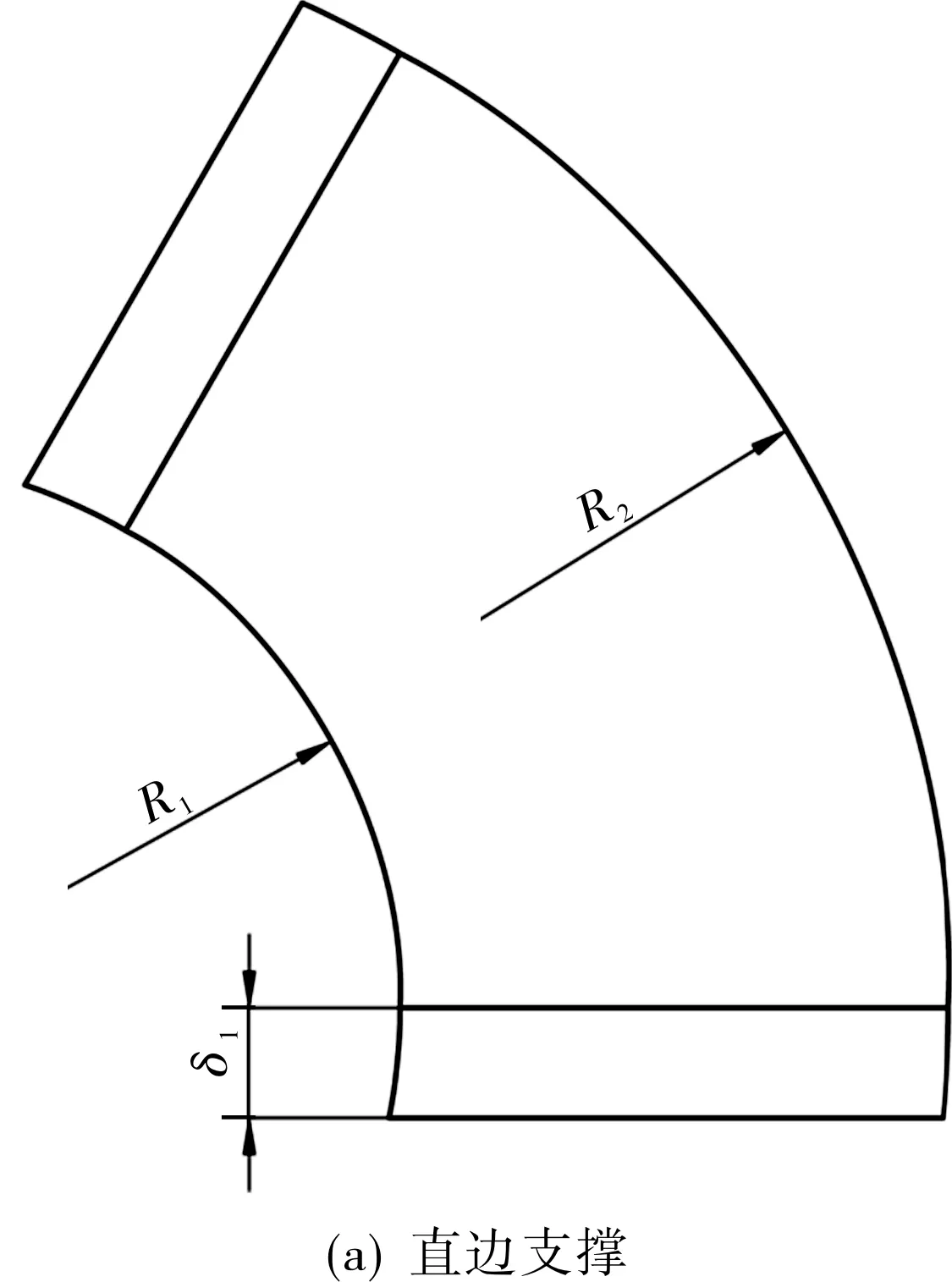
图1 扇环形板结构模型

图2 扇环形板有限元模型

为了研究不同支撑竖板厚度和扇形角对扇环形板等效应力的影响，文中设定h=60 mm，Ф为45°和60°，δ1为5～140 mm，δ2为5～160 mm，δ1、δ2间隔均为5 mm。扇环形板、直边支撑、圆弧边支撑材料均选用Q345R，其弹性模量为2.01×105MPa、屈服强度为345 MPa、抗拉强度为510 MPa[13]，常温下许用应力见表1[13]。

表1 Q345R常温下不同板厚许用应力

2 扇环形板过渡支撑有限元模型

2.1 分析路径

根据扇环形板的对称性，当仅有直边支撑时，选取如图3a所示的路径，简称路径a；仅有圆弧边支撑时，选取如图3b所示的路径，简称路径d。通过分析路径a和路径d上的应力分布情况，了解模型对外载荷的响应，研究扇环形板外表面上的应力分布情况。

2.2 载荷与约束

准确地识别、定义载荷，是得到精确的有限元结果的关键。为了消除支撑板变形对扇环形板应力分布的影响，仅在扇环形板的内表面施加2 MPa的压力，支撑竖板的延长端面施加固定约束。

3 扇环形板过渡支撑有限元结果分析讨论

图3 扇环形板有限元分析路径

有限元数值模拟得到了Ф为45°和60°时路径a和路径d在不同支撑竖板厚度条件下的等效应力分布状况，分别见图4、图5。

图4 Ф=45°时扇环形板不同路径上等效应力

图5 Ф=60°时扇环形板不同路径上等效应力

由图4a可知，扇形角Ф=45°时，路径a上等效应力的变化趋势为先减小后增大，然后再减小。支撑边厚度较小时，最大等效应力出现在路径起始点处。随着厚度的增大，距离路径终点40 mm位置的等效应力增加较为迅速。由图4b可以看出，由于路径d选取在对称中线上，路径上的应力几乎完全对称，因此路径d上的最大应力均出现在距路径两端点20 mm左右的位置。

由图5a可知，扇形角Ф=60°时，路径a上最大等效应力均出现在起点处，最小值处于路径终点处。在远离路径起点和终点的部位，应力基本保持不变。这与扇形角Ф=45°时，路径a上的应力分布情况不同，表明扇形角对仅直边支撑条件下的应力分布具有较大的影响。由图5b可以看出，扇形角Ф=60°时路径d上应力的变化规律与Ф=45°时一致，表明扇形角Ф对圆弧边支撑条件下扇环形板的应力分布影响不大。

图4和图5中，当支撑竖板的厚度较小(δ1=5 mm或δ2=5 mm时)或较大(δ1=140 mm或δ2=160 mm)时，应力随着支撑竖板厚度的变化较小，表明支撑条件接近于简支或固支状态。当支撑竖板厚度处于两者之间时，随着支撑竖板厚度的变化，路径a和路径d上的总体应力变化较大，表明扇环形板处于过渡支撑状态。为了进一步研究过渡支撑条件下支撑竖板厚度对扇环形板应力的影响，取每个支撑竖板厚度下路径a和路径d上等效应力的最大值绘制成曲线，见图6。

图6 不同支撑竖板厚度下扇环形板路径等效应力最大值

由图6可知，对于直边支撑模型，不同扇形角时，2条等效应力最大值曲线相距很远，说明扇形角对直边支撑条件下的扇环形板应力影响较大。这是由于直边支撑时，扇环形板的跨度随着扇形角的增大而增大，而路径a受到的约束随扇环形板跨度的增大而变弱，因此扇形角对直边支撑影响较大。圆弧边支撑的2条等效应力最大值曲线基本重合，这是因为圆弧边支撑时，路径d到两支撑边的距离不随扇形角的增大而增大，所受到的约束也不随扇形角的增大而变弱，因此扇环形板的应力不随扇形角的增大而增大。

对于2个扇环形角度的模型，无论何种支撑条件，随着支撑竖板厚度的增大，最大等效应力首先维持不变(A区域)，然后迅速下降。当支撑竖板厚度较大时，最大等效应力几乎不再随着厚度的增加而降低(B区域)，这一系列变化表明扇环形板分别处于简支(A区域)、过渡支撑和固支(B区域)3种支撑条件下。

假设2个相邻支撑竖板厚度对应的等效应力最大值变化不超过0.2%时可认为应力不再发生变化，支撑条件进入简支或固支，得到的过渡支撑与简支、固支之间的临界支撑竖板厚度分别见表2和表3。

表2 简支与过渡支撑临界支撑竖板厚度

表3 过渡支撑与固支临界支撑竖板厚度

4 结语

基于有限元分析方法，建立了不同支撑条件下扇环形板的静态分析模型，选用不同的支撑竖板厚度分别模拟固支、过渡支撑和简支条件，采用ANSYS软件进行数值模拟。分析认为，无论是直边支撑还是圆弧边支撑，随着支撑竖板厚度的增大，扇环形板依次处于简支、过渡支撑和固支状态。扇形角对直边支撑条件下扇环形板的应力分布影响较为显著，但对圆弧边支撑条件下扇环形板的应力分布影响较小。当支撑竖板厚度与扇环形板厚度比值小于0.2时，扇环形板近似进入简支状态；当支撑竖板厚度超过扇环形板厚度的2倍时，扇环形板近似进入固支状态。

文中提出了一种扇环形板过渡支撑条件的应力分析方法，其分析结果可为不同扇形角的过渡支撑扇环形板应力分布状况研究提供一定的参考。

参考文献：

[1] Seok J，Tiersten H F. Free vibrations of annular sector cantilever plates. Part 1：out-of-plane motion[J]. Journal of sound and vibration，2004，271(35)：757-772.

[2] 宫继双，范育新，张靖周.扇环形截面管内爆震波特性研究[J].工程热物理学报，2010，31(6)：1077-1079.

GONG J S，FAN Y X，ZHANG J Z. Investigation of detonation wave in annular-sector tube[J]. Journal of engineering thermophysics，2010，31(6)：1077-1079.

[3] 章本照，张金锁.扇环形截面弯曲管道内的粘性流动[J].空气动力学学报，2000，18(2)：216-220.

ZHANG B Z，ZHANG J S. Viscous flow in curved annular sector duct[J]. Acta aerodynamica sinica， 2000，18(2)：216-220.

[4] 石先杰，史冬岩，李文龙，等.任意边界条件下环扇形板的静动态特性分析[J].机械设计与制造，2013(12)：181-184.

SHI X J，SHI D Y，LI W L，et al. Static and dynamic characteristics analysis of annular sector plates with general boundary conditions[J]. Machinery design & manufacture，2013(12)：181-184.

[5] 杜南麟，陈中灼，陈富彬.三门核电厂2号机组蒸汽发生器管板钻孔偏差原因分析及问题处理[J].核动力工程，2014，35(3)：76-79.

DU N L，CHEN Z Z，CHEN F B. Disposition of drilling deviation for steam generator tubesheet in Sanmen NPP unit 2[J]. Nuclear power engineering，2014，35(3)：76-79.

[6] 许文镜，刘鸣宇，王小刚.百万千瓦级核电蒸汽发生器管子-管板焊接工艺研究[J].热加工工艺，2012，41(23)：170-173.

XU W J，LIU M Y，WANG X G，et al. Welding procedure for tube to tube sheet weld of million-kilowatt-class nuclear power steam generator[J]. Hot working technology，2012，41(23)：170-173.

[7] 李海龙，王庆，徐宇，等.蒸汽发生器管板孔桥超差情况下的结构安全性分析[J].原子能科学技术，2014，48(11)：2028-2032.

LI H J，WANG Q，XU Y，et al. Structural safety analysis on tube sheet with deviated holes in steam generator[J]. Atomic energy science and technology，2014，48(11)：2028-2032.

[8] 倪鹏，惠虎，王晓东，等.蒸汽发生器管板液压胀管数值模拟研究[J].核动力工程，2015，36(5)：204-207.

NI P，HUI H，WANG X D，et al. Numerical simulation of hydraulically expanded tube-to-tubesheet joints in steam generator[J]. Nuclear power engineering，2015，36(5)：204-207.

[9] 丘振生，黄腾飞，杨春乐.蒸汽发生器管子管板封口焊缝质量影响因素分析[J].焊接，2015(3)：1-6.

QIU Z S，HUANG T F，YANG C L. Analysis of influence factors on tube-to-tube sheet seal weld quality of steam generator[J].Welding & joining，2015(3)：1-6.

[10] Chi Bum Bahn，Saurin Majumdar，Ken E Kasza，et al. Leak behavior of steam generator tube-to-tubesheet joints under creep condition：Experimental study[J]. International journal of pressure vessels and piping，2013，101：55-63.

[11] Zhu L K，Qiao L J，Li X Y，et al. Analysis of the tube-sheet cracking in slurry oil steam generators[J]. Engineering failure analysis，2013(34)：379-386.

[12] 刘庆刚，王珺，郭彦书，等.扇环形半圆截面圆筒应力分布规律研究[J].河北科技大学学报，2014，35(4)：370-375.

LIU Q G，WANG J，GUO Y S，et al. Study of stress distribution principle of an annular sector semicircular cross section vessel[J]. Journal of Hebei university of science and technology，2014，35(4)：370-375.

[13] 压力容器：GB 150.1～150.4—2011[S].

Pressure vessel：GB 150.1～150.4—2011[S].

[14] ASME锅炉及压力容器规范：第VIII卷压力容器建造规则第一分册[S].

ASME boiler and pressure vessel code：rules for construction of pressure vessels(VIII) Division 1[S].

[15] 钱民刚，严宗达.扇形板的富里哀-贝塞尔级数解[J].应用数学和力学，1985，6(4)：359-376.

QIAN M G，YAN Z D. Solution of sector plate by Fourier-Bessel series[J]. Applied mathematics and mechanics，1985，6(4)：359-376.

[16] 钱民刚，严宗达.环形板的Fourier-Bessel级数解[J].北京建筑工程学院学报，1990(1)：50-57.

QIAN M G，YAN Z D. Solution of annular plate by Fourier-Bessel series[J]. Journal of Beijing institute of civil engineering and architecture，1990(1)：50-57.

[17] Aghdam M M，Mohammadi M，Erfanian V. Bending analysis of thin annular sector plates using extended Kantorovich method[J]. Thin-walled structures，2007，45(12)：983-990.

[18] 钱民刚，严宗达.沿直边简支的环扇形板的Fourier-Bessel级数解[J].工程力学，1995，12(2)：22-29.

QIAN M G，YAN Z D. Solution of annular sector plate simply supported along radial edges by Fourier-Bessel series[J].Engineering mechanics，1995，12(2)：22-29.

[19] 陈聪，张领，卿光辉.周边固支环扇形板静力学问题的小波方法[J].中国民航大学学报，2009，27(1)：60-64.

CHEN C，ZHANG L，QING G H. Wavelet method of static solution for annular sector plate with four sides clamped[J]. Journal of civil aviation university of China，2009，27(1)：60-64.

[20] 钟万勰.结构动力方程的精细时程积分法[J].大连理工大学学报，1994，34(4)：131-136.

ZHONG W X. A precise time-integration method for structure dynamics[J]. Journal of Dalian university of technology，1994，34(4)：131-136.