基于Laplace小波相关滤波的周期性冲击故障特征提取
高洪波
(辽宁省交通高等专科学校机电工程系,辽宁沈阳110122)
0 引言
在齿轮、轴承等广泛应用的旋转机械中,冲击类故障占据了非常高的比例,如动静件间的周期性碰撞、过大齿侧间隙的轮齿啮合冲击、缺陷轮齿或轴承运行时的瞬时冲击等。因此,针对普遍存在的周期性冲击故障进行监测与诊断,对机械设备安全稳定运行具有重要意义。
故障特征提取是故障诊断的关键,而对于周期性冲击故障,检测故障信号中冲击响应的存在及其发生频率至关重要。以齿轮系统为例,故障部位的周期性脉冲力会激发齿轮系统固有频率的冲击响应,并对啮合振动产生幅值调制和相位调制,调制频率一般为故障部位的运行频率,如齿轮轴或轴承的旋转频率、碰磨发生的频率等。但故障信号冲击成分一般具有持续时间短、信噪比低等特点,极易淹没在背景噪声中,难以识别。
本文鉴于Laplace小波与冲击响应的相似性,提出基于Laplace小波相关滤波的周期性冲击故障特征提取方法,并以轴承故障为例进行有效性验证。
1 Laplace小波
Laplace小波由G.Strang[1]等首次提出,通过对二阶欠阻尼系统进行拉式反变换得到。Laplace小波是一种在复数空间内呈螺旋形单边衰减的复小波,一般应用其实数解析形式,表达式为:
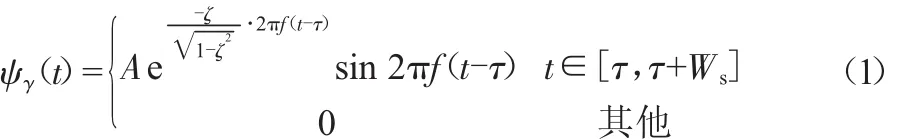
其中,参数空间γ(f,ζ,τ)决定了小波函数的波形特征。式中,f∈R+为尺度参数,表示小波振荡频率;ζ∈[0,1]⊂R+表示粘滞阻尼比;τ∈R为时移参数;系数A用来归一化小波函数;Ws表示小波支撑区间的宽度。
2 Laplace小波相关滤波方法
令Laplace小波的参数空间γ(f,ζ,τ)形成的集合为:

设离散的参数空间为Γ=F×Z×T,则Laplace小波函数库为由一组ψγ构成的集合Ψ,它满足:
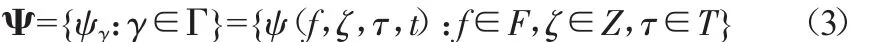
式中,ψγ为小波函数库的一个原子。
设振动系统采集的输出信号为x(t),相关滤波法[2]利用小波函数库中各小波原子与信号x(t)的内积来估计它们之间的相似性。首先,将小波函数在时域离散成与x(t)相同长度和时间分辨率的向量,其相关性可用内积或点积表示为:
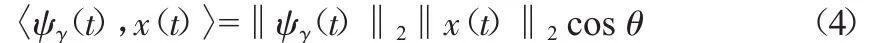
其中,夹角θ是表示相关性的度量参数,若两向量完全线性相关,则夹角θ=0。一般用相关系数kγ来量化夹角的大小:

则有,kγ∈[0,1]。
由于γ∈Γ,那么kγ是由F×Z×T的大小决定的多维矩阵。小波相关滤波法辨识模态参数,就是在小波函数库Ψ中寻找与x(t)的相关系数最大的原子,最大的kγ对应的(fˆ,ζˆ,τˆ)即为与x(t)最为匹配的小波函数参数。
设τ时刻选择不同的f和ζ时,获得的F×Z个相关系数kγ的最大值为kγτ,对应的频率和阻尼参数分别为 f¯、ζ¯,即k(τ)=那么,相关滤波就是在各时移参数τ对应的
k(τ)集合上,寻找其最大值所对应的小波原子ψγ的频率和阻尼。在相关滤波结果中,相关系数的峰值时刻,即原信号中脉冲响应发生的位置,而且可以获得对应的Laplace小波频率和阻尼比。
3 实验分析
采用美国凯斯西储大学(Case Western Reserve University,CWRU)网站开放的轴承运行状态测试数据[3]进行验证。实验轴承型号为SKF6205,采集了轴承在0 kW、0.746 kW、1.492 kW和2.238 kW四种载荷下,正常状态、外环故障、内环故障和滚动体故障四种状态的运行数据。本文选用其中1.492 kW载荷下的轴承外环故障数据,故障为直径0.007″的微小坑点,主轴转速为1 750 r/min,采样频率为12 000 Hz。根据轴承设计参数,外环故障特征频率为3.584 8倍主轴频率,约为104.5 Hz。随机截取2 000点的故障振动信号样本,时域波形如图1所示。

图1 轴承外环故障振动信号
根据幅值谱图,故障信号在2 500~3 500 Hz的频带内波峰幅值最高,说明故障脉冲激发了该频段的共振响应。将相关滤波参数范围设置为F={2 500:1:3 500}、Z={0.01:0.02:0.21}、T={1/fs:1/fs:2 000/fs},获得的相关滤波结果如图2所示。与图上相关系数各个最大值对应的即是各脉冲响应发生时刻。为了解故障冲击的调制频率,对图2的相关系数进行解调分析,得到包络解调谱如图3所示。在该谱图上可以观察到105 Hz的调制频率谱峰,与外环故障频率理论值近似相等,可以判断该轴承运行信号中包含外环故障信号成分。
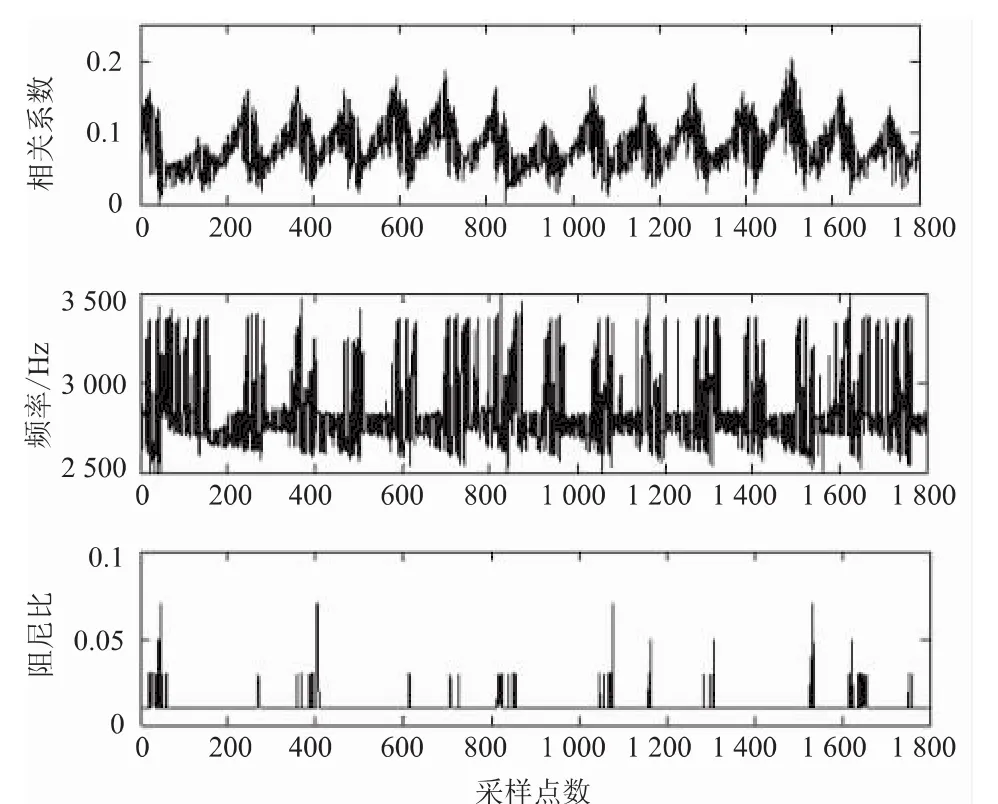
图2 故障信号Laplace小波相关滤波结果
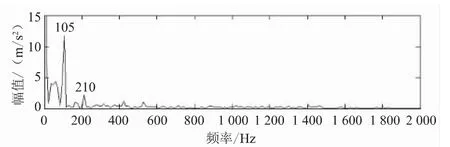
图3 相关滤波系数的包络解调谱
4 结语
故障振动信号中的冲击响应时刻、调制频率等特征信息是冲击故障诊断的有效依据。本文提出的基于Laplace小波相关滤波的故障特征提取方法,利用幅值谱分析方法确定相关滤波的频率范围,对相关系数进行包络解调获得故障特征频率。实验表明,通过本文方法,不但可以有效去除冲击类故障信号中的噪声,获取特征信息,而且缩小了频率搜索范围,提高了算法效率。
[1] Strang G,Nguyen T.Wavelets and filter banks[M].Wellesley,MA:Wellesley Cambridge Press,1996:71-85.
[2]何正嘉,訾艳阳,张西宁.现代信号处理及工程应用[M].西安:西安交通大学出版社,2007.
[3]The Case Western Reserve University.Bearing data center[EB/OL].(2009-08-06).http://www.eecs.cwru.edu/laboratory/bearing.

