电动机轴承处振动的在线检测方法分析
冷 宇 李 栋
(1.上海科学技术职业学院,上海201800;2.华域电动系统有限公司,上海201203)
0 引言
电动机是现代化工业时代必不可少的生产动力提供设备,其在工业、农业、商业领域都有广泛应用。对于电动机故障的检测和预防可以为生产减少损失,并避免不必要的安全事故。在电机故障检测中,最重要也是最常用的数据就是电机轴承的振动数据,为了实现电机轴承的振动数据(加速度、速度、位移)检测,本文采用了ICP传感器(加速度传感器)。为了实现本文设计的良好拓展性,将处理后的数据使用RS485通信协议与上位机进行数据交换,从而进一步实现更多功能的数据分析,以进一步完善振动检测。
1 方案介绍
本文所设计的检测装置硬件电路主要分为六大块,分别为辅助电源电路、DSP控制电路、RS485通信电路、信号调理电路、报警电路、LCD显示电路,其功能框图如图1所示。

图1 功能框图
2 硬件电路设计与仿真
本小节主要介绍硬件电路的设计。由图1可以看出来硬件电路主要分为五大块,即辅助电源、DSP控制电路、RS485通信电路、信号调理电路和LCD显示与报警电路。
辅助电源主要实现对各个电路模块的供电,整个系统需要的电源有+5 V、-5 V、4 V、恒流源和隔离+5 V。由于本文的ICP传感器是使用恒流源供电,选择LM317芯片组成恒流源。本文所选择的ICP传感器正常工作时所需要的外接恒流源需提供2~20 mA电流,这里设从1号管脚ADJ所流出的电流为Iadj,由于Iadj≪Icc,所以忽略Iadj,有:

所以,调节电阻R23即可得到想输出的恒流值。
主控芯片选择TMS320F2812。通信电路设计,本文选择了RS485通信协议。使用MAX491芯片作为收发器实现通信,均采用光耦进行隔离。
压电式ICP传感器内置电荷放大器电路模块,直接输出电压,无需设计专门的电荷放大器,使用简单,抗干扰性能好,可长线使用,其型号为JM411-22。
本文使用二阶低通巴特沃斯滤波器,截止频率理论计算:

U2A运放实现了隔直和电压抬升的作用,设输入电压为U2A,输出电压为U2Ao,则有公式:

U1A运放实现了比例缩小,设输入电压为U2B,输出电压为U2Bo,则有公式:

为了验证电路设计的可靠性和稳定性,本文使用Multism对设计电路进行了仿真,仿真结果如图2所示。

图2 仿真结果
3 软件算法设计
软件控制主要分为五大块:小波消噪、频域滤波、去除趋势项、数字积分和信号显示,用于实现对采样信号的处理。软件算法框图如图3所示。
下面详细介绍各个模块的作用与功能。
3.1 小波消噪
直接采集的加速度信号具有较多的噪声信号,这些信号的存在会给信号处理带来较大误差,为使速度信号和位移信号具有较高的准确度,则需进行消噪,本文选用小波消噪法。
3.1.1 小波消噪的数学模型及基本方法
首先,为了方便建立数学模型,必须对噪声信号作出三个假设:(1)噪声经小波变换后大多数小波系数为零或近似为零;(2)噪声均匀地分布在所有系数中;(3)噪声水平不是太高。
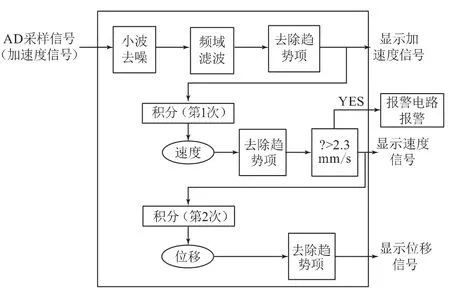
图3 软件算法框图
设观测得到的数据:

由公式可知,观测数据是由真实信号g和噪声ε叠加而成,f=g+ε为向量形式。在理想情况下,εi需要满足以下三点:(1)正态噪声;(2)不相关噪声;(3)方差为常量。
由于现实中较难达到要求,所以必须将假设条件放宽,否则不能满足实际测量的需要。最终目的是使用观测到的f,得到估计的g。设观测数据由小波变换后得:

设W(·)和W-1(·)分别表示小波变换和逆变换算子,则小波消噪的过程可定义为:
(1)w=W(f)——小波变换;
(2)wt=D(w,t)——对小波系数进行非线性处理,以滤除噪声;
(3)gˆ=W-1(wt)——小波逆变换。
非线性滤波算子D(·,·)为去噪问题的关键,通过选择不同的W(·)和D(·,·),则有多种去噪的办法。小波消噪的关键在于第(2)步——按照一定的准则修改小波系数,从而在损失较小信号的前提下达到去噪效果。目前小波消噪有贝叶斯法和非贝叶斯法,一般采用非贝叶斯法,非贝叶斯法大致可分为三种:(1)模极大值重构滤波法消噪;(2)空域相关滤波消噪;(3)小波阈值滤波消噪。
对比以上三种滤波算法可知,小波阈值滤波消噪效果相对较好,实现也较简单。本文采用该方法,仅需改变阈值即可得出不同的滤波效果。
3.1.2 小波阈值滤波消噪
有用信号经过小波变换后的小波系数具有幅值大、数量少的特点,并且包含信号的重要信息,而噪声的小波系数则幅值较小。正是基于以上特点,在不同尺度上选取不同阈值,将小于该值的小波系数归零,保留大于阈值的系数,就可以实现去噪,最后进行逆变换,实现信号复原。
Donoho对阈值滤波提出了两个前提条件:
(1)光滑性——在大概率情况下,gˆ至少跟g有同样的光滑度;
(2)适应性——gˆ是最小均方差估计。
由条件(1)可得,当N→∞时,下式近似为1的概率成立:

式中,C1为常数,小波域则有式(8)的成立。

式中,1≤i≤N为位置,j为尺度;θj,i为真实信号在尺度j上的第i个小波系数。
对于条件(2),可以理解为对式(9)求最小值,与对式(10)求最小值互为等价,Donoho证明,此时gˆ、θˆ必须满足式(11)。

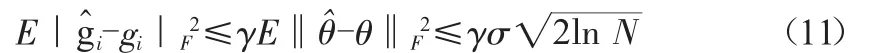
由式(11)可知,对于任何,取θj,i=0,将满足式(10)。这相当于认为当,θj,i由噪声所产生,因此,可取阈值为
阈值滤波有硬阈值滤波和软阈值滤波之分,下面分别介绍两种滤波的方法和步骤。
硬阈值滤波消噪的步骤为:
(1)对信号求小波变换;
(2)除了最粗尺度信号外,对细节信号作阈值处理,阈值当某位置小波变换值大于阈值时,保留原值,否则置零,用公式表示为:

(3)利用小波变换重构,求出信号的滤波值。
软阈值滤波消噪的步骤为:
(1)对信号求小波变换;
(2)除了最粗尺度信号外,将各细节信号作阈值处理,阀一旦出现阈值小于小波变换值时,向着减小系数幅值的方向做一个收缩t,否则置零,用公式表示为:
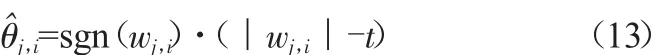
式中,sgn(x)为符号函数。
(3)进行小波变换重构,求出信号的滤波值。
综上所述,如果要实现整个算法,则需知道噪声的方差,噪声标准差σ的估计已经由Donoho给出。
阈值和阈值函数是小波阈值滤波算法中的两个基本要素,阈值对滤波效果具有较大影响,因此阈值的确定较为关键,而目前的文献中给出了很多阈值的确定方法。
使用Matlab仿真,结果如图4所示。通过仿真可以看出,小波降噪具有良好的去噪效果。
3.2 FFT滤波
消噪后的信号仍存在干扰信号,所以需要做滤波处理,本设计采用FFT滤波(频域滤波)。FFT滤波是基于FFT快速傅里叶算法,将采样信号进行离散傅里叶变换,分析频谱,并根据要求将滤除频率成分设置为零,最后采用IFFT(傅里叶逆变换)快速算法恢复出时域信号。该方法的频域表达式为:
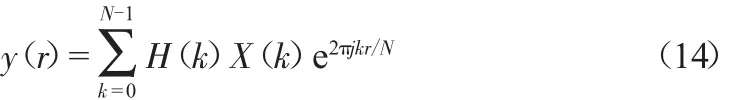

图4 仿真结果
式中,X为输入信号X的离散傅里叶变换;H为滤波响应函数。
设fu为上限截止频率,Δf为频率分辨率,本文选择低通滤波器,即FFT滤波中采用低通滤波器滤波,其频率响应函数如下:
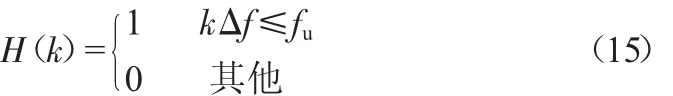
3.3 去除趋势项
在实际测量中,由于现实环境的不断变化,会产生零点漂移、传感器测量特性改变等等不良因素。而这些因素会导致测量结果偏离基线,并随时间而改变,这一现象被称为趋势项。而数据一旦进行积分,趋势项所带来的影响则不可忽视,若是再二次积分,则有可能使积分的结果完全失真。本文选用多项式最小二乘法,原理如下:
将{xk}(k=1,2,3,…,n)设为实际所获得的振动信号的采样,因为在现实中是固定步长进行采样,令Δt=1为采样步长时间,并设如下多项式:

由xˆk与xk的差值平方最小可求aj(j=0,1,2,…,m),即:

由式(16)可得:

通过对式(18)求解,则可以求出m+1个待定系数aj(j=0,1,2,…,m)。若m=0,则可解得:

若m=1,则可解得:

当m≥2时,也可以同理算出。值得注意的是,实际采样中一般取m=1~3来去除趋势项。
使用Matlab进行仿真,仿真结果如图5所示。
3.4 数字积分
在经过一系列的软件信号调理之后,接下来就需要进行数字积分,以求出速度与位移信号,并将位移信号与设定的保护值实时比较,一旦发现比设定值大,那么将会进入中断,执行报警程序。

图5 仿真结果
本文所设计的数字积分采取简单的梯形法。梯形法是将一个被积函数的曲线分成很多个小区域,并将分割的小区域看为一个个梯形。令x(i-1)和x(i)为相邻的两个点,Δt为积分步长,则可得到数学表达式:

其中,k=1,2,3,…,N。
使用Matlab对梯形法积分算法进行仿真,得到如图6所示仿真结果。

图6 梯形法积分仿真结果
4 结语
本文总结并给出了电机轴承处振动在线监测设备的硬件和软件设计,并给出小波消噪的基本算法,实现对振动数据的监测,从而最终实现对电机轴承的保护,并将相关数据上传至上位机,以便上位机实现对大数据的分析。
[1]羊初发.基于EMD的时频分析与滤波研究[D].成都:电子科技大学,2009.
[2]杨君,吕镜清.FFT滤波误差分析[J].通信技术,2010,43(6):235-237,240.
[3]朱可恒.滚动轴承振动信号特征提取及诊断方法研究[D].大连:大连理工大学,2013.
[4]HAMMAN J,VAN DER MERWE F S.Voltage harmonics generated by voltage-fed inverters using PWM natural sampling[J].IEEE Transactions on Power Electronics,1988,3(3):297-302.
[5]王赛男,邢冬梅.基于MATLAB的小波阈值滤波与应用[J].软件,2015,36(10):102-104.

