基于FFD与网格重构的飞翼无人机外形优化设计

王荣 白鹏

摘要：为了使气动优化适应外形大尺度变化和外形高效参数化的需要，将外形高效参数化建模方法（FFD）与适合外形剧烈变化的网格重构方法相结合，对飞翼无人机外形完成了气动优化设计。外形参数化建模采用自由变形法（FFD），网格生成基于贴体笛卡儿自动网格重构技术，通过优化设计使飞翼无人机的气动性能得到了有效提升，布局升阻比增加了了.9%0优化结果表明，基于该技术的气动优化设计方法对大尺度变化外形具有良好的适应性。

关键词：自由变形法;网格重构;飞翼布局;无人机;优化设计

中图分类号：V211+.3 文献标识码：A

近些年应用潜力巨大的无人机得到了快速发展。飞翼无人机具有较好的性能，是一种应用价值高的布局形式，对其气动性能开展优化研究具有实际意义。

在气动布局优化设计过程中，采用CFD技术数值求解BANS方程进行气动性能精细预测的方法，在外形参数化建模和网格自动化生成方面面临很大的挑战。尤其是对工程应用，高效快速和适应性强的外形和网格自动构建方法是气动优化的难点，如适用外形大位移、大变形的可靠方法。

几何参数化方法包括离散点方法、偏微分方程法、多项式和样条法、基矢量法、域元素法、解析法，CAD方法和自由变形法CFree-Form Deformation，FFD等多种技术[1～4]。其中FFD方法是一种高效建模方法，其特征是基于變形造型的思想，不需要对基准外形进行直接建模，只需构造基准外形与空间控制点的映射关系，改变空间控制点的位置实现外形几何变形。FFD方法操作简单，能有效降低外形参数化难度，并且对拓扑形式没有要求，基准外形可以具有任意形状，因此适于复杂外形参数化造型。

气动优化时外形改变后流场网格常采用变形的方法自动生成[5～7]，对于外形变化幅度小，网格变形方法能够适应，对于大位移、大变形，甚至变几何拓扑问题，网格变形方法往往会失效，使网格扭曲甚至产生负体积，不能保证网格质量，通常难以应用。这便需要采用适应性更好的网格重构方法。

本文将FFD方法与网格重构方法相结合，对飞翼无人机外形采用FFD变形技术进行参数化建模，结合基于贴体笛卡儿网格的流场网格自动重构技术，实现了对大尺度变化外形具有良好适应性的气动优化设计方法。

1 外形参数化方法

1.1 基于FFD的外形建模方法

FFD自由变形法起源于计算图形学领域，由Sederberg和Parry于1986年提出，该方法假定物体有很好的弹性，在外力的作用下易于发生变形。造型时构造一个由控制点构成的控制框架，将物体置于框架中，当框架受外力作用而变形时，物体的形状也随之改变[2]。

根据所使用的基函数的不同，FFD方法包括基于Bezier的FFD方法、基于B样条的FFD方法以及基于非均匀有理B样条（Non-Uniform Rational B-Spline，NURBS）的FFD方法[8]。

对不同的基函数，FFD控制框架中任意点的笛卡儿坐标X（s，t，u）都可以统一表达为：式中：s，t，u为控制体局部坐标（参数坐标），且0≤s，t，u≤1，P_i，j，k为控制顶点笛卡儿坐标，三个方向的控制顶点数目分别为l+1、m+1、n+1。

对基于Bezier的FFD方法，采用Bernstein基函数：

对基于B样条的FFD方法，采用B样条基函数：

R_i（s）=N_i，kk（s）（3）

对基于NURBS的FFD方法，采用NURBS基函数：式中：B_lⁱ（s）为1次（l+1阶）Bernstein多项式基函数，N_i，k（s）为k次B样条基函数（k≤1），ω_i为对应控制点的权因子，基函数值可通过调节权因子来改变，由于NURBS与B样条采用相同的基函数，其性质与N_i，k（s）相关。

B样条基函数N_i，k（s）通过德布尔-考克斯递推公式求解[9]：

式（5）说明高次B样条函数可用低次的B样条函数递推计算，ti是沿参数轴分布的节点值。

FFD方法与物体几何形体的表达方式无关，无论几何形体是如何表达的，FFD都是借调整控制框架顶点的空间位置来改变几何形体的形状，而不是直接进行物体表面的位移，因此具有很强的通用性，可以用于任意复杂外形参数化。

除此之外，FFD方法突出的优点还有[9]：变形能力强，可以保持几何原有连续性、光滑性;操作简单，能有效降低外形参数化难度，不需要对初始外形进行拟合，适用于任意复杂外形物体;能用较少的设计变量光滑地描述曲线、曲面、三维几何体的几何外形;可整体也可局部使用，局部使用时能方便地应用于局部外形修形设计，并且可保持物体间跨界导矢以及更高阶导矢的连续性。

正是基于这些特点，FFD方法不仅在计算机几何建模与动画设计中得到了非常广泛的应用，目前也已被应用于飞行器气动优化设计研究中。

1.2 飞翼外形参数化建模

飞翼无人机外形如图1所示，翼平面为双后掠的隐身布局形式，初始外形采用参考文献[10]中的方法生成。

基于FFD的飞翼无人机外形参数化建模过程如图2所示，以半模外形为例，首先建立一个控制体包络将需要参数化的飞翼无人机初始外形置于包络中，并求出在控制体中的翼面外形坐标点对应的局部坐标;然后移动控制体上的控制点，形成控制体新的框架位置;最后根据新的控制点位置和参数坐标，由式（1）得到相应变化后的外形。

计算翼面外形点所对应的局部坐标实际上是一个求解逆映射的问题XO X（s，t，u），一般情况下，该问题需要求解s，t，u三个变量的非线性方程组，通常采用三变量Newton迭代法计算，也可以采用区域分割法直接对控制体进行逐级剖分解算[2]。

图中FFD变形框架采用剪切变形的方式完成，只需改变一个后掠角参数就可以实现外形整体大幅变化。相对参考文献[10]中基于外形特征的参数化建模方法，对此类飞翼外形，基于FFD变形参数化建模方法，建模效率高，鲁棒性和灵活性更好，尤其是参数范围选取不受限制。而基于外形特征解析的方法，由于参数的几何相关性，参数变化范围不能随意选取，否则不能得到合理的平面形状[10，11]。

2 基于网格重构的气动优化方法

2.1 网格重构方法

网格自动化构建是气动外形优化流程中必要的步骤。气动优化过程中，外形改变后流场网格可以基于变形策略采用动网格技术通过变形方法自动生成[5-7]，也可以采用网格重构的方法重新生成计算域的网格。网格变形方法通常仅对外形变化幅度小的情况适用，对大位移、大变形、甚至变几何拓扑问题，如以上飞翼平面大幅改变的情况（如图2所示），网格变形方法往往会失效，使网格扭曲甚至产生负体积，不能保证网格质量，通常难以应用。网格重构的方法能够适应外形剧烈变动的情形，网格重构的关键在于网格的自动化重构。本文采用基于笛卡儿网格划分技术的网格自动重构的方法。笛卡儿网格方法采用“空间到边界”的网格划分策略[12]，具有网格构建快速、自动的特点，是一种高效的流场网格剖分方法。网格生成过程中，采用了基于部件建模和几何特征信息的局部加密技术，采用投影方法生成贴体网格，将投影至物面的柱形网格进一步划分为多层边界层网格，可用于黏性计算。详尽的方法介绍见参考文献[13]、参考文献[14]。图3为生成的飞翼网格实例。

2.2 流场数值计算方法

流场计算在笛卡儿网格上基于格心格式的有限体积法对RAMS方程进行数值求解，湍流模型为Menter SST两方程模型[15]。对流项采用Roe格式[16]离散，交接面处的无黏通量计算时，使用最小二乘法重构获得单元内的梯度分布，獲得二阶空间精度，同时使用Venkatakrishnan限制器抑制间断附近的过冲和振荡。时间推进采用LU-SGS方法，可以有效提高CFL数，节省计算时间。采用本文气动计算方法获得的飞翼布局典型流场压力如图4所示。

2.3 优化方法

外形优化设计研究借助于课题组的飞行器外形优化设计平台，平台中集成了内含多种优化方法的优化工具包，优化时选取序列二次规划算法。作为基于梯度的经典数值型优化算法，序列二次规划法是一种求解约束优化问题常用的有效算法，计算效率高、可靠性好，通过将一般非线性约束优化问题转化为求解一系列的二次规划子问题，采用二次规划法逐步逼近原问题的解。

3 外形气动优化设计

3.1 优化设计模型

以FFD控制体包络的顶点位置为优化设计变量，以阻力C_D最小化为设计目标，限定升力C_L不低于给定的C_L0，要求典型翼截面最大厚度T_m不小于设定值T₀，选择工况H=0km、Ma=0.1、α=4°作为设计点，优化模型为：

X为优化设计变量组成的矢量，X_u、X_d为该矢量取值上、下边界。X包括控制体后掠角和控制顶点法向坐标参数，其中控制体后掠角是全局控制变量，使飞翼外形产生整体变化，控制顶点法向坐标主要改变外形的局部形状，优化飞翼翼型截面。

3.2 优化设计结果

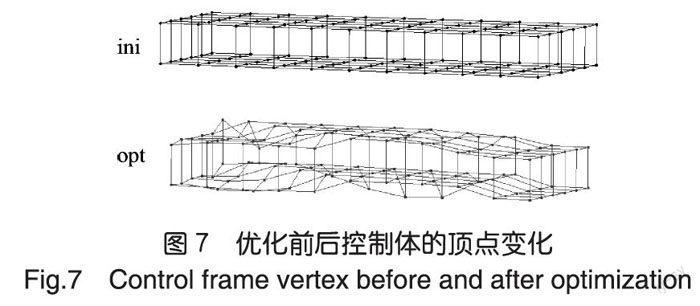
通过优化设计得到的飞翼无人机优化外形（opt）和初始基准外形（ini）平面，如图5所示，对应的FFD控制体平面和顶点变化如图6和图7所示。优化后控制体后掠角增大，使优化外形后掠角同步地增大。

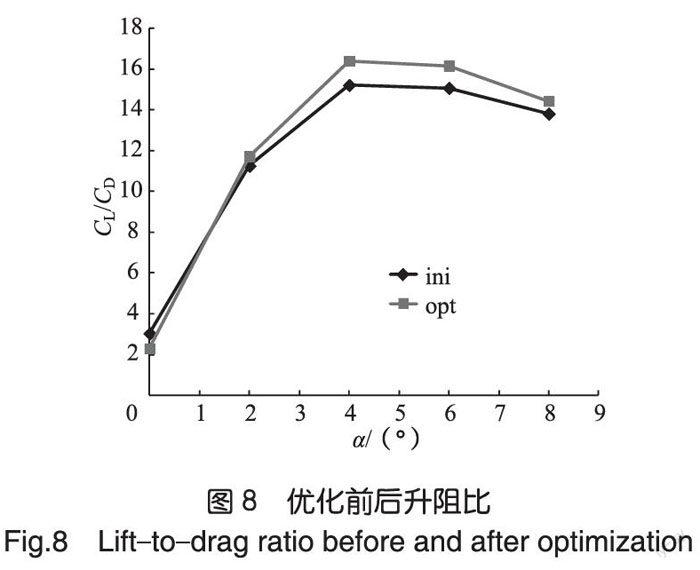
图8为优化前后设计马赫数下布局的升阻比随迎角变化曲线，相对初始基准外形ini，优化外形opt升阻比在设计点增加了7.9%，升阻比增加量部分由外形整体变化引起，其余来自截面形状变化。

4 结论

本文将FFD方法与网格重构方法相结合对飞翼无人机外形进行优化，得到以下结论：

（1）将FFD方法与网格重构方法相结合，外形参数化建模采用FFD变形技术，网格生成基于贴体笛卡儿自动网格重构技术，实现了对大尺度变化外形具有良好适应性的气动优化设计方法。

（2）对一种双后掠飞翼无人机布局外形完成了气动优化设计研究。通过优化设计使飞翼无人机的气动性能得到了有效提升，布局升阻比增加了7.9%。

（3）本文所建立的外形大位移，大变形气动优化设计方法，对其他复杂外形飞行器布局设计也是适用的。

参考文献

[1]Samareh J A.Survey of shape parameterization techniques forhigh-fidelity multidisciplinary shape optimization[J].AIAAJournal，2001，39（5）：877-884.

[2]朱心雄.自由曲线曲面造型技术[M].北京：科学出版社，2000.

[3]Kulfan B M，Bussoletti J E.“Fundamental”parametric geometryrepresentations for aircraft component shapes[R].AMA 2006-6948，2006.

[4]湛岚，余雄庆，沈琼.大型客机概念设计的外形参数化CAD模型[J].计算机工程与设计，2009，30（16）：3887-3890.

[5]王元元，张彬乾，陈真利.离散网格点FFD技术在飞行器优化设计中的应用[J].气体物理，2013，8（2）：45-50.

[6]徐家宽，白俊强，黄江涛，等.考虑螺旋桨滑流影响的机翼气动优化设计[J].航空学报，2014，35（11）：2910-2920.

[7]李彬，邓有奇，唐静，等.基于三维非结构混合网格的离散伴随优化方法明.航空学报，2014，35（3）：674-686.

[8]Lamousin H J，Waggenspack W N.NURBS-based free-formdeformations[J].Computer Graphics and Applicalions，1994，14（6）：59-65.

[9]孙家广.计算机图形学[M].北京：清华大学出版社，1998.

[10]王荣，闫溟，白鹏，等.飞翼无人机平面外形气动隐身优化设计研究[J].航空学报，2017，38（S1）：721532.

[11]鲍君波，王刚林，武哲.飞翼布局气动方案优选和试验验证[J].北京航空航天大学学报，2012，38（2）：180-184.

[12]Wang Z J，Kumar S.Complex dirty geometry handling with aninterior-to-boundary grid generation method[R].AIAA 2001-2538，2001.

[13]黄明惜，陈红全.用非结构直角网格和欧拉方程计算运载火箭绕流[J].宇航学报，2002，23（5）：66-71.

[14]刘周，周伟江.适于黏性计算的自适应笛卡儿网格生成及其应用[J].航空学报，2009，30（12）：2280-2287.

[15]Menter F R.Two equation eddy viscosity turbulence models forengineering applications[J].AIAA Journal，1994，32：1598-1605.

[16]Roe P.Approximate riemann solvers，parameter vectors，anddifference schemes[J].Journal of Computational Physics，1981，43：357-372.