关于带有协作/竞争机制时变积分器网络一致性的收敛速率

马麒超 秦家虎 李曼

摘要 本文探讨了时变无向网络达到状态一致过程中的收敛速率问题.首先基于一般的时变无向网络展开研究，证明了其收敛速率随耦合权重的增加而提高.同时，给出了收敛速率的明确下界，并指出这个下界是耦合权重的线性函数.基于这些结论，本文研究了带符号网络的收敛速率问题，发现只要带有正权值的边具有（δ，T）连通性，就可以增大这些边的权重而保持其余边（带有负权值）不變，使一致性以指数的速率达到.本文的证明过程主要基于完全一致可观这一概念.另外，本文也得到了这样的结论：一致性误差值可以从系统一段时间内的相对状态值中重建.这对于分布式网络中滤波器的状态估计有一定的借鉴意义.

关键词  时变（分布式）网络;指数收敛速率;带符号网络;完全一致可观

中图分类号  TP13

文献标志码  A

0 引言

近十几年来多智能体系统理论广受关注[1] .这是由于它能够描述自然界中广泛存在的有趣的生物群集现象，比如鸟类编队以及萤火虫同步闪光等.一般来说，多智能体系统是由多个智能体通过网络互联组成的，能够完成复杂任务的系统[1] .这些个体具有一定感知、测量、储存、计算、通信能力，并能够对周围环境做出反应.每个智能体通过与其相邻个体沟通来协调自己的目标与行为，最终完成一项复杂的任务.多智能体系统的一致性在多智能体系统的研究中占有重要的地位.所谓一致性是指随着时间的推移，多智能体系统中的所有智能体的状态或者输出达到相同的值.多智能体系统的其他行为模式，如聚集、编队、蜂拥、同步等[1-2] ，都是以一致性为基础的.

20世纪80年代，生态学家Reynolds提出了基于三条启发式规则的Boid模型，通过计算机仿真模拟自然界中鸟群、鱼群的群集行为.文献[3]则从统计力学的角度提出了一个离散时间模型，能够有效地描述简单个体之间相互影响导致的群集行为.Ren等[4] 指出，在切换网络情形下，有向通信拓扑具有联合连通的性质能够保证一致性的收敛.Moreau[5] 则进一步证明，在连续时变的系统中，对于上述联合连通的有向通信拓扑，一旦有 δ，T 连通性（如果在任意给定的时间窗口 T 内权重积分大于δ的边构成一个连通图，则称通信拓扑具有 δ，T 连通性），则能够保证一致性的指数收敛.文献[6]进一步确认了这一结论，并论证了在无向图中指数收敛速率对初值具有一致性.文献[7]探讨了如何弱化上述 δ，T 连通性的要求.Shi等[7] 得出，如果有向图的持续图连通，即如果仅保留在[0，∞）上积分值为无穷大的边仍能保持连通性，且不同边的权值之间满足一定的平衡关系，那么一致性能够以渐近的形式达到.文献[8]则给出了另一个有趣的结论，要求通信拓扑满足 δ i，T i 条件，即不要求存在一个固定的时间窗口T使得通信拓扑联合连通，而要求存在一列时间窗口使得联合连通成立.这里的T i随着i的增大可以趋近无穷大.在这个条件的基础上，文献[8]给出了使得时变无向图中积分器系统全局渐近收敛的充分必要条件.上述结论尽管非常优美，却忽略了对于收敛速率的刻画.

本文则进一步对时变无向图中实现状态一致的收敛速率进行了探讨，证明了在一般的时变无向图中，如果耦合权重增大，那么收敛速率也随之提高.同时，给出了收敛速率的明确下界，并指出这个下界是耦合权重的线性函数.基于这一结论，本文针对带符号的网络进行了探讨（即一个网络中边的权重可以为负数也可以为正数，这在社会网络的建模和分析中能够见到[9] ）.进一步，笔者发现只要带有正权值的边具有（δ，T）连通性，那么增大这些边的权重而保持其余边（带有负权值）不变，即可使一致性以指数的速率达到.本文的证明主要基于完全一致可观的概念.而且，在分析中可以得到一个额外但有意义的结论，即一致性误差值可以从系统过去一段时间的相对状态值中重建.这对于分布式网络中滤波器的状态估计有一定的借鉴意义.

1 图论相关概念

由N个节点组成的有向图可以用G= V，E 来表示，其中顶点集V={1，…，N}是有限的非空集合，边集EV×V是有序节点对组成的边的集合. i，j ∈E表示节点j能够获得节点i的信息，此时称i是j的邻居.记N i为节点i的邻居的集合.与有向图不同，无向图中的 i，j 表示节点i和节点j能互相获取对方的信息.

所以定理1，2在耦合强度足够大的时候仍然成立.证明结束.

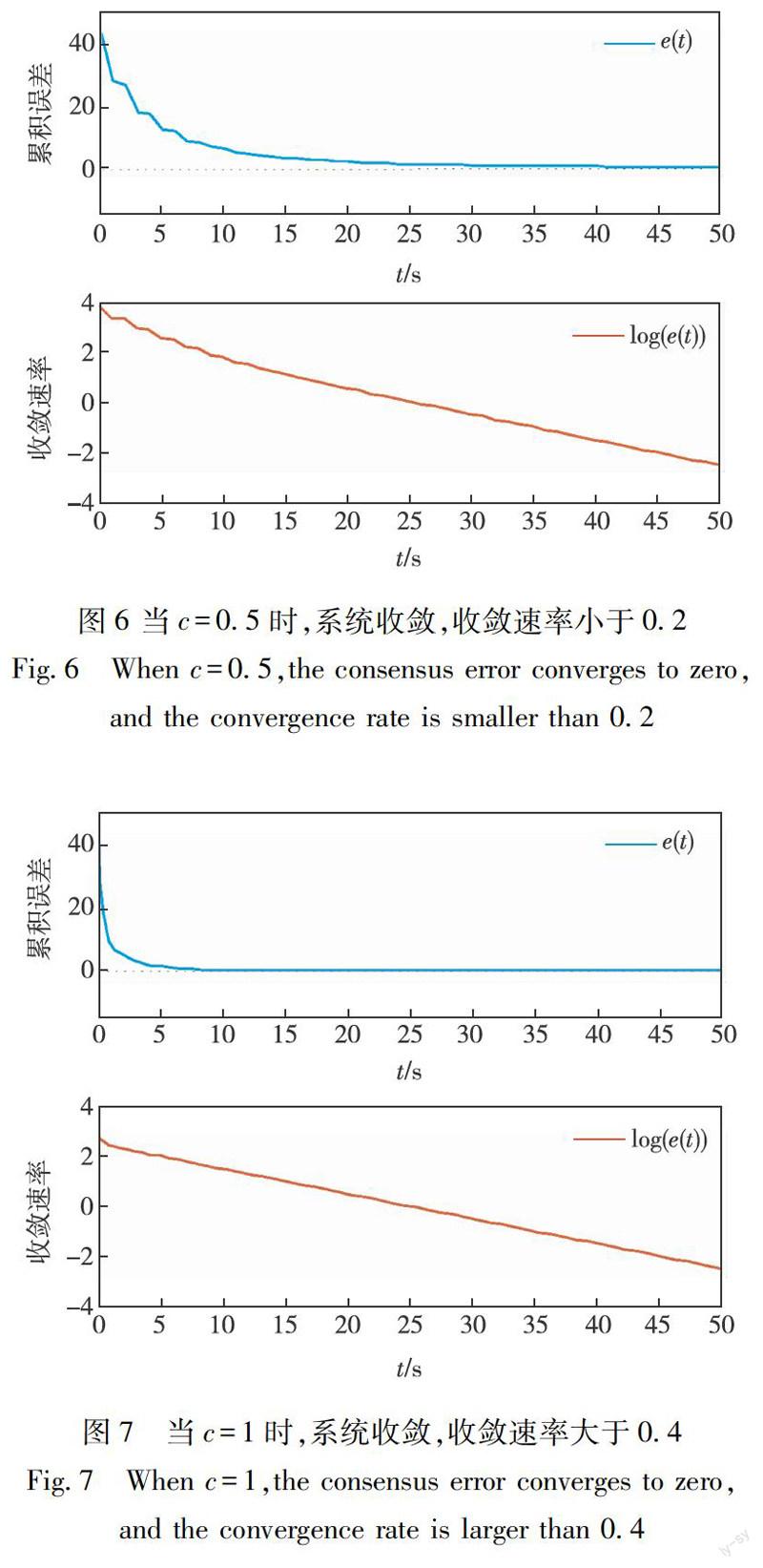
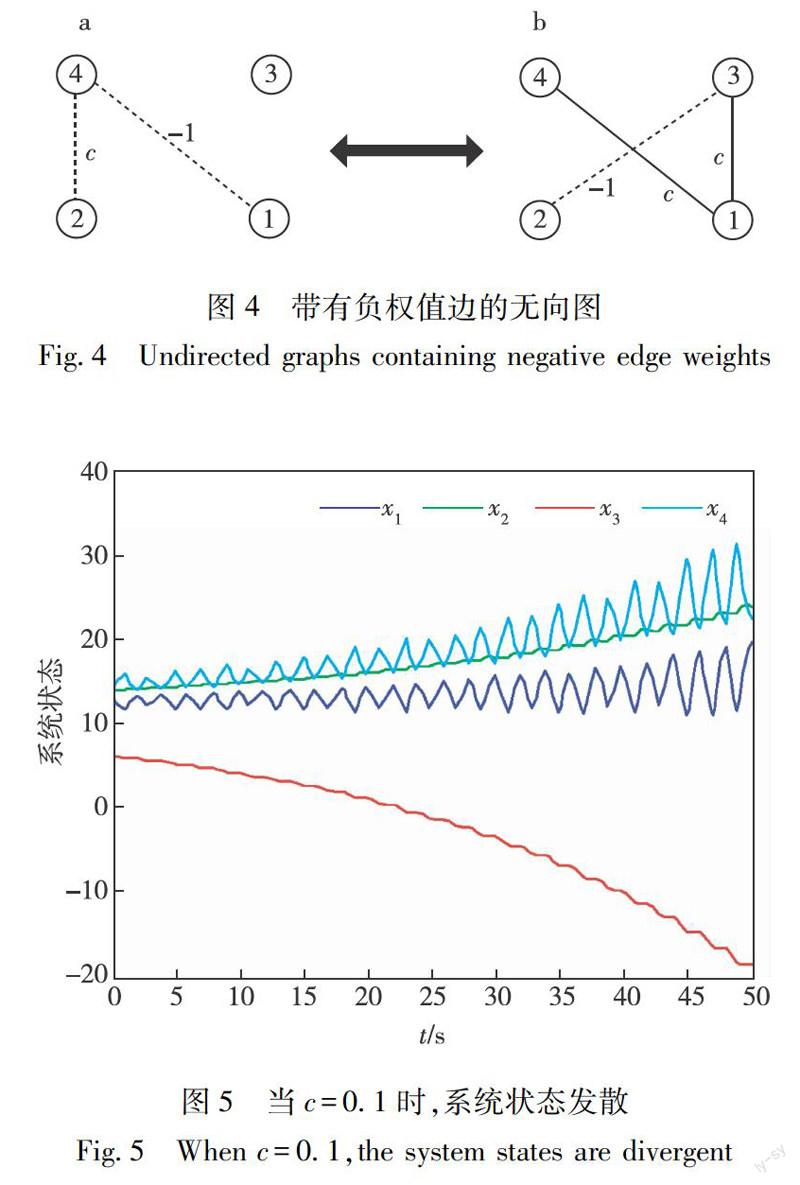
例2   考虑图4所示的G  a ，G  b .它们都是无向图，并且它们的并所得的图中正权值的边构成连通图，即G  a ∪G  b 包含一个有正权值的边构成的生成树.在仿真验证中，我们让通信拓扑在G  a ，G  b 之间以周期1  s  来回切换.系统的初值由随机程序生成.G  a ，G  b 中边的权重设置为c>0. 图5表明当c=0.1，由于负边的存在，系统并不收敛.当c增大到0.5时可以看到系统开始收敛，并以指数速率收敛，其速率小于0.2 （图6）.当c=1即耦合强度增大时，可以看到收敛速率增加，并且大于0.4 （图7）.这同样验证了本文的结论，耦合强度的增大能够提升收敛的速率，同时抑制负边带来的影响使得系统达到一致.

7 总结

本文进一步对时变无向网络中的收敛速率进行了探讨.我们证明了，在一般的时变无向网络中，如果耦合权重增大那么收敛速率也随之提高.我们给出了收敛速率的明确下界，这个下界是耦合权重的线性函数.在此基础上，针对带符号网络进行了探讨，发现只要带有正权值的边具有（δ，T）连通性，那么增大这些边的权重而保持其余边（带有负权值）不变，一致性就能以指数的速率达到.整个证明过程使用了完全一致可观的概念.基于此还可以得到这样的结论，即一致性误差值可以从系统过去一段时间的相对状态值中重建.

參考文献

References

[ 1 ]

Qin  J，Ma Q，Shi Y，et al.Recent advances in consensus of multi-agent systems：a brief survey[J].IEEE Transactions on Industrial Electronics，2017，64（6）：4972-4983

[ 2 ] Cao  M，Morse A S，Anderson B D O.Reaching a consensus in a dynamically changing environment：convergence rates，measurement delays，and asynchronous events [J].Siam Journal on Control & Optimization，2008，47（2）：601-623

[ 3 ] Altafini C.Consensus problems on networks with antagonistic interactions[J].IEEE Transactions on Automatic Control，2013，58（4）：935-946

[ 4 ] Ren  W，Beard R W.Consensus seeking in multiagent systems under dynamically changing interaction topologies[J].IEEE Transactions on Automatic Control，2005，50（5）：655-661

[ 5 ] Moreau  L.Stability of continuous-time distributed consensus algorithms[C]∥

2014 43rd IEEE Conference on Decision and Control（CDC），2004：3998-4003

[ 6 ] Anderson  B D O，Shi G，Trumpf J.Convergence and state reconstruction of time-varying multi-agent systems from complete observability theory[J].IEEE Trans Autom Control，2017，62（5）： 2519-2523

[ 7 ] Shi G，Johansson K H.The role of persistent graphs in the agreement seeking of social networks[J].IEEE Journal on Selected Areas in Communications，2013，31（9）：595-606

[ 8 ] Ortega  R，Barabanov N.Global consensus of time-varying multi-agent systems without persistent excitation assumptions[J].IEEE Transactions on Automatic Control，2018，DOI： 10.1109/TAC.2018.2803114

[ 9 ] Shi  G，Altafini C，Baras J S.Dynamics over signed networks[J].e-Print，2017，arXiv：1706.03362

[10] Anderson  B D O，Moore J B.Detectability and stabilizability of time-varying discrete-time linear systems[J].Siam Journal on Control & Optimization，1981，19（1）：20-32

[11] Anderson  B.Exponential stability of linear equations arising in adaptive identification[J].IEEE Trans Auto Control，1977，22（1）：83-88

[12] Antonio Lorí，Panteley E.Uniform exponential stability of linear time-varying systems：revisited[J].Systems & Control Letters，2002，47（1）：13-24

[13] Horn R A，Johnson C R.Matrix analysis[M].Cambridge：Cambridge University Press，1985

On convergence speed of interacting integrators over

cooperative and competitive undirected networks

MA Qichao 1 QIN Jiahu 1 LI Man 1

1 Department of Automation，University of Science and Technology of China，Hefei 230027

Abstract  The convergence speed in the distributed consensus of integrators over both cooperative and competitive undirected networks is investigated in this paper.It has been well known that as long as the （δ，T） connectivity condition is satisfied，exponential convergence of the consensus can be attained.We further show that，for a cooperative network，increasing the coupling strength can improve the convergence speed.The lower bound of the convergence is also explicitly specified with respect to the coupling strength.Based on this，in the competitive network，the convergence of consensus can be guaranteed by strong cooperative couplings dominating the competitive ones.The results of this paper are established by means of a uniformly completely observable theory.We also show that it is possible to reconstruct the consensus error at a certain time instant from the observations of the past relative state information over  a fixed length interval.

Key words  time-varying network;convergence speed;signed networks;uniformly completely observable