基于改进布谷鸟搜索算法的种子园空间布局优化
王 路 漫, 王 建 新
( 1.北京林业大学 信息学院, 北京 100083;2.北京大学 医学部 医用理学系, 北京 100191 )
0 引 言
林木育种作为林业生产活动中重要的组成部分,是提升我国林业生产经济效益的基础和重要手段.目前,在我国多个地区,纷纷建立了以林木种子园为主要形式的育种基地.林木种子园是由经过筛选的优良家系按营建设计要求,以生产优良品质林木种子为目的建立的特种人工林[1-3].从现代林木育种经营考虑,种子园不仅是良种繁殖基地,直接为生产提供大量优质种子,同时随着生物信息技术的发展,种子园也成为生产改良种子的重要途径,更好地在育种与育林之间搭建桥梁,从而通过提高种子的遗传品质来直接影响未来林分的质量.
为了在种子园营建过程中产生优良遗传品质的种子,使种子园培育出的树种更好地适应外界环境变化,抵御突然出现的病虫害、干旱等恶劣情况,最重要的是在种子园营建过程中提高种子园子代的遗传多样性水平,目前主要面临的问题是在待栽种亲本的数量和种类固定的前提下,以降低树种之间的近交率,提高种子园的多样性水平为目的,设计种子园优化栽培种植(以下简称栽植)方案.为了便于实施,目前最常用的种子园栽植方案为随机排列布局.该方案有利于树木间的充分杂交,同时适应复杂地形,简单易行[4-5].除了随机配置方法以外,王昊提出了一种区组设计方法,每个区组尽可能包含所有的亲本,使区组内属于同一亲本的植株尽可能保持最大的距离[6].程祥等也采用更为详细的区组设计方法,即同一区组内相同家系单株之间顺序错位排布,以达到提高异交率、降低近交率或自交率的目的[7].针对不同育种条件、树种家系,很多对种子园配置的研究是在随机排列方式或区组设计方法的基础上进行改进的[8-10].但上述所有方法都是从局部考虑优化策略,并未从整体和全局考虑,不能量化栽植时亲本间近亲交配对子代的影响,也不能根据所有栽种树种的基因型来精准地制定最优化栽植方案.
在种子园营建过程中必须考虑亲本间的亲缘关系,才能将近交率最小化,确保种子园种子产量和品质的稳固提高,使树种改良项目得到长远发展.但传统的种子园多采用随机自由授粉方式,其获得的子代虽然包含所有可能的杂交组合,但从中选出的优良单株可能存在近亲关系[11].在不了解种批的遗传基础和遗传多样性背景的情况下,在造林过程中大量引入遗传基础狭窄的树种,同样存在遗传单一性的危险.随着高通量测序技术的快速发展,通过对林木树种进行基因测序,可精确地得到树种的基因序列,进而在DNA分子水平上对种子园各家系的遗传品质做出正确的评价.同时,在种子园配置过程中,可以综合考虑影响树木重要性状如生长量、材性以及抗逆性等基因位点的遗传结构和遗传多样性状况,对进一步提高种子园的产量和质量具有非常重要的意义[12].
因此,为了提升种子园的栽种品质,根据待栽种植株数量及针对优良性状相关位点的基因型数据,需要获得种子园空间布局的最优化方案.但当种子园的栽种规模增大时,结合多个与优良性状相关基因位点的种子园设计是一个NP-难问题,该类问题不能使用传统的如穷举法、动态规划等方法解决,而需要使用智能优化算法进行求解.但针对上述种子园空间布局的问题,目前并未发现使用智能优化算法进行相关研究.因此,本文提出采用布谷鸟搜索算法对种子园空间布局进行最优化配置.为了验证该算法的可行性和有效性,随机产生不同规模的种子园栽种树木的模拟数据,使用布谷鸟搜索算法和遗传算法对模拟数据进行最优化求解,并对两种算法的性能和计算结果进行比较,提高种子园子代的遗传多样性,从而为种子园育种提供精准的理论依据.
1 种子园栽植方案设计的问题
本文需要解决的问题是在已知亲本数量和基因型的前提下,设计种子园的栽植方案使种子园树木子代具有最大的遗传多样性.为了更好地解决这个问题,首先需要将实际问题进行抽象描述.
1.1 种子园相关数据输入
在进行种子园空间布局最优化方案求解之前需要获取种子园的相关数据作为模型的输入,其中包括:种子园待栽种植株的位置编号、栽种位置之间的空间距离、决定植株优良性状的关键位点以及每个位点的基因型4方面的数据.
(1)栽种位置编号:为计算简便,忽略种子园的地形地貌特征及风向、种间花粉污染等因素,假设种子园为规则地块,需要栽种m行n列棵树木,其空间布局如图1所示.所有树木均匀排布,每个位置对应的坐标为(i,j),其中1≤i≤m,1≤j≤n.

●●●●●●●●●●(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)(1,7)(1,8)(1,9)(1,10)●●●●●●●●●●(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)(2,7)(2,8)(2,9)(2,10)●●●●●●●●●●(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)(3,7)(3,8)(3,9)(3,10)●●●●■●●●●●(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)(4,7)(4,8)(4,9)(4,10)●●●●●●●●●●(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)(5,7)(5,8)(5,9)(5,10)●●●●●●●●●●(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)(6,7)(6,8)(6,9)(6,10)●●●●●●●●●●(7,1)(7,2)(7,3)(7,4)(7,5)(7,6)(7,7)(7,8)(7,9)(7,10) ︙●●●●●●●●●●(m,1)(m,2)(m,3)(m,4)(m,5)(m,6)(m,7)(m,8)(m,9)(m,10) … ●(1,n)●(2,n)●(3,n)●(4,n)●(5,n)●(6,n)●(7,n)︙●(m,n)
图1 种子园空间栽种布局示意图
Fig.1 Sketch map of spatial cultivation layout of seed orchard
为了方便该问题求解,也可以将种子园中的栽种位置采用以下方式进行编号,即
D(i,j)=(i-1)n+j; 1≤i≤m,1≤j≤n
(1)
因此,栽种位置可以转化为如下矩阵:
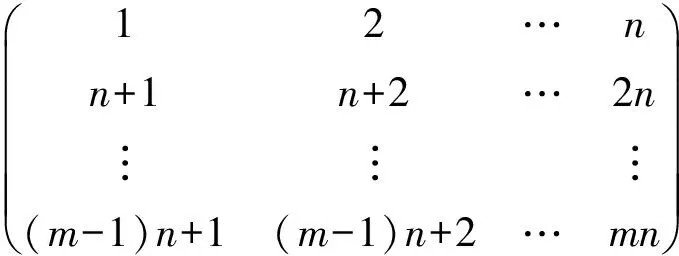
(2)栽种位置之间的空间距离:
{dl,k};l,k=1,2,…,mn
其中l、k为种子园栽种位置的编号.
(3)种子园中mn个位置需要栽种植株的编号为
{tk};k=1,2,…,mn
初始待栽种植株的编号为1,2,…,n,n+1,n+2,…,2n,…,(m-1)n+1,(m-1)n+2,…,mn,对应mn个栽种位置,求解的种子园栽植布局最优方案X*={tk},tk为种子园中第k个位置栽种植株的编号,即最优解是植株编号的序列.
(4)决定植株优良性状的p个关键位点为
{gp};p=1,2,…,P
可以通过已有成熟的技术获取这些位点.当最终的性状在数值上有较大差异时,可以采用QTL技术发现这些位点;如果最终的性状相同或差异不大,可以采用功能作图(functional mapping)方法[13]或者E-index方法[14-16]发现关键位点.
(5)针对上述关键位点,每个植株都具有相应的基因型
{qtk,p};k=1,2,…,mn,p=1,2,…,P
由于每个关键位点有3种可能的基因型,即AA、Aa和aa,而每一个个体在固定的位点上必居其一,qtk,p可以取但只能取3个值0、1、2中的一个,分别对应AA、Aa和aa这3种基因型.
1.2 目标函数
营建种子园的最终目标是得到配置方案中所有亲本在其邻域范围内的亲缘差异性之和的最大值,为了强化主要影响因素,本文所指某亲本的邻域范围为与该亲本距离小于某一给定值d的植株.例如根据图1所示,如果目标植株个体是(4,5),为了强化主要影响因素,只关心在所画半径d范围内的植株个体与目标个体的多样性差异,即要考虑与目标个体相邻的20个植株.因此在式(2)中,只考虑与目标植株tk距离小于等于d的植株,将上述问题的目标函数转化为求解所有植株间多样性差异之和的最大值,其公式表示如下:
(2)
式中:F为每种种子园栽植方案即解{tk}对应的目标函数.f(tk)为与目标植株相邻半径小于等于d的所有植株的基因型差异性之和.dtl,tk为植株tl与tk之间的栽种距离.若两棵树在第p个关键位点的基因型不同,即qtl,p≠qtk,p时,Q(qtl,p,qtk,p)=1;若两棵树在第p个关键位点的基因型相同,即qtl,p=qtk,p时,Q(qtl,p,qtk,p)=0.
2 改进的布谷鸟搜索算法
布谷鸟搜索算法是Yang等通过研究布谷鸟寻找鸟窝放置鸟蛋的行为以及结合一些鸟类飞行行为提出的最优化算法[17-18].在解决许多最优化问题时,通过利用一些标准测试函数和随机测试函数进行大范围的对比实验,发现布谷鸟搜索算法在求最优解方面比其他启发式算法更胜一筹[19-20].同时由于该算法具有简单易行并且在解决特殊问题时无须重新匹配大量参数等优点,其可以用来求解很多领域的问题.因此本文采用布谷鸟搜索算法对种子园空间布局进行最优化求解.但布谷鸟搜索算法最初是为解决连续优化问题而提出的,而种子园空间布局优化问题的解是离散值[21],因此在本文中需要对布谷鸟搜索算法进行改进,使它适用于求解种子园空间布局的优化方案.改进算法的具体实现步骤如下:
步骤1针对种子园假设的前提条件及要解决的最优化问题,随机产生u个初始化解{Xr},r=1,2,…,u,其中每个解都是种子园mn个位置需要栽种的植株编号序列,即u种种子园植株空间布局栽种方案.
步骤2按照式(2)对u个初始化解进行目标函数F的计算,其中对应目标函数值最大的解为当前最优解X*.
步骤3将当前的u个解记作{Xr},按照式(3)计算出u个新的解{X′r},产生的新解可能是潜在的更好的解.
X′r=Xr+Sl(Xr-X*)
(3)
其中Sl是服从Lèvy分布的随机数;X*是当前的最优解.
步骤4对计算产生的解X′r进行离散化转换成关于种子园栽植方案实际问题的解X″r,r=1,2,…,u,该转换过程如下:
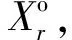

表1 布谷鸟搜索算法计算解的过程
将运行的迭代次数记为N=N+u,按照式(2)对每个解X″r进行目标函数的计算,并与上一组解Xr的目标函数进行比较,得到对应目标函数值最大的最优解X*.
步骤5为了避免算法陷入局部最优,提高找到全局最优解的能力,在当前所有解中按照以下方式剔除某一部分不好的解,产生新解.具体操作过程如下:
产生服从均匀分布的随机数v1∈(0,1),并与初始设定的替换解概率pa=0.25进行比较,若v1>pa,则按照式(4)对当前解进行改变,反之不变.如果需要改变当前解,则要按照步骤4中的方法把式(4)中产生的解Xr转换为X′r,同时再次计算目标函数(2),并与上一组解对应的目标函数进行比较,选出最优解X*,并将迭代次数记为N=N+u.
X′r=Xr+v2(X1-X2)
(4)
其中X′r是新解,Xr是之前的解,v2是(0,1)区间均匀分布的随机数,X1和X2是从当前解中随机挑选出来的两个解.
步骤6判断迭代是否满足终止条件,即N>Nmax,其中Nmax是事先设定好的最大迭代次数.若满足该终止条件,则最优解Xo=X*,若不满足该条件,则重复步骤3~5.
3 实验结果与分析
为了验证布谷鸟搜索算法的性能,首先按如下前提假设生成种子园亲本树木的模拟数据:
(1)树木与性状相关的基因位点6个,每个基因位点可能存在3种基因型(AA、Aa、aa).
(2)树木亲本的邻域范围d=3,即考虑与目标树木个体距离小于等于3的所有树木个体的基因型差异.
然后使用Matlab编程实现布谷鸟搜索算法对这些数据的最优化求解,得到种子园中树木之间基因型差异性最大的栽植方案.最后通过以下方式调整该算法的参数,产生不同的最优化计算结果,并对结果进行对比分析.其中算法迭代次数为算法运行过程中计算目标函数的次数.
(1)设置不同种子园规模
针对种植树木数量不同的模拟数据进行求解,设置算法的迭代次数均为4 000,计算其目标函数,得到如图2所示结果.从结果中可以看出,随着种子园种植树木数量的增加,亲缘多样性明显增大.因此为了提高树木的遗传多样性,需要扩大种子园的规模.

图2 布谷鸟搜索算法求解不同规模的种子园空间布局
Fig.2 The different scale seed orchard spatial layout calculated by cuckoo searching algorithm
(2)设置不同算法迭代次数
设置种子园栽种树木均为100棵,并将其规则地种于10×10的种子园中,设置不同算法迭代次数,得到如图3所示的结果.即对于相同的模拟数据,总体来说,随着迭代次数增多,遗传多样性有提高的趋势,但提高的幅度不大.这说明改进的布谷鸟搜索算法通过较少迭代次数就可以得到较优的结果.

图3 比较不同迭代次数的布谷鸟搜索算法结果Fig.3 Comparison of performance with different iterations by cuckoo searching algorithm
(3)不同模拟数据
针对随机产生的6组模拟数据设置相同的参数,即设置算法的迭代次数均为4 000,种子园栽种树木均为100棵,进行最优化求解得到如图4所示的结果.从该结果中可以看出,对于不同的模拟数据,存在较大的遗传多样性差异.

图4 比较不同数据集的布谷鸟搜索算法求解结果
Fig.4 Comparison of performance with different data sets by cuckoo searching algorithm
为了进一步验证改进的布谷鸟搜索算法的有效性,使用布谷鸟搜索算法以及遗传算法[22]对相同的模拟数据(栽种棵数k=100,将其规则地种于10×10的种子园中;树木与性状相关的基因位点6个;树木亲本的邻域范围d=3)进行最优化求解,求出使种子园中树木之间基因型差异性最大的栽植方案.其中算法运行过程中计算目标函数总次数作为算法迭代总次数,设置遗传算法的交叉概率pc=0.600,变异概率pm=0.001.得到两种算法运行的结果如图5所示.在迭代次数相同的情况下,布谷鸟搜索算法得到的目标函数值都高于遗传算法所得到的值,即对于相同的模拟数据,使用布谷鸟搜索算法计算得到的植株空间布局栽植方案使其子代具有更大的多样性.因此布谷鸟搜索算法优于遗传算法,在求解种子园空间布局优化方面具有更强的优势.
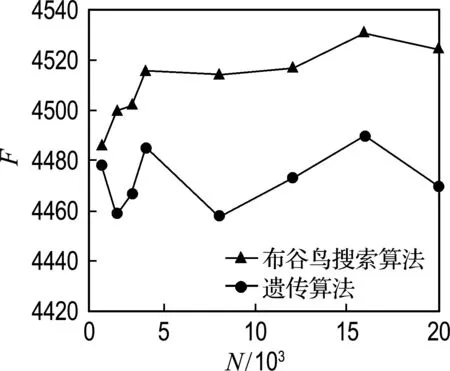
图5 布谷鸟搜索算法与遗传算法的比较Fig.5 Comparison of performance between cuckoo searching algorithm and genetic algorithm
4 结 语
本文针对种子园空间布局的优化问题,创新性地使用改进的布谷鸟搜索算法进行求解,通过设置不同的方式,对该算法性能进行评估,最后针对相同的模拟数据,将布谷鸟搜索算法与遗传算法进行比较,结果对于所设定的不同运行迭代次数,改进的布谷鸟搜索算法均有较快的收敛速度和较高的求解精度,并且算法性能上占优.因此针对种子园空间布局优化问题,可以采用本文改进的布谷鸟搜索算法很好地求解,同时该算法还可以从以下3个方面进行进一步扩展:
(1)本文采用的改进布谷鸟搜索算法可以扩展到任何树种的种子园空间布局优化问题,其中亲本数量和基因型数据可以为真实种子园植株数据.
(2)该算法可以用于不规则地块或不等距栽种树木的非均匀排布的种子园配置问题.
(3)该算法也可以有效地运用到与任意优良性状如树高、胸径等相关的基因位点,只要可以获得相应植株的基因型数据,就可以采用本文的布谷鸟搜索算法有效地进行求解.
[1] 杨培华,樊军锋,刘永红,等. 油松高世代种子园营建技术[J]. 中南林学院学报, 2005,25(6):65-69.
YANG Peihua, FAN Junfeng, LIU Yonghong,etal. Studies on establishing techniques for the advanced generation seed orchards ofPinustabulaeformisCarr [J].JournalofCentralSouthForestryUniversity, 2005,25(6):65-69. (in Chinese)
[2] 王章荣. 林木高世代育种原理及其在我国的应用[J]. 林业科技开发, 2012,26(1):1-5.
WANG Zhangrong. The principle of high generation tree breeding and its application in China [J].ChinaForestryScienceandTechnology, 2012,26(1):1-5. (in Chinese)
[3] 苏顺德,肖 晖,林文龙,等. 马尾松第2代种子园营建关键技术[J]. 福建林业科技, 2013,40(4):45-50, 104.
SU Shunde, XIAO Hui, LIN Wenlong,etal. Key techniques of establishment of the 2nd-generation seed orchard ofPinusmassoniana[J].JournalofFujianForestryScienceandTechnology, 2013,40(4):45-50, 104. (in Chinese)
[4] 屈柏林,周长虹,蔡胜国,等. 华北落叶松二代种子园营建技术研究[J]. 河北林果研究, 2015,30(1):41-44.
QU Bailin, ZHOU Changhong, CAI Shengguo,etal. Establishment technique of second-generation seed orchards forLarixprincipis-rupprechtii[J].HebeiJournalofForestryandOrchardResearch, 2015,30(1):41-44. (in Chinese)
[5] 楚永兴,张荣贵,陈有祥,等. 屏边县秃杉无性系种子园营建技术[J]. 林业调查规划, 2017,42(1):106-110,142.
CHU Yongxing, ZHANG Ronggui, CHEN Youxiang,etal. Construction technology of clonal seed orchard of Taiwania flousiana county [J].ForestInventoryandPlanning, 2017,42(1):106-110,142. (in Chinese)
[6] 王 昊. 林木种子园研究现状与发展趋势[J]. 世界林业研究, 2013,26(4):32-37.
WANG Hao. Research progress and development trend of tree seed orchard [J].WorldForestryResearch, 2013,26(4):32-37. (in Chinese)
[7] 程 祥,张 梅,毛建丰,等. 有限种群油松种子园的遗传多样性与交配系统[J]. 北京林业大学学报, 2016,38(9):8-15.
CHENG Xiang, ZHANG Mei, MAO Jianfeng,etal. Gene diversity and mating system ofPinustabuliformisin finite population seed orchard [J].JournalofBeijingForestryUniversity, 2016,38(9):8-15. (in Chinese)
[8] 王 颖,刘克俭,王 江,等. 长白落叶松1.5代种子园营建技术[J]. 吉林林业科技, 2016,45(5):4-6.
WANG Ying, LIU Kejian, WANG Jiang,etal. The construction technology ofLarixolgensis1.5 generation seed orchard [J].JournalofJilinForestryScienceandTechnology, 2016,45(5):4-6. (in Chinese)
[9] 赵艳妮,赵东战. 油松无性系种子园营建技术[J]. 陕西林业科技, 2012(2):92-94.
ZHAO Yanni, ZHAO Dongzhan. The technique on establish ofPinustabulaeformisclone seed orchard [J].ShaanxiForestScienceandTechnology, 2012(2):92-94. (in Chinese)
[10] 袁虎威,梁胜发,符学军,等. 山西油松第二代种子园亲本选择与配置设计[J]. 北京林业大学学报, 2016,38(3):47-54.
YUAN Huwei, LIANG Shengfa, FU Xuejun,etal. Parental selection and deployment design in the second-generation seed orchard of Chinese Pine in Shanxi Province [J].JournalofBeijingForestryUniversity, 2016,38(3):47-54. (in Chinese)
[11] 张 薇,龚 佳,季孔庶. 马尾松实生种子园遗传多样性分析[J]. 分子植物育种, 2008,6(4):717-723.
ZHANG Wei, GONG Jia, JI Kongshu. Genetic diversity for seedling orchard of Masson′s Pine [J].MolecularPlantBreeding, 2008,6(4):717-723. (in Chinese)
[12] 龚 佳. 马尾松实生种子园遗传多样性研究 [D]. 南京:南京林业大学, 2007.
GONG Jia. Genetic diversity of microsatellites (SSRs) for seedling seed orchard of Masson′s Pine (PinusmassonianaL.) [D]. Nanjing: Nanjing Forestry University, 2007. (in Chinese)
[13] WU R, LIN M. Functional mapping-how to map and study the genetic architecture of dynamic complex traits [J].NatureReviewsGenetics, 2006,7(3):229-37.
[14] QI Jiandong, SUN Jianfeng, WANG Jianxin. E-index for differentiating complex dynamic traits [J].BioMedResearchInternational, 2016,2016:1-13.
[15] 孙鉴锋,王建新. 一种基于E-index方法区分复杂性状的分析工具[J]. 中国生物工程杂志, 2017,37(2):93-100.
SUN Jianfeng, WANG Jianxin. An analysis tool based on E-index method for differentiating complex traits [J].ChinaBiotechnology, 2017,37(2):93-100. (in Chinese)
[16] 邬荣领,王建新. 一种基于基因互作的植物生长预测调控方法及系统: 201410077450.0 [P]. 2014-05-21.
WU Rongling, WANG Jianxin. A predicting method and system for plant growth based on gene interaction: 201410077450.0 [P]. 2014-05-21. (in Chinese)
[17] YANG X S, DEB S. Cuckoo search via Lévy flights [C] //2009WorldCongressonNatureandBiologicallyInspiredComputing,NABIC2009-Proceedings. Coimbatore: IEEE Computer Society, 2009:210-214.
[18] YANG X S. Cuckoo search for inverse problems and simulated-driven shape optimization [J].JournalofComputationalMethodsinSciencesandEngineering, 2012,12(1/2):129-137.
[19] WANG Hui, WANG Wenjun, SUN Hui,etal. A new cuckoo search algorithm with hybrid strategies for flow shop scheduling problems [J].SoftComputing, 2017,21(15):4297-4307.
[20] 宋玉坚,叶春明,黄佐钘. 多资源均衡优化的布谷鸟算法[J]. 计算机应用, 2014,34(1):189-193.
SONG Yujian, YE Chunming, HUANG Zuoxing. Cuckoo search algorithm for multi-resource leveling optimization [J].JournalofComputerApplications, 2014,34(1):189-193. (in Chinese)
[21] BENSEDIRA B, LAYEB A, HABBAS Z. Discrete cuckoo search applied to capacitated arc routing problem [J].InternationalJournalofMetaheuristics, 2017,6(1/2):37-54.
[22] HOLLAND J H.AdoptioninNaturalandArtificialSystem[M]. Ann Arbor: University of Michigan Press, 1975:32-48.

