基于模糊GO法的惯性导航系统可靠性研究

王 海 朋， 段 富 海*， 江 秀 红

( 1.大连理工大学 机械工程学院, 辽宁 大连 116024；2.沈阳航空航天大学 电子信息工程学院， 辽宁 沈阳 110136 )

0 引 言

在国防高可靠性领域，武器装备的可靠性一直受到高度重视．平台惯性导航系统(inertial navigation system，INS)是复杂高可靠性机电一体化系统．近年来由于INS数据错误和功能失效而引起的事故时常发生，因此对作为运载体主信号源的INS可靠性评价尤为重要．INS可靠性分析主要存在的问题是[1]：①装在飞机、导弹、通信卫星等运载体上的INS是典型小子样系统，其可靠性试验周期长且代价昂贵，现场试验数据少，很难获取元件精确的失效数据；②INS可靠性存在一定的不确定性，如故障发生机理和故障模式复杂多变，部件和分系统对系统可靠性影响不确定等；③传统可靠性模型缺乏自适应修正能力．因此急需寻求一种有效的不确定性INS的可靠性分析方法．

GO法(goal-oriented methodology)是一种有效的复杂系统可靠性分析方法[2]，特别适合有电流、气流、液流等实际物流产生的多状态复杂系统可靠性分析[3]．如樊冬明等[4]建立了基于动态贝叶斯网络的可修GO法模型，并通过核电站高压注水系统验证了所提模型的有效性；江秀红等[5]提出了一种基于GO法的INS预测维修平台设计方法；陈洁等[6]提出了贝叶斯GO法，并对深水关井作业进行了可靠性分析．传统GO法的系统可靠性分析假设元件存在2种或3种状态，其状态概率值精确可知．因此传统GO法用精确值描述元件的各状态概率，不能反映出真实情况，会降低系统可靠性分析结果的可信度．

模糊可靠性理论是处理可靠性工程中不精确和不确定性问题的一种新方法[7]，利用模糊数学在处理不确定性信息方面的优势，使复杂系统可靠性和安全性评估结果更真实可信．如文献[8-9]将零部件的失效概率模糊化，提出了一种基于模糊理论的故障树算法，并应用到工程系统的可靠性评估中；文献[10-11]将事件发生的成功概率用三角模糊数表示，提出了基于三角模糊数的GO法，但均不适用于评估多状态元件和系统的可靠性．文献[12]将工程变量处理为随机变量和模糊变量，提出了一种可综合处理模糊不确定信息和随机不确定信息的可靠度计算模型；文献[13]将具有危害性事件发生的可能性和严重程度模糊化，提出了一种基于模糊理论的风险评估方法．

针对传统GO法的不足，本文引入三角模糊数和扩展原理分别对输入、输出数据的模糊不确定性进行量化，提出一种模糊数学理论与GO可靠性模型相结合的多状态系统可靠性分析方法——模糊GO法，并将其应用到INS可靠性研究中．

1 数据的模糊算法

1.1 模糊集合的截集

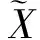
1.2 数据的三角模糊数转化方法

三角模糊数是最常见的模糊数之一，具有计算简单、表达直观等优点，广泛用于解决可靠性领域中模糊不确定性问题[14-15]．为描述某事件发生的模糊不确定性，将某事件发生概率的精确值处理为可进行模糊化运算的三角模糊数，用式(1)方法进行模糊化处理，构造三角模糊数(l,m,h)：

l=p·(1-Ef),m=p,h=p·(1+Ef)

(1)

式中：l、m、h分别为事件发生的最小可能值、最可能值、最大可能值；p为事件发生的概率；Ef为误差因子，可根据实际工况和领域专家经验选取．

1.3 扩展原理和参数规划

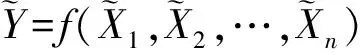
(2)

(3)

下边界：

(4a)

上边界：

(4b)

2 基于模糊GO法的可靠性分析原理

GO法是一种以成功为导向的图形化系统可靠性分析方法[18]．模糊GO法是将模糊集合理论与GO可靠性模型相结合，引入三角模糊数和扩展原理对输入、输出数据的模糊不确定性进行量化，其可靠性分析原理如图1所示，步骤如下：

(1)分析系统的基本原理，明确各元件、子系统的逻辑结构；

(2)根据单元功能和单元输入、输出信号之间的逻辑关系确定对应单元的操作符类型[2]；

(3)根据系统物流逻辑上的进程，用信号流连接各操作符，生成GO图；

(4)从输入操作符开始，按照各操作符的运算规则，沿着信号流，得到系统的输出状态及状态概率表达式；

(5)采用式(1)的处理方法，将元件各状态发生概率的精确值转化为三角模糊数，得到元件各状态的模糊可靠性数据；

(6)用扩展原理将系统的输出状态概率表示为一个新的模糊数，按步骤(5)得到的三角模糊数作为扩展原理的输入变量，按步骤(4)得到的状态概率表达式作为扩展原理的模糊映射关系，用参数规划方法得到直观的系统模糊状态概率隶属度函数，据此对系统做出可靠性分析与评价．

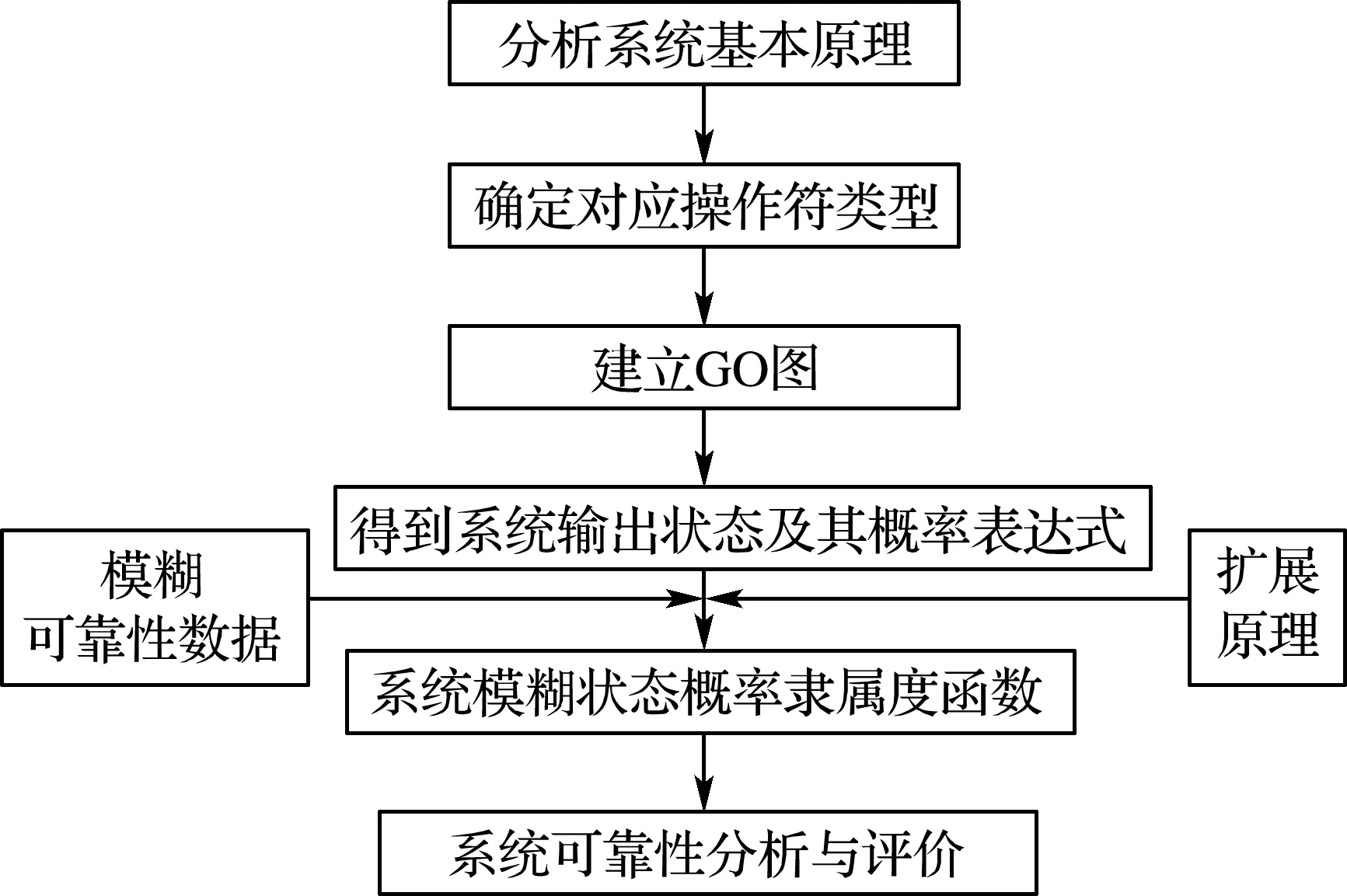
图1 模糊GO法可靠性分析原理Fig.1 Reliability analysis principle of fuzzy GO methodology

3 INS的模糊GO法可靠性评价

3.1 系统分析及GO图建立

为验证模糊GO法的有效性，选用平台惯性导航系统(INS)进行可靠性分析研究．某三轴INS基本结构原理图如图2所示，主要组成：①1个三轴惯导平台；②3个高精度加速度计；③3个高精度陀螺仪；④稳定回路，包括前置放大器、数字控制器、功率驱动和力矩电机等；⑤3个旋转变压器；⑥导航计算机；⑦控制显示器；⑧电源等．

图2 某三轴INS基本框图Fig.2 Basic structure schematic of some three-axis INS

根据图2建立INS的GO图，如图3所示．GO图中共有29个操作符和29个信号流，其中操作符代表具体元件，信号流代表具体物流．电源是INS的唯一输入单元，可用类型5操作符(单信号发生器)模拟；陀螺仪、加速度计会由于热冲击、电磁辐射等一些不恰当的动作或不期望的外界刺激产生提前输出，可用类型3操作符(触发发生器)模拟；力矩电机可能因电机线路短路等原因出现提前启动的情况，也可用类型3操作符(触发发生器)模拟；前置放大器、数字控制器、功率驱动、惯导平台、旋转变压器、导航计算机及控制显示器都假定为两种状态单元，可用类型1操作符(两状态单元)模拟．数字控制器只有同时收到3个前置放大器输出的正确角速度信号，才向功率驱动电路发出有效信号，因此可用类型10操作符(与门)来模拟3个前置放大器之间的逻辑关系．同理，加速度计、力矩电机及旋转变压器输出之间的逻辑关系也可用类型10操作符来模拟．INS各操作符类型、代表的单元及各元件的模糊状态概率(以三角模糊数形式表示)如表1所示．

图3 某三轴INS的GO图Fig.3 GO figure of some three-axis INS

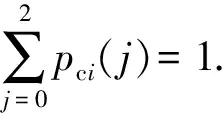
3.2 模糊GO运算

若GO图中存在某信号连接到两个或多个操作符的情况，则该信号定义为共有信号[2]．由图3可知，信号流1、2、3、11、19均为共有信号．由于包含同一共有信号流的信号流之间并不是完全独立的，在定量计算系统状态概率时，需对含有共有信号的信号流进行修正．在用概率公式算法计算时，将含有共有信号的各状态概率表达式展开，把共有信号的高次项修正为一次项，修正后的各状态概率表达式表示正确的状态概率[2]，修正后的关键信号流表达式如下：

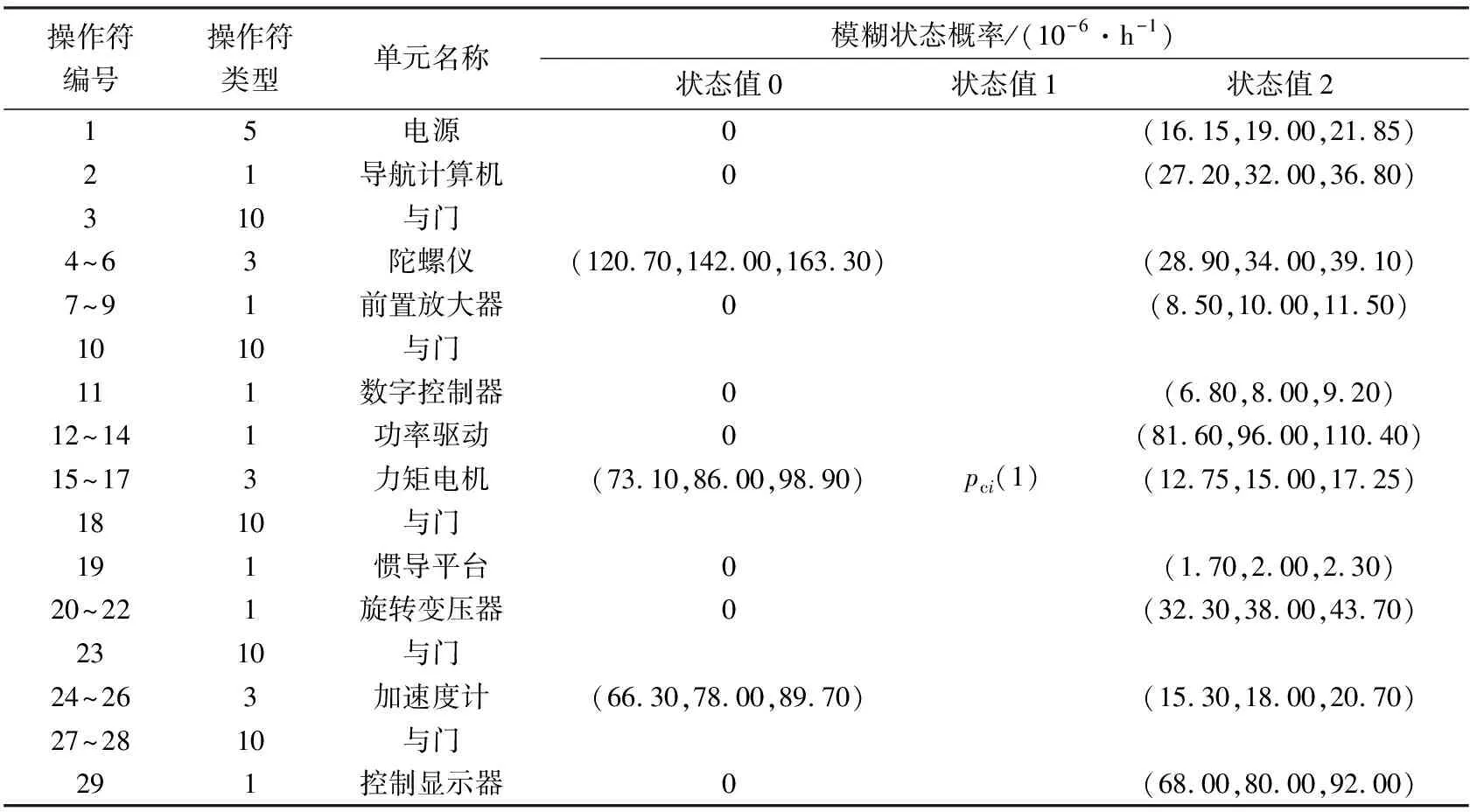
表1 GO操作符及相应的模糊状态概率

信号流3

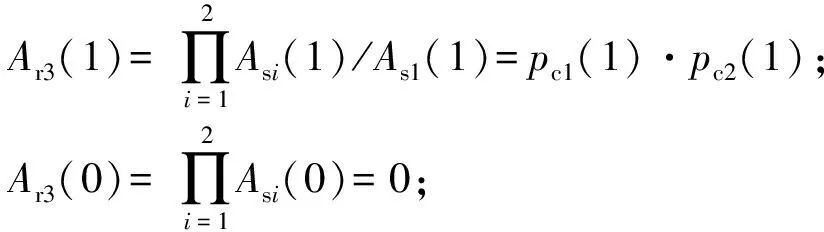
pr3(1)=Ar3(1)-Ar3(0)；

pr3(0)=Ar3(0)=0

(5)

信号流10

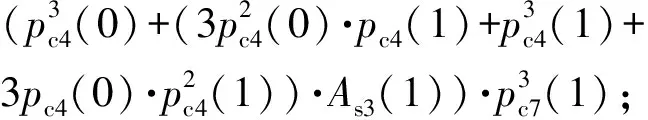
pr10(1)=Ar10(1)-Ar10(0)；

(6)

信号流18

3pc15(0)·(pc14(1)·pc15(1))2·As11(1)；

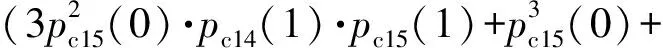
3pc15(0)·(pc14(1)·pc15(1))2+

(pc14(1)·pc15(1))3)·As11(0)；

pr18(1)=Ar18(1)-Ar18(0)；

pr18(0)=Ar18(0)

(7)

信号流23

pr23(1)=Ar23(1)-Ar23(0)；

pr23(0)=Ar23(0)

(8)

信号流27

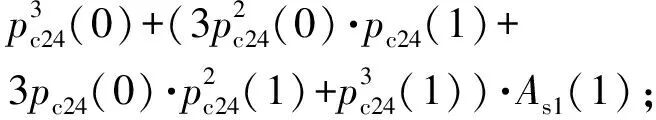
pr27(1)=Ar27(1)-Ar27(0)；

pr27(0)=Ar27(0)

(9)

信号流29

Ar29(1)=Ar28(1)·pc29(1)；

Ar29(0)=Ar28(0)·pc29(1)=0；

pr29(1)=pr28(1)·pc29(1)=

As1(1)·(a27+b27)·pc29(1)；

pr29(0)=pr28(0)·pc29(1)=0

(10)

其中

pc15(1))3+3pc15(0)·(pc14(1)·pc15(1))2，

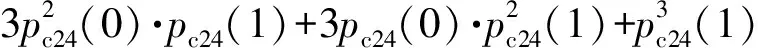
Ari(j)表示输出信号流i的状态值从0到j的状态累积概率；Asi(j)表示输入信号流i的状态值从0到j的状态累积概率；pri(j)表示编号为i的信号流输出状态j的概率；a10、b10、a18、b18、a27、b27均与共有信号无关．

3.3 系统可靠性评价

由GO图可知，信号流29所具有的可靠性特征量表征惯性导航系统的可靠性特性．式(10)中pr29(0)是系统输出模糊状态0的表达式，表征系统输出提前信号的可靠性特性，由pr29(0)=0可知，INS不存在输出提前状态的情况．式(10)中pr29(1)是INS输出模糊状态1的表达式，表征系统输出模糊成功信号的可靠性特性．根据表1中数据、系统输出模糊状态1的表达式及扩展原理，用参数规划方法，借助Matlab可得出直观的INS输出模糊成功概率的隶属度函数，如图4所示．

由图4知：INS输出的模糊成功概率所有可能的取值均在由α=0所确定的区间[0.998 835 16，0.999 617 58]，区间边界值0.998 835 16 和0.999 617 58分别为INS输出的模糊成功概率的最小可能值和最大可能值；0.999 226 30 为INS输出的模糊成功概率的最可能值，对应于隶属度α=1.0的结果．若将α-截集作为系统模糊区间的置信程度，由模糊集合的截集可知，α-截集的取值越小，系统可靠度的模糊区间越大，数据在模糊区间的离散度越大，分析结果的可信度越低；α-截集的取值越大，系统可靠度的模糊区间越小，数据在模糊区间离散度越小，可靠性分析结果的可信度越高．可从决策者偏好的角度取α=0.5，表示中立偏好(neutral attitude)可信，得系统可靠度的置信模糊区间为[0.999 030 71， 0.999 421 92]．

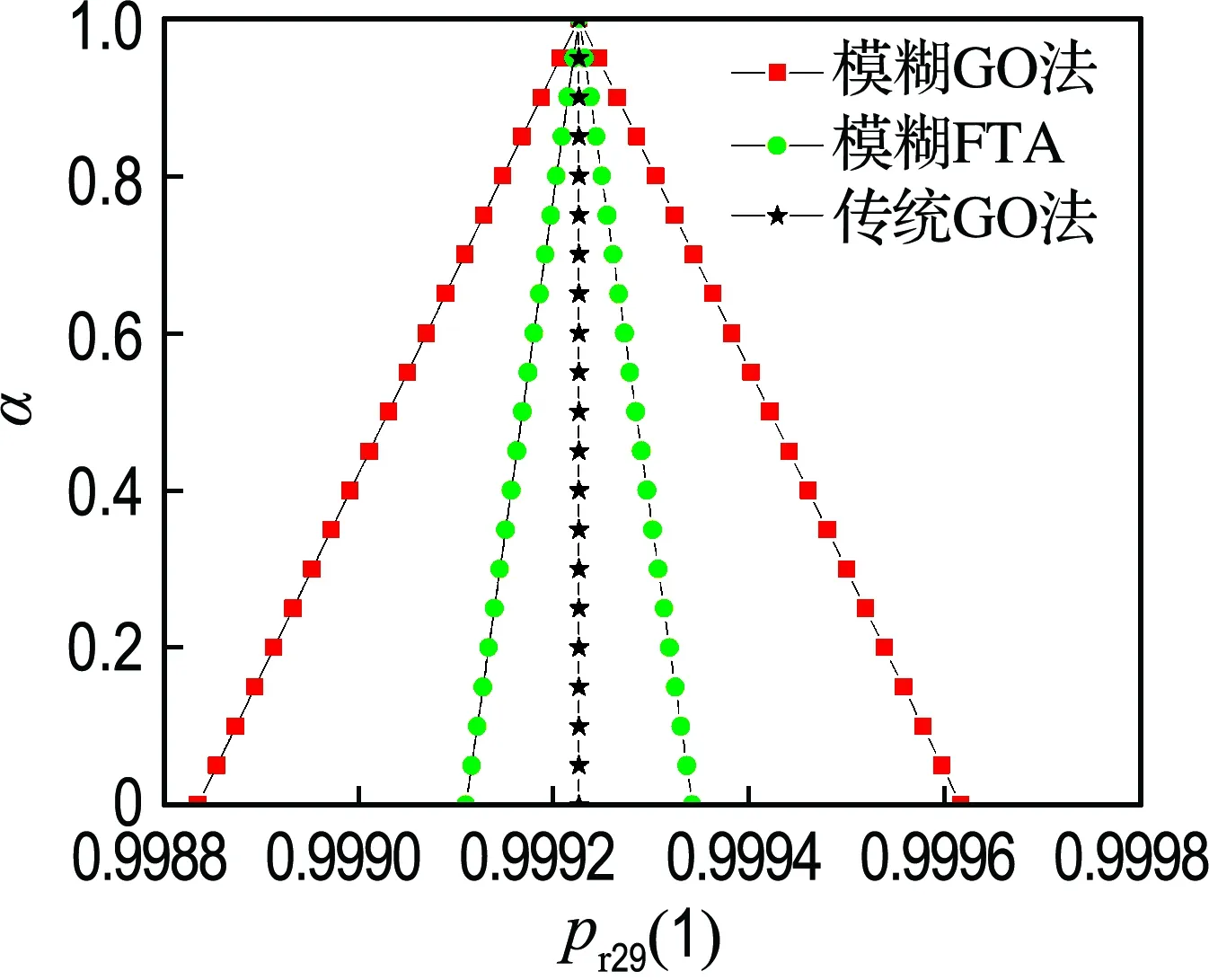
图4 模糊成功概率的隶属度函数Fig.4 Membership function of fuzzy successful probability

4 基于模糊FTA的INS可靠性分析

为验证模糊GO法的有效性，采用文献[19]提出的模糊FTA对INS进行可靠性分析，分析时假设：①各事件只存在成功和故障两种状态；②各事件相互独立；③不考虑人为故障和诱发故障．以控制显示器不能成功输出姿态角和加速度信息为顶事件，建立故障树，如图5所示．

图5 某三轴INS的FTA图Fig.5 FTA figure of some three-axis INS

在FTA图中以Xi表示各底事件，对底事件赋予模糊概率值，模糊数据见表2．由INS原理图可知，任何一个元件故障都会导致顶事件发生，故该故障树中的最小割集为{X1}，…，{X23}；由文献[19]可知，该故障树顶事件发生的概率为

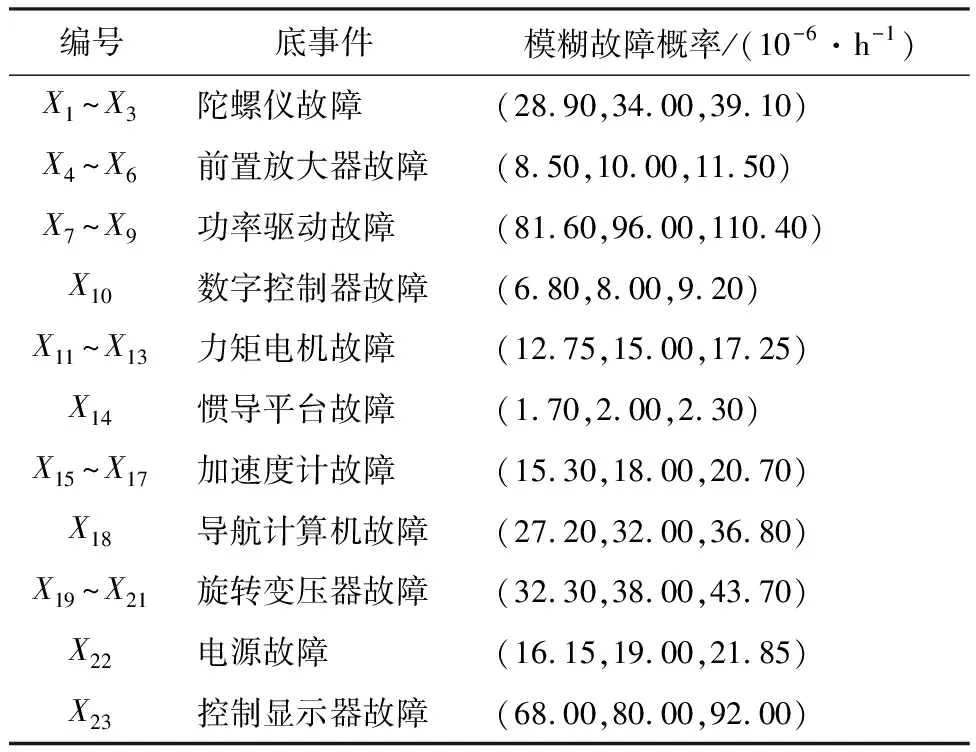
表2 底事件模糊数据

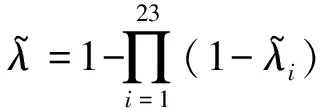
λ～=1-∏23i=1(1-λ～i)

(11)

式中：

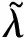
5 3种可靠性分析方法对比

用模糊FTA、传统GO法、模糊GO法分析INS系统的可靠性，得出直观的INS输出模糊成功概率的隶属度函数如图4所示，得出的不同截集水平下的系统可靠性指标见表3．

分析表3可知：

(1)用传统GO法得到的系统可靠度，与当α=1.0时用模糊GO法得出的结果相同．因为当α=1.0时，用模糊GO法计算出的系统可靠度对应于当所有元件的状态概率取精确值时得出的结果．

表3 3种分析方法得到的系统可靠性指标

(2)传统GO法计算出的可靠度均在模糊GO法计算出的可靠度置信模糊区间内，这验证了模糊GO法的有效性．

(3)用模糊FTA和模糊GO法得出不同截集水平的可靠度有差异．因为模糊FTA在建模时只考虑各底事件的成功和故障两种状态，而在GO法中还考虑到陀螺仪、加速度计及力矩电机可能存在的提前状态．同样验证了本文所提方法的有效性，能够有效评估多状态元件和系统的可靠性．

(4)基于隶属度函数的模糊区间能将元件和系统的不确定性量化，使得可靠性分析结果具有说服力．

6 结 论

(1)将模糊数学理论引入到基于GO法的系统可靠性分析中，提出了一种模糊不确定性系统可靠性分析方法——模糊GO法．用模糊数来描述元件的状态概率值，可有效解决由于缺乏足够的数据、统计的不确定性、建模的不确定性等因素而导致的概率不确定性问题；用扩展原理将系统的输出状态概率表示为一个新的模糊数，可得到不同截集水平下的可靠度置信模糊区间，将系统输出的不确定性量化，能准确地分析系统的可靠性；运用参数规划的方法可得到直观的系统模糊状态概率隶属度函数，使得系统可靠性分析结果更加直观，且方法思路清晰、简洁方便．

(2)采用模糊GO法研究INS可靠性，经与传统GO法和模糊FTA分析结果对比，验证了模糊GO法有效，可作为一种复杂多态系统可靠性分析方法．

(3)模糊GO法克服了传统GO法中各操作符只能根据元件历史统计值给定一个精确值的不足，可为复杂系统的模糊不确定性分析提供有效且实用的分析工具，有较强的工程实用性．

[1] 冯 静,潘正强,孙 权,等. 小子样复杂系统可靠性信息融合方法及其应用[M]. 北京:科学出版社, 2015.

FENG Jing, PAN Zhengqiang, SUN Quan,etal.MethodsandApplicationsofReliabilityInformationFusionforComplexSystemwithSmallSampleTest[M]. Beijing: Science Press, 2015. (in Chinese)

[2] 沈祖培,黄祥瑞. GO法原理及应用:一种系统可靠性分析方法[M]. 北京:清华大学出版社, 2004.

SHEN Zupei, HUANG Xiangrui.PrincipleandApplicationofGOMethodology:ASystemReliabilityAnalysisMethodology[M]. Beijing: Tsinghua University Press, 2004. (in Chinese)

[3] 兰 雪,段富海,桑 勇. GO-FLOW法在飞机EHA可靠性分析中的应用[J]. 北京航空航天大学学报, 2017,43(6):1264-1270.

LAN Xue, DUAN Fuhai, SANG Yong. Application of GO-FLOW methodology in reliability analysis of aircraft EHA [J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2017,43(6):1264-1270. (in Chinese)

[4] 樊冬明,任 羿,刘林林,等. 基于动态贝叶斯网络的可修GO法模型算法[J]. 北京航空航天大学学报, 2015,41(11):2166-2176.

FAN Dongming, REN Yi, LIU Linlin,etal. Algorithm based-on dynamic Bayesian networks for repairable GO methodology model [J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2015,41(11):2166-2176. (in Chinese)

[5] 江秀红,段富海,陈 璞,等. 基于GO法和RCM的惯性导航系统预测维修平台设计[J]. 兵工学报, 2014,35(9):1443-1450.

JIANG Xiuhong, DUAN Fuhai, CHEN Pu,etal. Design of predictive maintenance platform for INS based on GO methodology and RCM [J].ActaArmamentarii, 2014,35(9):1443-1450. (in Chinese)

[6] 陈 洁,陈国明,李新宏,等. 深水关井作业可靠性贝叶斯-GO法分析[J]. 中国安全科学学报, 2016,26(4):144-149.

CHEN Jie, CHEN Guoming, LI Xinhong,etal. Reliability analysis of deep-water shut-in operation using Bayesian GO approach [J].ChinaSafetyScienceJournal, 2016,26(4):144-149. (in Chinese)

[7] 张 萌. 统一模糊可靠性模型理论研究及叶片抗振模糊可靠性评估建模[D]. 西安:西北工业大学, 2014.

ZHANG Meng. Theoretical study on the unified fuzzy reliability model and reliability assessment modeling of blades to avoid resonance [D]. Xi′an: Northwestern Polytechnical University, 2014. (in Chinese)

[8] BHARDWAJ R K, MALIK S C. Fuzzy reliability evaluation of a fire detector system [J].InternationalJournalofComputerApplications, 2012,43(3):41-46.

[9] LI Yanfeng, HUANG Hongzhong, LIU Yu,etal. A new fault tree analysis method:fuzzy dynamic fault tree analysis [J].EksploatacjaiNiezawodnosc-MaintenanceandReliability, 2012,14(3):208-214.

[10] 张根保,许 智,王国强,等. 基于模糊理论的GO法多时序可靠性分析研究[J]. 机械设计, 2010,27(11):15-18, 72.

ZHANG Genbao, XU Zhi, WANG Guoqiang,etal. Reliability analysis of GO method multi-temporal based on fuzzy theory [J].JournalofMachineDesign, 2010,27(11):15-18,72. (in Chinese)

[11] 张丽娜,李艳军,张 建. 基于模糊GO法的飞机备件支援系统可靠性分析[J]. 科学技术与工程, 2017,17(4):105-109.

ZHANG Lina, LI Yanjun, ZHANG Jian. Research on reliability of aircraft spare parts support system based on fuzzy GO method [J].ScienceTechnologyandEngineering, 2017,17(4):105-109. (in Chinese)

[12] 李玲玲,武 猛,李志刚. 可靠性度量中的不确定信息处理[J]. 机械工程学报, 2012,48(8):153-158.

LI Lingling, WU Meng, LI Zhigang. Uncertain information processing method in the reliability measurement [J].JournalofMechanicalEngineering, 2012,48(8):153-158. (in Chinese)

[14] DING Y, LISNIANSKI A. Fuzzy universal generating functions for multi-state system reliability assessment [J].FuzzySetsandSystems, 2008,159(3):307-324.

[15] DING Y, ZUO M J, LISNIANSKI A,etal. Fuzzy multi-state systems: General definitions, and performance assessment [J].IEEETransactionsonReliability, 2008,57(4):589-594.

[16] ZADEH L A. Fuzzy sets [J].InformationandControl, 1965,8(3):338-353.

[17] ZADEH L A. Fuzzy sets as a basis for a theory of possibility [J].FuzzySetsandSystems, 1978,1(1):3-28.

[18] SHEN Zupei, GAO Jia, HUANG Xiangrui. An exact algorithm dealing with shared signals in the GO methodology [J].ReliabilityEngineeringandSystemSafety, 2001,73(2):177-181.

[19] WANG Daqing, ZHANG Peng, CHEN Liqiong. Fuzzy fault tree analysis for fire and explosion of crude oil tanks [J].JournalofLossPreventionintheProcessIndustries, 2013,26(6):1390-1398.