喷灌喷头抗风调节机制的研究

郑涵午，赵新宇

(南昌工程学院，南昌 330099)

喷灌技术始于19世纪末，具有省水、省工、省地、保土、保肥等优点，但在有风环境下，灌溉的精准性、均匀性难以得到保证[1-3]，喷灌喷头抗风性能的改良对节水灌溉技术来说十分必要。针对喷灌喷头的抗风性能的改进，付志光等通过给喷头添加自适应装置使喷灌喷头能够在有风条件下调节喷射仰角的方式改变喷射射程[4]，其他研究则集中于针对喷灌喷头抗风性的改进基本都是通过调节喷射俯仰角来实现的[5-7]，此种方式虽然能够将喷射水流的射程调节回来，但却忽视了风力作用对水流喷射方向的偏移作用，会使得喷头在工作状态中的喷射水量分布不均匀。针对于此，本文通过计算模拟，提出调节喷头仰角及喷水量，实现喷灌喷头从有风条件下的工作状态到无风条件下工作状态的还原方法，使得喷头在有风条件下仍能有效工作。

1 喷洒水滴的运动方程

喷灌水滴的运动方程[8,9]为：

(1)

(2)

选定阻力系数方程[10,11]：

CD=(24/Re)(1+0.15Re0.687)Re≤1 000

(3)

CD=0.438{1.0+0.21[(Re/1 000)-1]1.25}Re>1 000

(4)

2 有风状态下的喷射改进模型研究

2.1 无风、有风条件下喷头的工作状态分析

当喷头在无风条件下工作时，由喷嘴射出的水流会形成不同粒径的水滴，利用水滴运动方程即可求解不同粒径的水滴的喷洒半径，当单位水量的水滴分布确定之后，即可计算出喷洒域内的水量分布。假设喷头工作压力、工作仰角、转速不变，则喷头在单位转动角度内喷洒出的水量应保持不变，其喷洒水量的函数f应该为θ2的一次函数。喷头转动一个周期，其喷洒域应为一个圆形，其半径R由最大粒径的水滴落地点确定。

当喷头在有风条件下工作时，由喷嘴射出的一组粒径的水滴会同时受到风速的影响，而使各个粒径的水滴依据其粒径大小受到不同的影响。在有风条件下，喷嘴射出的一股水流的喷射方向因与风速方向不恒等，则水滴在运动过程中势必因风速的作用而产生偏移作用，当喷头转动到与风速方向相正交的情况时，风速对此股水流的偏移影响作用最大。

2.2 有风条件下的喷射改进模型

设不同粒径所对应的喷射半径在无风条件下为r(di)，有风条件下为R(di)，建立目标函数为：

(5)

依据目标函数式(5)，在不同的位置，即不同的θ2处可以计算出喷头所对应的最佳的工作仰角，使得喷头在有风条件下各个水滴粒径的喷洒半径调整回与无风条件下时基本一致。

(2)针对风速对水滴产生的偏转影响的调整。若以风速指向为 轴正向，当喷头工作由x轴正向运动到y轴正向时，在调整射程之后，通过减少喷头喷水量来调节偏转影响，此时，设无风条件下喷洒域接收水量的平均水深函数为F(θ2)，有风条件下调节仰角之后的水深函数为F′(θ2)，Δθ2i(i=1,2,3,…,n)为无风条件下对应的喷洒域的区间，Δθ2j(j=1,2,3,…,n)为相应在有风条件下的喷洒域的区间。

无风条件下，喷头喷洒水量的函数和实际喷洒域接收到的水量有如下关系：

f(Δθ2i)=F(Δθ2i) Δθ2iR2/2

(6)

有风条件下，风力对水滴产生偏移作用，喷水量函数始终保持不变，但此时喷水量函数与喷洒域接收的水量函数有如下关系：

f(Δθ2i)=F′(Δθ2j) Δθ2jR2/2

(7)

当区间Δθ2i确定之后，根据水滴运动方程，可以计算出对应的Δθ2j，建立调节函数为：

f(Δθ2i)=F(Δθ2j) Δθ2jR2/2

(8)

式中：Δθ为喷洒区间的弧度值；R为喷头在一定压力下的射程。

由式(8)即可使得有风条件时的接收水量近似地调节回无风条件时的情况。

3 调节机制的计算验证

为了便于计算，我们将喷洒的水作离散化处理，假定喷洒水滴存在d1=1 mm，d2=1.5 mm，d3=2.0 mm，d4=2.5 mm，d5=3 mm，5种不同粒径的水滴，qi为di直径水滴占总水量的含量，则有关系式q1+q2+q3+q4+q5=1。

3.1 无风条件下喷洒规律

根据喷洒水滴的运动方程，令风速为零，则可以得出无风条件下的水滴的运动规律。根据所给出的初始条件，假定喷嘴距地面高度为0.6 m，喷头工作压力为25 m，水柱近似为25 kPa；θ1=23°，θ2=45°。依靠前面所给出的水滴运动方程式，可以求出不同粒径水滴落地位置与喷头位置关系。取第1象限为例，数据见表1。

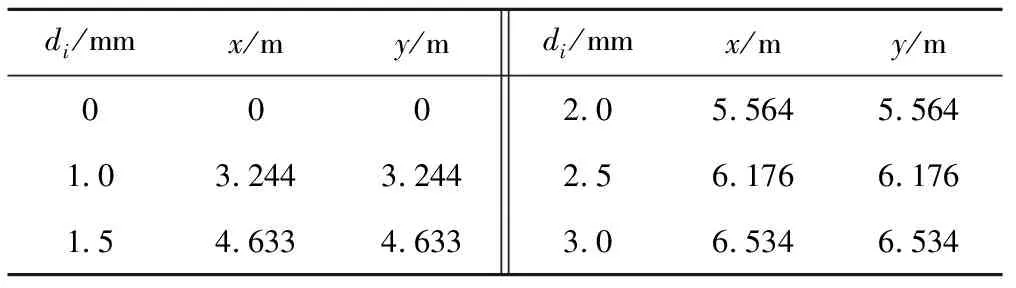
表1 无风条件下水滴射程计算值Tab.1 The calculated and measured value for the range of droplet under no wind condition

3.2 有风条件下喷洒规律

通过喷洒水滴运动方程，给定与无风条件下相同的初始条件，可以求出有风条件下不同粒径水滴的落地位置，假设风速为1 m/s，风向为横轴正方向，其他初始条件同前述无风情况，可以求出各种粒径水滴的落地位置，数据见表2。

表2 有风条件下水滴射程计算值Tab.2 The calculated and measured value for the range of droplet under windy condition

3.3 无风与有风的对比验证

由图1可以比较直观地发现，风速对水滴射程有明显的影响，同时对定时刻的水流有明显的偏转作用。

图1 有风与无风条件下水滴落地点位置对比Fig.1 Comparison of drip site locations in wind and no wind conditions

3.4 按照调节机制的改进方案

根据以上分析，无风条件与有风条件情况存在偏差。首先通过调节俯仰角θ1，可以改变不同粒径水滴的喷洒距离，使有风条件下的不同粒径水滴射程尽量达到与无风条件下一致，求得最优的俯仰角θ1。在上述有风与无风的基本条件下，由式(5)，可写出下式：

(9)

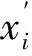
求得在θ2=45°情况下最优的θ1为52°。在θ1为52°的有风条件下求得不同粒径水滴落地距离。

表3为有风条件下调节仰角后的射程计算值。由表3和表1的对比可得，在θ2=45°时，将仰角调节至52°可使得喷头在有风条件下各个粒径水滴的喷射半径基本与无风条件下相同。但此时有风条件下的分布情况较于无风条件下有一定的偏移，若是按照原始的水量喷洒，则由前文分析可知，水量在喷洒域内的分布有明显差异。此时通过调节喷头在转至各个位置时的喷水量来克服这一障碍。

表3 水滴射程计算值(调节后)Tab.3 The calculated and measured value for the range of droplet (After regulation)

设喷灌喷头从x轴转过θ，一定压力下最远射程为R，当转速不变的情况下，喷头所射出的流量Q=kθ，k为一确定常数，其喷洒覆盖区域一定为θ，此时，设最佳仰角为θ1，由水滴运动方程，可求出θ2=θ时对应的有风情况下各粒径水滴的分布曲线，此时其喷洒覆盖区域一定不等于θ，假设为θx，计算Qx=kθx，将Q改变为Qx即可保证此时刻在θx范围内总水量和无风条件下情况一致。由于每一个θ2的位置都能对应一个最佳的θ1，则在进行第2步改进，即改变喷水量时，尽量使得θ→0，这样可以使得改进更加优良。

4 结 语

水滴在空气中的运行轨迹可以用前人所推导的水滴运动微分方程式来表达。根据喷头在喷洒过程中，在一个方向上的喷水总量固定不变的规律，通过有风与无风条件下的喷散射程的计算，并将2种条件下计算结果进行分析，发现通过改进喷头的调节机制，利用改变喷头俯仰角和喷水量的方法，达到与无风条件下喷散状态的相似，从而优化喷灌的性能。

：

[1] 张新华.有风条件下PY1-30型单喷头喷洒湿润图形的变化规律[J].喷灌技术，1985，(1)：8-10.

[2] 喻黎明,牛文全.风对喷灌质量及工程设计的影响研究[J].干旱地区农业研究,2011,29(5):151-155.

[3] 史少培，谢崇宝，高 虹，等.喷灌技术发展历程及设备存在问题的探讨[J].节水灌溉,2013,(11).

[4] 付志光，叶邦彦，韦水平，等.反馈式自适应抗风喷灌节水喷头的研制[J].机械制造与自动化,2007,(2):43-45,50.

[5] 黄修桥，仵 峰，范永申.喷头仰角调节机制的研制及其对喷头性能的影响[J].排灌机械，2006，24(5)：29-32.

[6] 李金山，郭志新，杨跃辉.不同仰角状况下喷头性能试验研究[J].中国农村水利水电，2011,(7)：24-26.

[7] 李星恕,张建宾,韩文霆.仰角可调摇臂式喷头水力性能试验[J].农业机械学报，2015,(2)：34-39.

[8] 张志宇,侯晓宇,侯国恩.由室内试验资料推求有风条件下的喷灌均匀度[J].河北农业大学学报,2013,36(4):132-137.

[9] 黄修桥.有风时的喷洒水滴运动规律及风对喷头射程的影响[J].灌溉排水,1992,(2):1-7.

[10] 白 更，严海军.空气阻力系数对水滴运动及蒸发的影响[J].水利学报，2011,(4)：27-32.

[11] Kincaid D C. Spray drop kinetic energy from irrigation sprinklers[J].Transactions of ASAE 1996,39(3):847-853.