善借“前”概念构建“新”概念
莫远珍
【摘要】本文论述教师要善于借用“前”概念,引领学生合理转变,对其展开纠正、厘清和整合,通过合理的概念转换,最终实现对“新”概念的正确构建。
【关键词】小学数学 概念构建 “前”概念 教学方式
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2018)02A-0048-02
在小学数学教学中,学习新概念之前,大多数学生其实已经对所学的内容有了基本的认识。这些认识是自己的一些观点和看法。这些看法有对有错,有显性也有隐性,我们将其称之为“前”概念。在教学实践中,笔者发现这些“前”概念对学生构建“新”概念既能形成干扰,也能起到推动和促进作用,对学生学习新知具有一定的辅助作用。因此,教师要善于利用“前”概念,引导学生对其进行纠正、厘清和同化,通过合理的概念转换,让“前”概念为“新”概念服务,帮助学生构建正确的、科学的“新”概念。
一、立足纠正,善用“前”概念铺垫“新”概念
在课堂教学中,学生原有的认知和新知之间往往有不一致的情况,这就需要教师提前了解并做出分析,立足对学生的“前”概念进行纠正,激发学生的参与意识,使学生重新认识并改变自己的观点,达到认知平衡,为“新”概念的学习做好铺垫。
如在教学人教版四年级下册《三角形的稳定性》时,教学前大部分学生都会有一个错误的认知:认为长方形的门窗都是固定的,所以长方形也具有稳定性。为此,笔者设计了这样的教学环节:给学生准备了一个三角形和一个长方形的框架,让学生动手拉一拉,看看有什么发现。学生得出结论:长方形容易变形,而三角形不容易变形。这个结论的得出,挑战了学生已有的认知,一部分学生产生了疑问。此时,笔者让学生拿出课前准备的三根小棒和四根小棒,分别摆出一个三角形和一个四边形,看看有什么新发现?学生通过动手操作,发现用三根小棒摆出的三角形只有一种形状;而用四根小棒摆出的四边形,有多种形状,大小也不一样。这个现象说明了什么问题呢?学生通过思考后,认为三角形具有稳定性,而且是唯一性;而四边形则不具备这些特点。
以上环节,教师立足对“前”概念的错误认知进行纠正,为学生创设了认知探究的操作情境,为纠正和完善“新”概念做好了铺垫。值得一提的是,对于学生错误的“前”概念,教师要通过课堂生成对其进行纠正,为新知的构建设置有效的铺垫。
如在教学五年级上册《平行四边形的面积》时,要求出如图1所示的平行四边形的面积,学生列出了两种不同的方法:第一种是5×3=15(平方厘米);第二种是5×4=20(平方厘米)。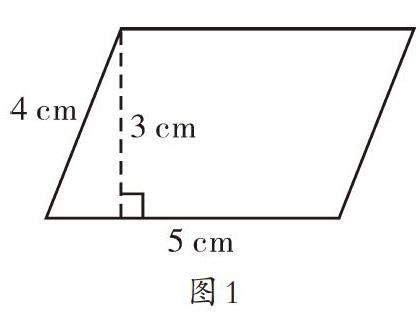
从学生的求解过程及答案中我们可以看到,学生的错误在于没有弄清楚平行四边形的面积到底和什么有关?有什么样的关系?于是,笔者让学生利用学具展开探究。学生认为,要将平行四边形转换为长方形,沿着平行四边形的高剪下,采取剪切—移动—拼接的方法,将平行四边形转化成与其面积相等的长方形。此时长方形的长相当于平行四边形的底边,长方形宽相当于平行四边形的高。根据长方形面积公式可以得出平行四边形的面积公式为底乘以高。
教师通过学生之间的合作、操作和交流,让学生借助自主探究消除了平行四边形的面积与邻边有关的错误的“前”概念认知,为构建平行四边形的面积与底边和高有关的“新”概念认知做足了铺垫。
二、立足厘清,善用“前”概念构建“新”概念
学生在构建“新”概念之前,需要对“前”概念有一个转变的过程。教师要立足对“前”概念进行厘清的过程,给予足够的耐心及充足的时间和空间,等待学生模糊的“前”概念浮现,使“新”概念的认知获得长足发展。
如在教学六年级上册《圆的认识》这一内容时,通过学情测试,笔者发现大部分学生对圆这个图形都有了一定的认识和了解,但这些认识也仅限于圆的基本特征,对圆的本质属性知道的却很少,尤其对用圆规画圆与定点和定长有什么关系这个概念非常模糊。为此,笔者设计了这样的教学环节:让学生准備直尺,用两种不同的方法画圆(如图2)。方法一:先在纸上画出一个点,然后从这个点出发,画出无数条2厘米长的线段,用曲线将这些端点接起来。
方法二:先测量一段4厘米长的线段,将这条线段作为一个圆的直径,并找到这条线段的中点,以这个点为圆心,然后以这条线段的长度为周长作无数个正方形,这无数个正方形围成了一个圆。通过这个操作活动,学生厘清了对圆的已有认知,发现圆有定点和定长这两个基本要素,并且逐渐认识到,圆上的所有的点到定点的距离都相等,这就为学生构建圆的本质属性打下坚实的基础,为“新”概念的生长提供了“养料”。
另外,教师还要根据学生的“前”概念,了解学生真实的知识起点和思维起点,在此基础上实施教学,实现“新”概念的科学构建。如在教学四年级上册《垂直与平行》时,笔者先让学生在白纸上任意画出两条直线(如图3所示),思考:下图中哪两条直线是互相垂直的?结果有一大半的学生认为只有图3-2是互相垂直的。原因是,大部分学生认为只有竖着的一条直线才是互相垂直。为此,笔者让大家仔细观察图3-2和图3-3,比较两条直线之间的关系。有的认为图3-2两条直线是直的,而有的认为图3-3两条直线是斜的。笔者追问:那么图3-3的两条直线到底是不是互相垂直呢?通过辨析和观察之后,学生发现,互相垂直取决于两条直线相交后的夹角是不是直角,和两条线是否倾斜没有直接关系。
由此,通过厘清学生“前”概念中的认知错误和思维错误,让学生在解决问题的过程中逐步形成正确的“新”概念。
三、立足整合,善用“前”概念深化“新”概念
“新”概念的构建是一个新旧认知交替作用的过程,教师可以立足概念整合,利用学生的“前”概念进行比较,帮助学生深入理解“新”概念,进而对“新”概念的本质有更深刻的认识。
如针对教材中一些容易混淆的概念,教师要根据学生的“前”概念,引导学生展开比较和辨析。在教学二年级下册《锐角和钝角》时,笔者通过学情测试,发现学生对角的大小基本上能够正确判断,但是却不能运用专业术语来表述。于是,笔者设计了这样的教学环节:先让学生复习直角,构建直角的概念,并拿出直角器让学生观察,紧接着拿出锐角和钝角学具,让学生以直角器作为参照物,进行比对测量,学生发现比直角小的角是锐角,比直角大的角是钝角。通过这样比较,学生能够在整合“前”概念的基础上,深入“新”概念的本质,清晰地建立角的概念,同时也提升了学生的数学思维能力。
另外,当学生在“前”概念的基础上构建了正确的“新”概念后,教师还要给学生留出一个消化的过程,让学生整合和巩固“新”概念,将所学概念运用在实际生活中,构建富有张力的概念体系。
如在教学三年级下册《面积与面积单位》时,在学生对面积单位有了正确的认知后,笔者让学生从身边的物体开始估测,看看学校的面积怎么求,用什么面积单位;家里房间的面积是怎么求的,估测一下是多少,用什么面积单位?这样的活动激活了学生的“前”概念,为下一步深入探究“新”概念开启新旅程。
教师将概念引向运用环节,有助于学生解决和思考实际问题,同时学生的“前”概念和“新”概念也能有机整合,架构一个有机的知识体系。
(责编 林 剑)

