浸没管对喷动床内颗粒运动和换热的影响及管壁磨损的数值模拟

李 斌， 马梦祥， 张 磊， 于 洋， 陈翠玲

(华北电力大学 能源动力与机械工程学院，河北保定 071003)

喷动床具有良好的传热传质特性，在化工、燃烧、制药、农业等工业领域有着广泛应用[1]。喷动床内的颗粒会在高速气流下发生剧烈碰撞，并与床内气体产生强烈耦合，因此喷动床成为颗粒换热、高温蓄热等方面的重要选择。喷动床内颗粒进行换热时，为了使颗粒的受热更加均匀，通常会在喷动床内加入浸没管，强化床内颗粒之间的碰撞。浸没管会与颗粒频繁碰撞，由此产生的磨损不仅会缩短浸没管的寿命，也会对颗粒的换热产生一定影响。因此，研究带有浸没管的喷动床内颗粒换热特性和浸没管磨损特性具有重要意义。

研究人员对带有浸没管的喷动床进行了换热、磨损等研究[2-4]，但由于实验条件和测量仪器等方面的限制，目前难以获得丰富的颗粒尺度上的信息，对深入研究喷动床内稠密气固两相流动和传热的相关特性也产生了一定阻碍。随着计算机技术的快速发展，数值模拟逐渐成为研究喷动床内颗粒运动、换热特性的主要手段，由Cundall等[5]提出、经Tsuji等[6-7]发展的离散单元法(DEM)具有精确模拟和获得丰富颗粒尺度信息等优点，得到了更多的应用。

杨世亮等[8]和Yang等[9]基于DEM数值模拟方法对鼓泡床内气固两相流的运动特性和浸没管的磨损进行了研究，重点分析了管束排列方式对流动和磨损的影响。虞育松等[10]研究了埋管数量对鼓泡床内颗粒运动的影响，认为增加埋管数量会降低颗粒平均速度和混合效果。任立波等[11]研究了在不同风速下埋管对流化床内颗粒运动的影响，发现提高风速和加入埋管有助于颗粒的混合。Zhao等[12]对流化床内浸没管管壁磨损进行了研究，提出了非法向碰撞磨损的计算模型。Hau等[13]研究了流化床内颗粒大小、浸没管温度等对颗粒-浸没管换热的影响。赵永志等[14]研究了浸没管附近颗粒传热系数的周向分布。杨世亮等[15]研究了埋管与颗粒的传热系数随时间的变化规律。以上研究大多将浸没管作为一种热源来探究颗粒与管壁之间的换热，但几乎没有关于浸没管对喷动床内颗粒换热特性影响的研究，在加入非热源浸没管时，这种影响就必须予以考虑。

笔者将计算流体力学与离散单元法(CFD-DEM)相结合，应用自主开发的程序对带有浸没管的喷动床内颗粒换热与管壁磨损进行数值研究。分别将有、无浸没管时床内颗粒的运动、换热特性进行对比，分析浸没管对喷动床内稠密气固两相流动和传热相关特性的影响，最后从颗粒尺度上对浸没管管壁的磨损进行定量分析。

1 数学模型

1.1 气相运动与传热模型

采用Navier-Stocks方程和湍流运动的k-ε两方程来描述气相运动[16]，并通过添加能量方程来求解气相换热：

(1)

ST=Qg,p/cp,g

(2)

(3)

1.2 固相运动与传热模型

1.2.1 固相运动模型

采用软球模型来描述颗粒相，其受力主要包括来自气体的曳力、自身的重力和颗粒间(包括壁面、管壁)的碰撞力等，采用文献[16]～文献[18]中提出的曳力模型来计算第i个颗粒受到的曳力Fy,i。当网格内的空隙率εg>0.8时，采用Wen等提出的关联式：

(4)

当空隙率εg≤0.8时，采用Ergun提出的关联式进行计算：

(5)

式中：Rei为第i个颗粒的雷诺数；Cd为单颗粒曳力系数。

当Rei>1 000时，Cd取值为0.44，当Rei≤1 000时，由下式来确定Cd：

(6)

当浸没管的尺寸明显大于网格尺寸时，应将其视为壁面，否则应视为一个颗粒[19]。由于浸没管的直径仅为网格尺寸的3倍左右，因此将其视为一个质量为无穷大的颗粒，其与颗粒的碰撞可视为2个异径颗粒间的碰撞。

1.2.2 固相传热模型

流化床内的颗粒传热主要包括与气体的对流换热、与颗粒(包括壁面、管壁)的碰撞换热以及与周围环境的辐射换热。

颗粒与气体的对流换热采用下式进行计算：

Qi,g=hi,convAi(Tg-Ti)

(7)

hi,conv=Nuiλg/di

(8)

(9)

式中：hi,conv为气体与颗粒之间的对流传热系数；Ai为颗粒的表面积；Tg为第i个颗粒所在网格内的气体温度；Ti为第i个颗粒的温度；λg为气体的导热系数；di为第i个颗粒的直径；Rei为第i个颗粒的雷诺数；a为修正系数，取值为1.2[16,20]。

经验关联式的系数很大程度上取决于实验条件，但目前还没有能够精确求解出气体和颗粒间对流传热系数的通用关联式。

一般认为颗粒与颗粒间(壁面)的碰撞换热主要通过变形颗粒的接触面进行，分为2种方式，即颗粒之间无相对速度的静止接触传热和具有相对速度的碰撞导热[16,20]，可分别按式(10)和式(11)进行求解：

(10)

(11)

式中：Qi,j为颗粒i、j间的导热换热量；λp为颗粒导热系数；rc为颗粒接触半径；tc为颗粒碰撞时间；cp为颗粒比热容，ρp为颗粒密度；T为颗粒温度；c为修正系数，可通过一系列关联式来确定[16,21]。

在颗粒碰撞过程中，如果接触时间td小于碰撞时间tc，则认为碰撞过程中只进行碰撞传热；否则认为在碰撞传热结束后的时间内(td-tc)还进行静止接触传热。笔者假定接触时间td与时间步长Δt相等。

文献[16]和文献[20]中指出，在床层温度较低的情况下，与其他2种换热方式相比，颗粒与周围环境的辐射换热对颗粒总换热量的贡献很小，考虑到模拟中可能出现的最高温度仅为500 K，因此忽略颗粒与周围环境的辐射换热。

颗粒温度在多种传热方式的共同作用下不断发生变化，遵循的能量方程为：

(12)

式中：mi为第i个颗粒的质量；Qi,wall为第i个颗粒与壁面的换热量；ki为与第i个颗粒发生碰撞换热的颗粒数量。

假定浸没管与颗粒、气体均不进行换热，因此仅研究浸没管对床内颗粒换热的影响。

1.3 气固两相耦合作用

气相对固相的作用力和传热分别通过计算曳力和对流换热得到，固相对气相的反作用分别通过式(13)和式(14)进行计算：

(13)

(14)

式中：Fp、Qg,p分别为固相对气相的作用力和固相对气相的传热量；ΔV为单个网格的面积。

2 模拟对象及参数

2.1 模拟对象

模拟对象为150 mm×4 mm×900 mm的单喷口矩形截面喷动床，网格尺寸为10 mm×4 mm×10 mm；在床底部正中间布置进气口，尺寸为10 mm×4 mm。2个浸没管的圆心位置及编号如图1所示，管径为28.28 mm。

图1 喷动床几何尺寸

笔者采用适体网格进行模拟。喷动床出口采用局部单向化条件，气相在近壁面处采用无滑移边界条件。固相采用2 400个直径为4 mm的球形颗粒。

2.2 模拟参数

对带有浸没管的喷动床内颗粒换热和管壁磨损进行数值模拟。通过自然堆积得到颗粒初始位置，颗粒和气体的初始温度均为300 K，喷入的高速射流温度恒定为500 K，在整个模拟过程中壁面温度均设为定值300 K,气相和颗粒相的基本模拟参数见表1。

表1 模拟基本参数

3 模拟结果

3.1 喷动床内颗粒流动及传热序列图

图2给出了表观气速v为2.2 m/s、模拟时间t为0～2 s时不含浸没管和含有浸没管的喷动床内颗粒流动及传热过程序列图。在2种工况下，随着高温气流的喷入，位于喷口附近的颗粒首先被加热，并受到来自气体的曳力作用而上升；位于床层顶部壁面附近的颗粒在重力的作用下落至底部，填补上升颗粒留下的空缺。到达顶部的上升颗粒逐渐向两侧壁面流动，成为下落颗粒，而落至底部的下落颗粒被高温气流卷吸成为上升颗粒，并被加热。床内颗粒在上升与下落之间反复变化，形成了喷动床内颗粒的循环流动与传热过程，这一现象也得到证实[16]。

(a) 不含浸没管

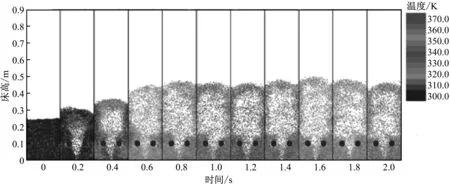
(b) 含有浸没管

在颗粒的循环流动与传热过程中，床内颗粒的温度迅速升高，而颗粒的温度分布较为均匀，这是因为颗粒-气体的对流传热与颗粒-颗粒的碰撞换热扮演不同的角色。一方面，喷入的高温气体是喷动床内的唯一热源，因此颗粒的温升全部来自颗粒-气体的对流换热；另一方面，颗粒间进行频繁的碰撞换热，不同温度的颗粒相互交换热量，使得颗粒的温差减小。

为了对模型和数值模拟结果的准确性进行验证，笔者针对不含浸没管的工况进行了实验研究，具体实验条件与数值模拟设定的条件相一致，并将模拟和实验颗粒流动的瞬时图进行对比，如图2(c)所示。由图2可以看出，在床内颗粒喷动流化的不同阶段，颗粒流动和分布、气泡的生成和分布等方面的模拟与实验结果吻合度较高，说明采用的数值模拟程序能较准确地反映出喷动床内的实际情况，在此基础上开展的研究具有较高的可信度。

3.2 浸没管对喷动床内颗粒运动特性的影响

(15)

式中：n为床内总颗粒数；hi为第i个颗粒的竖直高度。

由图3可以看出，在0～2 s内，喷动床不含浸没管时颗粒平均高度存在较大波动，在0.84 s时达到最大高度(0.225 m)，随后迅速下降，在1.22 s时降至0.188 m，说明在0.38 s内颗粒平均高度下降了约0.04 m，下降速度达到0.1 m/s，在1.72 s左右颗粒平均高度重新稳定在0.2 m附近，进入相对稳定的喷动流化过程。在同一时间段内，当喷动床内含有浸没管时，在0.84 s时颗粒平均高度达到约0.2 m,后有小幅波动，进入到相对稳定的喷动流化阶段，其所需时间比不含浸没管时减少了约一倍。

图3 颗粒平均高度随时间的变化

颗粒平均高度主要受颗粒竖直方向速度的影响。图4为喷动床内颗粒平均竖直速度随时间的变化曲线。颗粒平均竖直速度定义为：

(16)

式中：vi为第i个颗粒在竖直方向上的速度。

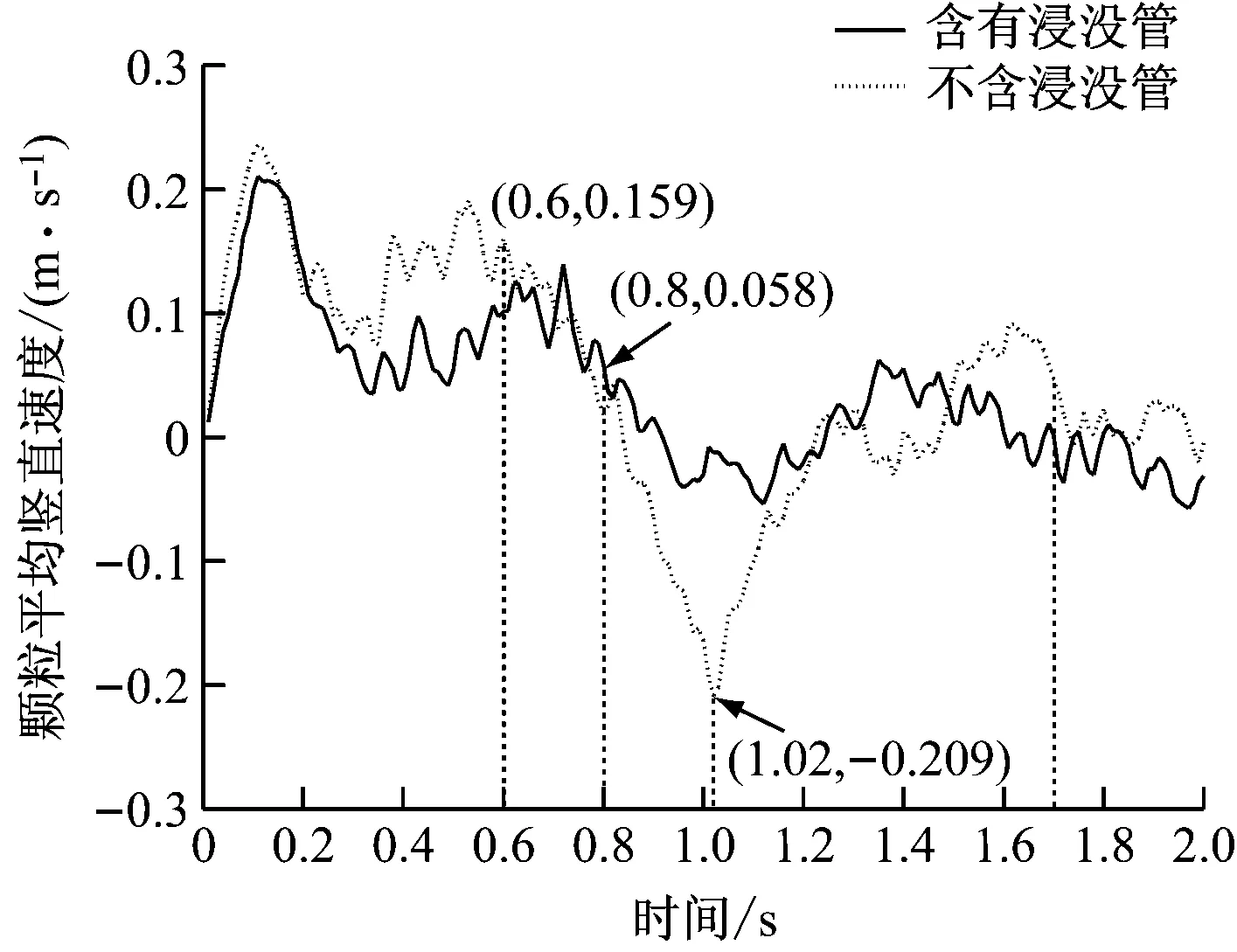
图4 颗粒平均竖直速度随时间的变化

由图4可以看出，当喷动床不含浸没管时，在0.6 s颗粒平均竖直速度在0.4 s内从0.1 m/s迅速降至最低(-0.2 m/s)，导致颗粒平均高度迅速降低，之后颗粒平均竖直速度快速提高，在1.7 s左右才相对稳定。在整个过程中，颗粒平均竖直速度的变化幅度超过0.3 m/s。在同一时间段内，当喷动床内含有浸没管时颗粒平均竖直速度的波动相对较小，0.8 s后在0附近进行窄幅震荡，其振幅为0.15 m/s。

综上，浸没管对床内颗粒的运动起到阻碍作用。当颗粒受到气体的曳力向上运动时床层膨胀，颗粒与浸没管的碰撞使得颗粒损失一部分动能，因此床层膨胀速度和高度均降低。当颗粒受到重力作用回落时，其与浸没管的碰撞会阻碍颗粒向下回落，使得床高可在较短时间内迅速稳定。

3.3 浸没管对喷动床内颗粒传热的影响

(17)

式中：Ti为第i个颗粒的温度。

由于颗粒的温升均来自于颗粒-气体的对流换热，所以颗粒-气体的对流传热系数对颗粒温升有重要影响。

图6为颗粒-气体平均对流传热系数随时间的变化曲线。由图6可以看出，当喷动床内含有浸没管时，颗粒-气体的对流传热系数要显著高于不含浸没管的情况。浸没管会阻碍其下方区域内颗粒的向上运动，增加颗粒在底部的停留时间，并增大该区域内颗粒的密度。在这一区域内，气体具有较高的温度和较大的速度，因此颗粒与气体间的对流传热系数较高，颗粒平均温度也高于不含浸没管的情况。

图5 颗粒平均温度随时间的变化

图6 颗粒-气体平均对流传热系数随时间的变化

图7为床内颗粒温度方差随时间的变化曲线。床内颗粒温度方差s2定义为：

(18)

图7 颗粒温度方差随时间的变化

当床内含有浸没管时，颗粒温度方差在0.4 s左右达到7 K2后，在该值附近进行窄幅震荡，方差相对稳定；当床内不含浸没管时，颗粒温度方差不会稳定在某值附近，而是随时间不断增大。因此，浸没管可显著减小颗粒温度的方差，使床内颗粒温度分布更加均匀。

添加浸没管会导致喷动床内的几何结构更加复杂，颗粒间的碰撞次数也会增加。采用基于颗粒尺度的离散单元法可得到颗粒间相互碰撞的信息。不含浸没管时，在0～2 s内颗粒间的总碰撞次数为2 575 920；加入浸没管后，总碰撞次数增加了26 400，这有助于不同温度的颗粒之间交换热量，使得温度分布更加均匀。

综合上述分析，浸没管有助于强化喷动床内颗粒-气体的对流换热，提高颗粒平均温度，使颗粒温度分布更加均匀。

3.4 喷动床内浸没管磨损分析

由于浸没管与颗粒频繁地碰撞，因此管壁磨损是不可忽视的问题。国内外学者通常采用Finnie[22]提出的磨损模型定量考察喷动床内球形颗粒对管壁的磨损情况。在不同碰撞角度下的磨损量E为：

(19)

(20)

式中：PH为浸没管材料的维氏硬度，取为294 MPa；mp为撞击颗粒的质量；vp为颗粒的撞击速度；γ为颗粒的碰撞角度，定义为颗粒撞击速度与碰撞点处切线方向的夹角。

图8给出了喷动床内2根浸没管在0～ 2 s内的磨损情况。由图8可以看出，浸没管1的最大磨损量出现在约165°处，这主要是喷动区的高速颗粒与管壁的直接碰撞造成的。次大磨损量出现在0°附近，这是因为床层顶部颗粒在沿壁面下落的过程中与管壁碰撞，颗粒的下落速度较小，因而造成的管壁磨损量也较小。浸没管2的磨损量分布与浸没管1近似呈对称分布，这与2根浸没管在床内的对称布置有关。整体来看，喷动床内浸没管的磨损主要发生在管壁下方，靠近壁面处的管壁磨损情况相对较好，这与文献[15]中的结论一致。

4 结 论

(1)浸没管对颗粒的竖直方向运动有重要影响。浸没管阻碍了颗粒沿竖直方向的运动，使得颗粒竖直方向的速度波动减小，床高波动也随之减小，喷动床内建立稳定喷动流化过程所需的时间相应缩短。

(2)浸没管对喷动床内颗粒的换热过程有显著影响。浸没管增加了颗粒与高温高速气体接触的时间，强化了颗粒-气体对流换热，提高了床内颗粒的平均温度，同时使床内几何结构更为复杂，增加了颗粒间的相互碰撞，使颗粒的温度分布更加均匀。

(3)浸没管的管壁磨损来自于颗粒与管壁间的高速碰撞，其磨损量沿周向有较大变化。在管壁下方靠近中心喷口一侧(约165°)，由于颗粒速度较大，所以磨损情况最严重，而靠近壁面一侧(约270°)颗粒速度较小，因此磨损情况也相对较好。

：

[1] 郭慕孙, 李洪钟. 流态化手册[M]. 北京: 化学工业出版社, 2008.

[2] 吴新, 王亚欧, 李俊. 内循环流化床内置床换热器传热特性试验研究[J].中国电机工程学报,2016, 36(8): 2181-2187.

WU Xin, WANG Ya'ou, LI Jun. Experimental study on heat transfer in an in-bed heat exchanger of an internally circulating fluidized bed[J].ProceedingsoftheCSEE,2016, 36(8): 2181-2187.

[3] LYCZKOWSKI R W, BOUILLARD J X, GAMWO I K, et al. Experimental and CFD analyses of bubble parameters in a variable-thickness fluidized bed[J].Industrial&EngineeringChemistryResearch,2010, 49(11): 5166-5173.

[4] JOHANSSON K, NORLING R, HJÖRNHEDE A, et al. Hydrodynamics and steel tube wastage in a fluidized bed at elevated temperature[J].ChemicalEngineeringScience,2004, 59(1): 31-40.

[5] CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J].Géotechnique,1979, 29(1): 47-65.

[6] TSUJI Y, TANAKA T, ISHIDA T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe[J].PowderTechnology,1992, 71(3): 239-250.

[7] TSUJI Y, KAWAGUCHI T, TANAKA T. Discrete particle simulation of two-dimensional fluidized bed[J].PowderTechnology, 1993, 77(1): 79-87.

[8] 杨世亮, 罗坤, 房明明, 等. 不同管排方式下三维鼓泡床内气固流型及埋管磨损的LES-DEM研究[J].工程热物理学报,2014, 35(7): 1338-1342.

YANG Shiliang, LUO Kun, FANG Mingming, et al. LES-DEM investigation of the hydrodynamics and tube erosion in 3-d bubbling fluidized beds with different tube configurations[J].JournalofEngineeringThermophysics,2014, 35(7): 1338-1342.

[9] YANG Shiliang, LUO Kun, FAN Jianren, et al. Particle-scale investigation of the hydrodynamics and tube erosion property in a three-dimensional (3-D) bubbling fluidized bed with immersed tubes[J].Industrial&EngineeringChemistryResearch,2014, 53(17): 6896-6912.

[10] 虞育松, 张衍国, 李清海, 等. 基于DEM的埋管鼓泡流化床内颗粒运动特性模拟[J].清华大学学报(自然科学版),2012, 52(1): 72-76.

YU Yusong, ZHANG Yanguo, LI Qinghai, et al. DEM simulation of the behavior of particles in a spout-fluid bed with immersed tubes[J].JournalofTsinghuaUniversity(ScienceandTechnology),2012, 52(1): 72-76.

[11] 任立波, 韩吉田, 赵红霞. 单沉浸管流化床内离散颗粒数值模拟[J].浙江大学学报(工学版),2015, 49(1): 150-156.

REN Libo, HAN Jitian, ZHAO Hongxia. Numerical simulation of discrete particles in fluidized bed with immersed tube[J].JournalofZhejiangUniversity(EngineeringScience),2015, 49(1): 150-156.

[12] ZHAO Yongzhi, XU Lei, ZHENG Jinyang. CFD-DEM simulation of tube erosion in a fluidized bed[J].AIChEJournal,2016, 63(2): 418-437.

[13] HAU Zhongyuan, LIM E W C. Heat transfer from an immersed tube in a bubbling fluidized bed[J].Industrial&EngineeringChemistryResearch,2016, 55(33): 9040-9053.

[14] 赵永志, 江茂强, 郑津洋. 埋管流化床内不同粒径颗粒传热行为的欧拉-拉格朗日模拟研究[J].高校化学工程学报,2009, 23(4): 559-565.

ZHAO Yongzhi, JIANG Maoqiang, ZHENG Jinyang. Eulerian-Lagrangian simulation of the heat transfer behavior of particles with different diameters in fluidized bed with immersed tube[J].JournalofChemicalEngineeringofChineseUniversities, 2009, 23(4): 559-565.

[15] 杨世亮, 罗坤, 张科, 等. 三维流化床内埋管传热及磨损特性的LES—DEM研究[J].工程热物理学报,2013, 34(11): 2081-2085.

YANG Shiliang, LUO Kun, ZHANG Ke, et al. LES-DEM study on heat transfer and erosion patterns of immersed tube in 3D fluidized bed[J].JournalofEngineeringThermophysics, 2013, 34(11): 2081-2085.

[16] 周遵凯. 喷动床内气固两相流流动与传热特性研究[D]. 北京: 华北电力大学, 2015.

[17] 李斌, 周遵凯, 姚路, 等. 流化床内不同密度颗粒流动特性的数值模拟[J].动力工程学报,2014, 34(12): 932-937, 971.

LI Bin, ZHOU Zunkai, YAO Lu, et al. Numerical simulation on flow characteristics of different density particles in a fluidized bed[J].JournalofChineseSocietyofPowerEngineering,2014, 34(12): 932-937, 971.

[18] 张俊强, 纪律, 李斌, 等. 双孔射流流化床内颗粒混合特性的离散单元法数值模拟[J].动力工程学报,2017, 37(2): 91-97.

ZHANG Junqiang, JI Lü, LI Bin, et al. DEM simulation on mixing characteristics of particles in double jets fluidized bed[J].JournalofChineseSocietyofPowerEngineering,2017, 37(2): 91-97.

[19] HOU Qinfu, ZHOU Zongyan, YU Aibing. Gas-solid flow and heat transfer in fluidized beds with tubes: effects of material properties and tube array settings[J].PowderTechnology,2016, 296: 59-71.

[20] ZHOU Zongyan, YU Aibing, ZULLI P. Particle scale study of heat transfer in packed and bubbling fluidized beds[J].AIChEJournal, 2009, 55(4): 868-884.

[21] ZHOU J H, YU Aibing, HORIO M. Finite element modeling of the transient heat conduction between colliding particles[J].ChemicalEngineeringJournal,2008, 139(3): 510-516.

[22] FINNIE I. Erosion of surfaces by solid particles[J].Wear,1960, 3(2): 87-103.