基于SD模型的重庆市水资源承载力模拟分析
李 玲,潘雪倩,夏威夷,孙林博,雷孝章
(四川大学水利水电学院水力学与山区河流开发保护国家重点实验室,成都 610065)
0 引 言
水是万物之源。地球上水资源很丰富,但可供人类利用的淡水资源非常有限。在经济和人口增速较缓的时代,供水压力较小,人们错误地以为“水是取之不尽用之不竭的”,没有意识到水资源是大自然赐予人类的宝贵财富[1]。而在人口膨胀、经济快速增长的今天,水资源问题已成为制约地方经济发展的一大阻力。根据2012年的统计,目前我国约有2/3的城市缺水,约1/4的城市严重缺水。水资源问题关乎社会能否可持续发展,是我国发展道路上必然面对、必须解决的。因此,开展水资源承载力的研究,对社会经济的可持续发展具有重要意义。
水资源承载力尚未有统一明确的概念20世纪80年代,新疆水资源软科学课题组首次开启了水资源承载力的研究,认为水资源承载力为区域内可利用水量所能够撑起的最大人口、经济规模[2]。惠泱河[3]等学者则将水资源承载力定义为:在一定的经济和技术水平下,坚持走可持续发展道路,区域水资源对经济发展的最大支撑能力。本文采用新疆水资源软科学课题组对水资源承载力的定义,以重庆市为研究区域,运用系统动力学理论建立动态模型,预测2016-2025年重庆市水资源承载力,并根据模拟结果提出改善水资源供需压力的对策。
1 研究区概况
重庆市位于中国西南部,是西南地区综合交通枢纽和最大的工商业城市,是国家重要的现代制造业基地,也是西部开放开发战略支撑和长江经济带西部中心枢纽。总面积8.24 万km2,辖38个区县(自治县),常住人口3 048.43 万。属亚热带季风性湿润气候,降水较丰沛,多年平均降水量在1 200 mm左右,降水时空分布不均匀,空间上东南多西北少,时间上夏秋多冬春少。长江干流自西向东横贯重庆市,还有嘉陵江、乌江等长江一级支流流经,过境客水相当丰富,但利用率较低[4]。2015年重庆市人均水资源量为1 353 m3,根据Falkenmark和Widstrand[5]确定的水资源压力临界值判断,该地区已出现水资源压力。城镇供水压力愈来愈大,水资源短缺问题愈发严峻,或将成为制约重庆市经济社会发展的一大因素。
重庆市直辖后,由于国家政策扶持,社会经济迅猛发展,城镇化进程加快,水资源需求矛盾日益尖锐。重庆经济发展以工业为主导,工业增加值约占地区生产总值的四成。2015年该地区万元工业增加值用水量为59 m3,略高于全国平均万元工业增加值用水量56.8 m3,经济迅猛发展的同时伴随着水资源的大量消耗;节水灌溉面积较少,粗放式的灌溉方式大量存在。2014年节水灌溉面积仅占有效灌溉面积的28%,农田灌溉有效利用系数仅为0.48,与发达国家的有效利用系数(0.7~0.8)差距较大。 由此可见,重庆地区水资源主要消耗于工业用水和农田灌溉两个方面。
2 重庆市水资源承载力SD模型的构建
系统动力学(SD)由美国麻省理工学院的福瑞斯特(Jay W·rrester)教授于1956年创立。初期主要应用于工业企业管理领域,之后逐渐深入到各种领域。其可在宏观和微观层面上研究复杂、多层次、多部门、非线性的大规模系统[6]。系统动力学最基本的问题为一阶系统,在一阶系统中,状态变量方程式是主干,一般形式为:
LEV.K=LEV.J+(DT)(RT.JK)
(1)
式中:LEV.K、LEV.J为K、J时刻的状态变量;DT为时间间隔;RT.JK为J时刻到K时刻的速率变化向量。式(1)可改写为:
(LEV.K-LEV.J)/DT=RT.JK
(2)
式(2)表明状态变量的变化率等于速率变化值。以上描述的是一阶系统的情况,而高阶系统可以简化为一阶系统或低于四阶的简单系统。可以说,系统动力学模型是由上述向量方程确定的一阶微分方程组[7]。系统动力学有专门的模拟软件,如Anylogic、STELLA/iThink、Powersim、Vensim等。本文使用美国Ventana Systems, Inc.提供的个人学习版Vensim PLE来进行建模,建模步骤见图1。
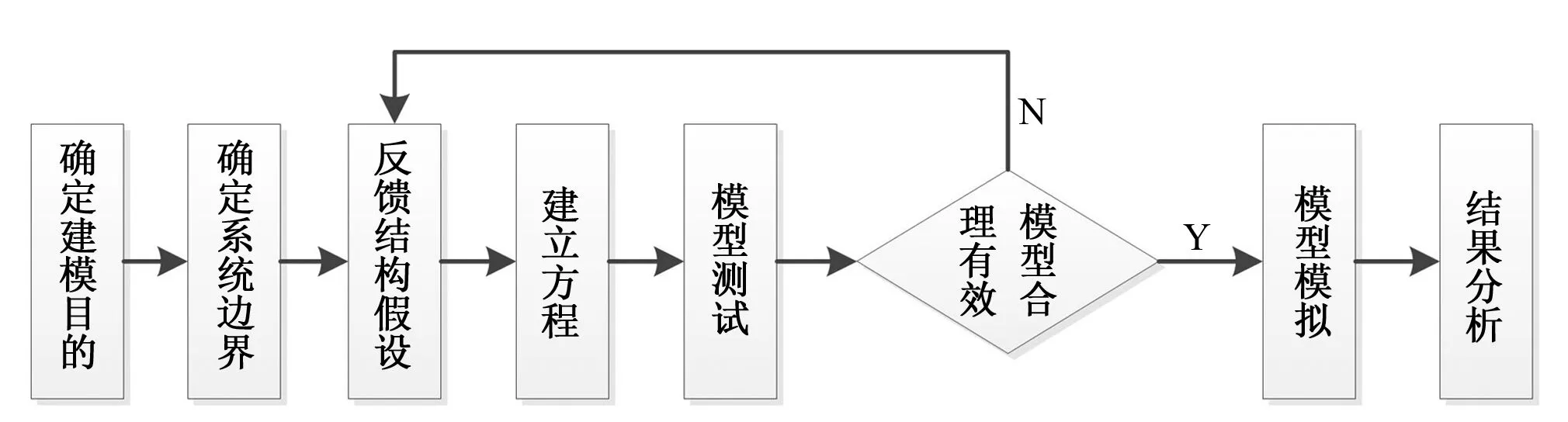
图1 系统动力学建模步骤Fig.1 Steps of system dynamics modeling
2.1 建模目的
本文运用系统动力学方法建立模型,预测重庆市的水资源承载力,分析模拟结果并为重庆市如何缓解水资源供需矛盾提出一些建议。
2.2 数据来源
根据2005-2015年历年《重庆统计年鉴》、《重庆市水资源公报》、《重庆市农业用水定额》等资料设定模型的各个变量取值。
2.3 模型边界
系统动力学通过系统内部变量之间的反馈来分析和解释问题,建模之前首先确定系统边界。在边界内部将与研究对象有动态关系的重要变量归入模型,边界以外的不予考虑[8]。如图2所示,本文所建模型大体分为需水和供水两大模块,需水模块包括生活需水、经济需水和生态环境需水,其中一产需水分为农业需水和牧渔需水;供水部分包括地下水、地表水和中水回用。除了图2中所提及的供需水组成外,其余均不纳入系统界限内。此模型的时限为2005-2025年,其中2005-2015年为历史检验期,2016-2025年为预测时期,模拟步长设为1年。
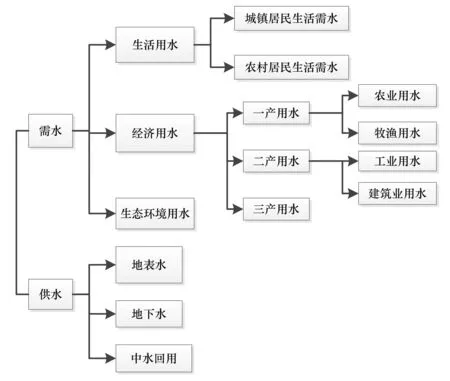
图2 模型结构说明图Fig.2 Model structure diagram
2.4 绘制系统流图
分析了解重庆市水资源承载力系统结构后,通过反复调整,绘制出重庆市水资源承载力系统流图(见图3),模型包括需水和供水两大模块的64个变量。
2.5 模型主要方程
(1)需水模块。需水模块分为生活需水、经济需水、生态环境需水。生活需水包括城镇生活用水量和农村生活用水量;经济需水包括第一产业需水量、第二产业需水量、第三产业需水量,其中第一产业需水量包括牲畜需水量、种植业需水量、渔业需水量,第二产业需水量包括工业需水量和建筑业需水量。需水模块中部分参数的计算方程见表1。
其中,式(1)用表函数表示自然增长率与时间的关系。vensim软件表函数表达形式为:
Y=WITHLOOKUP(X,{[(xmin,ymin)-(xmax,ymax)]
(x1,y1),(x2,y2),…,(xn,yn)})
(3)
式中:X为自变量;Y为因变量;(xn,yn)为包含点的数据;xmin、

图3 重庆市水资源承载力系统流图Fig.3 Flow chart of water resources carrying capacity of Chongqing
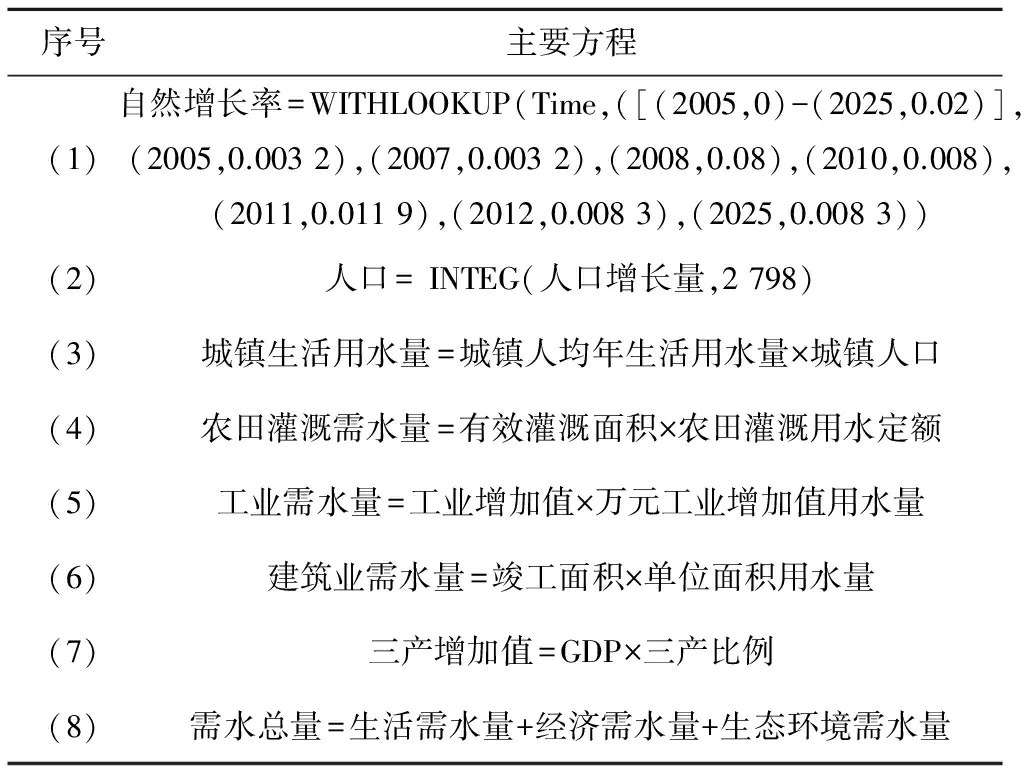
序号主要方程(1)自然增长率=WITHLOOKUP(Time,([(2005,0)-(2025,0.02)],(2005,0.0032),(2007,0.0032),(2008,0.08),(2010,0.008),(2011,0.0119),(2012,0.0083),(2025,0.0083))(2)人口=INTEG(人口增长量,2798)(3)城镇生活用水量=城镇人均年生活用水量×城镇人口(4)农田灌溉需水量=有效灌溉面积×农田灌溉用水定额(5)工业需水量=工业增加值×万元工业增加值用水量(6)建筑业需水量=竣工面积×单位面积用水量(7)三产增加值=GDP×三产比例(8)需水总量=生活需水量+经济需水量+生态环境需水量
(2)供水模块。供水总量包括地下水、地表水、中水利用量。这3个变量均使用表函数进行输入。
(3)水资源供需比。水资源供需比=供水总量/需水总量。
2.6 模型有效性检验
建模后需对其进行检验,确保模型与原系统有较高的相似度,能较好地反映原系统的特征和变化规律,保证模拟结果的可靠性。系统动力学模型的有效性检验方法有直观检验、运行检验、历史性检验、灵敏度分析,本文进行历史检验和灵敏度分析。
2.6.1 历史检验
选取2005-2015年人口、GDP、工业增加值3个关键变量对模型进行检验,以2005年为基准年,预测2005-2015年上述3个变量的估计值,并与真实值对比,相对误差在10%以内,模型有效。通过比较(表2),3个变量的相对误差均在5%以内,精度较高,模型有效。
2.6.2 灵敏度分析
灵敏度分析是通过调整某参数的取值,观察状态变量有无显著的波动,模型行为有无显著差异。若有显著差异,则参数需要准确估计,或者重新调整模型结构。灵敏度S计算公式为:
(4)

由于模型参数较多,选取人口、大牲畜总数、有效灌溉面积、GDP、三产比例5个重要参数进行灵敏度分析。分别对5个参数进行±3%、±5%、±8%、±10%不同幅度的扰动,根据式(3)计算出各参数对需水总量的灵敏度系数[9],变化趋势图见图4。从变化趋势来看,当参数在10%内不同幅度变化时,对应的灵敏度系数变化趋势较缓,即5个参数在10%内变化时,对其灵敏度影响不大;从数值大小来看,敏感度排序为GDP>有效灌溉面积>人口>三产比例>大牲畜总数。根据文献[10]对灵敏度强弱分级(表3)可知,GDP为敏感参数,有效灌溉面积、人口为中等灵敏参数,三产比例、大牲畜总数为低敏感参数。
2.7 情景设计
将水资源承载力系统分为需水和供水两大模块,在情景设计时假定供水情势不变,通过需水总量的变化来设计情景,设计出如下3种情景:
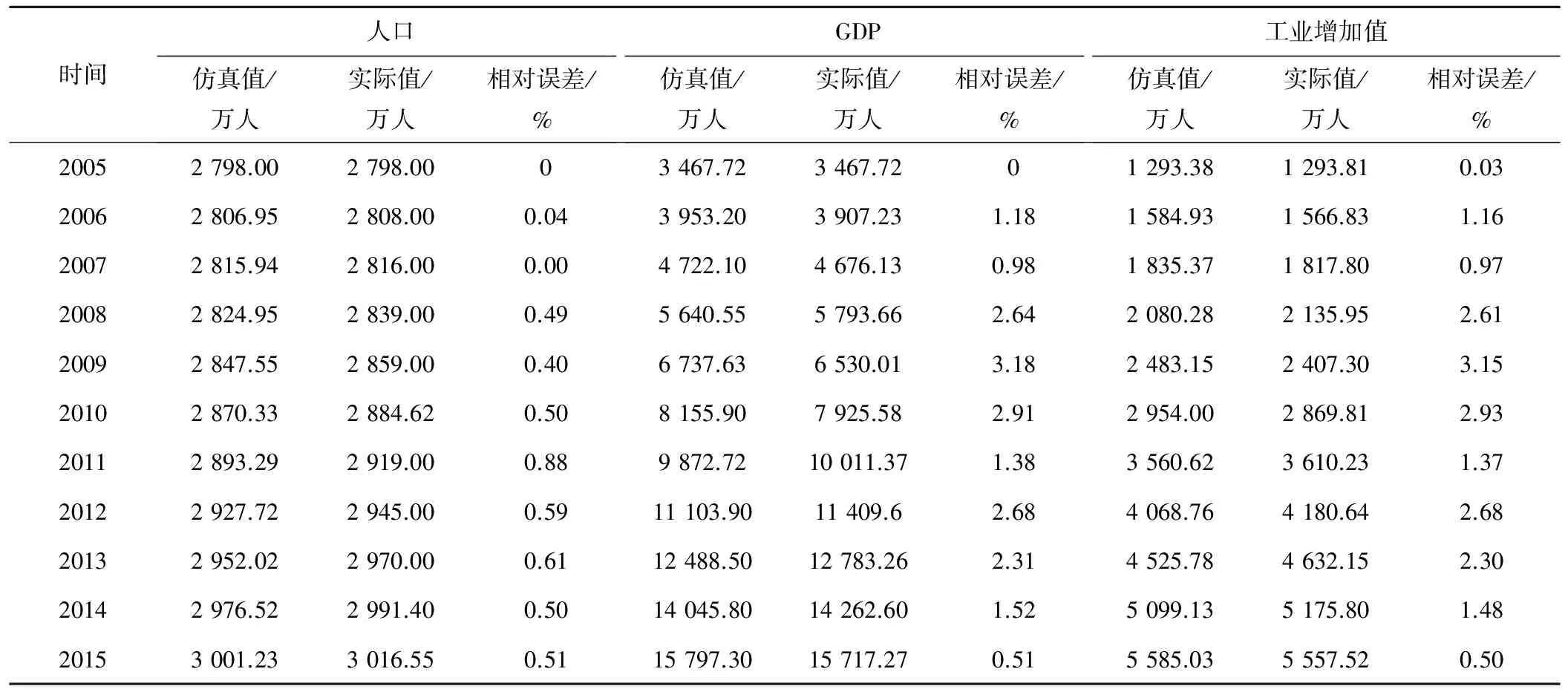
表2 模型历史检验结果Tab.2 Historical test results of SD model

表3 灵敏度分级Tab.3 Classification of sensitivity

图4 参数灵敏度系数变化趋势图Fig.4 Parameters' sensitivity
情景一:现状延续型,各变量保持现有发展趋势不变;情景二:经济发展型, 2012-2015年,重庆市四年平均GDP名义增长率为12%。现假定GDP 名义增长率从2016-2025年保持13.5%不变,其余参数与情景一保持一致;情景三:节水型,主要调整农村生活人均年用水量、城镇生活人均年用水量、农田灌溉用水定额、万元工业增加值用水量等变量,其他变量值与情景一保持一致。
3 情景模拟结果分析
按照上述3种情景调整参数,模拟预测2016-2025年社会经济规模、需水量和水资源供需比。
3.1 社会经济规模
社会经济规模主要取人口和GDP两个指标。3种情景均假设人口增长与历史检验期保持一致,故3种情景下人口预测值相同,变化趋势见图5(a)。到2025年,重庆市人口达到3 250 万人左右,比2015年增加250 万人口。图5(b)为GDP趋势图,到2025年,3种情景下的GDP均在50 000 亿元以上。

图5 社会经济指标模拟结果趋势图Fig.5 Social and economic indicators simulation results
3.2 需水量
需水量包括需水总量、经济需水量、生活需水量、第一产业需水量、第二产业需水量、第三产业需水量6个指标。图6(a)为不同情景下的需水总量,其大小排序为:节水<现状延续<经济发展。到2025年,现状延续型需水总量将达到145 亿m3,经济发展型超过150 亿m3。而节水型,2015-2020年需水总量呈下降趋势,2020年后需水总量逐年增加,2025年仅为100 亿m3,节水效果非常显著。
对比图6(a)、图6(b),经济需水量占需水总量的80%左右,其变化趋势与需水总量基本保持一致;图6(c)显示3种情景下生活用水量逐年增加,人口持续膨胀使得降低居民人均年生活用水量的节水措施效果并不显著;从图6(d)可看出,现状延续和经济发展情景下,第一产业用水量增长率很小但仍保持增加的趋势,采取节水后,第一产业需水量逐年下降。到2025年,节水型第一产业需水量仅比现状延续型、经济发展型约少2 亿m3,节水效果不显著;图6(e)显示,现状延续型和经济发展型的第二产业需水量快速增加。到2025年,现状延续型达到80 亿m3,经济发展型高达85 亿m3以上。而节水型的第二产业需水量先下降后上升,在2025年达到最大值,约比现状延续型减少2倍的需水量,节水效果非常显著;从图(f)看出,经济发展型的第三产业需水量略高于节水型和现状延续型,到2025年,3种情况的第三产业需水量均为2015年的3倍以上。

图6 需水量趋势图Fig.6 Water demand
3.3 水资源供需比
水资源供需比为供水总量与需水总量的比值,供需比<1,说明供求小于需求;供需比>1,说明供求大于需求。从水资源供需比(见图7)来看,在2015-2025年期间,节水型均大于0.8,其中2016-2022年供需比不低于0.9,现状延续型和经济发展型则逐年降低,到2025年,均降至0.6以下。3种情景下水资源供需均未达到平衡,但节水型可以有效地提高水资源供需比。
4 结 语
本文运用系统动力学方法建立重庆市水资源承载力模型,呈现出一个社会、经济、生态环境、水资源等子系统相互影响的有机系统。根据情景设计调整参数,运行模拟得出以下结论。
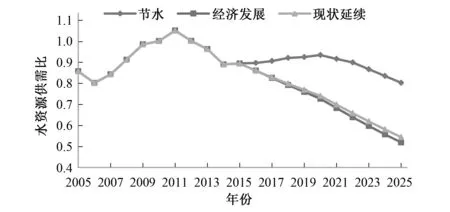
图7 水资源供需比趋势图Fig.7 Water supply and demand ratio
(1)从需水总量来看,到2025年,为撑起3 250 万人口和50 000 亿元GDP的社会经济规模,现状延续型和经济发展型的需水总量均超过了140 亿m3,节水型仅为100 亿m3,节水效果非常显著。
(2)降低居民人均年生活用水量和农田灌溉用水定额,能达到节水目的,但效果不显著;降低万元工业增加值用水量能达到非常显著的节水效果。
(3)由三情景模拟得出的结果可知,水资源承载力大小为节水型>现状延续型>经济发展型。
综上所述,重庆市可以在工业上广泛采用节水型设备、工艺,农业上大力推广管道输水、喷灌等先进灌溉技术,生活上向居民普及节水型器具,进行节水宣传,大力建设节水型社会,改善水资源供需矛盾较尖锐的现状。
□
参考文献:
[1] 贾绍凤. 水资源经济学[M]. 北京:中国水利水电出版社, 2006.
[2] 新疆水资源软科学课题研究组. 新疆水资源及其承载能力和开发战略对策[J]. 水利水电技术, 1989,(6):2-9.
[3] 惠泱河, 蒋晓辉, 黄 强,等. 水资源承载力评价指标体系研究[J]. 水土保持通报, 2001,21(1):30-34.
[4] 张秀江. 重庆水资源现状与可持续利用对策[J]. 土木建筑与环境工程, 2001,23(5):37-40.
[5] 贾绍凤. 中国水资源安全报告[M]. 北京:科学出版社, 2014.
[6] 王其藩. 高级系统动力学[M]. 北京:清华大学出版社, 1995.
[7] 王建华, 江 东. 基于SD模型的干旱区城市水资源承载力预测研究[J]. 地理与地理信息科学, 1999,(2):18-22.
[8] 钟永光, 贾晓菁, 钱 颖. 系统动力学[M]. 2版. 科学出版社, 2013.
[9] 晁 锐, 郭建青, 冯晓旭,等. 推理公式法计算参数的不确定性与灵敏度分析[J]. 人民珠江, 2015,36(4):29-31.
[10] Lenhart T, Eckhardt K, Fohrer N, et al. Comparison of two different approaches of sensitivity analysis[J]. Physics and Chemistry of the Earth, Parts A/B/C, 2002,27(9):645-654.

