基于有效最大含水量的土壤水分监测优化布设方法

王 珊，胡振华，张宝忠，陈 鹤

(1.山西农业大学林学院，山西 晋中 030801；2.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100038；3.国家节水灌溉北京工程技术研究中心，北京 100048)

0 引 言

土壤含水量的准确获取是制定灌溉制度，实现对作物适时适量灌溉的基础。然而，由于农田土壤特性的空间异质性，导致土壤含水量监测点的布设数量与位置对监测精度存在很大影响，因此亟待开展考虑空间变异特点的土壤水分优化布点方法研究。

近年来，国内外许多学者在土壤水分空间变异定量表征[1-5]、土壤含水量监测点合理数目及优化布设位置[6-11]等方面做了大量研究。在空间变异表征方面，申祥民[12]等在新疆以膜下滴灌棉田为研究对象，利用地统计学理论研究土壤含水量变异规律，结果表明土壤含水量在20～40和40～60 cm的空间变异为弱变异，60～80和80～100 cm层的空间变异强度属弱变异及中等变异。M.Herbst[13]等在德国以0.29 km2田块为研究对象，对0～20 cm土层土壤水分的空间变异性进行了研究，在1 hm2内采用10 m×20 m网格取样，结果表明其变异函数符合球状模型，相关距约53.8 m。Wilson D J[14]等在新西兰某流域60 hm2内采用40 m×40 m网格取样，研究了0～30 cm层土壤水分的空间分布，结果表明其变异系数为19%，变异函数符合球状模型，空间相关域为150 m。N.V.Prasolova[15]等利用经典统计学研究了澳大利亚种植夏松地块的土壤水分及氮等元素的时空变异，结果表明采样策略与研究的对象、采样手段等有关。

在布设数量优化方面，李彦[16]等在新疆石河子以滴灌棉田为对象研究发现应用等值线图及地统计学方法，土壤含水量的采样效率比传统统计学方法提高约3倍。张继光、杨贵羽、吴宏平[17-19]等研究发现在确定合理取样数时应同时考虑统计特征和土壤的空间结构性。孙凯[20]等在北京通州区采用经典统计学和地统计学方法研究区域含水量的合理采样数目。陈坤[21]等研究发现在120 m×90 m区域内的膜下滴灌番茄生育期，其平均地块全方向的变程值为23.81 m，在置信水平95%，采样误差5%μ的条件下，合理的采样数目为18～20 个。

在布设位置方面，杨风亮、李芳松[22,23]等研究发现在棉花膜下滴灌田含水量监测点布置在距滴灌带47 cm范围内为宜。Phene[24]等研究发现在滴灌条件下，传感器应该安放在靠近滴头的区域。Stegman[25]等研究表明传感器可以埋设在不同根系分布层，并且较深处传感器埋设深度是较浅处传感器的2倍。Haman[26]等研究发现一般将滴灌传感器放置在作物根系活跃层，且距滴头一定距离时，测墒精度较高。申孝军[27]等利用R型谱系聚类法对滴灌棉田的土壤水分测点布设方案进行研究，发现利用径向上距滴灌带0、32.5和50 cm处观测点以及垂向0～10、20～30、40～50和60～80 cm处观测点的体积含水量可以较好地反映整个土壤剖面的含水量情况。

然而，有关土壤含水量合理采样数目、布设位置的研究多以土壤含水量实测数据为基础确定，每次的实测数据仅能代表这段时期的土壤含水量，多次之间可能存在较大差异，从而导致合理采样点数量和布设不断变化，缺乏通用性。因此，本文提出以土壤有效最大含水量作为关键参数，结合经典统计方法和地统计方法，构建土壤含水量监测优化布设方法。

1 材料与方法

1.1 研究区概况

试验在国家节水灌溉北京工程技术研究中心大兴试验基地(N39°37.25′，E116°25.51′)周边3.645 km2试验区开展。该试验区位于北京市大兴区，属于半干旱大陆性暖湿季风气候，这里四季分明，春季少雨多风，夏季炎热多雨，秋季天高气爽，冬季寒冷少雨，多年平均气温为12.1 ℃，极端温度最高为39.5 ℃，最低为-25 ℃。区内年际间降雨量变化较大，降雨量最大为971 mm，最小为206 mm，年内降雨量分布不均，多年平均降雨为540 mm，降雨多集中在汛期的6-9月份，其降雨量占全年降雨量的80%以上[28]。该区光热自然条件丰富，适合多种作物生长，包括小麦、玉米等。

1.2 测定指标与方法

将3.645 km2试验区划分为162个小区，每个小区范围为150 m×150 m。根据种植结构，本文选择玉米种植的129个小区开展研究，每个小区的采样点按照深度0～20、20～40、40～60、60～80 cm共分4层取样。取0～20和20～40 cm的平均值作为耕作层(0～40 cm)数据，取0～20、20～40、40～60和60～80 cm的平均值作为作物根区(0～80 cm)数据。

1.2.1 土壤有效最大含水量

采用马尔文激光粒度仪(MS2000)对129个小区的分层土样进行颗粒分级分析，根据土样中各粒径颗粒的百分含量后，利用美国土壤质地分类三角表进行土壤质地类型的确定，并采用SPAW[]软件，获得土壤有效最大含水量。

wa=wf-wp

(1)

式中：wa为土壤有效最大含水量，%；wf为田间持水量，%；wp为凋萎系数，%。

1.2.2 土壤含水量

采用烘干法测定129个小区样点的分层土壤重量含水量，25 d左右测定一次，共测5次。

1.3 土壤含水量监测优化布设方法

以土壤有效最大含水量为关键参数，考虑其统计特征和空间结构性，采用经典统计学方法确定某置信度的合理布设数目，根据地统计学方法的变程分析确定取样点布置。

1.3.1 合理布设数目

根据经典统计学方法，在样本数量较多的情况下，可以用样本的数学期望和方差代替总体的数学期望和方差，计算公式如下[30]：

N=(λa·S)2/Δ2

(2)

式中：λα为正态分布特征值；S为样本标准方差；△为采样误差，通常取Δ=kμ，k可取5%、10%、15%、20%等。

如果计算所得出的合理采样数大于样本容量的10%，则应将计算公式转换为不等重复抽样公式再计算抽样数N′：

(3)

式中：N总为样本总数；N为等重复抽样时计算的抽样数。

1.3.2 合理布设位置

根据地统计分析方法，采用半方差函数(空间变异函数)描述土壤特性空间变异结构，计算公式如下：

(4)

式中：γ(h)为区域化变量Z(X)的样本变异函数；h为两样本点空间分隔距离；Z(Xi)和Z(Xi+h)分别是区域化变量Z(X)在空间位置Xi和(Xi+h)的观测值；N(h)为间距为的样本对数。本文采用交叉验证法，根据误差最小原则确定最优半方差函数模型。

应用surfer12.0软件对土壤有效最大含水量进行空间插值，获得土壤有效最大含水量等值线图与平均值，计算每一个插值点处的含水率与平均含水率的相对误差，选择平均相对误差最小的插值点即为最优测墒点，根据半方差函数模型参数变程为基准做出扇形区域与均值线相交选择样点，确定采样点的具体位置。

2 结果与讨论

2.1 土壤有效最大含水量的空间变异特点

2.1.1 正态分布检验

图1是0～40与0～80 cm土壤有效最大含水量的正态分布检验图，可以看出，0～40、0～80 cm深度有效最大含水量数据绝大部分都在45°直线附近，说明它们均服从正态分布。因此，可以应用经典统计学方法分析空间变异和确定合理布设数目。这与之前一些研究有些相似，陈坤[31]和张继光[17]都在研究土壤含水量变异特征过程中发现土壤含水量需满足正态分布。

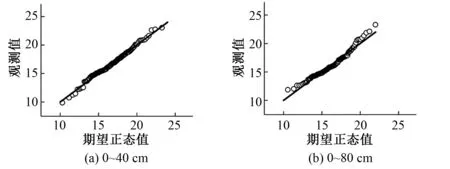
图1 土壤有效最大含水量正态分布检验图(单位：%)Fig.1 Normal test of soil available maximum water content

2.1.2 土壤有效最大含水量空间变异

表1为不同深度田间土壤有效最大含水量统计特征值，表明0～40和0～80 cm深度的土壤有效最大含水量的变异系数分别是14.96%和13.56%，属于中等程度变异。

图2为0～40、0～80 cm土壤有效最大含水量的空间分布图，从图2中可以看出，0～40、0～80 cm的空间分布情况基本一致，在西南-西北方向的土壤有效最大含水量较大，其他地区较小；0～40 cm的土壤有效最大含水量在10%～23%之间变化，0～80 cm深度的土壤有效最大含水量在12%～23%之间变化。

表1 不同深度田间土壤有效最大含水量统计特征值Tab.1 Statistic characters of soil available maximum water content of the different depth

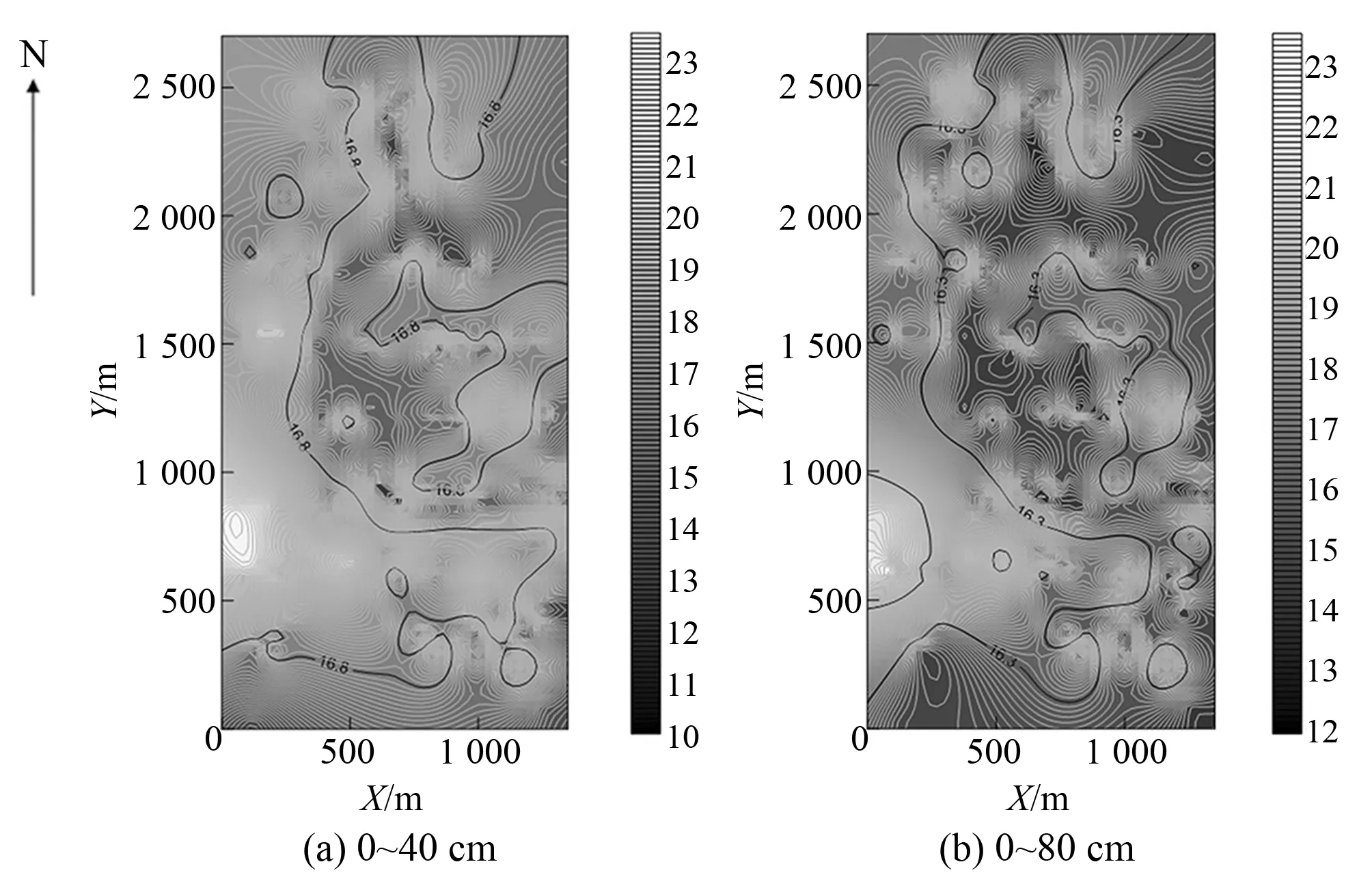
图2 土壤有效最大含水量等值线图(单位：%)Fig.2 Contour map of soil available maximum water content

2.2 土壤含水量监测优化布设数量与位置

2.2.1 半方差函数理论模型

采用交叉验证法检验选择适合的半方差函数理论模型，具体结果如表2和图3所示。由表2可以看出，0～40与0～80 cm深度的半方差函数理论模型都为指数形式，且0～40与0～80 cm深度的块金基台比分别是25.56%、24.51%，0～40 cm表现为中等程度的空间相关性，受随机性因素与结构性因素的共同作用影响，0～80 cm表现为较强的空间相关性，主要受结构性因素的影响。0～40 cm深度变程是780 m，0～80 cm深度变程是1 104 m，在变程范围内的监测点之间具有相关性，在变程范围外的监测点是相互独立。由图3可看出0～40 cm的基台值大于0～80 cm的基台值，0～40与0～80 cm的变异函数值均随着滞后距离的增加先增大后趋于平稳状态。

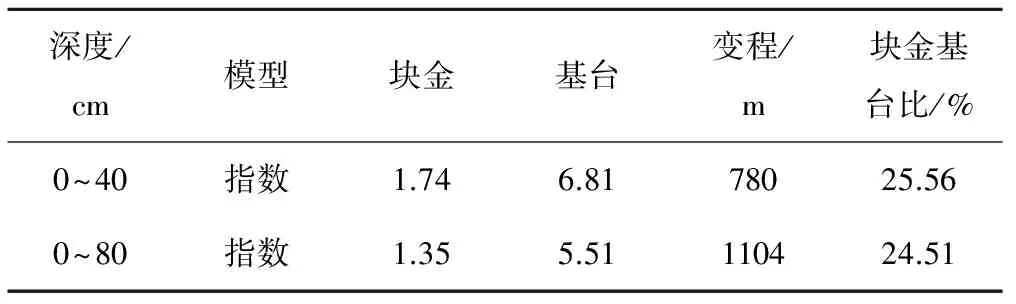
表2 土壤有效最大含水量半方差函数模型参数Tab.2 Semivariogram model parameter of soil available maximum water content

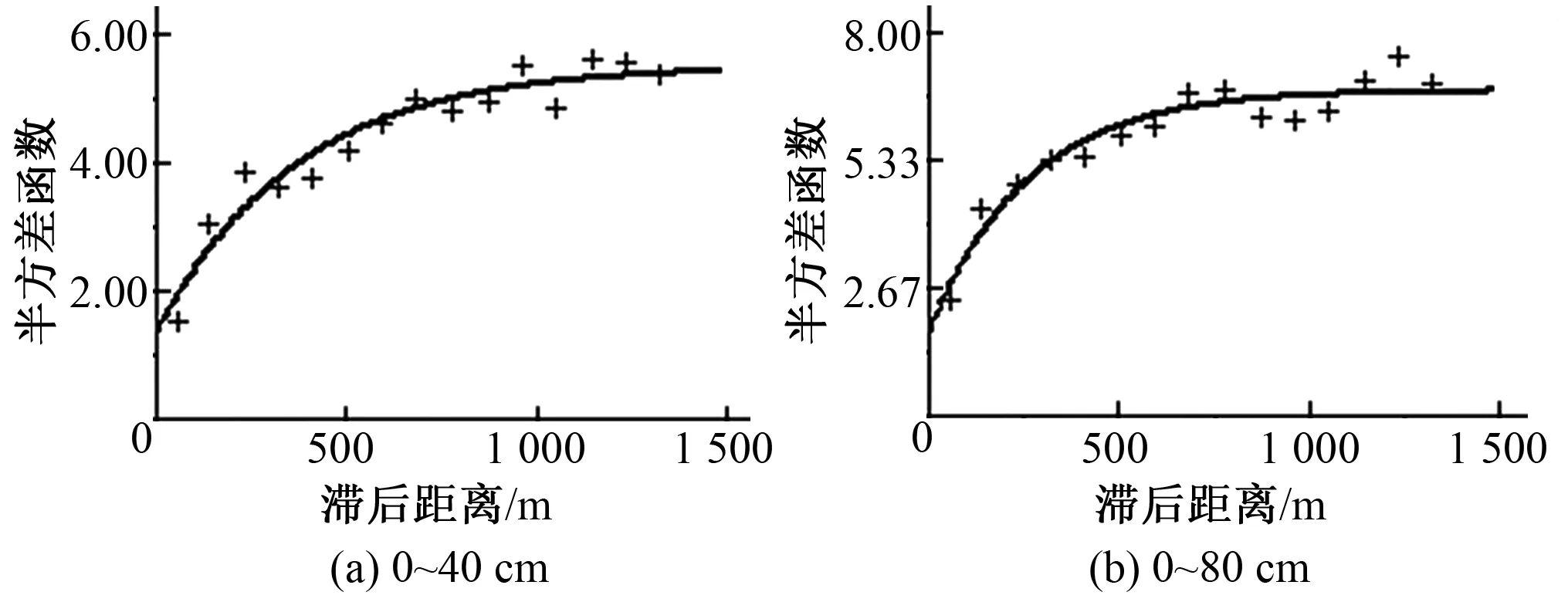
图3 土壤有效最大含水量半方差函数模型Fig.3 Semivariogram model of soil available maximum water content

2.2.2 合理采样数目与位置

根据经典统计方法，取置信区间95%、90%，采样误差取5%、10%、15%、20%，根据式(2)和式(3)确定0～40和0～80 cm深度的合理采样数目见表3所示。在同一置信水平情况下，随着采样误差的增大而采样数目减少；在一定的采样误差条件下，合理采样数目也随着置信水平的降低而逐渐减少。杨诗秀以133 hm2农田为例，研究也表明在置信度p=80%，误差Δ=0.1的条件下，取样数目为10，将采样误差降为0.2时，取样数目为4[32]。

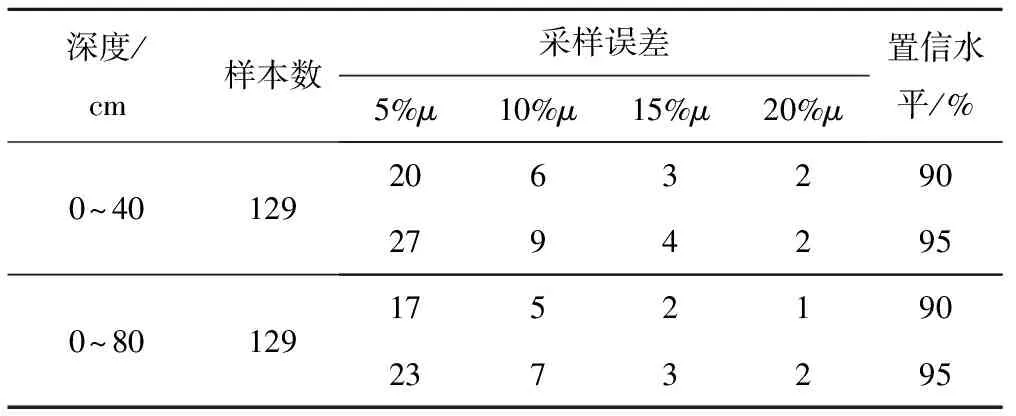
表3 不同置信水平、不同采样误差条件下的合理采样数目Tab.3 The reasonable number of samples under the different confidence level and different sampling error

通过129个样点的土壤有效最大含水量进行空间插值，获得0～40、0～80 cm的空间分布图，根据空间插值获得每个插值点的土壤有效最大含水量值与区域平均值，计算它们的相对误差，选择最小相对误差为最优测墒点，并以半方差函数模型参数变程为基准，在均值线上确定其他采样点的具体位置。试验区的土壤有效最大含水量在90%置信区间，10%的采样误差水平下，0～40 cm深度合理采样点数目为6个，0～80 cm深度合理采样点数目为5个，具体坐标如表4和图4所示。

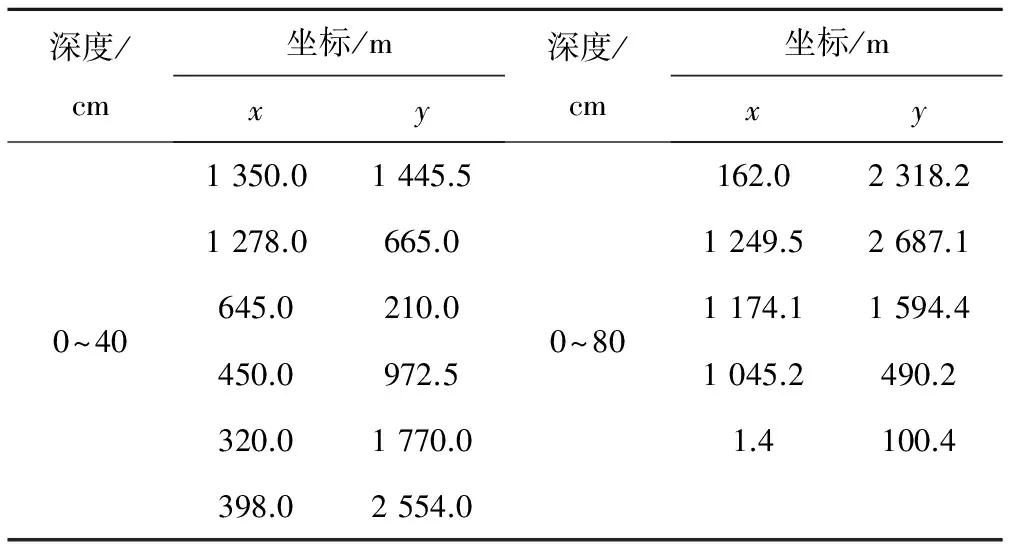
表4 不同深度合理采样点坐标统计Tab.4 Statistics of reasonable sampling point coordinates at different depths

图4 土壤有效最大含水量的空间分布(单位：%)Fig.4 Spatial distribution of soil available maximum water content

2.3 误差分析

以129个样点插值获得的区域含水量作为实测值，优化布设的采样点插值获得的区域含水量作为估算值，将其对应的土壤含水量平均值进行误差分析。具体分析如表5、表6所示。

表5是0～40 cm土壤平均含水量估算值与实测值的误差分析结果。在0～40 cm深度土壤含水量的误差值在1.56%～8.95%范围内变化，均在10%的采样误差范围内，说明0～40 cm深度的6个固定监测点满足采样精度，能够代表区域的土壤含水量。

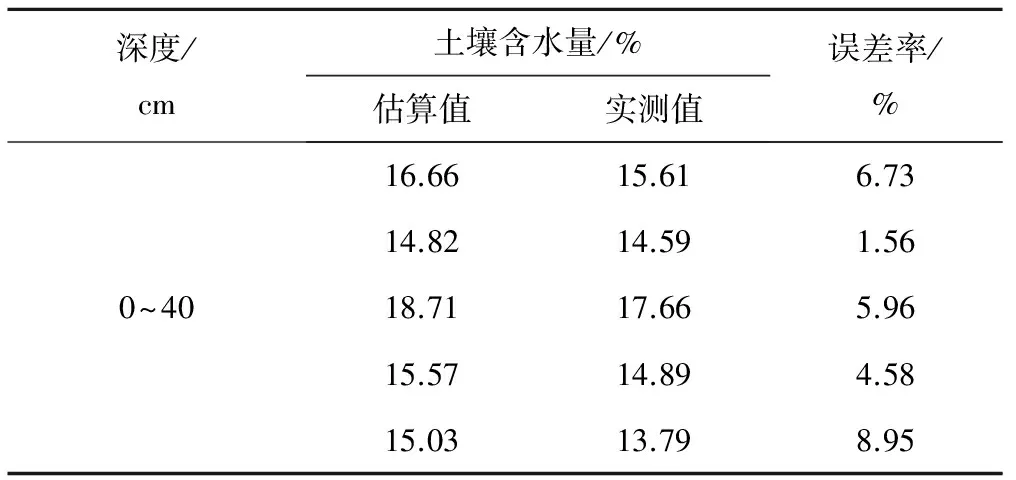
表5 0～40 cm土壤含水量误差分析Tab.5 Analysis of soil water content error at 0～40 cm depth

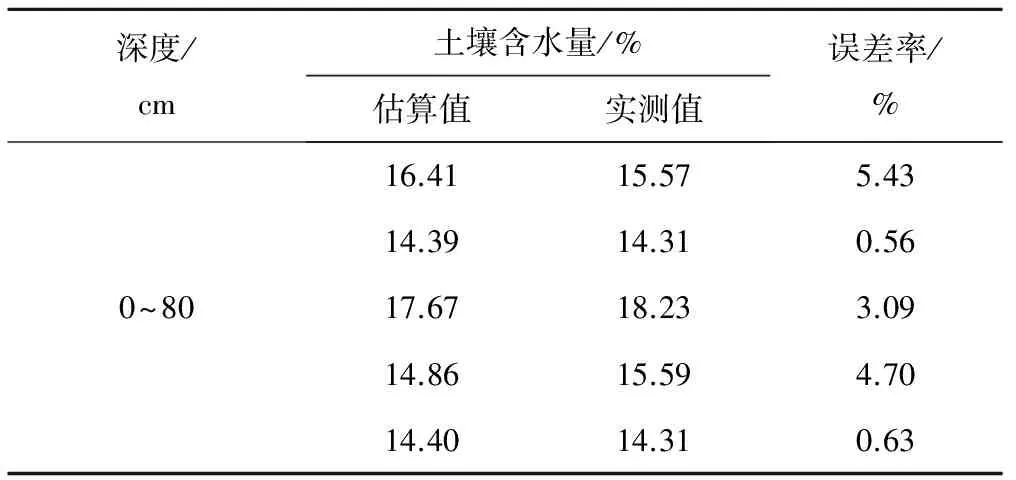
表6 0～80 cm土壤含水量误差分析Tab.6 Analysis of soil water content error at 0～80 cm depth

表6是0～80 cm土壤平均含水量估算值与实测值的误差分析结果。在0～80 cm深度土壤含水量的误差值在0.56%～5.43%范围内变化，均在10%的采样误差范围内，说明0～80 cm深度的5个固定监测点满足采样精度，能够代表区域的土壤含水量。

3 结 语

(1)试验区土壤有效最大含水量在0～40、 0～80 cm深度的变异程度均表现为中等程度，0～40、0～80 cm的土壤有效最大含水量的空间分布情况基本一致，在西南-西北方向的土壤有效最大含水量较大，其他地区较小；且0～40 cm的变化较0～80 cm大。

(2)0～40 cm的土壤有效最大含水量具有中等程度的空间相关性，0～80 cm的土壤有效最大含水量具有较强的空间相关性，相关域分别是780、1 104 m，选择的理论模型均为指数模型。在置信区间90%，采样误差10%的条件下，0～40与0～80 cm的合理采样数分别是6个、5个，在土壤有效最大含水量等值线图中确定具体坐标。

(3)根据试验区129个样点估算的区域土壤含水量与优化布设的采样点估算的区域含水量进行误差分析，结果表明均满足精度要求，说明土壤有效最大含水量可以代替实测含水量值进行测墒点的优化布设。

□

参考文献：

[1] 申祥民,雷晓云.棉花膜下滴灌条件下农田土壤水分的空间变异性研究[D]. 乌鲁木齐：新疆农业大学,2010.

[2] Brocca L, Morbidelli R, Melone F, et al. Soil Moisture Spatial Variability in Experimental Areas of Central Italy[J].Journal of Hydrology(0022-1694). 2007,333:356-373.

[3] 周世军,雷晓云,李芳松,等. 棉花膜下滴灌田间土壤水分的时空变异规律研究[J].中国农村水利水电,2010,(10):22-24.

[4] Herbst M, Diekkruger B. Modeling the spatial variability of soil moisture in a micro-scale catchment and comparison with field data using geostatistics[J]. Phys. Chem. Earth 2003,28(6-7):239-245.

[5] 李芳松,雷晓云,周世军,等.南疆地区棉花整个生育期内土壤水分空间变异性分析[J].水资源与水工程学报,2010,21(2):63-67.

[6] 龚绍琦, 黄家柱, 李云梅, 等. 太湖梅梁湾水质参数空间变异及合理取样数目研究[J]. 地理与地理信息科学, 2006,22(2): 50-54.

[7] 谢恒星,张振华,刘继龙,等.土壤含水量合理取样数目影响因素的试验研究----以烟台苹果园为例[J].干旱地区农业研究, 2007,25(4):114-118.

[8] 信秀丽,张佳宝,朱安宁.区域土壤水分监测点布设方式探讨[J].灌溉排水学报,2008,27(3):16-19.

[9] 汪羽宁,樊 军,李世清.小麦实时控制灌溉的土壤水分含量探头合理埋设深度研究[J].灌溉排水学报,2009,28(5):10-12.

[10] Junior V V, Carvalho. Spatial variability of soil water content and mechanical resistance of Bra Zilian ferralsol[J].Soil and Tillage Research,2006,85 (1-2):166-177．

[11] Ferreyra R A,Apeztegufa H P,Sereno R. Reduction of soil water spatial sampling density using scaled semivariograms and simulated annealing[J].Geodema,2002,110(3-4),265-289.

[12] 申祥民,雷晓云,陈大春,等.不同布点方式的膜下滴灌棉田土壤水分的空间变异研究[J].新疆农业大学学报,2010,33(4):363-368.

[13] Lydia Mumbi CHABALA，Augustine MULOLWA，Obed LUNGU. Application of Ordinary Kriging in Mapping Soil Organic Carbon in Zambia[J].Pedosphere,2017,27(2):338-343.

[14] Wilson D J,Western A W, Rodger B Grayson, et al. Spatial distribution of soil moisture over 6 and 30 cm depth, Mahurangi river catchment, New Zealand[J]. Journal of Hydrology, 2003,276(1-4):254-274.

[15] N.V.Prasolova. Spatial-temporal variability of soil moisture,nitrogen availability indices and other chemical properties in hoop pine (Araucaria cunninghamii) plantations of subtropical Australia[J].Forest Ecology and Management, 2000,136(1-3):1-10.

[16] 李 彦,郑国玉,雷晓云.滴灌棉田灌溉单元内土壤墒情监测点的采样效率研究[J].灌溉排水学报.2014,33(2):90-93.

[17] 张继光,陈洪松,苏以荣,等. 喀斯特地区典型峰丛洼地表层土壤水分空间变异及合理取样数研究 [J]. 水土保持学报, 2006,20(2):114-117.

[18] 杨贵羽,陈亚新. 土壤水分盐分空间变异性与合理采样数研究[J].干旱地区农业研究, 2002,20(4):64-66.

[19] 吴宏平,王树仿,缴锡云. 膜下滴灌墒情监测点布设方案研究[J].水利与建筑工程学报,2015,13(2):144-147.

[20] 孙 凯,王一鸣,杨绍辉.墒情监测取样方法的研究[J].农业工程学报,2004,20(4):74-78.

[21] 陈 坤,雷晓云,李 彦,等.加工番茄膜下滴灌墒情监测点的数目研究[J].节水灌溉，2012,(1)：4-7.

[22] 杨风亮,缴锡云,刘一休,等.棉花膜下滴灌墒情监测点的定位[J].灌溉排水学报,2010,29(3):29-31.

[23] 李芳松,雷晓云,周世军,等.膜下滴灌棉田墒情监测点的横向定位研究[J].节水灌溉,2011,(3):4-6.

[24] Phene C J, Howell T A. Soil sensor control of high-frequency irrigation systems[J]. Transaction of the ASAE, 1984,27(2):102-104.

[25] Stegman E C. Irrigation Water Management[M].Chicago, Illinois, USA :American Society of Agricultural Engineers, 1982:763-816.

[26] Haman D Z,Ross Phil, Tacker D S. Critical management issues for SDI systems in North Carolina[J].North Carolina Cooperative Extension Service,2008,(6):45-56.

[27] 申孝军,孙景生,张寄阳,等.滴灌棉田土壤水分测点最优布设研究[J].干旱地区农业研究,2012,30(3):90-95.

[28] 刘国水,刘 钰,许 迪,等.农田不同尺度蒸散量的尺度效应与气象因子的关系[J].水利学报.2011,42(3):284-289.

[29] 关作正,石 岚,徐丽娜.黄河流域托万区间SWAT模型土壤属性数据库的建立[J].内蒙古水利.2009,(4):5-7.

[30] Cochran W G. Sampling Techniques[M]. Third Edition. New York: John Wiley and Sons, Inc., 1977.

[31] 陈 坤,雷晓云.自动化膜下滴灌加工番茄墒情特征分析及墒情预报模型研究[D]. 乌鲁木齐：新疆农业大学,2012.

[32] 杨诗秀,雷志栋,吴婉如,等.农田尺度土壤水分的监测[J].水科学进展.1996,7(1):14-19.