霞浦海堤工程对福宁湾潮流泥沙的影响分析

吕 江 华

(河海大学海洋学院，南京 210098)

0 引 言

海洋水利工程的建设在一定程度上会对周围海域的水文生态环境产生影响[1]，并给生态环境和原有港口航道造成不同程度的影响[2-5]，因此分析工程建设对工程海域的水文环境影响分析具有重要意义。海堤工程是海岸的一个重要防护工程，避免海浪等一些自然现象对沿海人民的工作和生活产生危害[6]，而海堤工程的建设会改变原本岸线形状，改变原有海洋环境，因此分析海堤工程建设对海域的环境影响的数值模拟具有重要意义[7]。影响分析主要涉及潮流和泥沙，潮流与泥沙的数值模拟起步于20世纪60年代，大体经过从一维到三维的发展[8]。由于科技的进步，90年代三维模型得到广泛应用，三维模型具有应用范围广、模拟精度高等优点，能更好地模拟研究区域的实际情况。在以往影响评估的相关研究中，采用的模型有MIKE、ROMS、FVCOM等[9]，其中FVCOM相比较其他几种模型而言，采用水平三角形网格，在近岸复杂地形模拟中更加准确。

霞浦县小皓村位于三沙镇与霞浦县之间，本项目位于东海海域西南方向福宁湾海域(图1)，海堤全长431 m，顶高程为6.00 m，后方回填形成陆域2.452 2 万m2，形成的陆域布置为新农村建设，滩涂绿地和陆域道路。本研究运用FVCOM海洋数值模式建立了福宁湾三维潮流数学模型，通过实测水位、流速、流向和含沙量对模型进行验证，模拟计算结果与实测资料吻合较好，验证后的模型可用于预测霞浦海堤工程对工程海域水文环境的影响。

图1 项目位置Fig.1 The project location

1 模型的建立

1.1 FVCOM模式简介

本文所应用的FVCOM(Finite Volume Coast and Ocean Model)数值模式是由美国马萨诸大学与伍兹霍尔海洋研究所联合开发的三维海洋模式[10]，该模型垂向采用σ坐标，能够精确模拟不规则的海底地形水深变化，水平方向采用非结构的三角网格，采用有限体积的方法，通过积分的方式计算重叠水平三角形控制体的通量来解控制方程。这种有限体积方法很好地将有限元方法处理海湾岸边界复杂曲折的优点和有限差分方法简单的离散结构、高效的计算效率结合起来，对于近岸河口等具有复杂地形的区域可以更好地保证质量、动量、盐度和热量的守恒性。FVCOM分别与POM以及ECOM-si在理想化实验和近岸河口区域模拟中的对比结果[11]说明，岸线拟合的程度以及数值方法的选择在边界较为复杂的近岸河口海域的潮流数值模拟中具有重要的作用,这也正是FVCOM的优势所在[12]。

1.2 模型建立

本模型计算范围为整个福宁湾海域，图2为模型计算区域和水深布置图。计算区域划分为高质量、非结构的三角形网格，工程海域网格进行加密处理。计算时间步长为10 s，垂向 坐标分均匀6层，计算区域三角网格节点数为73 593 个，网格单元数为143 948 个，最小网格间距为5 m。图3为工程前后工程海域网格和水深分布图。温盐初始场采用常值，模型初始水位是NOAA发布的ETOPO1地形高程数据所提供，模式从静止状态启动[13]。开边界自西南起七尺门到东北三沙角连线，采用水位强迫作为开边界，本模型的开边界(水边界)水位是通过TMD(Tide Model Driver)同化卫星高度计资料得到各主要分潮调和常数后再预报得到的，考虑了M2、S2、K2、N2、O1、K1、P1和Q1这8个主要分潮。

1.3 模型验证

模型验证数据采用2013年6月霞浦县三沙小皓临时站工程水文泥沙测验分析报告[14]。该观测进行3个大潮海流连续站(C1、C2、C3)各28 h的海流观测，以及一个15 d的水位连续观测站(T1)。观测站位的详细信息见图4和表1。

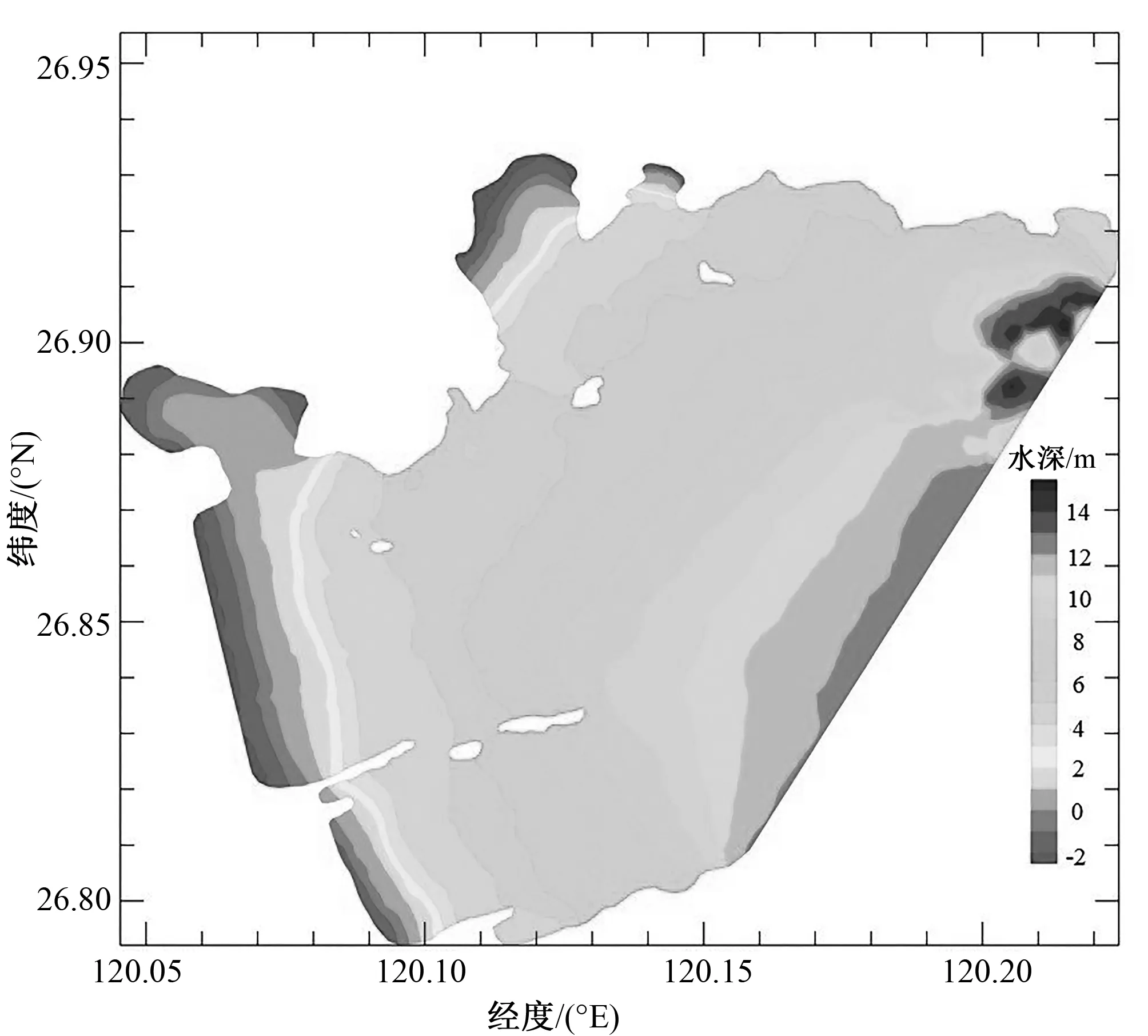
图2 模型计算区域及水深布置Fig.2 Calculation area and depth

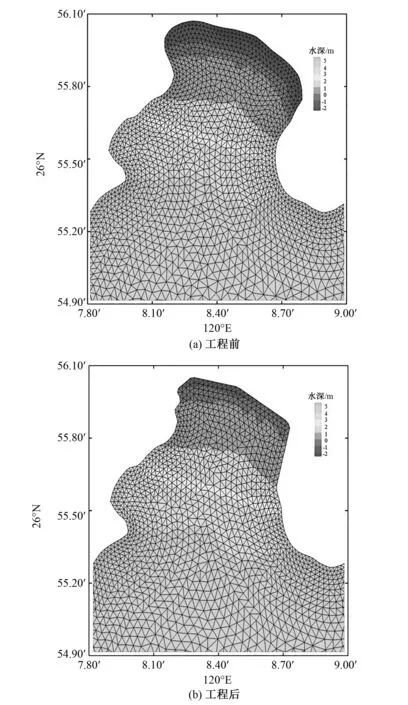
图3 工程前后工程海域网格和水深分布图Fig.3 The grids and depth of the calculation area before and after the project

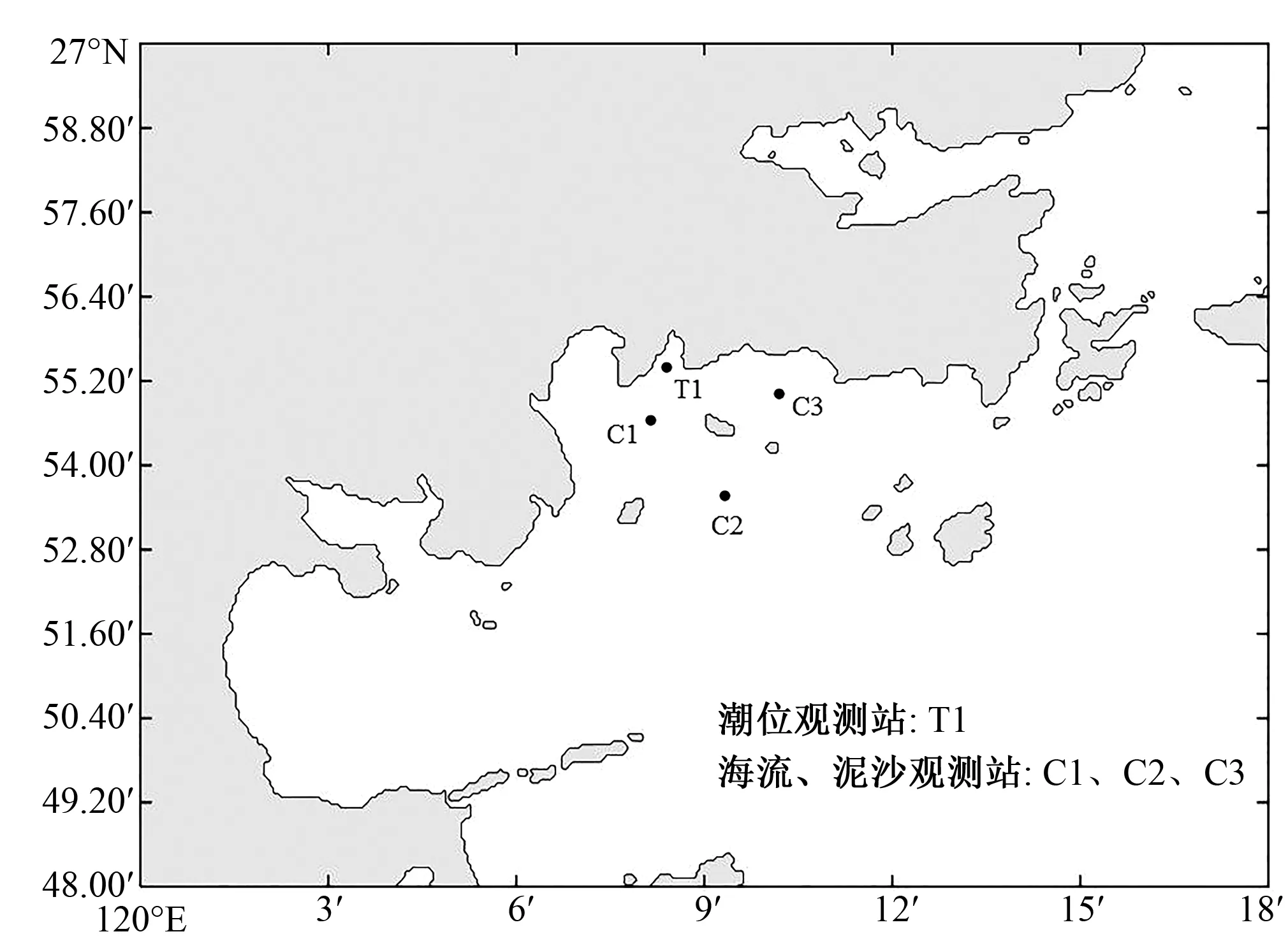
图4 模型验证观测站位图Fig.4 The observation stations

项目站号北纬东经潮位T126°55′32．91″120°8′40．71″C126°55′24．98″120°8′26．28″海流C226°54′4．51″120°8′22．72″C326°54′58．58″120°9′43．00″

T1站水位以及C1、C2、C3站海流流速和流向观测值与计算值时间过程对比如图5～图7所示(以表层为例)。从水位过程对比曲线看出，水位计算值与观测值吻合良好，潮涨历时与落潮历时基本一致，潮位最大误差0.49 m，平均绝对误差0.023 m，相对误差为0.47%。从流速对比图可以看出3个观测站中最大平均绝对误差为0.021 m/s，最大相对误差为9.88%，均小于10%，涨落潮时最大流速值以及出现时间点计算值与观测值吻合良好。从流向模型对比图看出平均流向偏差为1°～8°，流向相对流速大小而言模拟结果符合校核，高低潮及转流时间也基本一致(表2为各站流速、流向偏差表)。

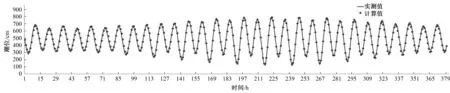
图5 潮位计算值和实测值验证图Fig.5 Verification of the calculated values and the observed of the tide

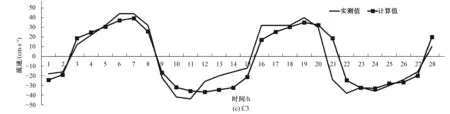
图6 流速计算值和实测值验证图Fig.6 Verification of the calculated values and the observed of the flow velocity

图7 流向计算值和实测值比较图Fig.7 Verification of the calculated values and the observed of the flow direction

站点T1潮位/mC1流速/(m·s-1)流向/(°)C2流速/(m·s-1)流向/(°)C3流速/(m·s-1)流向/(°)平均绝对误差0．0230．0141．2100．0196．0900．0217．070相对误差/%0．479．880．608．603．127．443．43

通过潮位和潮流的对比验证可以看出，模拟结果与实测过程吻合较好，满足规范要求[15]，所建模型采用的物理参数和计算参数基本合理，计算方法可靠，能够较为准确地刻画霞浦海堤附近海域水动力情况，可以继续利用此模型模拟工程区附近海域潮流场变化。

2 工程对海域潮流场的影响分析

2.1 工程前后流场变化分析

为分析霞浦海堤工程建设对周边海域潮流场的影响，依据数值模拟结果分别给出福宁湾大范围和网格加密区域中工程前后大、小潮涨落潮流场图(以大潮为例见图8～图10)。

由图8可见，工程实施前，该海域流速普遍较低，涨急时刻形成了比较明显的沿岸流，最大流速在笊篱山南部海域达到0.84 m/s，湾内流速基本在0.28 m/s以下。同时由于该海域浅海滩涂面积较大，在涨落潮阶段有大片潮滩露出。总体而言工程建设前涨急流速大于落急流速，沿岸流的流场特征明显。

通过工程实施前后流场对比结果图可见，工程实施后对工程海域湾内小海域流场有较大的影响，对外围区域影响较小。海堤附近潮流流向发生调整，新流向与新岸线走向基本一致，对大区域流场的流向也无显著影响。

2.2 工程前后流速对比点流速变化

为了定量分析工程实施对工程海域水动力的影响，在海堤外侧布设了5个流速比较点。图11为工程海域工程前后流速对比点分布图。

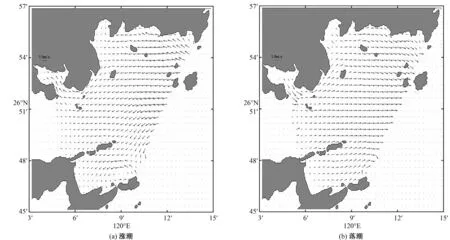
图8 计算区域涨潮流场图和落潮流场图Fig. 8 The flow field of the calculation area during high tide and ebb

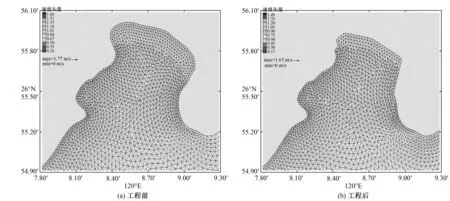
图9 工程前后工程附近海域涨潮流场对比Fig. 9 Comparison of the flow field in the project seas during high tide before and after the project

图10 工程前后工程附近海域落潮流场对比Fig.10 Comparison of the flow field in the project seas during ebb before and after the project

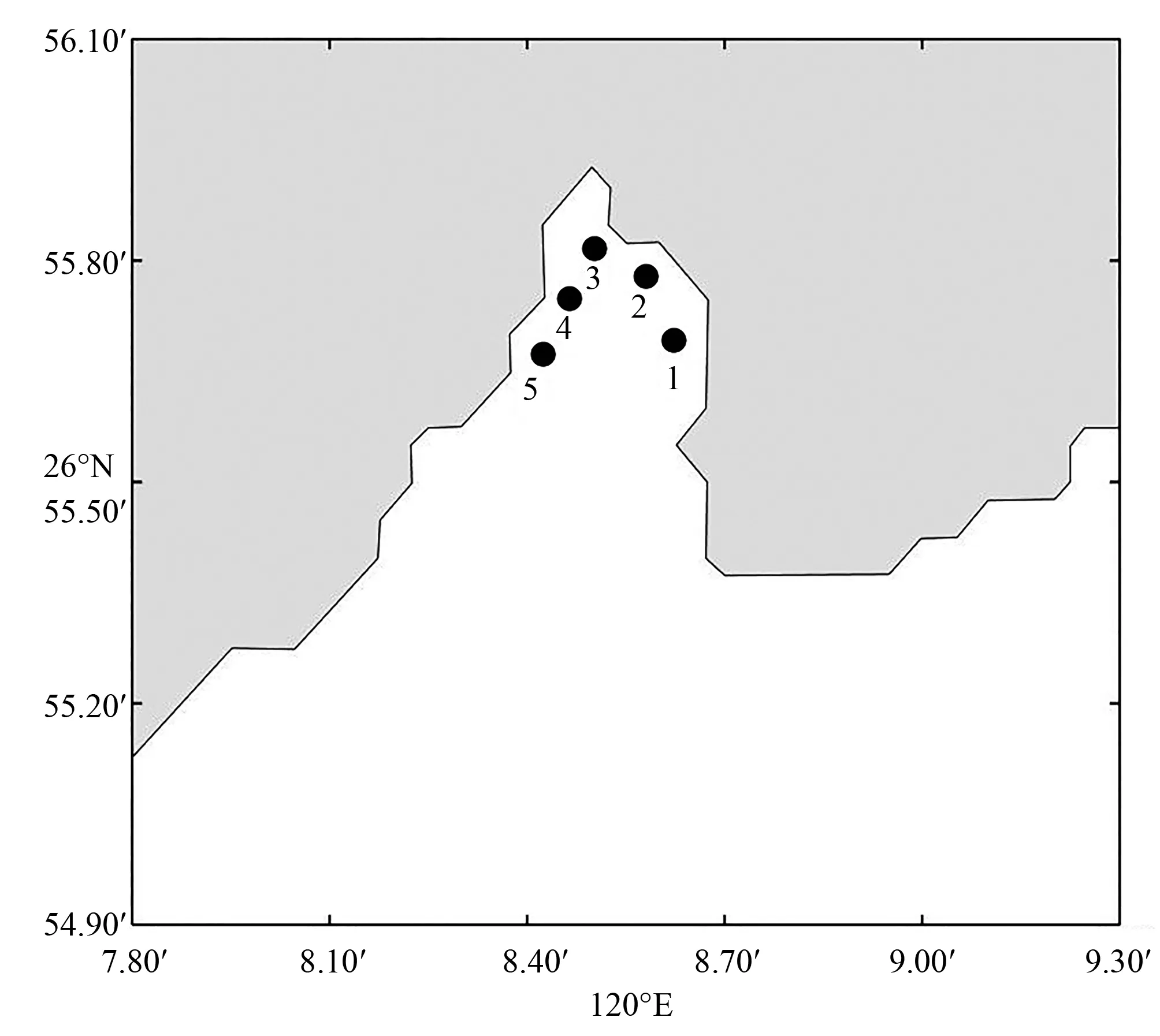
图11 流速比较点分布Fig.11 Comparison points of the flow velocity

根据模型计算的工程前后大小潮期间(以大潮为例)涨落潮过程中的各流速比较点上的平均流速、流向和最大流速、流向比较数据可知，工程的实施对工程海域的流速带来局部影响。所选的5个点中，涨潮时3号和5号点工程后流速变化较大，最大增幅可达0.024 m/s，其他3个点的流速变化较小，变化的幅度不超过0.01 m/s；在落潮时只有2号点的流速变化较大，流速增幅为0.025 m/s，其他4个点的流速变化均比较小，流速变幅不超过0.01 m/s。此外，各点流向均与工程前发生改变，由于岸线改变，在海堤附近海域流向发生逆时针偏转，新流向大致保持与岸线平行。

总体来看，霞浦海堤工程建设只对以湾内500 m海域的水流产生影响。主要变化区域集中在海堤工程沿岸及拐角处，涨潮时刻在海堤拐角处南侧海域和工程西端流速变化相对较大，落潮时只在西侧拐角处流速变化较大，工程海域流向与工程前发生改变，由于岸线改变，在海堤附近海域流向发生逆时针偏转，新流向大致保持与岸线平行，而距离工程较远的外围海域流速流向变化均不明显。

3 工程附近海域冲淤变化分析

福宁湾海域悬浮泥沙观测包括大、小潮两次测验，布设3个水文泥沙观测站，站位布设位置与海流观测站位一致(图4)，该海域海水含沙浓度较低，实测最高含沙量为0.139 6 kg/m3，大潮总平均含沙量为0.041 1 kg/m3水域表现为自表层向底层明显递增的变化特性。霞浦海堤工程建设后，在一定程度上改变了工程海域的水动力环境，使海域潮流场的动态平衡格局发生改变，使该海域出现冲淤变化。

工程区海域年回淤淤强公式采用半经验半理论公式：

(1)

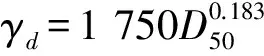
含沙量计算按刘家驹提出的风浪和潮流综合作用的挟沙能力公式：

(2)

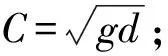
图12 含沙量计算值和实测值验证图Fig.12 Verification of the calculated values and the observed of the Sediment concentration

选取C1、C2和C3三个测站的含沙量进行模式验证分析(以大潮垂向平均为例)。通过将计算值与实测值相比较，整体趋势基本一致，误差较小(图12)。总体看来，所用模型中物理参数以及计算相关参数的选取较合理，计算方法有效，能够很好地模拟工程海域的泥沙运动。

霞浦海堤的建设改变了岸界，进而改变了工程海域的水动力环境，从而使得工程海域冲淤环境发生了变化，根据工程前后的水动力数值模拟结果，计算出工程附近海域年冲淤强度分布(图13)，由图13可知，工程的建设对工程附近海域泥沙冲淤环境的影响比较微弱，影响主要集中在新岸线拐角处海域，结合该海域流场变化分布可知，泥沙浓度与流场之间存在较好的对应关系，流速增大的位置呈冲刷状态，主要发生在海堤南侧海域，最大冲刷厚度为0.012 m/a，流速减小的位置呈淤积状态，主要发生在海堤新岸线拐角处，但其年淤积厚度均小于0.004 m/a。海堤工程对周边海域有一定影响作用，部分区域存在轻微冲刷以及轻微淤积，总体影响范围较小。

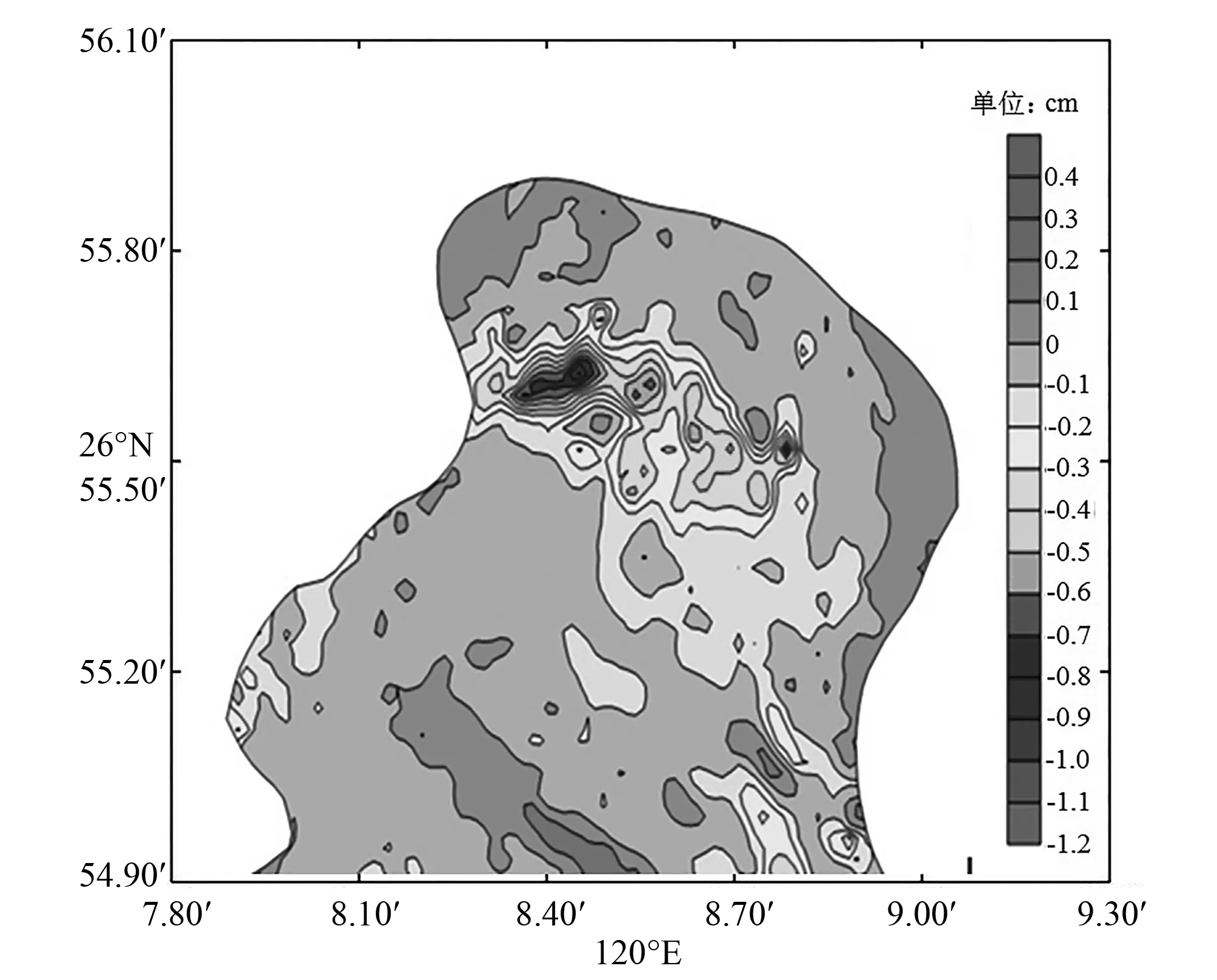
图13 工程建设后年淤积厚度(正值为淤积，负值为冲刷)Fig.13 Siltation intensity after the project (The positive value is siltation, the negative value is scour)

4 结 语

基于非结构网格、干-湿判别技术和有限体积法的FVCOM海洋数值模式，建立了福宁湾海域的三维潮流场数学模型，通过实测潮位、流速、流向和含沙量对模型进行了验证，模拟值与实测资料吻合较好，用验证后的模型预测霞浦海堤工程对该海域潮流场和冲淤环境的影响，得到下列主要结论。

(1)福宁湾海域属于正规半日潮型的强潮海域，潮差较大。工程建设前各站位因地形的影响，涨落潮表现不一致，整体体现涨潮流速大于落潮流速，小潮期间因涨潮影响减落。港湾内观测海域的潮流系潮沟和岸形制约，沿着岸线方向涨落潮。

(2)工程实施前，涨潮总体流向为外海向陇头小皓村海岸线，落潮反之。工程实施后，海堤附近潮流流向与工程前对比发生调整，由于岸线改变，在海堤附近海域流向发生逆时针偏转，新流向与新岸线走向基本一致。

(3)工程的实施对工程海域的流速带来局部影响。所选的5个流速比较点中，涨潮时3号点和5号点即海堤东西两侧拐角处工程后流速变化较大，最大增速为0.024 m/s，其他3个点的流速变化较小，变化的幅度不超过0.01 m/s；在落潮时只有2号点的流速变化较大，流速变幅达到0.025 m/s，其他4个点的流速变化均比较小，流速变幅不超过0.01 m/s。工程的实施对外围海域流场无显著影响。

(4)工程建设后，流速增大的位置呈冲刷状态，主要发生在海堤南侧海域，最大冲刷厚度为0.012 m/a，流速减小的位置呈淤积状态，主要发生在海堤新岸线拐角处，但其年淤积厚度均小于0.004 m/a。海堤工程对周边海域有一定影响作用，部分区域存在轻微冲刷以及轻微淤积，总体影响范围较小。

□

参考文献：

[1] 具杏祥,苏学灵. 水利工程建设对水生态环境系统影响分析[J]. 中国农村水利水电, 2008,(7):8-11.

[2] 曹宇峰,林春梅,余麒祥,等. 简谈围填海工程对海洋生态环境的影响[J].海洋开发与管理,2015,32(6):85-88.

[3] 谢 挺,胡益峰,郭鹏军. 舟山海域围填海工程对海洋环境的影响及防治措施与对策[J]. 海洋环境科学,2009,28(s1):105-108.

[4] Zhang W, Liu R, Qian W, et al. Influence of large-scale coastal engineering on hydrodynamics and sediment transport[J]. Journal of Waterway & Harbor, 2014.

[5] Gui F U, Jiufa L I, Dai Z, et al. Study of tidal flow numerical simulation on the reclamation project of nanhuizui beach[J]. Transactions of Oceanology & Limnology, 2007.

[6] 刘 宁,孙东亚,黄世昌,等. 风暴潮灾害防治及海堤工程建设[J]. 中国水利, 2008,(5):9-13.

[7] 蔡 磊, 王燕燕,刘西平,等. 天津某海堤工程对水动力环境影响数值模拟[J]. 港工技术, 2017,54(1):17-22.

[8] 远 航,于定勇. 潮流与泥沙数值模拟回顾及进展[J]. 海洋科学进展, 2004,22(1):97-106.

[9] 郑沛楠,宋 军,张芳苒,等. 常用海洋数值模式简介[J]. 海洋预报,2008,25(4):108-120.

[10] Chen C, Liu H, Beardsley R C. An Unstructured Grid, Finite-Volume, Three-Dimensional, Primitive Equations Ocean Model: Application to Coastal Ocean and Estuaries[J]. Journal of Atmospheric & Oceanic Technology, 2003,20(20):159-186.

[11] Chen C, Huang H, Beardsley R C, et al. A finite volume numerical approach for coastal ocean circulation studies: Comparisons with finite difference models[M]. Journal of Geophysical Research: Oceans (1978-2012), 2007:83-87.

[12] 宋德海,鲍献文, 朱学明.基于FVCOM的钦州湾三维潮流数值模拟[J]. 热带海洋学报,2009,28(2):7-14.

[13] 吴修广, 刘光生, 程文龙. 基于FVCOM的杭州湾三维泥沙数值模拟[J]. 水利水运工程学报, 2011(4):86-96.

[14] 福建中海检测技术有限公司. 霞浦县三沙小皓二级渔港工程水文泥沙测验分析报告[Z]. 2013.

[15] JTS/T 231-2-2010，海岸与河口潮流泥沙模拟技术规程[S].