基于复合形遗传算法的新安江模型参数优化率定研究
周瑜佳,陈一帆,淡娇娇,刘立军
(浙江省水利河口研究院 浙江省水利防灾减灾重点实验室,杭州 310020)
1 概 述
洪水预报是一项直接服务于国民经济建设不可或缺的重要工作,能帮助人类有效防御洪水、减少洪灾损失、更好地控制和利用水资源,是一项重要的防洪减灾非工程措施[1]。新安江模型被广泛应用于南方湿润半湿润地区的径流计算及洪水预报中,其参数大多具有明确的物理意义,对模型计算结果的合理性和准确性影响较大。
随着计算机技术的发展和广泛应用,基于计算机算法程序设计的参数自动率定方法成为重要工具,有效避免了参数率定过程中的主观性与随机性。自20世纪70年代新安江模型提出以来,模拟退火法、SCE-UA、粒子群法、遗传算法(GA)等[2-5]自动优化率定方法相继应用于新安江模型参数自动优化率定,其中遗传算法因具有简单通用、鲁棒性强、全局寻优等特点,常用于解决非解析式的目标函数和约束问题,成为水文学者研究探索参数率定的重要手段[6]。但是,遗传算法在寻优空间较大时计算效率低且易陷入局部最优,为此,研究者们试图通过混合法策略达到方法之间的取长补短。李水艳[7]针对传统遗传算法存在的不足,提出了一种改进遗传算法用于解决三水源新安江模型中的参数率定问题;孟新华等[8]结合新安江模型参数的特点,将模拟退火算法与传统遗传算法相结合的混合算法运用于新安江模型参数优选中;郭靖等[9]运用TOPSIS法结合遗传算法,研究其在水文模型多目标参数自动优选中的可行性。
本文将遗传算法与复合形法相结合,构建了一种复合形遗传算法,并采用分层率定思想对浙江省下回头水文站以上集水流域进行了新安江模型参数优化率定,取得了良好效果。
2 复合形遗传算法
2.1 复合形法
复合形法(Complex Method)是一种求解非线性规划约束问题的有效解决方法[10]。方法的基本思路:在寻优空间选取K个顶点作为初始复合形的顶点,计算、比较各顶点目标函数值,函数值最大者作为最坏点去掉,并通过映射计算得到替代新顶点,构成新的复合形。重复以上过程,直到收敛,取最后一个复合形中目标函数值最小的顶点作为近似最优解[11]。复合形法计算步骤:①构造初始复合形;②计算各顶点的目标函数值f(X(j)),j=1,2,…,K。选出最好点X(L)与最坏点X(H);③计算除最坏点外其余各顶点之形心X0;④计算映射点X(R)。
X(R)=X0+α(X0-X(H))
(1)
式中:α为映射系数,一般取α=1.3。
检查X(R)是否在可行域内,若X(R)为不可行点,将映射系数减半后再按式(1)计算映射点,直至X(R)进入可行域内。
⑤构造新复合形。计算映射点的目标函数值,并与最坏点的目标函数值进行比较,可能出现两种结果:
(1)映射点优于最坏点,即:
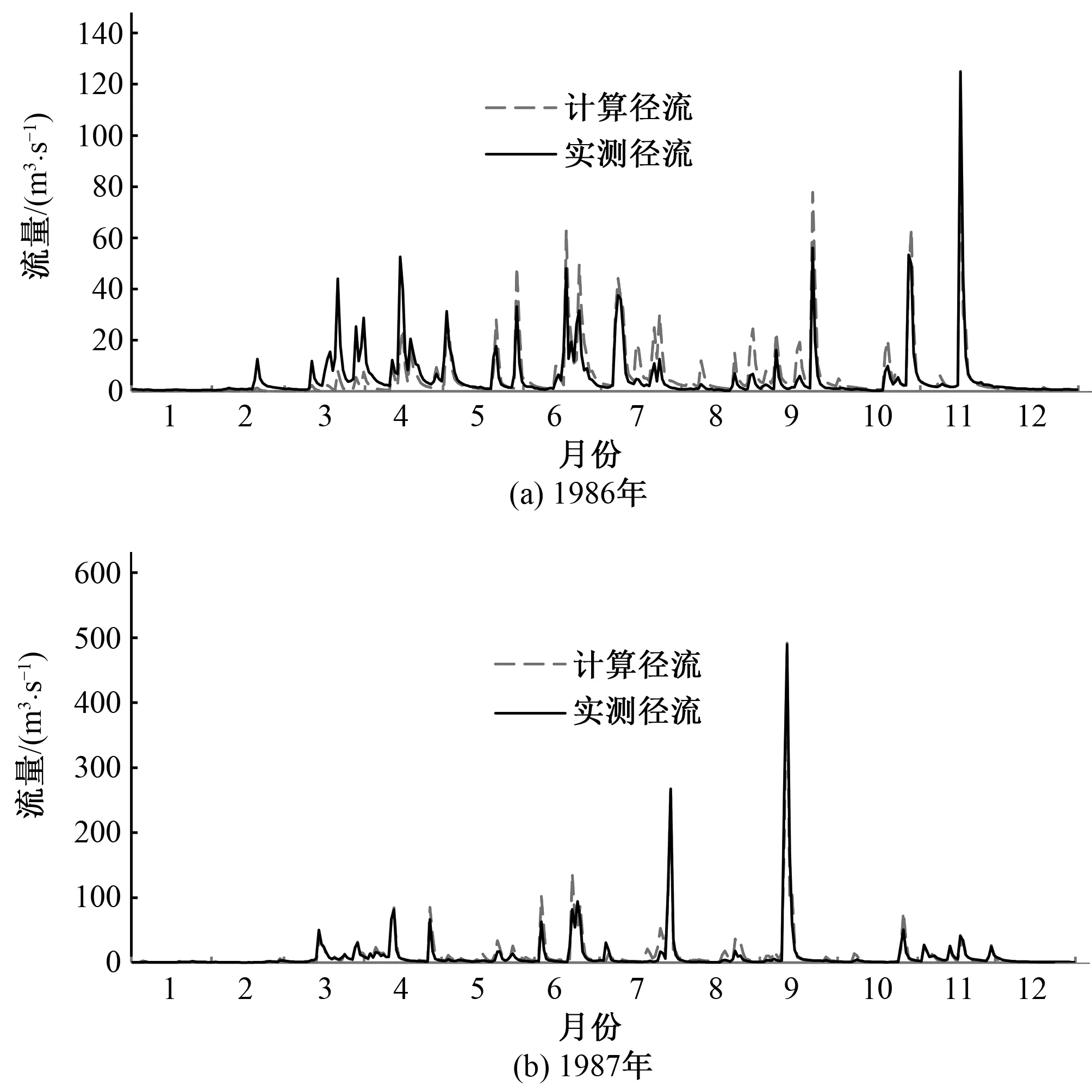
f(X(R)) (2) 在这种情况下,则用X(R)替代X(H),构成新的复合形。 (2)映射点次于最坏点,即: f(X(R))>f(X(H)) (3) 这种结果可能是因为映射点过远,可通过减半映射系数α把映射点拉近,如果f(X(R)) ⑥迭代终止判别。每一个新复合形构成之后,进行终止条件判别,常用的迭代终止条件如下: (1)各顶点与最好点函数值之差的均方根小于限值,即: (4) (2)各顶点与最好点函数值之差的平方和小于限值,即: (5) (3)各顶点与最好点函数值之差的绝对值之和小于限值,即: (6) 如果不满足收敛条件,则返回步骤②继续进行计算,如果满足收敛条件,则最后一次复合形的最好点X(L)和函数值f(X(L))作为最优解,寻优结束。复合形寻优流程见图1。 图1 复合形法寻优流程图Fig.1 Optimization process of complex method 遗传算法具有良好的全局寻优特征,但有可能落入局部最优及收敛不成熟等问题;复合形法具有良好的局部寻优特征,但是复合形法在迭代计算中可能发生失败,尤其是在复杂的优化问题中,且结果受初始复合形的影响较大[12,13]。针对两种算法各自的优势及存在的问题,得出以下算法结合的思路:先利用遗传算法进行全局寻优,得到较优解空间,并在较优解空间内构造初始复合形,再通过复合形法在此解空间中进行二次寻优,最终得到全局最优解,复合形遗传算法流程见图2。本文采用二进制编码进行遗传算法中染色体编译,计算开始先进行种群初始化,包括设置种群最大世代数Tmax、种群规模、个体间的交叉率、变异率及初始化个体等。问题的目标函数值为实测流量与模拟流量之间的偏差,约束条件为各参数合理的取值范围。 图2 复合形遗传算法流程图Fig.2 Process of complex genetic algorithm 三水源新安江模型通过降水量P、实测蒸散发能力EM的输入,预报预测流域出口断面的径流量Q[14]。模型结构和模型参数物理意义见图3和表1。 图3 新安江模型结构流程图Fig.3 Structural process of Xinanjiang model 分类参数物理意义常用取值范围模型主体参数WM/mm流域平均张力水容量80~200WUM/mm上层张力水容量5~20WLM/mm下层张力水容量60~90WDM/mm深层张力水容量-K蒸散发折算系数0.1~1.0C深层蒸散发系数0.1~0.2B张力水蓄水容量曲线方次0.2~0.3IMP不透水面积占全流域面积比值0.001~0.02SM/mm表层土自由水容量5~45EX表层土自由水蓄水容量曲线方次1.0~1.5KI表层土自由水对壤中流的出流系数0 新安江模型分为4个耦合的计算过程,即蒸发→产流→分水源→汇流,参数相应的分为4类,且不同类参数之间基本独立。为了参数优化率定的准确性及合理性,采用分层率定法控制每层的率定指标,如下[15]: (1)蒸散发和产流。蒸散发和产流层的参数有K、C、B、IMP、WUM、WLM、WDM。这些参数决定产流总量,控制着降雨、蒸发及产流间的水量平衡。在降雨已知的情况下,只要以水量平衡方程为目标,对参数进行优化即可。若有实测的径流量资料,我们只需使多年产流总量的误差最小,公式如下: (7) 式中:Qobs(i)为实测流量,m3/s;Qsim(i)为计算流量,m3/s;n为资料系列长度。 (2)分水源和汇流。分水源和汇流层的参数有SM、EX、KI、KG、CI、CG、NK、NT、KE、XE。这些参数主要决定了流量过程,影响优化结果中Nash-Sutcliffe效率系数。其中地面径流影响高水过程,主要作用参数为SM、EX、KI、KG、NK、NT。地下径流影响低水过程,主要作用参数为KI、KG、CG,SM也有一定的影响。 首先,本文选用目标函数FLOG对参数SM、KI、KG、CG、NK、NT进行率定,由于EX最优值稳定在1~1.5,不参加率定,目标函数如下式: (8) 其次,由于SM对高水部分比较敏感,选用目标函数FABS对SM进行优化,目标函数如下式: (9) 最后,由于NK、NT对Nash-Sutcliffe效率系数有影响,我们选用目标函数FNASH对参数NK、NT进行微调,目标函数如下式: (10) 对新安江模型进行分层优化率定能够使各参数的取值更符合其物理意义,能够更有利于减小总径流量误差,使流量过程拟合效果更好。在对模型的参数进行分层以后,再用复合形遗传算法进行寻优,复合形遗传算法各参数的取值见表2。 朱溪是永安溪在仙居城区以下的主要支流,发源于仙居县东南部的下坑,自南往北流经方山村、梅岙、下回头、大战等地,在后林村附近注入永安溪干流,河长49.2 km,流域面积379.3 km2。下回头水文站位于朱溪下游,集水面积241 km2。朱溪流域的地形分布以中低山区为主,河道坡降大、水流急,洪水过程陡涨陡落。流域山地植被较好,水土流失较少。 表2 遗传算法复合形法参数取值Tab.2 parameter value of genetic algorithm and complex method 下回头水文测站位于仙居大战乡上马村,1956年设站,测站以上流域内有苗寮、溪上、仙居梅岙、大洪4个雨量站。为了保障资料具有较好的一致性,选取下垫面变化较小的年份进行模型试验,以1972-1981年共计10年资料作为参数率定期,以1982-1988年共7年资料作为参数检验期,期间发生过接近50年一遇、20年一遇和10年一遇的较大洪水,资料具有较好的代表性。逐日降水量取自下回头站、苗寮站、溪上站和大洪站,逐日蒸散发取自仙居梅岙站,逐日径流取自下回头水文站。分析所涉及站点的资料均经过浙江省水文局审核整编,资料可靠。 遗传算法进行寻优时,敏感性强的参数给定的范围可适当放大,有利于其寻得最优解空间,但过大会导致算法收敛速度减慢;敏感性弱的参数给定的范围可适当缩小。通过遗传算法寻优,不敏感的参数所得的结果可直接确定为最优解,在复合形法中不再对其进行二次寻优。参数优化率定结果见表3。 表3 复合形遗传算法参数优化率定成果表Tab.3 Optimization results with complex genetic algorithm 采用率定所得参数成果以及流域检验期的降水量、蒸散发和径流数据资料,构建检验期三水源新安江模型进行验证计算。首先调整模型的初始条件参数,使得检验期第一年计算径流过程与实测径流过程较好吻合,再对检验期其他年份进行模拟验证,最后计算得到检验期各年的径流量相对误差和径流过程确定性系数,评定他们是否符合预报标准。验证结果见表4和图4(以确定性系数最低年和确定性系数最高年分别为例)。 表4 下回头站以上流域径流误差表Tab.4 Runoff error of watershed aboveXiahuitou station 图4 1986、1987年径流过程模拟图Fig.4 Runoff process simulation in 1986/1987 由表4可知,将复合形遗传算法优化率定得到的参数应用于下回头站以上流域,计算得到的年径流总量误差控制在10%以内,多年平均计算径流深为1 024.1 mm,与实测多年平均径流深1 037.9 mm比较,绝对误差为13.8 mm,相对误差为1%。根据我国颁布的《水文情报预报规范》,各年模拟的流量过程精度均达到乙级标准及以上。 本文针对遗传算法和复合形法各自的优势和存在的问题,根据“取长补短”原则,将遗传算法与复合形法进行结合,构建了一种适用于线性系统及非线性复杂系统参数优化率定的复合形遗传算法。并将其应用于新安江三水源模型的参数优化率定。通过浙江省朱溪下回头站以上流域的案例分析,检验了复合形遗传算法对新安江三水源模型参数优化率定的可行性,取得了良好效果。 另外,算法结合的方式并不唯一,本文只研究了一种结合方式,后期将根据实际优化问题的需要对算法结合的方式进行研究,使其更适用于解决实际问题。 □ 参考文献: [1] 李隆玲,任金政. 我国洪水灾害现状及区划特征[J]. 中国水利,2014,(7):48-51. [2] 张行南.模糊数学在新安江模型参数自动优选中的应用[J].河海大学学报,1988,(3):128-135. [3] 沈同林,姜铁兵,范文涛.用并行遗传算法率定概念性降雨-径流模型[C]∥中国系统工程学会:2000:6. [4] Hapuarachchi H.A.P.,李致家,王寿辉.SCE-UA方法在新安江模型参数优化中的应用(英文)[J].湖泊科学,2001,(4):304-314. [5] 董洁平,李致家,戴健男.基于SCE-UA算法的新安江模型参数优化及应用[J].河海大学学报,2012,(5):485-490. [6] 武新宇,程春田,赵鸣雁.基于并行遗传算法的新安江模型参数优化率定方法[J].水利学报,2004,(11):85-90. [7] 李水艳.改进遗传算法及其在降雨径流模型中的应用[D]. 南京:河海大学,2006. [8] 孟新华,涂启玉,周年华,等.基于遗传模拟退火算法的新安江模型参数优选[J].水电自动化与大坝监测,2009,(3):64-67. [9] 郭 靖,郭生练,胡安焱,等.基于TOPSIS法的水文模型多目标参数自动优选方法研究[J].水电能源科学,2006,(6):25-29. [10] 王思仁. 复合形法及其应用[J]. 江西水利科技,1995,(2):93-97. [11] 陈 刚,张 林,陈健康,等.复合形法在拱坝结构可靠度分析中的应用[J].水利学报,2003,(2):98-101,106. [12] 李 亮,迟世春,林 皋.基于蚁群算法的复合形法及其在边坡稳定分析中的应用[J].岩土工程学报,2004,(5):691-696. [13] 崔珊珊. 遗传算法的一些改进及其应用[D]. 合肥:中国科学技术大学,2010. [14] 赵人俊. 流域水文模拟: 新安江模型与陕北模型[M]. 北京: 水利电力出版社, 1984. [15] 陈坰烽,张万昌. 基于遗传算法的新安江模型日模拟参数优选研究[J]. 水文,2006,(4):32-38.
2.2 复合形法与遗传算法结合
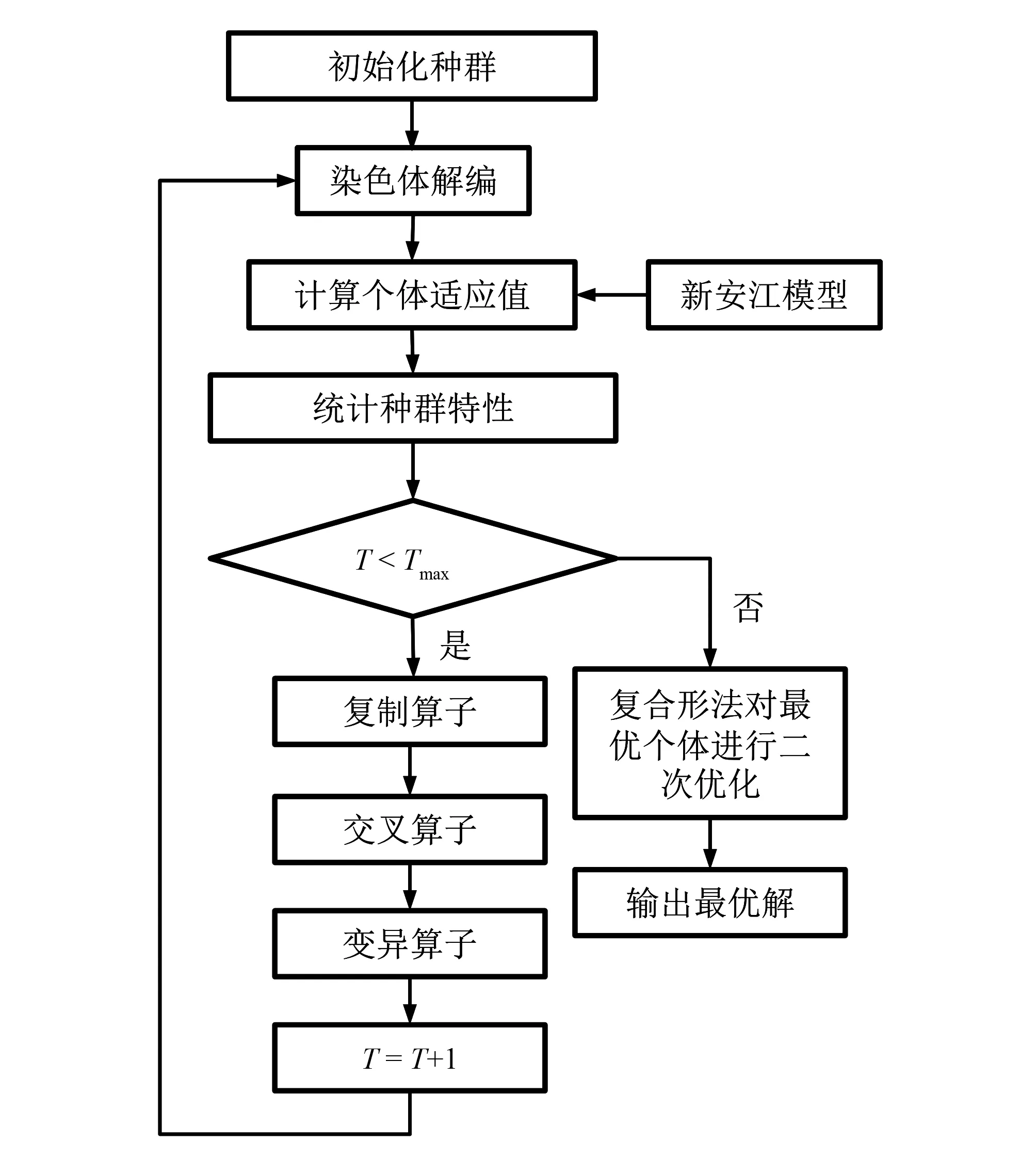
3 复合形遗传算法与新安江模型



4 实例分析
4.1 研究区域与数据资料
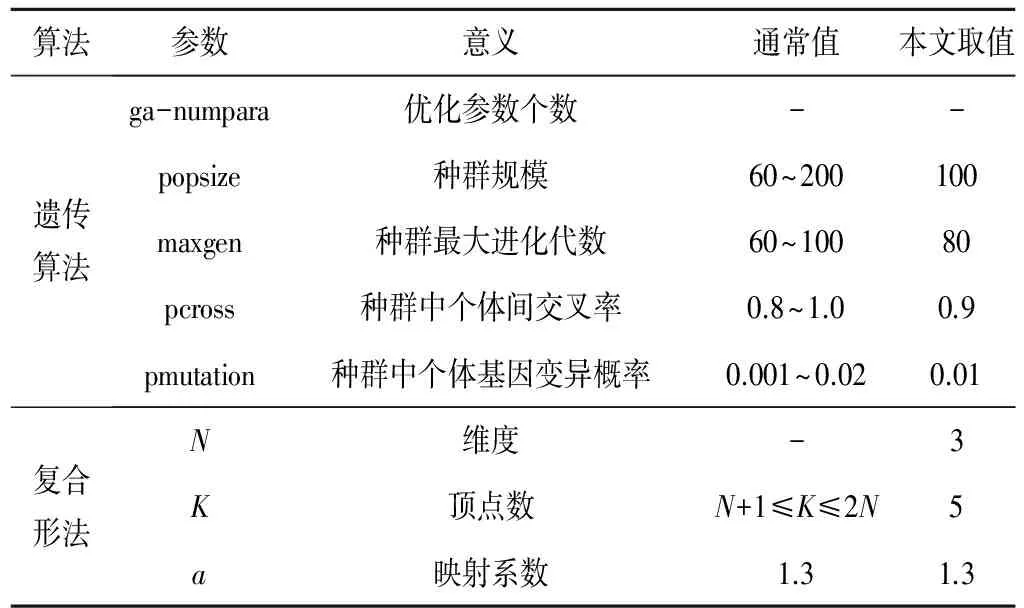
4.2 参数率定结果
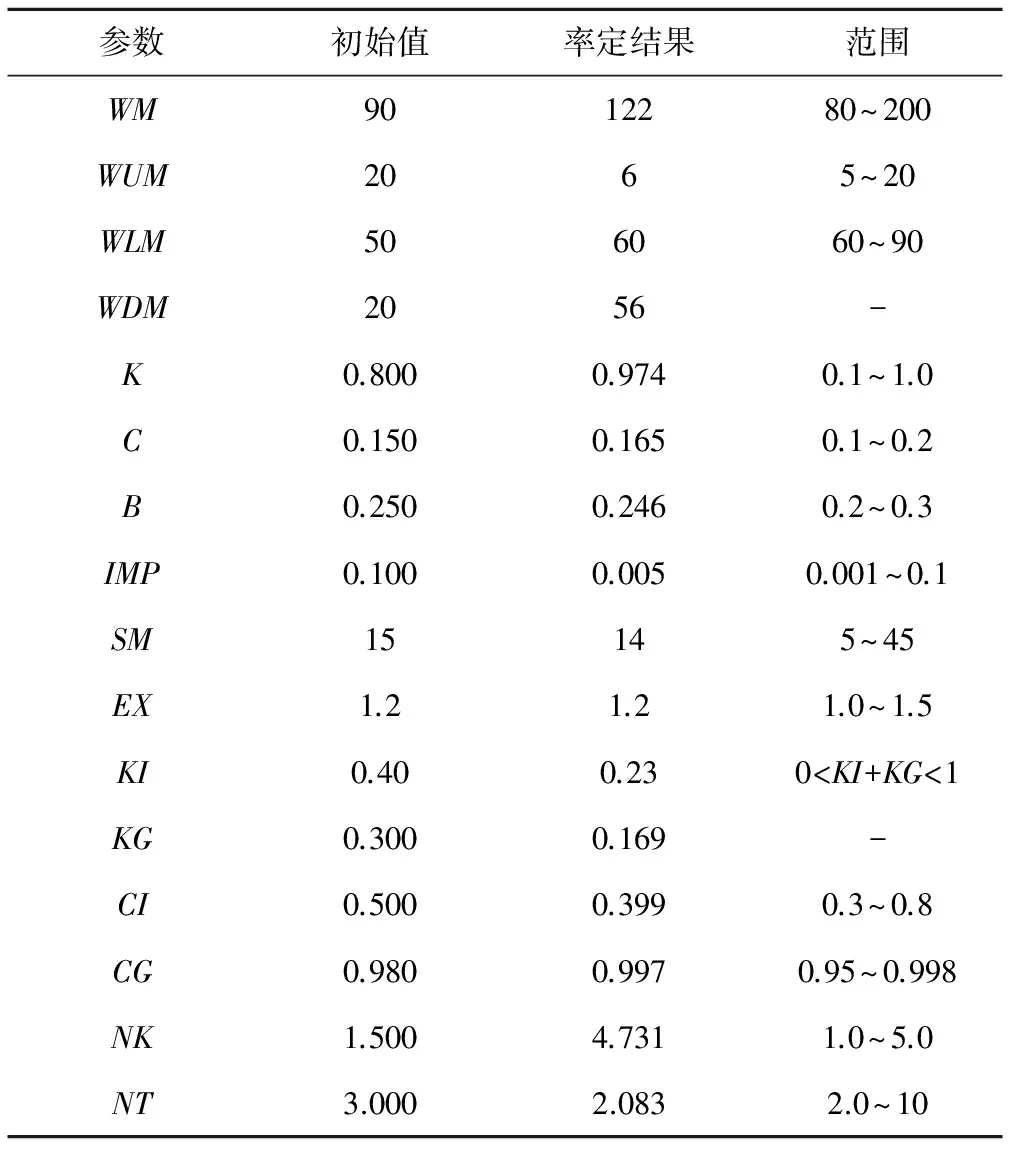
4.3 模型验证
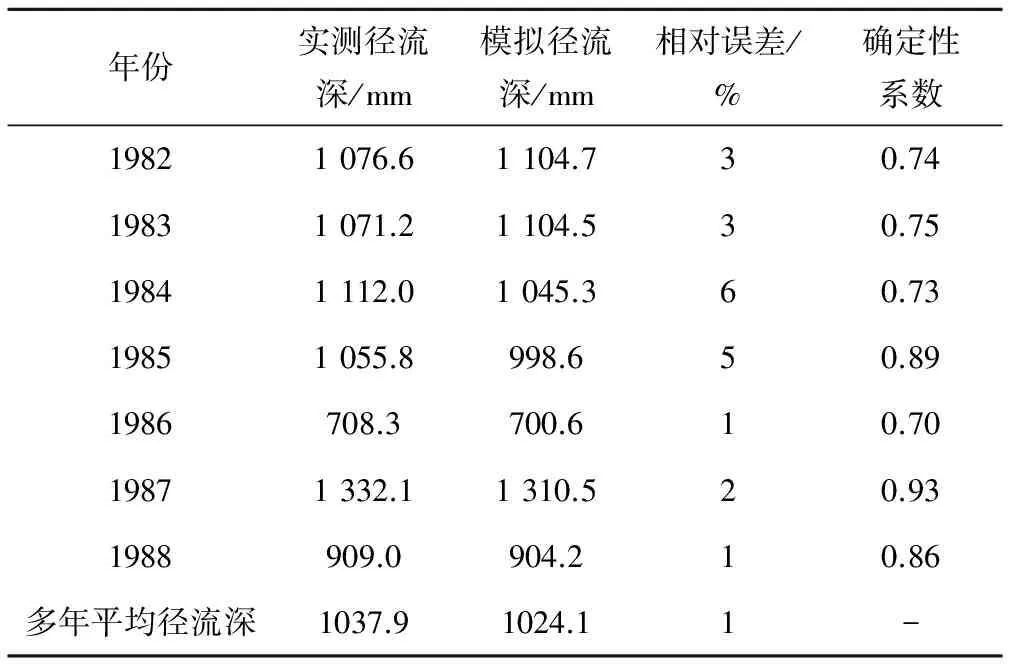
5 结 语

