基于LOFIX定位估算目标运动信息的算法研究∗

刘桂瑜 张 雷 乔 斌 凌震莹

（杭州应用声学研究所 杭州 310012）

1 引言

被动全向声纳浮标具有隐蔽性强、工作距离远、效费比高、方便携带等优点，是航空反潜最常用的一种探测器材。LOFIX利用多枚浮标收到的声源噪声强度，得出距离圆定位，是被动全向声纳浮标定位的主要方法。LOFIX的定位误差在0.5～1海里，一般用作对目标的初始定位。本文首先说明了LOFIX的定位原理，然后以连续的多次定位信息为估算样本数据，利用最小二乘法多项式拟合出目标的运动轨迹，对运动轨迹求导数可以估算出目标的速度及加速度。计算机仿真表明，在满足信噪比的情况下，对目标的速度及加速度估算的精度较高，具有一定的实际可行性，对扩大LOFIX定位的使用范围提供了一定的参考。

2 定位方法及原理分析

2.1 LOFIX定位算法流程

假设目标声源为点声源，且传输介质是各向同性的，忽略低频吸收因素，根据两个浮标接收到的同一个线谱的幅度比计算距离比，就可以确定一个目标距离圆轨迹，此圆的圆心位于两枚浮标位置的连线上并靠近接收信号大的浮标一侧。如果同时有三枚浮标收到同一跟线谱，就可以得到两个圆，得到两个可能的目标位置解［1～3］。

设浮标位置为目标实际位置为，距离圆圆心为，相应的浮标间距在直角坐标系下为d12、d13、d23，三枚浮标确定的距离圆半径为R12、R13，目标到浮标的距离为r1、r2、r3。

目标距离比：

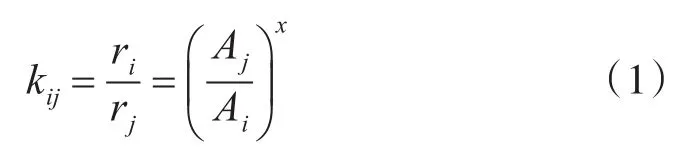
其中Aj、Ai是两枚浮标收到信号频域的幅度值，x是一个与声波传播几何衰减有关的值［4～7］（在我国海域一般使用经验值1.33）。

距离圆圆心为

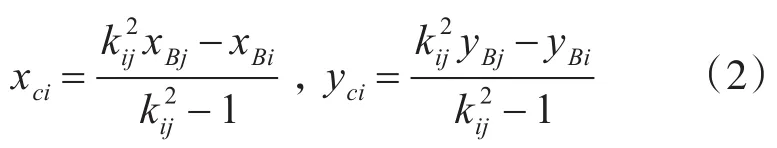
距离圆半径：

实际情况下一般同时使用至少四枚浮标进行定位，多个距离圆相交产生多个可能的目标解(xj,yj)，一般认为任一目标解与其他所有目标解的距离和最小者为真实目标解，公式如下：

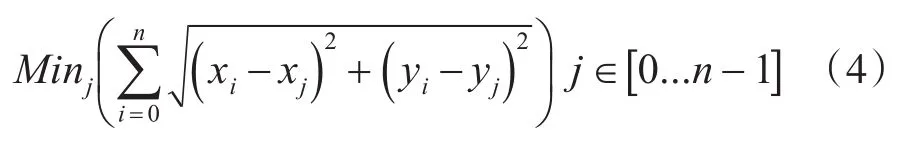
LOFIX定位的解算原理如图1所示。

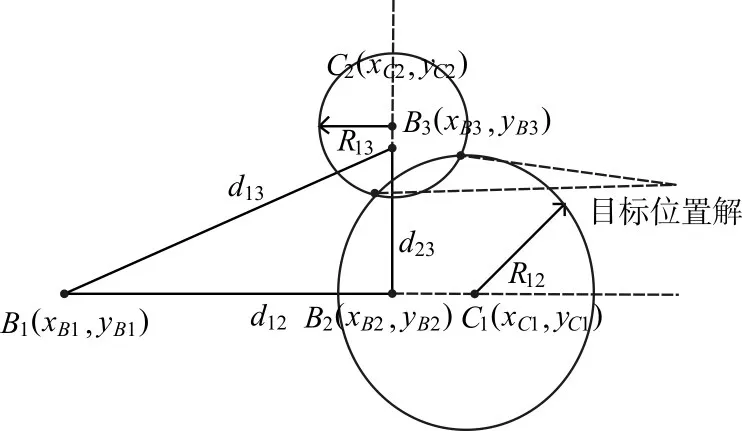
图1 LOFIX距离圆定位示意图

2.2 多项式拟合法解算目标运动信息

由LOFIX的定位原理可知，LOFIX定位只能形成目标位置信息的离散点，连续多次的定位结果可以得到观测数组，其中xi,yi为平面坐标下定位的位置信息（分别为x、y坐标），ti为定位的时间信息。假设目标的运动轨迹符合某种函数分布，浮标探测的目标速度一般较慢（相对定位时间），运动轨迹不会产生剧烈的突变，相邻的若干运动轨迹点之间有较强的相关性，则可以考虑使用基于偏差平方最小的最小二乘法多项式拟合去逼近该函数［8～10］：

设目标沿x轴运动轨迹符合多项式：

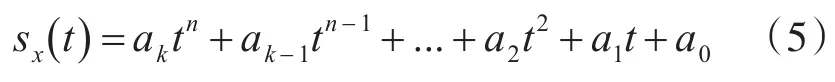
则所有观测数组的误差和：

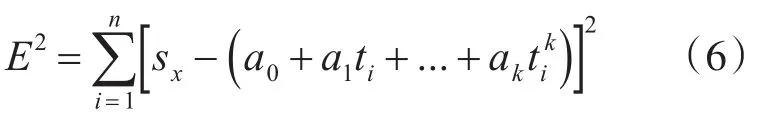
为使误差和最小，对t求偏导，并整理可得范德蒙得矩阵：

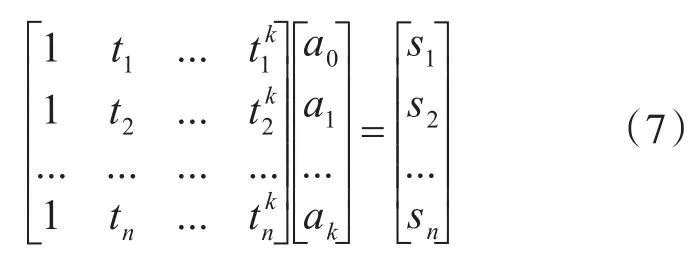
可得矩阵表达式：

由最小二乘法求解得：

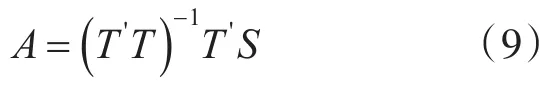
代入式（5）可以得到目标x轴运动轨迹多项式拟合表达式，对表达式求导数，分别得到目标沿x轴的速度和加速度的估算值：

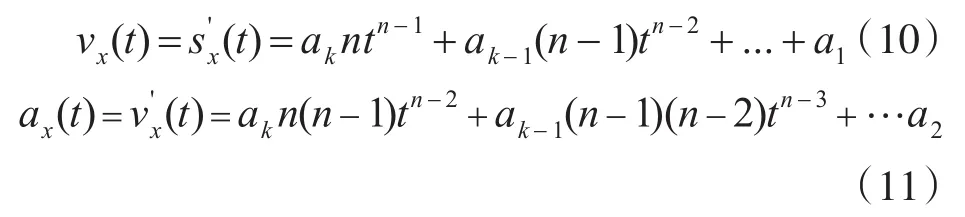
同理可以求得目标沿y轴的速度和加速度的估算值vy(t)、ay(t)，则目标的速度及加速度大小为

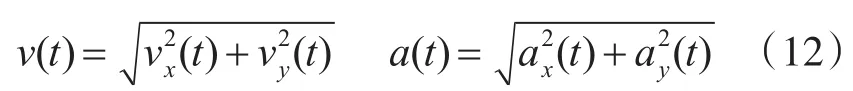
3 计算机仿真及性能分析

3.1 仿真环境条件

1）目标声源到各枚浮标的声波传播速度相同；

2）4枚浮标的坐标为，单位均为千米，目标均在各浮标的作用范围内；

3）目标产生1000Hz音频信号，声强级为190dB，由于目标距离浮标的距离较远，认为是理想的柱面衰减，即信号随距离的20*log10(r)衰减，但是实际的海洋环境是非常复杂多变的，声波传播通道很难估计，计算时使用20*log10(r1.5)衰减，浮标接收的背景噪声为均值为0、功率为1的高斯白噪声；

仿真1选择2阶多项式拟合目标运动轨迹，仿真2选择3阶多项式拟合目标运动轨迹。

3.2 仿真1

目标的运动轨迹为均速直线其中x、y轴的加速度均为0。

图2为4枚浮标时共有6个距离圆，共计12个交点，其中6个交点在目标附近，根据式（4）可以解算出单次LOFIX定位的目标位置。连续多次的目标位置解算即为图3中目标解算位置离散点，由2.2分析对这些点进行最小二乘多项式拟合，可见2阶多项式已经较好的拟合了预设目标轨迹。图4、图5为利用式（10）、（11）估算的目标的速度和加速度，可见可以较好地估算出目标的速度及加速度，加速度的估计误差比速度的估计误差稍大。

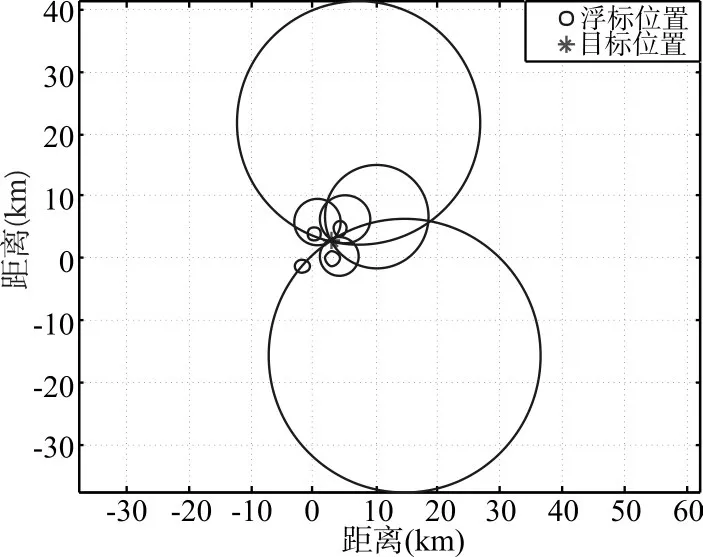
图2 单次LOFIX定位示意图

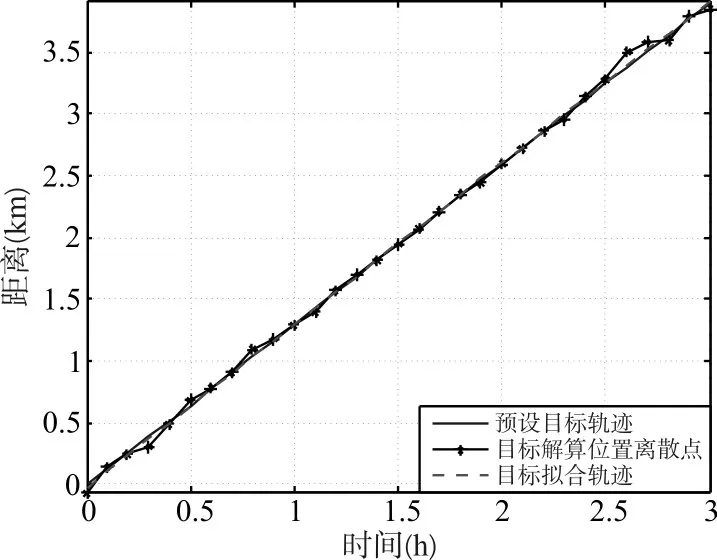
图3 目标轨迹拟合

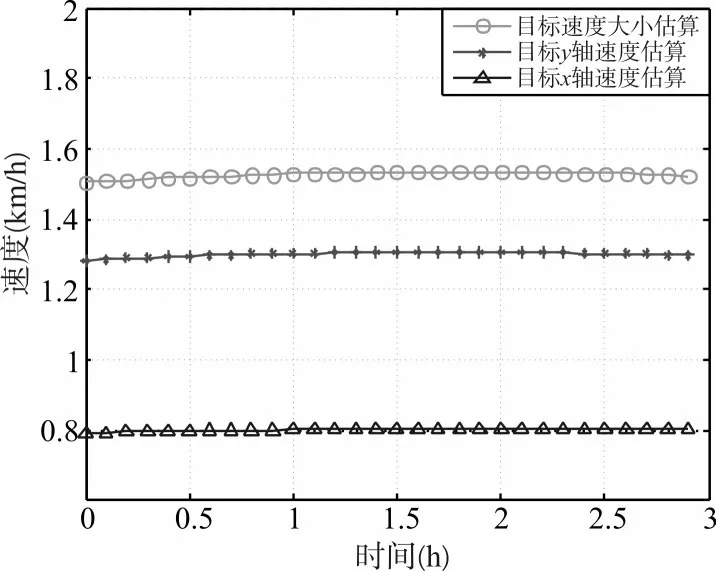
图4 x、y轴的速度估算

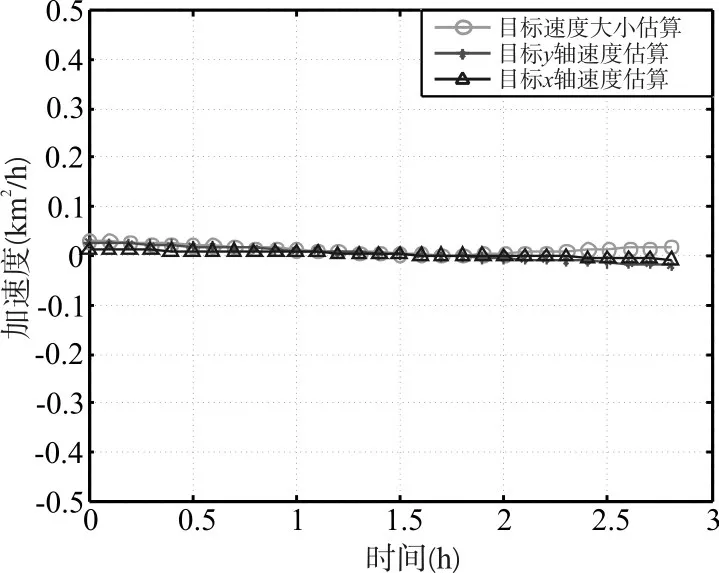
图5 x、y轴的加速度估算

3.3 仿真2

目标的运动轨迹为均加速情况：

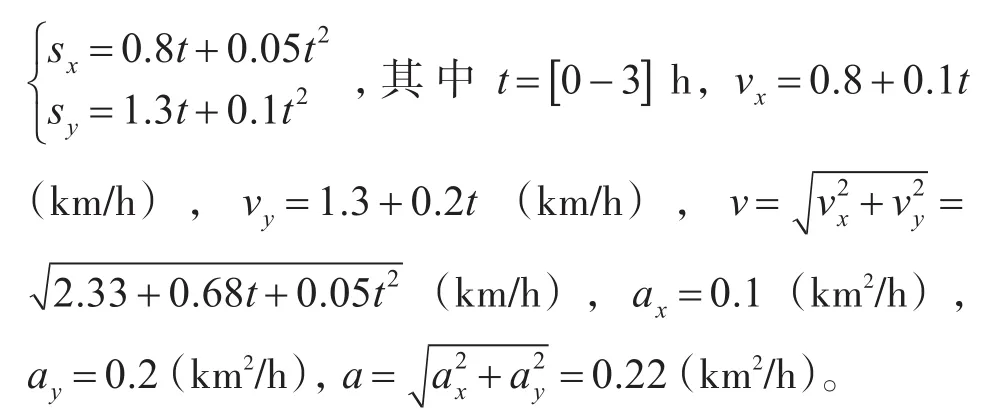
目标的单次距离圆及轨迹拟合同3.1，本仿真没有画出。图6、图7在均加速的情况下，虽然估算值与真实值之间有一定得波动误差，但是还是较好地估算了目标的速度和加速度，性能与3.1基本一致。

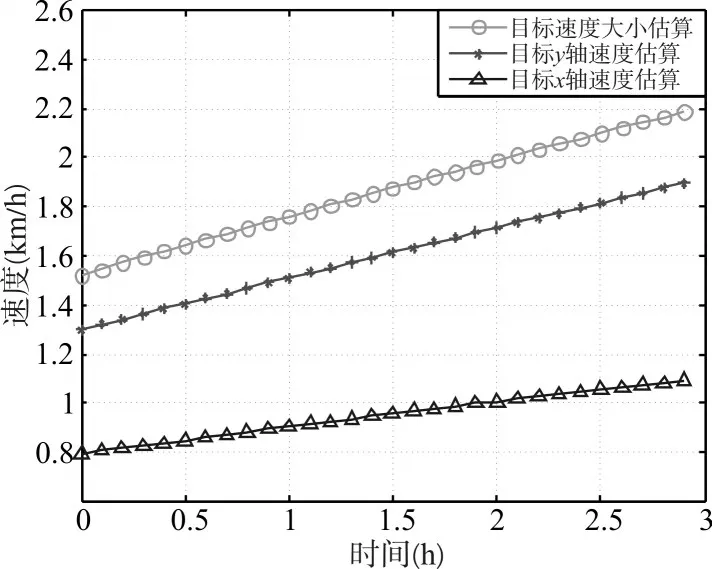
图6 x、y轴的速度估算

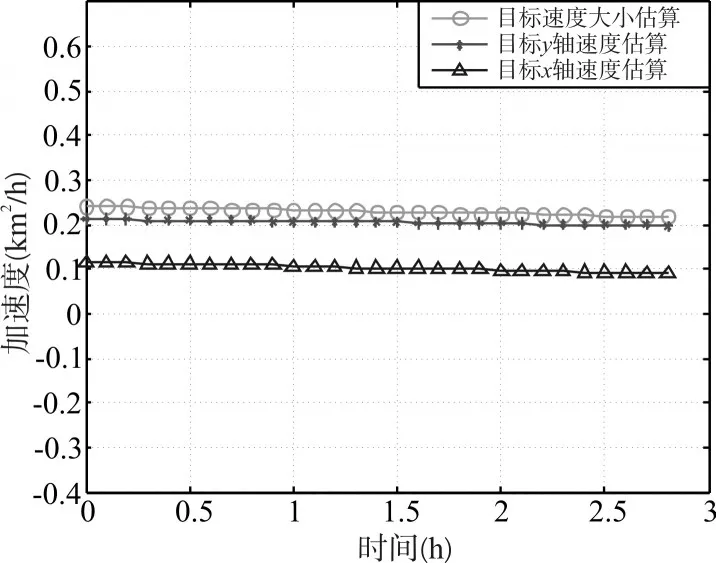
图7 x、y轴的加速度估算

3.4 仿真分析

由仿真结果可见，本文算法利用最小二乘法分别拟合目标平面坐标下x轴、y轴的运动轨迹，进而估算目标的速度及加速度的大小及方向，无论是匀速还是匀加速情况，都具有良好的性能。不仅得到了目标在两次定位信息之间的运动轨迹，而且可以得到较多的目标运动信息及态势，在一定程度上扩展了LOFIX定位算法的使用范围。然而本文在LOFIX定位时只考虑了目标信噪比的影响，实际上海洋环境具有高度的复杂性和不确定性，其中海洋声场环境对LOFIX定位的误差影响较大，并且海洋声场的模型很难建立，浮标坐标误差、浮标阵型、频域计算等因素次之。如果LOFIX定位的误差较大，那么拟合的目标运动轨迹误差也会增大，速度和加速度的估算精确会受到较大影响。另外多项式拟合试验数据时，选择合适的曲线次数是拟合效果的关键。次数过高会扩大随机误差，波定性增大，过低又不能反映数据的真实规例，次数选择不当也会对速度及加速度的估算造成影响。文献［11～13］提出了利用数据内在的规律性和观测误差来判断恰当的次数，但是都有一定的局限性。一般情况下，可以根据数据的规律，从低次到高次不断的实验，当前几项系数为0或者很小时，就可以停止了，一般不会超过8次。仿真3.1中，目标位置离散点较为平缓，3阶多项式时第一项系数已经很小，故使用2阶已经合适。仿真3.2的目标轨迹为曲线，经计算使用3阶多项式比较合适。

4 结语

LOFIX作为被动全向浮标的一种主要的定位方法，具有造价低、经济性好的优点。多在搜潜的初始阶段使用，多数情况下，还需要使用被动定向或主动全向浮标做进一步的精确定位。如果对LOFIX定位得到的连续的位置信息对进一步的处理，则可以估算出目标的更多的运动信息，提高作战效率，在一定程度上扩大了被动全向浮标的使用范围。

参考文献

［1］孙明太.航空反潜战术［M］.北京：军事科学出版社，2003：80-85.

［2］赵绪明.航空搜潜战术模型与仿真研究［D］.烟台：海军航空工程学院，2005：100-106.

［3］杨福渠.被动声纳浮标距离比定位［J］.大连：声学与电子工程，2000：78-82.

［4］凌国民，王泽民.声纳浮标技术及其发展方向［J］.声学与电子工程，2007，3：1-5.

［5］潘勤升.被动定向声纳系统［J］.声学技术，1992，11（1）：76-78.

［6］田坦，刘国枝，孙大军.声纳技术［J］.哈尔滨：哈尔滨工程大学出版社，2006：124-126.

［7］李守军，包更生，吴水根.水声定位技术的发展现状与展望［J］.海洋技术，2005，24（1）：130-135.

［8］张小凤，赵俊渭，马忠成.基于加权最小二乘的双基地声纳定位算法研究［J］.声学学报，2004，29（3）：284-286.

［9］袁文湘，孙文瑜.最优化理论方法［M］.北京：科学出版社.1997：100-102.

［10］张小凤，张光斌，赵俊渭.基于最佳线性数据融合的双基地声纳定位优化算法［J］.应用声学，2004，23（3）：40-44.

［11］谭子明.试验曲线多项式拟合时次数的统计推断［J］.工程数学学报，1987，4（2）：102-105.

［12］王连加.多项式拟合铁磁材料的磁滞回线曲线［J］.大学物理实验，2006，19（3）：58-61.

［13］吴刚.隐含多项式曲线曲面拟合次数的确定研究［J］.计算机研究与发展，2007，44（1）：148-153.