含水率与采出程度关系理论曲线建立新方法

张宏友，邓琪，王美楠，王月杰

（中海石油（中国）有限公司天津分公司渤海石油研究院，天津 300459）

0 引言

水驱油藏开发过程中，反映其开发效果的关键曲线为含水率与采出程度曲线。通过该曲线的理论对比分析，可以评价油藏不同阶段的开发效果，为油田调整挖潜提供方向，因此理论曲线的准确建立至关重要。目前，理论曲线的绘制主要有流管法和相对渗透率法［1］。流管法建立的含水率与采出程度关系曲线基于一维流动［2-3］，由于该方法过于繁琐，且公式复杂，因此在油田实际研究中应用较少。基于相渗曲线计算含水率与采出程度理论曲线，由于其公式简单，容易操作，目前是油田普遍采用的分析方法。

近年来，国内外学者针对相渗曲线表达形式开展了大量研究［4-13］，尽可能使理论曲线更加接近实际曲线。但相渗曲线法计算含水率与采出程度关系理论曲线仍然存在2个问题：一是缺少无水采油期开发阶段；二是采出程度计算过程中的平均含水饱和度直接采用出口端含水饱和度来代替，或利用基于一维流动Weldge方程建立的平均含水饱和度与出口端含水饱和度关系，或利用1958年艾富罗斯基于一维流动、油水黏度比在1～10的平均含水饱和度与出口端含水饱和度实验结果，存在一定的局限性［14-17］。

实际上，对于水驱油藏来说，水驱过程可以分为见水前的无水采油期和见水后的含水上升期2个阶段。本文利用流管模型，以反九点注采井网为基础，分别建立无水采油期采出程度、含水上升期含水上升率的理论变化关系式。在此基础上，建立了一种含水率与采出程度关系理论曲线研究新方法。

1 方法的建立

1.1 流管模型建立与求解

油藏从注水井到生产井的渗流场，可视为一系列的曲线流管。对于均质油藏反九点注采井网，其渗流场可分为边井和角井 2个单元（见图 1、图 2）［18-19］。由渗流力学可知，流管中的油水两相渗流可表示为［19］

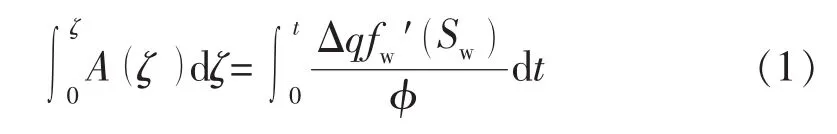
式（1）即为曲线流管下的等饱和度平面移动公式。

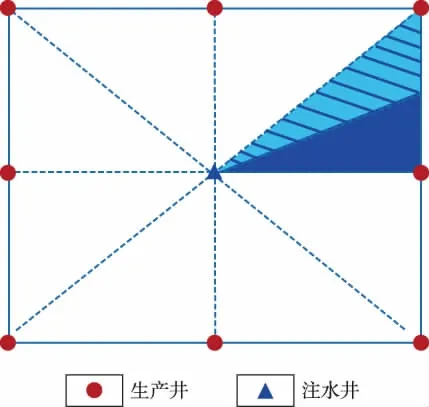
图1 反九点注采井网单元示意

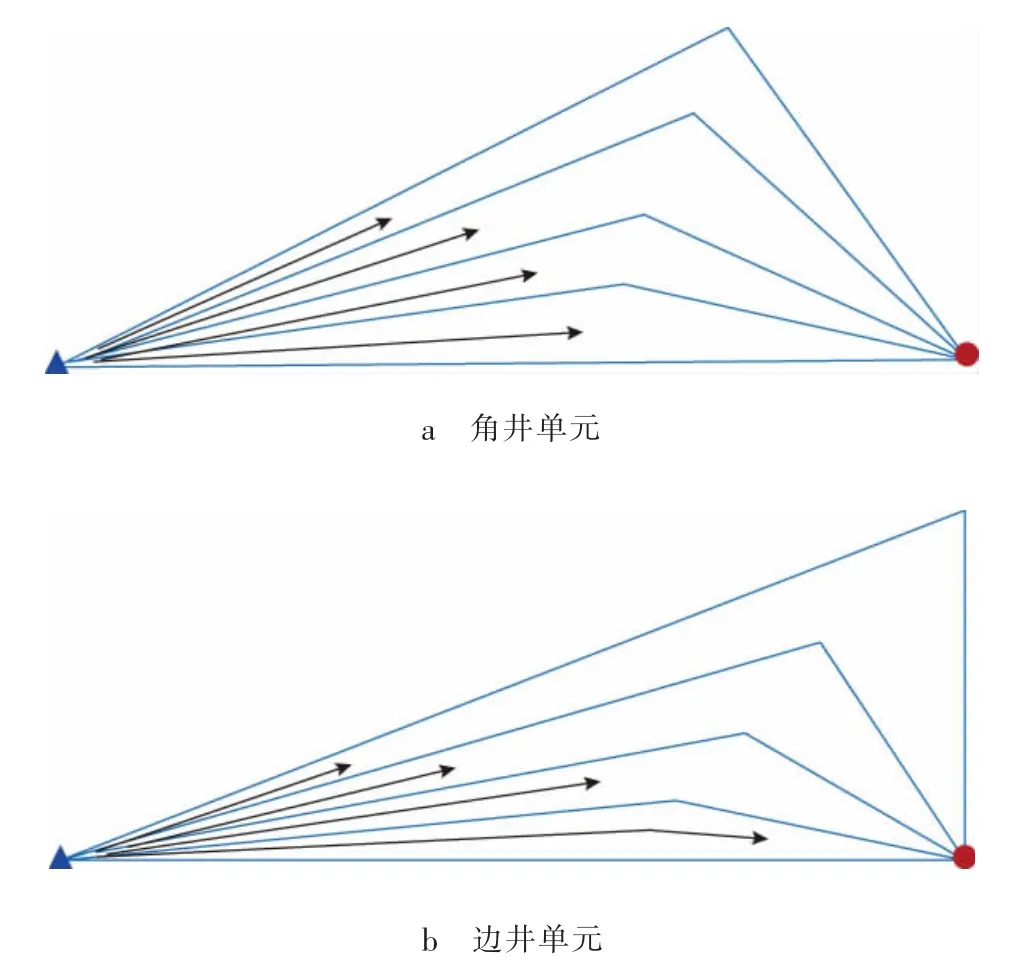
图2 反九点注采井网基本单元流管形态示意

每根流管中，水驱油渗流阻力为

t时刻每根流管中的流量为

联合式（1）—（3），即可求解图2所示基本注采单元中含水饱和度在每一根流管中不同时刻的分布。

对于水驱油藏来说，水驱规律主要受水油流度比和油水相渗曲线的影响。对于图1所示注采井网中油水两相渗流流管模型，采用MATLAB编制相应求解程序，开展无水采油期采出程度、含水上升期含水上升率与水油流度比、油相指数、水相指数、残余油饱和度、束缚水饱和度的理论变化规律研究，设计5个影响因素共计648组方案开展研究（见表1）。

表1 油藏模型方案设计参数

1.2 无水采油期采出程度

1.2.1 影响因素

数值模拟结果表明，在其他4项影响因素保持不变条件下，无水采油期采出程度与水油流度比呈幂函数关系（见图3），相关系数接近1.0。由图3可以看出，随着水油流度比增加，水相相对于油相的渗流能力增加，水驱前缘突破速度加快，无水采油期采出程度逐渐降低，尤其是当水油流度比小于50时，无水采油期采出程度急剧下降。

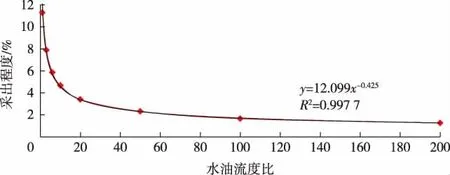
图3 理论无水采油期采出程度与水油流度比关系

数值模拟结果表明，在其他4项影响因素保持不变条件下，无水采油期采出程度与水相指数（见图4）、油相指数、束缚水饱和度、残余油饱和度均呈线性关系。

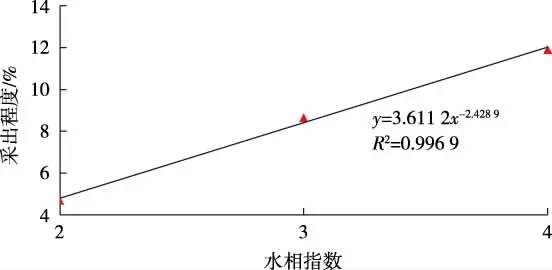
图4 理论无水采油期采出程度与水相指数关系

1.2.2 变化关系式的建立

首先假定水油流度比不变，构建无水采油期采出程度与其他4个影响因素之间的多元线性关系式：

利用SPSS多元线性回归法，得到不同水油流度比条件下系数 b0—b4（见表 2）。

表2 不同水油流度比条件下系数b0—b4结果统计

在此基础上，进一步开展系数b0—b4与水油流度比变化规律研究。结果表明，系数b0—b4均与水油流度比呈幂函数关系。图5为b2与水油流度比的关系。

图5 回归系数b2与水油流度比关系

将系数b0—b4拟合回归得到的幂函数关系式代入式（4），最终得到无水采油期采出程度与5个影响因素之间的理论变化关系式：

1.3 含水上升期含水上升率

1.3.1 和 Sw 关系式的建立

利用数值模型得到的含水饱和度场，对见水后的出口端含水饱和度与平均含水饱和度进行分析，发现两者在不同水油流度比条件下均类似线性关系。特别是在低水油流度比条件下，由于活塞式驱替较强，且角井、边井见水时间不同，导致2个含水饱和度的线性关系稍差；当水油流度比较大时，由于非活塞式驱替较强，使得2个含水饱和度呈现出相关系数近似1.0的线性关系。两者线性关系可表示为

在此基础上，对于式（6）中系数a的变化规律，开展相应的研究。结果表明，a在不同条件下与水油流度比均呈对数关系。通过回归分析486个方案的计算结果，得到a与不同因素之间的关系式：

其中：

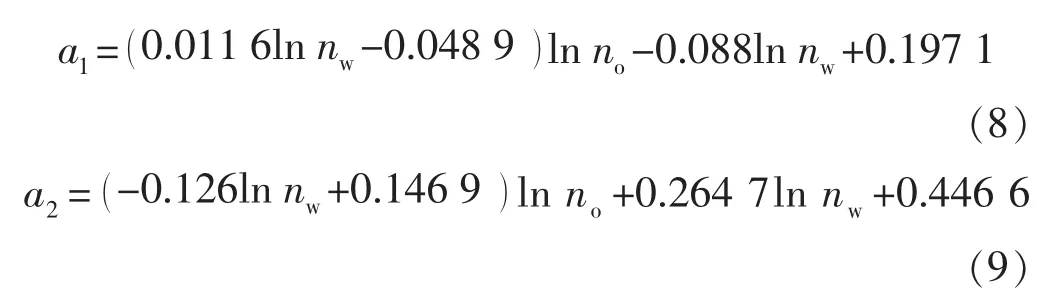
1.3.2 含水上升率计算公式的建立

含水上升率定义为每采出1%地质储量含水率的变化量，公式为

采出程度与油藏平均含水饱和度的关系式为

传统分流量方程法计算含水上升率公式为

将式（7），（11），（12）代入式（10）得到：

式（13）为新的水驱油藏理论含水上升率计算公式。该方法利用a对传统计算方法进行校正，且由式（7）—（9）可知，a的主要影响因素为水油流度比、水相指数和油相指数。

1.4 含水率与采出程度关系理论曲线建立

以无水采油期采出程度理论公式、含水上升期含水上升率公式为基础，建立水驱油藏含水率与采出程度关系理论曲线。

无水采油期：利用式（5）计算无水采油期采出程度R0。 显然，当 R≤R0时，fw=0。

含水上升期（R＞R0）：

1）划分含水率变化步 Δfw（Δfw=0.1%）。

2）计算第1步末含水率。

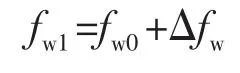
3）计算第1步平均含水率。

4）根据含水率与含水上升率关系理论曲线，得到第1步含水上升率fw1′。

5）计算第1步末采出程度。

6）重复步骤2）—5），最终得到水驱油藏含水率与采出程度关系理论曲线（见图6）。

图6 含水率与采出程度关系

从图6可以看出，随着地层原油黏度的增加，无水采油期采出程度越来越小，含水上升期含水上升规律由凹型逐渐变化到S型、凸型，表明新方法建立的含水率与采出程度关系理论曲线能够客观反映不同流体性质、不同相渗曲线的水驱油藏开发规律。新方法建立的含水率与采出程度关系理论曲线，主要适用于采用反九点注采井网开发的油藏，且水油流度比在1～200。

2 实例应用

将油田含水率与采出程度关系实际曲线与理论曲线绘制在同一坐标系中，并引入评价系数，对比同一含水条件下实际曲线与理论曲线的偏离程度，评价水驱开发效果的好坏。评价系数越大，水驱开发效果越好。该方法已成功应用于渤海油田多个中高含水期、高含水期的水驱油藏开发效果评价，评价结果客观合理，与油田开发认识一致。

渤中28-2S油田1167砂体含油层系位于明下段，属于浅水三角洲相沉积，为典型的高孔、高渗轻质油藏。地层孔隙度为29.6%，渗透率1 682×10-3μm2，地层原油黏度 11.74 mPa·s，地层水黏度 0.50 mPa·s，束缚水、残余油饱和度分别为0.289和0.215，水、油相指数分别为1.67和1.95，束缚水饱和度下油相相对渗透率1.00，残余油饱和度下水相相对渗透率0.31。应用本文新方法建立含水率与采出程度关系理论曲线，并将其与实际曲线绘制在同一坐标系中（见图7）。从图7可以看出，实际曲线与理论曲线变化趋势基本一致，且两者比较接近，计算评价系数为0.92，说明1167砂体开发效果较好。另外，在产能建设期，由于1167砂体采取开发井分批次投产的策略，实际无水采油期采出程度与理论值差异较大。对不同批次开发井投产时间进行归一化处理后，发现实际无水采油期采出程度与理论值基本一致，也证明了新方法的正确性。

图7 渤中28-2S油田1167砂体含水率与采出程度评价

3 结论

1）开展无水采油期采出程度与5项影响因素之间的理论变化规律研究，并拟合回归得到其理论变化关系式。

2）统计发现，含水上升期油藏出口端含水饱和度与平均含水饱和度呈近似线性变化，并以此为基础提出了计算水驱油藏理论含水上升率的新方法。

3）基于无水采油期采出程度、含水上升期含水上升率的理论变化关系式，建立了一种新的含水率与采出程度关系理论曲线研究方法，解决了传统相渗曲线法的不足。

4）实例应用表明，利用本文新方法建立的含水率与采出程度关系理论曲线能够评价水驱油藏的开发效果，评价结果客观合理，值得推广应用。

4 符号注释

Δq为单根流管流量为流线长度ζ处的流管截面积，m2；ζ为以注水井为起点的流线长度，为含水率随含水饱和度的变化率；ri为单根流管渗流阻力，MPa·（m3/s）-1；φ 为孔隙度；t为时间，s；rw为井半径，m；ζ2为以注水井为起点的水驱前缘处流线长度，m；ζ1为以注水井为起点的纯水区流线长度，m；Kro为油相相对渗透率；Krw为水相相对渗透率；μo为地层油黏度，mPa·s；μw为地层水黏度，mPa·s；li为单流管流线总长度，m；K 为储层渗透率，10-3μm2；Q 为基本渗流单元流量，m3/s；nw为水相指数；no为油相指数；λ为水油流度比；Swi为束缚水饱和度；Sor为残余油饱和度；R为采出程度；R0为无水采油期采出程度；为平均含水饱和度；fw为含水率；fw′为含水上升率；Swi，分别为2个相邻阶段对应出口端含水饱和度；fw0′为传统方法所计算含水上升率；Sw为出口端含水饱和度；a，b为油藏平均含水饱和度与出口端含水饱和度变化关系系数分别为2个相邻阶段对应含水率分别为2个相邻阶段对应采出程度；R1为第1步末对应采出程度；Δfw为含水率变化率；fw1，fw0分别为第1步末、第1步初对应含水率；为第1步平均含水率；fw1′为第1步含水上升率。

［1］凡哲元，袁向春，廖荣凤，等.制作含水率与采出程度关系理论曲线常犯错误及解决办法［J］.石油与天然气地质，2005，26（3）：384-387.

［2］冯其红，吕爱民，于红军，等.一种用于水驱开发效果评价的新方法［J］.石油大学学报（自然科学版），2004，28（2）：58-60.

［3］张宏友，邓琪，牟春荣，等.水驱砂岩油藏理论含水上升率计算新方法：对分流量方程法的校正［J］.中国海上油气，2015，27（3）：79-83.

［4］金蓉蓉.新型含水率与采出程度关系曲线的推导［J］.大庆石油地质与开发，2015，34（3）：72-75.

［5］陈元千，陶自强.高含水期水驱特征曲线的推导及上翘问题的分析［J］.断块油气田，1997，4（3）：19-24.

［6］李丽丽，宋考平，高丽，等.特高含水期油田水驱规律特征研究［J］.石油钻探技术，2009，37（3）：91-94.

［7］刘世华，古建伟，杨仁峰.高含水期油藏特有水驱渗流规律研究［J］.水动力学研究与进展：A 辑，2011，26（6）：6-9.

［8］宋兆杰，李冶平，赖枫鹏，等.高含水期油田水驱特征曲线关系式的理论推导［J］.石油勘探与开发，2013，40（2）：201-208.

［9］张金庆，孙福街，安桂荣.水驱油田含水上升规律和递减规律研究［J］.油气地质与采收率，2011，18（6）：82-85.

［10］陈明仁，蒋林，李成刚，等.能量指示曲线叠合图版提高碳酸盐岩油藏采收率应用研究［J］.石油实验地质，2016，38（S1）：39-43.

［11］周鹏，王庆勇，张凤喜，等.预测水驱油田含水率的新模型及应用［J］.断块油气田，1995，2（2）：522-524，535.

［12］陈元千，陶自强.高含水期水驱曲线的推导及上翘问题的分析［J］.断块油气田，1997， 4（3）：19.

［13］田鸿照，彭彩珍，于雪琳，等.水驱油田开发指标的综合预测法［J］.断块油气田，2011，18（2）：238.

［14］郭印龙，郭恩常，杨永利，等.一种新的水驱开发效果评价体系［J］.石油地质与工程，2008，22（5）：67-68.

［15］高文君，徐君.常用水驱特征曲线理论研究［J］.石油学报，2007，28（3）：89-92.

［16］高文君，宋成元，付春苗，等.经典水驱油理论对应水驱特征曲线研究［J］.新疆石油地质，2014，35（3）：307-310.

［17］陈元千.水驱曲线关系式的推导［J］.石油学报，1985，6（2）：69-78.

［18］计秉玉，李莉，王春艳.低渗透油藏非达西渗流面积井网产油量计算方法［J］.石油学报，2008，29（2）：256-261.

［19］吕栋梁，唐海，郭粉转，等.低渗透油田反九点井网面积波及效率影响研究［J］.西南石油大学学报（自然科学版），2012，34（1）：147-152.