一种联合式射频窄带信号时差估计方法

葛云露，吴 梦，姬生云

(1. 中国电子科技集团公司第二十二研究所，山东青岛 266107; 2.北京新能源汽车股份有限公司青岛分公司，山东青岛 266600)

0 引 言

辐射源无源定位由于其作用距离远、隐蔽性强，在电磁频谱监测、检测、感知组网等领域具有十分重要的地位和作用[1-2]。相较于测向定位技术，基于时差估计的无源定位技术，系统实现简单，不需要架设复杂的测向站, 利用已有的监测站就可实现干扰源的定位，易于组网，升级改造方便，定位精度高等优势。

目前，基于时差估计的射频宽带信号无源定位技术已得到推广及应用[3-5]，依据时差估计的克拉美罗界定义可知[6-7]，信号的带宽越窄，时差估计算法的精度越低，射频窄带信号由于其信号带宽窄，易受噪声干扰，射频窄带信号的时差估计精度低，无法电磁频谱感知对窄带无源信号定位的要求。因此，开展射频窄带信号的时差估计方法研究，对于提升电磁频谱感知的监测、检测、组网能力，具有十分重要的现实意义。

针对射频窄带信号的时差估计，本文提出了一种联合式射频窄带信号时差估计方法，本方法在离散小波变换与广义互相关时差估计方法结合的基础上，通过对时差估计结果的进一步聚类分析，有效的降低时差估计孤立值、错误值的影响，得到了高精度的射频窄带信号的时差值。仿真结果表明，本方法具有良好的估计性能，射频窄带信号时差提取精度显著提高。

1 联合式射频窄带信号时差估计方法原理

1.1 时差估计信号模型

射频窄带信号时差估计数学模型如下式所示[8]。

其中，s(t)为射频窄带信号，n1(t)和n2(t)为加性噪声，D为同一信号到达两个接收机的相对时差，α表示幅度衰减系数。信源s(t)、噪声n1(t)和n2(t)均为互不相关的高斯白噪声，频率范围为(-fc，fc)kHz，三者都是平稳的且互不相关。

1.2 基于离散小波变换低频分量提取

小波变换是傅立叶分析思想方法的发展与延拓。它既继承和发展了短时傅立叶变换的局部化思想，同时又克服了窗口大小不随频率变化的其缺点，是信号时频分析、处理时变非稳态信号的理想工具。通过进行多分辨率分析(Multi resolution Analysis)分析，提取时差信号的低频分量，作为时差提取数据源[9-11]。

离散小波函数Ψj,k(t)：

其中，a0∈R+,且a0≠0，b0∈R，j,k∈Z。

离散小波变换系数为：

重构公式为：

双尺度函数的双尺度方程：

小波函数的双尺度方程

设f(x)在子空间Vj和Wj的投影系数分别为cj,k和dj,k，即：

(f(x),φj,k(x))=cj,k；j,k∈Z

(f(x),Ψj,k(x))=dj,k；j,k∈Z

则各层之间有分解关系式为：

相应的重构关系式为：

j,k∈Z

图2为一维信号的三层多分辨分析树结构，C表示低频，D表示高频，末尾序号表示分解层数。

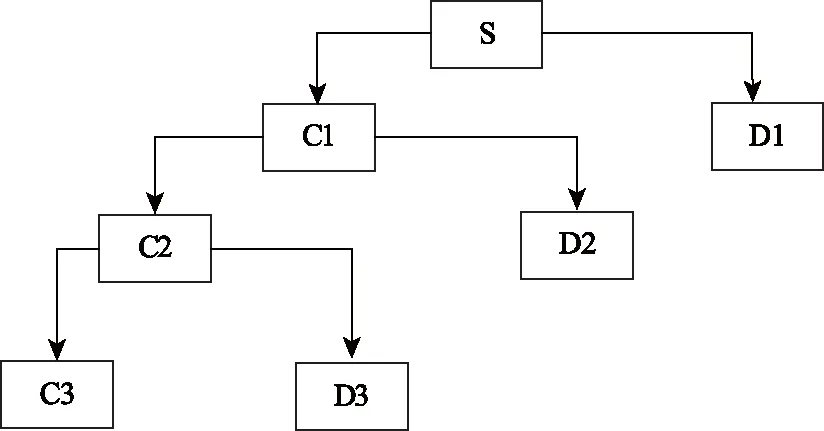
图1 三层多分辨分析分解树示意图

1.3 基于广义互相关法时差估值提取

广义相关法时差估计[8]实现简单，复杂度较低。通过对相关函数做峰值检测即可得到估计的时差值。广义相关法时差估计原理图如图2所示。

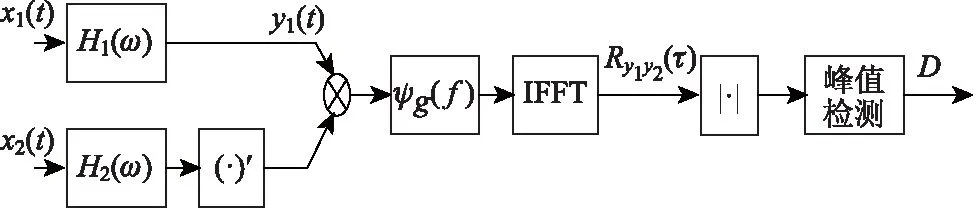
图2 广义相关法时差估计原理图

其中：ψg(f)为广义相关法的加权函数，(·)′为共轭运算，|·|表示取模值，D为估计的时差值。

根据维纳- 辛钦定理，相关函数Rx1x2(τ)与其互功率谱Gx1x2(ω)有傅里叶变换对关系：

由图1的广义相关法原理图可得y1(t)和y2(t)相关函数为Ry1y2(τ)，再根据相关检测原理进行峰值检测，得到的时差估计值D为：

D=Argmax{|Ry1y2(τ)|}

1.4 基于聚类分析方法时差估值提取

通过广义相关法时差估计可快速估计出各个时段的时差估计值，但由于信号传播的环境复杂，时差估计值往往分布零散，估计偏差较大，以广义互相关时差估计值为输入，通过聚类分析算法可深度挖掘各时差估值的内在联系值的统计特性和相关性，进一步提高时差估计的精准度。

采用聚类算法是K-means算法[12-13]，也被称为k-平均或k-均值，是一种迭代的聚类算法，迭代的过程中不断地移动簇集中成员，直至得到理想的簇集为止。利用K-means算法聚类算法得到的簇，簇中成员间的相似度很高，同时不同簇中成员之间的相异度也很高。通过K-means聚类算法可有效地降低异常值对时差估计精度带来影响，从而将一步提高时差定位的精度。详细流程如下：

(1)将所有得到的时差初值随机分配到k个非空的簇中。

(2)计算每个簇的平均值，并用该平均值代表相应的簇。

(3)根据每个对象与各个簇中心的距离，分配给最近的簇。

(4)然后转(2)，重新计算每个簇的平均值。

(5)达到最大迭代次数，迭代停止，最大迭代次数为时差初值的个数。

(6)当两个簇中心的距离小于时差估计误差范围时，将两个簇合并。

(7)最大的簇的中心值即为时差估计值终值。

2 联合式射频窄带信号时差估计方法流程

本文提出的联合式射频窄带信号时差估计方法是以各监测站的I/Q数据为数据源。根据监测设备的采集周期，对周期内的监测数据进行DWT变换，提取其低频小波系数。并基于广义互相关时差提取方法，以低频小波系数为数据源，完成时差初值的估计。最终通过对大数据量的时差初值进行聚类分析，得到射频窄带信号的时差估计值。

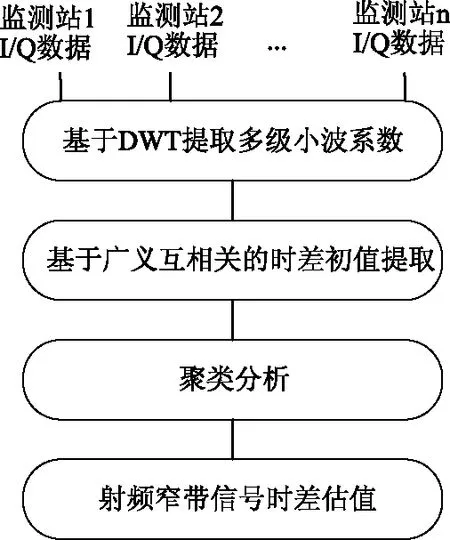
图3 联合式射频窄带信号时差估计方法流程

3 仿真与分析

为了分析基于GCC-DWT与K-means聚类的联合式窄带信号时差估计方法的性能，以对讲机为信号源，发射FM窄带信号，使用EB信道模拟器设置时延为-100 ns，2台信号监测接收机，采集100组信号，进行GCC与GCC-DWT时差估计法，与GCC-DWT联合K-means聚类法的时差估计方法进行仿真分析和比较。

首先，分别进行高信噪比(30 dB)和低信噪比(10 dB)环境进行GCC法与GCC-DWT法仿真分析。

(1) 接收信噪比为30 dB，分别采用GCC法与GCC-DWT法提取100组时差估计值，如图4所示。

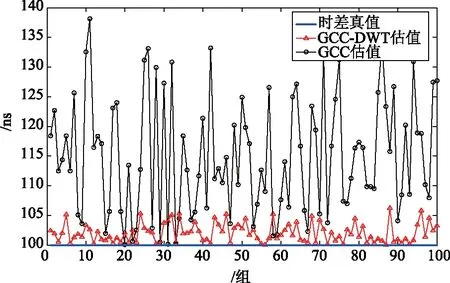
图4 接收信噪比为30 dB时，GCC法与GCC-DWT法仿真结果对比

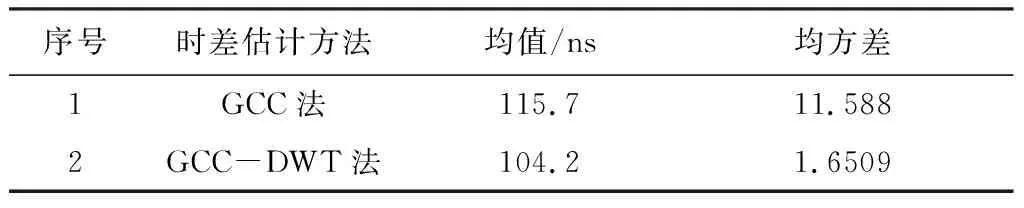
序号时差估计方法均值/ns均方差1GCC法115.711.5882GCC-DWT法104.21.6509

(2)收机信噪比为10 dB，分别采用GCC法与GCC-DWT法提取100组时差估计值，如图5所示。

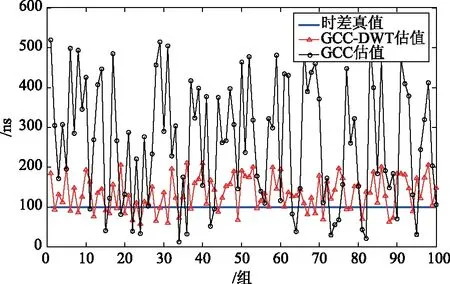
图5 接收信噪比为10 dB时，GCC法与GCC-DWT法仿真结果对比

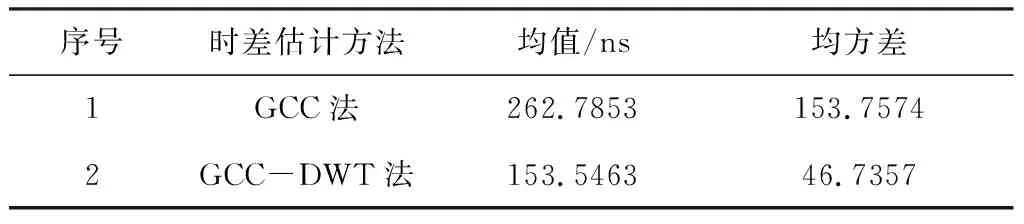
序号时差估计方法均值/ns均方差1GCC法262.7853153.75742GCC-DWT法153.546346.7357

通过以上实验结果可以看出： GCC-DWT法的时差估计精度整体上要优于GCC算法的精度; 接收机信噪比为30 dB的环境下，GCC-DWT法的时差估计均值为104.2/ns，GCC法的时差估计均值为115.7/ns，精度提高了9.93%；接收机信噪比为10 dB 的环境下，GCC-DWT法的时差估计均值为153.5463/ns，GCC法的时差估计均值为262.7853/ns，精度提高了41.57%，将DWT与GCC算法结合可以有效地提高时差估计进度精度。通过两种环境下两种算法的均方误差可以看出，GCC-DWT法的稳定性更高，优于GCC法。

下面进行 GCC-DWT联合K-means聚类法的时差估计法仿真分析。

基于GCC-DWT联合K-means聚类的窄带信号时差估计方法时差估计结果如表3、表4所示。

表3 接收机信噪比为30 dB时，GCC-DWT联合K-means聚类法时差估计结果

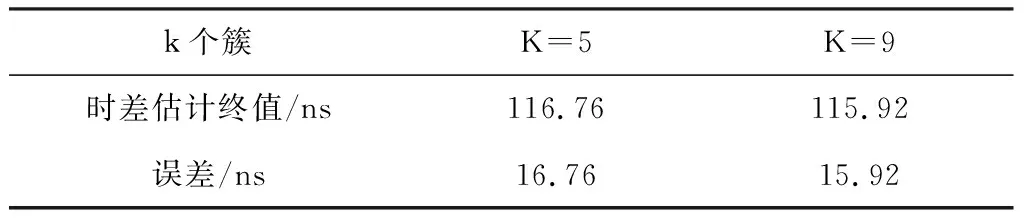
表4 接收机信噪比为10 dB时，GCC-DWT联合K-means聚类法时差估计结果

通过以上实验可以看出，本文提出的基于GCC-DWT联合K-means聚类的时差估计方法具有良好的窄带信号的时差估计能力。接收机信噪比为30 dB时，GCC法的时差估计均值为115.7/ns，基于GCC-DWT联合K-means聚类的时差估计方法的时差终值为101.92/ns，精度提高了11.9%；接收机信噪比分别为10dB时，GCC法的时差估计均值262.785 3/ns，基于GCC-DWT联合K-means聚类的时差估计方法的时差终值为116.76ns，精度提高了55.71%，本文提出的联合式窄带信号时差估计方法的时差估计精度显著提高。

4 结 语

本文针对射频窄带信号的时差估计问题开展了研究，提出了基于GCC-DWT联合K-means聚类的时差估计方法，并与经典的广义互相关算法与传统的相关法进行了实验对比。从实验结果可以看出，本算法优于经典的广义互相关算法，更适合于窄带信号的时差估计。目前，本算法进行了实验室仿真，尚未验证算法对散射、绕射、多径等共存的传播环境下的鲁棒性，将在后续研究中进一步实验，对算法进行改进和完善。

：

[1] 王先义，陈丹俊，刘斌等.复杂电磁环境战场频谱管理[J]．中国电子科学研究院学报，2008，3(4)：338-344.

[2] 胡来招． 无源定位[M]． 北京: 国防工业出版社，2004.

[3] 陈明福，戴琳琳. 无源定位系统在航管中的应用[J]. 现代雷达，2011(07)：32-36

[4] 郑志娟，刘建.多站时差定位技术提升野战机场航管与空情监视能力[J].舰船电子对抗，2011(04)：9-13

[5] Glenn Goodman, Lethal SEAD. US navy and US air force pursue different paths to counter SAW threats [ J] . The Journal o f Electronic Defense, 2009, 32(4):26-34.

[6] Friedlander B．On the Cramer-Rao bound for time delay and Doppler estimation[J]．IEEE Transactions On Information Theory， 1984，30(3): 575-580．

[7] Zeira A，Schultheiss P M. Realizable lower bounds for time delay estimation[J]．IEEE Transactions On Signal Processing，1993，41(11): 3102-3113．

[8] Kapp C H, Cater G C. The generalized correlation method for estimation of time delay [ J ]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1976,24(4): 320- 327.

[9] 杨福生.小波变换的工程分析与应用[M].北京科学出版社,1999.

[10] 胡昌华，张军波，夏军等.基于MATLAB的系统分析与设计-小波分析[M].西安电子科技大学出版社，2000.

[11] Castleman K G 著，朱志刚等译.数字图像处理[M].电子工业出版社，1998(第一版)：261-304.

[12] Dunhm M H 著，郭崇慧等译. 数据挖掘教程[ M] .清华大学出版社, 2005.

[13] Mitchell T M 著，曾华军等译. 机器学习[M]. 机械工业出版社，2015.