An improved theoretical procedure for the pore-size analysis of activated carbon by gas adsorption☆

Guodong Wang ,Jianchun Jiang *,Kang Sun ,Jianzhong Wu **

1 College of Chemical Engineering,Nanjing Forestry University,Nanjing 210037,China

2 Department of Chemical and Environmental Engineering,University of California,Riverside,CA 92521,USA

3 Institute of Chemical Industry of Forest Products,Chinese Academy of Forestry,Nanjing 210042,China

1.Introduction

Amorphous porous carbon,also known as activated carbon,plays an important role in diverse applications in chemical engineering.Thanks to its large specific surface area and low production cost,activated carbon is promising as a viable high-capacity adsorbent for natural gas storage.Industrial applications of adsorbed natural gas(ANG)are critically dependent on the storage capacity of the adsorbent at ambient temperature and moderate pressure[1,2].The adsorption capacity of activated carbon varies significantly due to the variety ofcarbon sources and porous structures.Pore-size analysis is useful for the rational selection of different kinds of activated carbon and other amorphous materials with good performance[3,4].

The adsorption capacity of activated carbons varies widely depending on the activation process.Gas adsorption has been considered as the primary method for the characterization of the pore-size distribution.Conventional methods are often concerned with materials surface area based on the Brunauer–Emmett–Teller(BET)adsorption model or,more recently,the classical density functional theory(CDFT).While much attention has been given to the reliability of the BET or CDFT predictions of specific surface area,much less is known on the usefulness of these methods for predicting the pore-size distribution and adsorption capacity at conditions different from materials characterization.While both BET and DFT method shave been routinely used forcharacterization of porous materials,rarely questioned are the accuracy of the theoretical models,as wellas the related numerical procedures,fordetermining the pore-size distributions.Furthermore,little is known on the reliability of traditional theoretical methodology,the mean- field approximation in particular,to describe gas-adsorption isotherms[5].

Previous efforts to improve the theoretical procedure for materials characterization can be classified into two categories.On the one hand,one may improve the thermodynamic model to describe adsorption isotherms by using novel DFT functionals[6–9],a better equation of state for bulk systems[10–12],or a more accurate potential to represent gas–gas and gas–substrate interactions[13].On the other hand,one may take into consideration multi-aspects of porous materials including the surface defects[14,15],various kinds of pore geometries[16,17],and properties related to the intrinsic amorphous nature of porous materials[18,19].

In this paper,we calibrate four different versions of free-energy density functionals that are potentially useful for the pore-size analysis of amorphous porous materials.Using molecular simulation and experimental data as a benchmark,our objective is to identify a reliable computation procedure to predict gas adsorption capacity based on the material characterization model.Based on the slit-pore model to represent the gas properties under confinement,the theoretical procedure may help minimize experimental efforts in material synthesis and can be used for both process design and materials discovery.

2.Samples and Experimental Routine

Natural gas is a mixture of low molecular weighthydrocarbons with CH4as its major component.The storage capacity of natural gas is often calibrated with CH4adsorption measurements.In this work,we used three activated-carbon samples,labeled as AC1,AC2 and AC3,all from Fujian Yuanli Active Carbon Co.,Ltd.Those carbon samples are degassed at10−5kPa and 623 K prior to gas adsorption experiments.The adsorption capacities of these samples for pure CH4and pure CO2at 298 K are measured using Hiden IGA-2 with maximum maintain time of 0.5 h for equilibrium at each pressure.Adsorption isotherms are obtained within the pressure range from 0.2 MPa to 2 MPa.More adsorption isotherms,corresponding to samples AC4～AC7(A,B,C and Vulcan),are available from the literature[20].

3.Molecular Model and Numerical Procedure

3.1.Molecular model

To simulate gas adsorption in activated carbon,we use the slit-pore model for the adsorbent and the Lennard–Jones(LJ)model for gas molecules.The diameters of gas molecules(σff)are 0.364 and 0.381 nm,and the potential parameters(εff)are 236.15 and 148.10 K for CO2and CH4,respectively[21].As CO2molecules possess significant quadruples[22],the LJ parameters are fitted with the vapor–liquid coexistent densities at 298 K using the MBWR equation of state[23].Inside the slit pore,each gas molecule experiences an external potential represented by the Steele 10-4-3 model[24].The parameters for describing the gas–solid interactions are determined by the Lorentz–Berthelot rules[25].

3.2.Adsorption integral equation(AIE)

The adsorption integral equation(AIE)relates the overall gas adsorption amount of an amorphous material to that of the model slit pores and the pore-size distribution function[26]:

where L denotes the overall adsorption isotherm;v represents the kernel matrix;Pjis the gas pressure for the jthexperimental data point;f stands for the normalized pore-size distribution function.Typically,the pore-size distribution function has a hypothetical form(the B-spline function[27]).

In numerical implementation of AIE,Eq.(1)can be casted into the matrix form,L=A f,where A is the operator after the discretization of AIE.Using the rectangle discretization method[28],we can calculate A through A= ΔH ·v,where ΔH is the step length for the change in the pore width.Alternatively,the integration in AIE can be evaluated with the trapezoid method or the Simpson method.

To determine the adjustable parameters in the B-spline function,we minimize the objective function that is defined as the square deviation of the experimental and theoretical results for the gas adsorption amount:

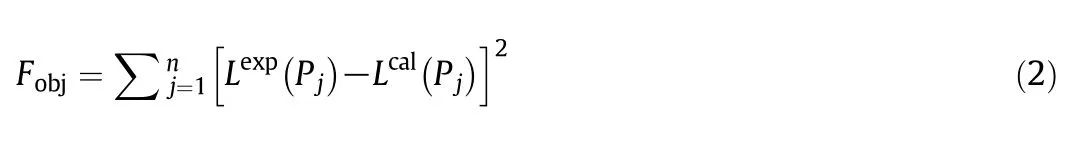
Although the overall adsorption isotherm is projected into an operator equation,which takes the linear least square form,we still have a non-linear optimization problem.The size of the kernel matrix is flexible,without limitations induced by variable dependence,namely the distribution value of each pore width is effective even the matrix is in underdetermined.

With the pore-size distribution function,we can calculate the average deviation of the experimental isotherm Lexpfrom the corresponding results from Eq.(1),Lcal,

where n is the number of experimental points in the adsorption measurements.

3.3.Density functionals

The classical density functional theory(DFT)has been recognized as being more rigorous than the BET method to describe gas adsorption isotherms[29,30].However,the performance of DFT calculations is highly dependent on the selection of the free-energy functional[31],which connects thermodynamic properties with the inhomogeneous distribution of the gas molecules inside the pore(viz.,density profiles).The free-energy functional typically includes two parts,an ideal-gas contribution and excess arising from intermolecular interactions.Whereas the former is exactly known,the excess contribution can only be approximated for most systems of practical concern.

For systems containing simple gas molecules like CH4or CO2,the excess free-energy functional can be divided into a hard-sphere contribution to account for intermolecular repulsions and a perturbation for describing van der Waals attractions[32].The modified fundamental measure theory(MFMT)[33]provides an accurate representation of the hard-sphere free energy.From a practical perspective,the main issue is thus on the accuracy of the attraction part of the excess Helmholtz energy.Toward that end,the mean- field approximation(MFA)represents a common choice.Like the van der Waals equation of state,MFA provides only qualitative predictions or at most semiquantitative for most practical applications.In this work,we consider three additional versions of DFT methods recently proposed in this literature.For convenience,these functionals are labeled as MFA[34],WDA-Yu[7],WDA-Liu[8]and FMSA[6].Brie fly,these excess Helmholtz free energy functionals are given by

MFA:

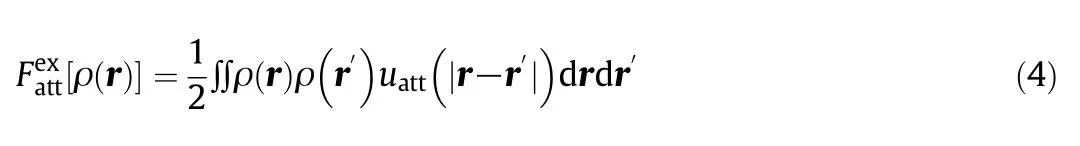
where r stands for molecular position;uattis the attractive component of the LJ pair potential(uLJ)defined according to the Barker–Henderson(BH)theory for the bulk system:

WDA:

The mean- field functional in Eq.(6),FMFA[ρ(r)],is the same as that from Eq.(4);¯ρ（r）stands for the weighted density profile;ϕcoris the Helmholtz free energy density induced by correlation interaction.In the version of non-local DFT proposed by Yu[7],the excess Helmholtz energy density is volumetric as given by Eq.(8).For the functional proposed by Liu et al.[8],designated as WDA-Liu,the excess Helmholtz energy density per molecule is given by

where,β=1/(kBT),T isthe absolute temperature;ρbis bulk density;V is the system volume.Different from the original version of DFT proposed by Yu[7],we used the excess Helmholtz free energy for bulk LJ fluids()from the MBWR equation of state[23].The excess Helmholtz free energy for hard-sphere fluid in the bulk system()is calculated from the Carnahan–Starling equation of state[35].

Tang and Wu[6]indicated that the LJ potential could be reproduced analytically by a double-Yukawa potential.Based on the first-order mean-spherical approximation(FMSA)[36],we are able to obtain the first and the second-order direct correlation functions(and.Subsequently,the excess Helmholtz free energy functional due to van der Waals' attraction can be determined through functional expansion:FMSA:

Whereas the numerical performance of the aforementioned functionals has been carefully examined before[37,38],we are not aware of any previous publication to calibrate their applications to materials characterization.In this work,we attempt to incorporate these functionals into conventional mathematical procedures for the analysis of pore-size distributions and test their performance to predictgas adsorption capacity.We hope that the numerical procedure will help close the gap between materials characterization and rational design and selection for targeted applications.

3.4.Grand canonical Monte Carlo(GCMC)

The GCMC molecular simulation was executed with Towhee 7.0.4[39].The input chemical potential,μLJ,can be related to the bulk temperature and pressure from the MBWR equation of state.The force field for gas molecules is based on the OPLS-AA force field with Towhee_ff Version 13[40].Each simulation run consists of 106Monte Carlo steps including particle insertion,deletion and displacement in both equilibrium and production stages.The parallel computation was implemented on the platform of Python packages to reduce the computational cost[41].

4.Results and Discussions

4.1.Calibration with the slit-pore model

We first calculated the equilibrium density profiles of gas molecules in slitpores and the average density throughρa=((z)d z)/H,where H is the pore width.The Gibbs excess adsorption is related to the difference between the average density inside the pore and that in the bulk,v=ρa−ρb.

Fig.1.CO2 adsorption in a single slit pore at 298 K with the pore width H=1.6 nm(a),2.1 nm(b)and 2.6 nm(c).Different versions of the classical DFT method are explained in the main text.

Fig.1 presents the theoretical results from GCMC simulation and from four versions of DFT discussed above.Given a molecular model,GCMC results are exact and thus provide a numerical basis to validate the accuracy of different DFT methods.Fig.1 indicates that two WDA methods,especially WDA-Yu,predict most accurate CO2adsorption isotherms in comparison with the GCMC data.Significant errors were found in both MFA and FMSA.MFA underestimates the adsorption capacity suggesting that correlation effects in general favor stronger gas adsorption.

Fig.2 shows kernels constructed from different versions of DFT for CO2adsorption isotherms over a broad range of pressure(0.2～2.0 MPa).The theoretical results were obtained for slit pores with the pore width varying from 0.65 nm to 5.00 nm.Compared with the GCMC data,MFA underestimates the adsorption isotherm over the entire range ofthe pore width considered in this work,By contrast,predictions from WDA-Yu are accurate at all conditions.

Fig.3 presents the CH4adsorption isotherms in individual slit pores predicted by the four versions of the DFT methods in comparison with GCMC data.Whereas the results from WDA-Yu and WDA-Liu are close to each other and both are in good agreement with GCMC data,discrepancies are noticeable for both MFA and FMSA predictions.As the pore width increases,the difference among the four DFT methods diminishes gradually,and all agree with GCMC reasonably well.

Fig.4 shows the kernels for CH4adsorption isotherms in slit pores over a broad range of the pore widths and pressures.Here,different panels correspond to results calculated from four DFT methods and from GCMC simulation.The CH4kernels from different theoretical procedures have a similar form and may have little effect when the local gas density is close to the bulk value.At 298 K,CH4is way beyond its critical temperature,but CO2is near its critical temperature.As a result,the MFA predictions for CO2adsorption are apparently less accurate than those for CH4in comparison with GCMC data[37].By contrast,the WDA-Yu method compares well with the GCMC results for both systems.

To construct an effective kernel for porous analysis,we use the local adsorption isotherms in a series of slit pores.The kernel is crucial for both the numerical solution of AIE and adsorption capacity prediction.Apparently,the required kernels are either hill-like[20](Figs.2 and 4)or slope-like showing a monotonically declining surface[42].For a specific material,the kernel shape is dependent on the target range of the pore width.The existing analysis techniques for kernel construction are diverse,including backward error analysis in term of the theoretical error bound scale[43],the kernel-size analysis with different ratios of rows and columns in the kernel matrix[44],as well as the smoothness comparison of the surface[18].Although the kernel is typically constructed based on certain prior heterogeneity hypothesis of the solid surface,the assumptions may have remarkable influence on pore characterization results[44].The effective part in the kernel is hard to quantitatively distinguish after the exploration of the minimum pore width probed by gas molecules[25].According to the statistic distributed properties,we propose the pore width interval between 0.65 and 2.30 nm as the feature pore width range(FPWR).The range of pore sizes corresponds to the major part of the peak on the surface(Figs.2 and 4),rather than～100 nm scale recommended by IUPAC.Compared with FPWR,the distribution value corresponding to the rest part of the PSD has less physical meaning because the reflection of porous structure plays a compensate role in numerical fitting of adsorption isotherms.

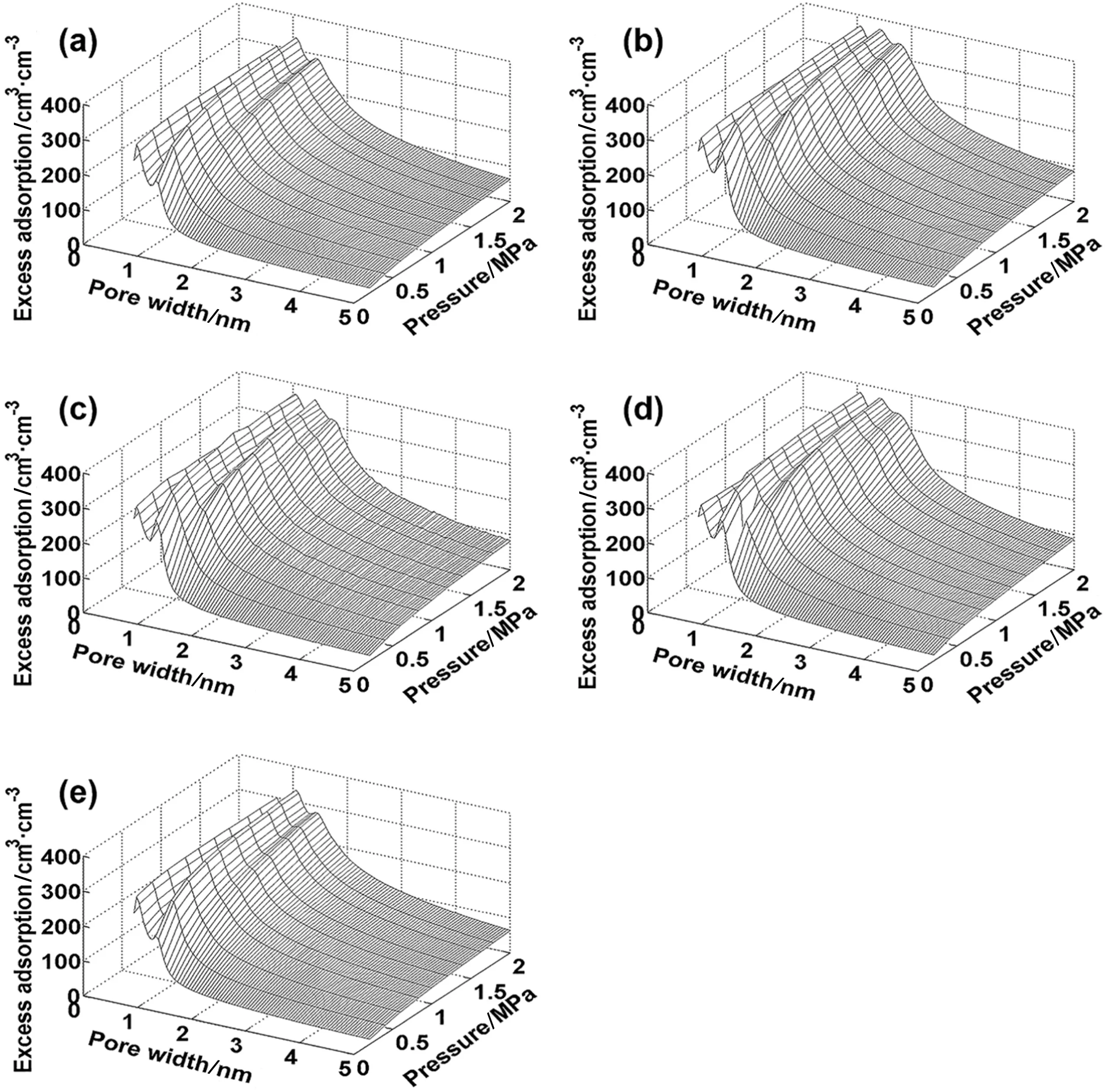
Fig.2.Kernel of CO2 adsorption calculated from different computational methods.(a)MFA,(b)WDA-Yu,(c)GCMC;(d)WDA-Liu;(e)FMSA.

Fig.3.CH4 adsorption in a single slit pore at 298 K with the pore width=1.6 nm(a),2.1 nm(b)and 2.6 nm(c).

Fig.4.Kernel of CH4 adsorption calculated from different computational methods.(a):MFA,(b):WDA-Yu,(c):GCMC;(d):WDA-Liu;(e):FMSA.

Table 1 Average deviation(%)on fitting CO2 isotherms

DFT is able to efficiently yield a smooth curve for the local isotherm in individual slit pores[37].The computational cost for kernel construction can be further reduced by numerical interpolation of the local isotherm.The deficiency in using the GCMC method for pore-size analysis is not only due to the computational time for calculating local adsorption isotherms in individual single-slit pores,but also due to the lack of mathematics trick that can be adopted for construction of the required kernel with fluctuated surfaces.

4.2.Pore-size analysis

Fig.5.The pore size distribution(PSD)of seven samples obtained from different computational methods.Panels(a)to(g)correspond to carbon samples AC1 to AC7,respectively.

In order to re flect the porous structure of activated carbon,we constructed the pore-size distribution(PSD)model for several representative samples by fitting the adsorption isotherm with AIE[45].The average fitting deviation can be treated as an important criterion in forward error analysis.The PSD analysis required from fitting N2isotherm at 77 K has been proved unreliable because small pores are impenetrable by gas molecules at low temperature,leading to underestimation of the probed PSD of samples[46].Pore-size analysis with CO2isotherm at 298 K obviates some of these issues[20].

According to the forward erroranalysis,the performance of different methodologies is compared with their average deviations in experimental isotherm fitting.In numerical implementation,we discretized AIE using the trapezoid method.The average deviation between experimental CO2isotherms for seven activated carbon samples and the fitted isotherms with the WDA-Yu functional and the related standard deviations are 90.0%and 91.2%,respectively,much smaller than those from MFA calculations(Table 1).The good fitting implies that the WDA-Yu functional is sufficiently accurate for the pore-size analysis.

In the following,we use only the WDA-Yu functional for the calibration of CO2isotherm fitting.It should be noted that the numerical solution of AIE is also affected by the discretization methods.With the WDA-Yu functional for kernel building,we further compare the average deviation in CO2isotherm fitting for seven activated carbon samples using three discretization methods,viz.,trapezoid rule,rectangle and Simpson methods.The numerical deviations are 1.08,5.36 and 8.68%;and their standard deviations are 2.3,13.7 and 22.4,respectively.Notably,the trapezoid method is the most suitable for discretization of AIE.

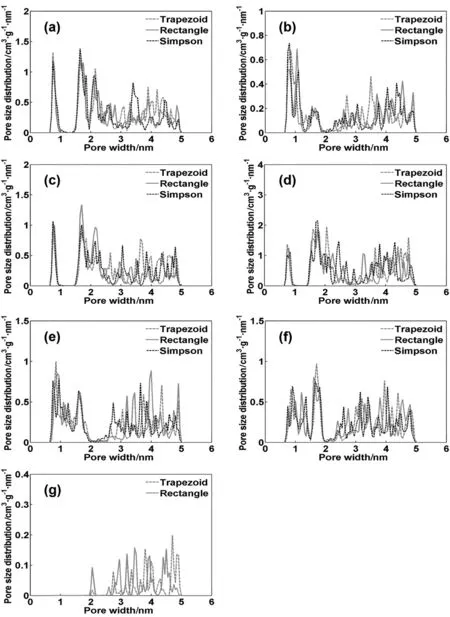
Fig.6.The pore size distribution(PSD)of seven samples obtained from different discretization methods.Panels(a)to(g)correspond to carbon samples AC1 to AC7,respectively.For AC7,the results from the Simpson method are omitted due to large deviation in isotherm fitting.

Figs.5 and 6 show that the FPWR part in PSD exhibits a smooth form,less sensitive to the adopted numerical procedure and thus is more representative for pore-size characterization.While different theoretical methods predict remarkably different PSDs for samples within the pore size ranging from 0.65 nm to 5.00 nm(ΔH=0.05 nm),the distribution value within FPWR appears close to each other(Fig.5).Moreover,the FPWR parts are less affected by the discretization methods,while the rest of PSD seems sensitive to the adopted theoretical procedures(Fig.6).

4.3.Optimal numerical procedure

The representativeness of the PSD function obtained from different theoretical methods can also be validated with their predictive capability for gas adsorption[20].The PSD model can be used to calculate CH4adsorption in different adsorbents discussed above at arbitrary thermodynamic conditions.Table 2 presents the average deviations between experimental and theoretical isotherms.The standard deviation for WDA-Yu,FMSA,MFA,WDA-Liu and GCMC are 3.2,5.8,30.0,3.3 and 2.7%,respectively.Among different DFT methods,the WDA-Yu functional yields the smallest mean and standard deviations.The theoretical procedure is able to provide a faithful representation of the PSD function and thus promising for large-scale screening according to the pore-size analysis of carbon porous materials.

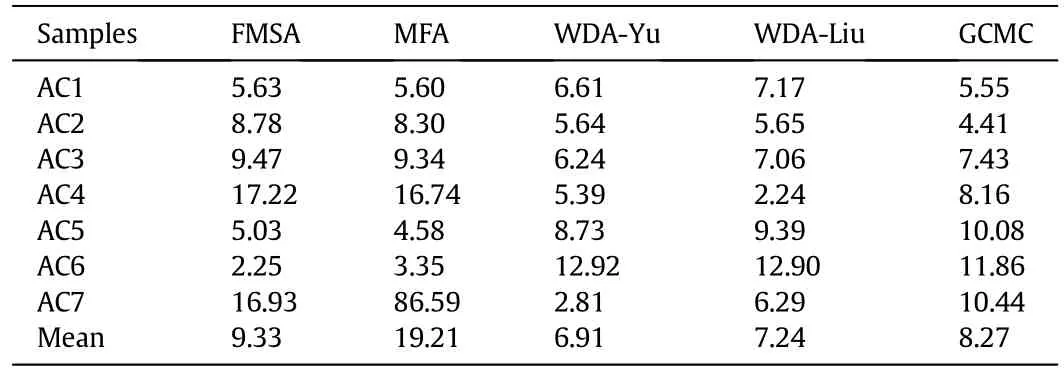
Table 2 Average deviation(%)of CH4 adsorption capacity predicted from different theoretical methods

A similar procedure has been used to validate the discretization method for AIE.Table 3 shows that the trapezoid method gives the smallest mean on predictive deviation for the seven carbon samples.The standard deviations of trapezoid,rectangle and Simpson discretization methods are 3.2,7.3 and 15.6%,respectively.If the largest deviation for AC7 is omitted,the mean deviation values for the above methods are 7.59,8.44 and 7.82%,respectively.The corresponding standard deviations are 2.9,2.8 and 2.9%,suggesting rather limited effect of the discretization method.

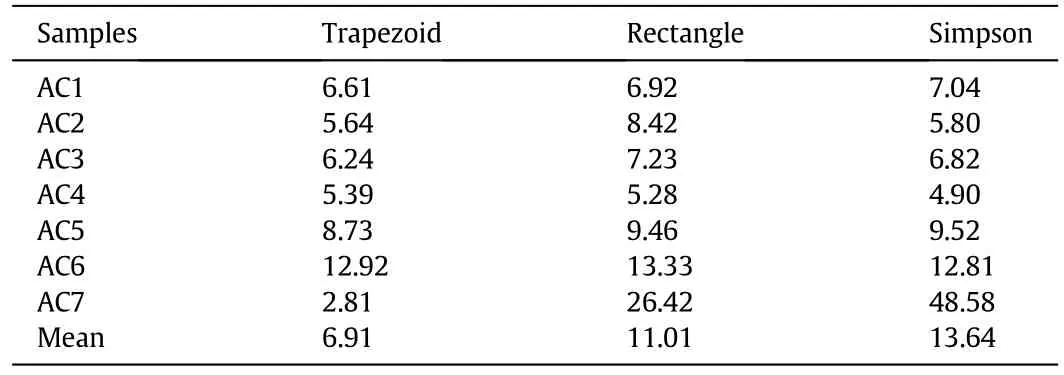
Table 3 Average deviation(%)of CH4 adsorption capacity predicted from different discretization methods

We can verify the faithfulness of FPWR in PSD from theoretical predictions of gas adsorption as well.Understandably,different theoretical methods lead to different pore size distributions in FPWR.Likewise,a similar form of FPWR leads to similar predictions.The details in FPWR of required PSD are truly important for the pore-size analysis as well as for the predictive calculation of adsorption capacity.As a preliminary hypothesis,the interval of FPWR is still blurry,which might be fixed when more samples are available.

5.Conclusions

In this paper,we discussed the accuracy and reliability of several theoretical procedures for the analysis of gas adsorption in various porous carbons.With the predictive capability as a benchmark,we show that the weighted-density approximation by Yu[6],here referred to as WDA-Yu,in combination with the trapezoid discretization ofthe adsorption integral equation(AIE),yields more faithful representation of the pore-size distribution(PSD)of amorphous carbon materials.The entire range of pore width can be divided into two parts,the feature pore width range(FPWR)with pore width approximately ranging from 0.65 to 2.30 nm and the compensate part.The distribution in FPWR is proved to be more representative for the analysis of activated carbon samples.The theoretical procedure presented in this work can be directly applied to characterization of other amorphous porous materials and for quantitative predictions of methane adsorption capacity based on PSD.

Acknowledgements

We give thanks to Professor Songlin Zuo in Nanjing Forestry University,Professor Xianlun Deng and Associate Professor Haitao Huang in National Engineering and Technology Research Center of Forest Chemistry Industry,China,for their kind help in review advices and activated carbon samples characterization.We also feel gratitude for Dr.Jia Fu,Dr.Yun Tian and Dr.Cheng Lian atthe University of California,Riverside for their constructive discussions,isotherm fitting and DFT codes.This work is implemented on the super computational center of Qingdao Institute of Bioenergy and Bioprocess Technology,Chinese Academy of Sciences.

[1]M.E.Casco,M.Martínez-Escandell,K.Kaneko,J.Silvestre-Albero,F.Rodríguez-Reinoso,Very high methane uptake on activated carbons prepared from mesophase pitch:a compromise between microporosity and bulk density,Carbon 93(2015)11–21.

[2]M.E.Casco,M.Martínez-Escandell,E.Gadea-Ramos,K.Kaneko,J.Silvestre-Albero,F.Rodríguez-Reinoso,High-pressure methane storage in porous materials:are carbon materials in the pole position?Chem.Mater.27(3)(2015)959–964.

[3]D.Cao,J.Wu,Modeling the selectivity of activated carbons for efficient separation of hydrogen and carbon dioxide,Carbon 43(7)(2005)1364–1370.

[4]G.Han,X.Wang,Investigation on characteristics of liquid self-diffusion in slit nanopores using simple quasicrystal model of liquid,Chin.J.Chem.Eng.23(6)(2015)897–904.

[5]M.Thommes,K.Cychosz,Physical adsorption characterization of nanoporous materials:progress and challenges,Adsorption 20(2)(2014)233–250.

[6]Y.Tang,J.Wu,Modeling inhomogeneous van der Waals fluids using an analytical direct correlation function,Phys.Rev.E 70(1)(2004)11201.

[7]Y.Yu,A novel weighted density functional theory for adsorption, fluid–solid interfacial tension,and disjoining properties of simple liquid films on planar solid surfaces,J.Chem.Phys.131(2)(2009)24704.

[8]Y.Liu,H.Liu,Y.Hu,J.Jiang,Density functional theory for adsorption of gas mixtures in metal-organic frameworks,J.Phys.Chem.B 114(8)(2010)2820–2827.

[9]M.Zeng,Y.Tang,J.Mi,C.Zhong,Improved direct correlation function for density functional theory analysis of pore size distributions,J.Phys.Chem.C 113(40)(2009)17428–17436.

[10]L.A.Mitchell,B.J.Schindler,G.Das,M.C.dos Ramos,C.McCabe,P.T.Cummings,M.D.LeVan,Prediction of n-alkane adsorption on activated carbon using the SAFT-FMTDFT approach,J.Phys.Chem.C 119(3)(2015)1457–1463.

[11]G.Shen,X.Lu,X.Ji,Modeling of molecular gas adsorption isotherms on porous materials with hybrid PC-SAFT-DFT,Fluid Phase Equilib.382(2014)116–126.

[12]Z.Li,Z.Jin,A.Firoozabadi,Phase behavior and adsorption of pure substances and mixtures and characterization in nanopore structures by density functional theory,SPE J.19(6)(2014)1096–1109.

[13]S.Patchkovskii,T.Heine,Quantized liquid density-functional theory for hydrogen adsorption in nanoporous materials,Phys.Rev.E 80(3)(2009)31603.

[14]J.Jagiello,J.P.Olivier,2D-NLDFT adsorption models for carbon slit-shaped pores with surface energetical heterogeneity and geometrical corrugation,Carbon 55(2013)70–80.

[15]J.Jagiello,J.P.Olivier,Carbon slit pore model incorporating surface energetical heterogeneity and geometrical corrugation,Adsorption 19(2)(2013)777–783.

[16]B.Peng,Y.Yu,A density functional theory for Lennard–Jones fluids in cylindrical pores and its applications to adsorption of nitrogen on MCM-41 materials,Langmuir 24(21)(2008)12431–12439.

[17]B.Peng,Y.Yu,A density functional theory with a mean- field weight function:applications to surface tension,adsorption,and phase transition of a Lennard–Jones fluid in a slit-like pore,J.Phys.Chem.B 112(48)(2008)15407–15416.

[18]J.Landers,G.Y.Gor,A.V.Neimark,Density functional theory methods for characterization of porous materials,Colloids Surf.A Physicochem.Eng.Asp.437(2013)3–32.

[19]G.Y.Gor,M.Thommes,K.A.Cychosz,A.V.Neimark,Quenched solid density functional theory method for characterization of mesoporous carbons by nitrogen adsorption,Carbon 50(4)(2012)1583–1590.

[20]M.Sweatman,N.Quirke,Characterization of porous materials by gas adsorption at ambienttemperatures and high pressure,J.Phys.Chem.B 105(7)(2001)1403–1411.

[21]X.Shao,Z.Feng,R.Xue,C.Ma,W.Wang,X.Peng,D.Cao,Adsorption of CO2,CH4,CO2/N2and CO2/CH4in novel activated carbon beads:preparation,measurements and simulation,AIChE J.57(11)(2011)3042–3051.

[22]T.Ihara,T.Furusato,S.Kameda,T.Kiyan,S.Katsuki,M.Hara,H.Akiyama,Initiation mechanism of a positive streamer in pressurized carbon dioxide up to liquid and supercritical phases with nanosecond pulsed voltages,J.Phys.D.Appl.Phys.45(7)(2012)75204.

[23]J.Johnson,J.Zollweg,K.E.Gubbins,The Lennard–Jones equation of state revisited,Mol.Phys.78(3)(1993)591–618.

[24]D.D.Do,Adsorption analysis:equilibria and kinetics,Imperial College Press,London,1998.

[25]C.Lastoskie,K.E.Gubbins,N.Quirke,Pore size heterogeneity and the carbon slit pore:a density functional theory model,Langmuir 9(10)(1993)2693–2702.

[26]K.Wang,D.D.Do,Characterizing the micropore size distribution of activated carbon using equilibrium data of many adsorbates at various temperatures,Langmuir 13(23)(1997)6226–6233.

[27]J.Jagiello,Stable numerical solution of the adsorption integral equation using splines,Langmuir 10(8)(1994)2778–2785.

[28]X.Shao,X.Zhang,W.Wang,Comparison of density functional theory and molecular simulation methods for pore size distribution of mesoporous materials,Acta Phys.-Chim.Sin.19(6)(2003)538–542.

[29]J.Wu,Variational methods in molecular modeling,Springer,Singapore,2017.

[30]J.Wu,Density functional theory for chemical engineering:from capillarity to soft materials,52(3)(2006)1169–1193.

[31]Y.Tian,J.Wu,Differential heat of adsorption and isosteres,Langmuir 33(4)(2017)996–1003.

[32]Y.Liu,Application of density functional theory in MOF material and DNA denaturation(Ph.D.Thesis)East China University of Science Technology,China,2012.

[33]Y.Yu,J.Wu,Structures of hard-sphere fluids from a modified fundamental-measure theory,J.Chem.Phys.117(22)(2002)10156–10164.

[34]P.I.Ravikovitch,Characterization of nanoporous materials by gas adsorption and density-functional theory(Ph.D.Thesis)Yale University,United States,1998.

[35]N.F.Carnahan,K.E.Starling,Equation of state for nonattracting rigid spheres,J.Chem.Phys.51(51)(1969)635–636.

[36]Y.Tang,Z.Tong,C.Y.Lu,Analytical equation of state based on the Ornstein–Zernike equation,Fluid Phase Equilib.134(1–2)(1997)21–42.

[37]J.Fu,Y.Liu,Y.Tian,J.Wu,Density functional methods for fast screening of metal-organic frameworks for hydrogen storage,J.Phys.Chem.C 119(10)(2015)5374–5385.

[38]J.Fu,Y.Tian,J.Wu,Classical density functional theory for methane adsorption in metal-organic framework materials,AIChE J.61(9)(2015)3012–3021.

[39]M.G.Martin,MCCCS towhee:a tool for Monte Carlo molecular simulation,Mol.Simul.39(14–15)(2013)1212–1222.

[40]J.Pranata,S.G.Wierschke,W.L.Jorgensen,OPLS potential functions for nucleotide bases.Relative association constants of hydrogen-bonded base pairs in chloroform,J.Am.Chem.Soc.113(8)(1991)2810–2819.

[41]L.Dalcín,R.Paz,M.Storti,J.D'Elía,MPI for python:performance improvements and MPI-2 extensions,J.Parallel Distrib.Comput.68(5)(2008)655–662.

[42]C.Sitprasert,Z.Zhu,F.Wang,V.Rudolph,A multi-scale approach to the physical adsorption in slit pores,Chem.Eng.Sci.66(22)(2011)5447–5458.

[43]G.Wang,Y.Tian,J.Jiang,J.Wu,Multimodels computation for adsorption capacity of activated carbon,Adsorpt.Sci.Technol.(2017),https://doi.org/10.1177/0263617417705472.

[44]G.Davies,N.Seaton,V.Vassiliadis,Calculation of pore size distributions of activated carbons from adsorption isotherms,Langmuir 15(23)(1999)8235–8245.

[45]S.H.Madani,L.H.Diaz,M.J.Biggs,P.Pendleton,Uncertainty in pore size distribution derived from adsorption isotherms:II.Adsorption integral approach,Microporous Mesoporous Mater.214(2015)217–223.

[46]S.H.Madani,C.Hu,A.Silvestre-Albero,M.J.Biggs,F.Rodríguez-Reinoso,P.Pendleton,Pore size distributions derived from adsorption isotherms,immersion calorimetry,and isosteric heats:a comparative study,Carbon 96(2016)1106–1113.