Phase Space View of Ensem b les of Excited States
NAGYÁgnes
Departmentof TheoreticalPhysics,University of Debrecen,H-4002Debrecen,Hungary
1 Introduction
Density functional theory1is a ground state theory.It is valid for the lowest-energy state in each symmetry class2,3.The theory was fi rst rigorously generalized for excited states by Theophilou4.Itwas furher generalized by Gross,Oliveira and Kohn5.Themethod was used in several calculations6–12.The relativistic generalization of this formalism has also been done13.The optimized potentialmethod was also extended to ensembles of excited states14.Wemention by passing that theories fora singleexcited statealso exists14–21.An alternative theory,worth remarking,is time-dependent density functional theory22,23.
The ground-state density functional theory was formalized as ‘thermodynam ics’ by Ghosh,Berkow itz and Parr24.A phase–space distribution function f(r,p)was derived by maxim izing a phase–space Shannon information entropy subject to the conditions that f yields the density and the local kinetic energy density of the system. A local Maxwell-Boltzmann distribution function was resulted and the conceptof local temperaturewas introduced.This phase-space description resulted several applications25–29.Extensions of the formalism have also been provided30–40.A couple of years ago the local thermodynam ic formalism was extended to ensembles of excited states41and ensemble local temperature was defined.
Recently the ground-state theory has been revisited42.The local temperature of the Ghosh-Berkow itz-Parr theory was defined via the kinetic energy density.However,the kinetic energy density isnotuniquely defined.Usually the everywhere positive gradient form is applied,though any function that integrates to the true kinetic energy can do.Ithas recently been shown42that it is possible selecting the kinetic energy density so that the local temperaturebea constant for thewhole system under consideration.Moreover,it turned out that the kinetic energy density corresponding to the constant temperature,maximizes the information entropy.
The ensemble kinetic energy density isnotdefined uniquely either.In thispaper theensemble temperatureand kineticenergy density resulting themaximum phase-spaceinformationentropy are presented.The extremum is obtained by the constrained search of Levy and Lieb43,44.
The outline of this paper is as follows:In Section 2 the ensemble theory of excited states is summarized.In Section 3 the local thermodynam ic formalism of ensembles is reviewed41.The constrained search is applied in Section 4 to obtain the ensemble kinetic energy density giving the maximum phase-space information entropy.Section 5 is devoted to an illustrative example and discussion.
2 Ensem b le density functional theory for excited states
The Schrödinger equations of the HamiltonianˆH can be w ritten as


are theenergy eigenvalues.Theensembleenergy isdefined as5

where w1≥w2≥...≥wM≥0.When theweighting factors are wi=1/M the eigenensemble of M states is obtained.It corresponds to the subspace theory of Theophilou4.
The generalized Hohenberg-Kohn-theorems for ensembles read as follows:
(i)The external potential v(r)is determined w ithin a trivial additive constant,by theensemble density n defined as

The ensemble functional E has its minimum at the correct ensemble density n.The variation principle leads to the Euler-equation:

The ensemble Kohn-Sham equationswere also derived:

is a functional of the ensemble density n.The ensemble exchange-correlation potential vxcis the functional derivative of theensembleexchange-correlation energy functional Exc.
3 A “therm odynam ical” view of ensem b les of excited states
Now,the thermodynamical transcription of ensembles is summarized41.Consider a system of N electrons in a local external potential v(r).The ensemble is specified by a phase-space distribution function f(r,p)thatsatisfies


m is the mass.The ensemble non-interacting kinetic energy density ts(r)integrates to the ensemble non-interacting kinetic energy Ekin

There exist several distribution functions that satisfy the marginal conditions(11)–(13).One can choose a distribution functionZmaxim izing the entropy
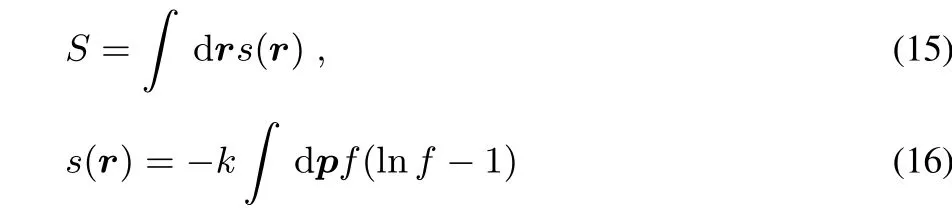
subjectto the constraintsofcorrectdensity(Eq.(11))and correct non-interacting kinetic energy(Eq.(13)).k is the Boltzmann constant.Themaximum entropy isa localMaxwell-Boltzmann distribution function

One can immediately see that itcan be rew ritten asan idealgas expression

where the local temperature T(r)is defined as

Then the Maxwell-Boltzmann distribution function takes the form
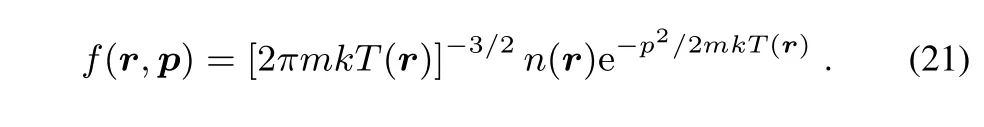
Substituting Eq.(21)into Eq.(15)we arrive at the well-known Sackur–TetroZde expression of the entropy:


Theeあectivepotential veあcanbe related to theensembleKohn-Sham potential.
4 Maxim um in fo rm ation en tropy w ith constrained search
In the previous section the information entropy was maxim ized w ith constraints(11)–(13).However,the ensemble kinetic energy density in Eq.(13)is not uniquely defined.Therefore the ensemble temperature in notunique either.Only the ensemble non-interacting kinetic energy Ekinin Eq.(14)is fixed.Any function that integrates to Ekinis a possible applicant for the ensemble non-interacting kinetic energy density,though functionseverywhere positive are preferred.
Now we select that ensemble temperature(or ensemble non-interacting kinetic energy density) that maxim izes information entropy.We are going tofind the phase-space distribution function f(r,p)thatsatisfies

The constrained search of Levy and Lieb43,44is applied.That is,the extremum is pursued in two steps.In the fi rst step the search is over all distribution functions that result a given ensemble temperature.In the second step the search isover all temperatures.We can immediatelly notice that the fi rststep has already been done in the previous section.The maximum information entropy after the fi rst step is given by the Sackur-Tetrode expression(22).In the second step we have tofind the ensemble temperature that makes the information entropy(22)w ith the constraint that

As the Lagrangemultiplierζis a constant,the temperature T of the ensemble is also a constant.Ithas the consequence that according to Eq.(18)the ensemble non-interacting kinetic energy density is proportional to the ensemble density n.Eqs.(27)and(28)lead to

The distribution function obtained by the constrained search isaMaxwell-Boltzmann distribution function

that is,Eq.(21)w ith the constantensemble temperature(33).
5 Discussion and illustrative exam p les
Take the linear harmonic oscillator as the fi rst the example.The potential is V=mω2x2,where m is themass andωis the frequency.The eigenvaluesare

where n=0,1,...is thequantum number.Becauseof thevirial theorem the kinetic energiesare

The ensemble kinetic energy is

Consequently the ensemble temperature is

In the subspace theory of Theophilou4w1=...=wM=1/M,theensemblekineticenergy and theensemble temperature take the form

Z,m and e and n=1,2,...are theatom ic number,theelectron mass,themagnitude of the electronic charge and the principal quantum number,respectively.In thesecond equality of Eq.(41)the virial theorem wasused.Then,theensemble kinetic energy is

where K is the numberof diあerentprincipalquantum numbers n.In the subspace theory of Theophilouwe have

wherewemakeuseof the factthatthedegeneracy ofa levelw ith the principalquantum number n is n2.Therefore the ensemble kinetic energy and the ensemble temperature have the form

One of our interesting results is that the ensemble temperature corresponding to the extremum phase-space information entropy is constant.This is true for any ensemble irrespective of the construction of the ensemble,that is,the weighting factors.Of course,the ensemble kinetic energy and consequently,the ensemble temperature w ill depend on the weighting factors,but itw illalwaysbe a constant.
The ensemble kinetic energy densitymaxim izing the phasespace information entropy is found to be proportional to the ensemble density.We emhasize here,that the know ledge of the ensemblekineticenergy density doesnotgiveusany information about the ensemble kinetic energy functional or its functional derivative.
This paper emhasizes the non-uniqueness of the local thermodynam ics and shows that the maximum entropy is attained if the ensemble temperature is constant.Theambiquity of the local thermodynam ics can also be considered an advantage from the pointof view of practicalapplications.One is free to select that particular ensemble local temperature(or ensemble kinetic energy density)that is themost suitable for the given application.It might happen that the constant ensemble temperature is themost favorable in certain cases.In other cases,another ensemble kinetic energy density and the corresponding temperature aremore beneficial.Itmeans that they can provide diあerentphysicalor chemical insight.
From information theoretic viewpoint the present theory has the significance that it is possible to selectan ensemble kinetic energy density that is proportional to the ensemble density.It means that the ensemble kinetic energy density has almost the same information as the ensemble density.There isa diあerence only in thenormalization:theensembledensity integrates to the numberofelectrons,whiletheensemblekineticenergydensity is normalized to theensemblekineticenergy.Thatis,themaximum entropy isattainedby theensemblekineticenergy densityhaving no new information in addition to theensemble density.
6 Conc lusions
In summary,we constructed ensembles of excited states and selected thatensemblekineticenergy density thatmaxim izesthe phase-space information entropy.The extremum was obtaned through the constrained search of Levy and Lieb.Thisensemble kinetic energy density is proportional to the ensemble density and the ensemble temperature is constant.
References
(1) Hohenberg,P.;Kohn,W.Phys.Rev.1964,136,B864.doi:10.1103/PhysRev.136.B864
(2) (a)Gunnarsson,O.;Lundqvist,B.I.Phys.Rev.B 1976,B13,4274.doi:10.1103/PhysRevB.13.4274(b)Gunnarsson,O.;Jonson M.;Lundqvist,B.I.Phys.Rev.B 1979,20,3136.doi:10.1103/PhysRevB.20.3136
(3) von Barth,U.Phys.Rev.A 1979,20,1693.doi:10.1103/PhysRevA.20.1693
(4) Theophilou,A.K.J.Phys.C 1978,C12,5419.doi:10.1088/0022-3719/12/24/013
(5) (a)Gross,E.K.U.;Oliveira,L.N.;Kohn,W.Phys.Rev.A 1988,37,2805.doi:10.1103/PhysRevA.37.2805(b)Gross,E.K.U.;Oliveira,L.N.;Kohn,W.Phys.Rev.A 1988,37,2809.doi:10.1103/PhysRevA.37.2809(c)Gross,E.K.U.;Oliveira,L.N.;Kohn,W.Phys.Rev.A 1988,37,2821.doi:10.1103/PhysRevA.37.2821
(6) Nagy,Á.Phys.Rev.A 1990,42,4388.doi:10.1103/PhysRevA.42.4388
(7) Nagy,Á.J.Phys.B 1991,24,4691.doi:10.1088/0953-4075/24/22/008
(8) Nagy,Á.;Andrejkovics,I.J.Phys.B 1994,27,233.doi:10.1088/0953-4075/27/2/002
(9) Nagy,Á.Int.J.Quantum.Chem.1995,56,225.doi:10.1002/qua.560560406
(10) Nagy,Á.J.Phys.B 1996,29,389.doi:10.1088/0953-4075/29/3/007
(11) Nagy,Á.Int.J.Quantum.Chem.1995,29(Suppl.),297.doi:10.1002/qua.560560833
(12) Nagy,Á.Adv.Quantum.Chem.1997,29,159.doi:10.1016/S0065-3276(08)60268-3
(13) Nagy,Á.Phys.Rev.A 1994,49,3074.doi:10.1103/PhysRevA.49.3074
(14) Nagy,Á.Int.J.Quantum.Chem.1998,69,247.doi:10.1002/(SICI)1097-461X(1998)69:3<247::AIDQUA4>3.0.CO;2-V
(15) Görling,A.Phys.Rev.A 1996,54,3912.doi:10.1103/PhysRevA.54.3912
(16) (a)Görling,A.;Levy,M.Phys.Rev.B 1993,47,13105.doi:10.1103/PhysRevB.47.13105(b)Görling,A.;Levy,M.Phys.Rev.A 1994,50,196.doi:10.1103/PhysRevA.50.196(c)Görling,A.;Levy,M.Int.J.Quantum.Chem.1995,29(Suppl.),93.doi:10.1002/qua.560560810
(17) Nagy,Á.Int.J.Quantum.Chem.1998,70,681.doi:10.1002/(SICI)1097-461X(1998)70:4/5<681::AIDQUA14>3.0.CO;2-5
(18) Levy,M.;Nagy,Á.Phys.Rev.Lett.1999,83,4361.doi:10.1103/PhysRevLett.83.4361
(19) Nagy,Á.;Levy,M.Phys.Rev.A 2001,63,052502.doi:10.1103/PhysRevA.63.052502
(20) Ayers,P.W.;Levy,M.;Nagy,Á.Phys.Rev.A 2012,85,042518.doi:10.1103/PhysRevA.85.042518
(21) Ayers,P.W.;Levy,M.;Nagy,Á.J.Chem.Phys.2015,143,191101.doi:10.1063/1.4934963
(22) Gross,E.U.K.;Dobson,J.F.;Petersilka,M.Density Functional Theory.In Topics in CurrentChemistry;Nalewajski,R.Ed.;Springer-Verlag:Heidelberg,Germany,1996;Vol.81,p.81.
(23) Casida,M.F.RecentAdvances in the Density FunctionalMethods.in RecentAdvances in ComputationalChemistry;Chong,D.P.Ed.;World Scientific:Singapore,1996;Vol.1,p.155.
(24) Ghosh,S.K.;Berkow itz,M.;Parr,R.G.Proc.Natl.Acad.Sci.USA 1984,81,8028.doi:10.1073/pnas.81.24.8028
(25) Ghosh S.K.;Parr,R.G.Phys.Rev.A 1986,34,785.doi:10.1103/PhysRevA.34.785
(26) Ghosh,S.K.;Berkow itz,M.J.Chem.Phys.1985,83,2976.doi:10.1063/1.449846
(27) Parr,R.G.;Rupnik,K.;Ghosh,S.K.Phys.Rev.Lett.1986,56,1555.doi:10.1103/PhysRevLett.56.1555
(28) Lee,C.;Parr,R.G.Phys.Rev.A 1987,35,2377.doi:10.1103/PhysRevA.35.2377
(29) Rong,C.Y.;Lu,T.;Chattaraj P.K.;Liu,S.B.Indian J.Chem.A 2014,53,970.
(30) Gadre,S.R.;Bendale,R.D.Int.J.Quant.Chem.1985,28,311.doi:10.1002/qua.560280212
(31) Gadre,S.R.;Sears,S.B.;Chakravorty,S.J.;Bendale,R.D.Phys.Rev.A 1985,32,2602.doi:10.1103/PhysRevA.32.2602
(32) Gadre,S.R.Phys.Rev.A 1984,30,620.doi:10.1103/PhysRevA.30.620
(33) Gadre,S.R.;Kulkani,S.A.;Shrivastava,I.H.Chem.Phys.Lett.1990,166,445.doi:10.1016/0009-2614(90)85058-K
(34) Gadre,S.R.;Bendale,R.D.;Gejii,S.P.Chem.Phys.Lett.1985,117,138.doi:10.1016/0009-2614(85)85222-2
(35) Nagy,Á.;Parr,R.G.Proc.Ind.Acad.Sci.Chem.Sci.1984,106,217.(36) Nagy,Á.;Parr,R.G.J.Mol.Struct.(Theochem)2000,501,101.doi:10.1016/S0166-1280(99)00418-2
(37) Nagy,Á.;Parr,R.G.Int.J.Quantum Chem.1996,58,323.doi:10.1002/(SICI)1097-461X(1996)58:4<323::AIDQUA1>3.0.CO;2
(38) Nagy,Á.Proc.Ind.Acad.Sci.(Chem.Sci)1994,106,251.
(39) Nagy,Á.ReviewsofModern Quantum Chemistry;Sen,K.D.Ed.;World Scientific:Singapore,2002;Vol.I,p.413.
(40) Nagy,Á.J.Mol.Struct.Theochem 2010,943,48.doi:10.1016/j.theochem.2009.10.010
(41) Nagy,Á.Indian J.Chem.A 2014,53,965.
(42) Nagy,Á.Int.J.Quantum Chem.2017,117,e5396.doi:10.1002/qua.25396
(43) Levy,M.Proc.Natl.Sci.USA 1979,76,6002.
(44) Lieb,H.Int.J.Quantum Chem.1982,24,243.doi:10.1002/qua.560240302

