Generalized Hirsh feld Partitioning w ith Orien ted and Prom o ted Proatom s

HEIDAR-ZADEH Farnaz, AYERS Paul W.

1 Department of Chem istry & Chem ical Biology; M cMaster University; Ham ilton, Ontario, L8P 4Z2, Canada.

2 Department of Inorganic and Physical Chemistry, Ghent University, Krijgslaan 281 (S3), 9000 Gent, Belgium.

3 Center for Molecular Modeling, Ghent University, Technologiepark 903, 9052 Zw ijnaarde, Belgium.

1 Motivation

Within the conceptual density functional theory (conceptual DFT) framework, chemical reactivity indicators are commonly defined as the derivatives of the ground-state energy and the grand potential w ith respect to the number of electrons,chem ical potential and external potential1–6. These global, local and nonlocal functions measure the sensitivity of a molecule to electron transfer and electrostatic interactions7–14. However, to pinpoint the molecule’s preferred reactive site in an electrophilic or a nucleophilic attack, it is common to partition the (non)local indictors among the constituent atoms and define the corresponding condensed reactivity indicators15–27. As atoms-in-molecules are not uniquely defined w ithin quantum mechanics, this requires selecting a method to decompose a molecule into atomic subsystems by distributing either the molecular orbitals28–35or the molecular electron density36–41.Here, we are interested in generalizing the Hirshfeld partitioning approaches to utilize non-spherical reference proatom densities.

In 1977, Hirshfeld proposed an approach for identifying atoms in a molecule based on the stockholder perspective40.Specifically, given the spherically-averaged densities of the isolated neutral reference atoms,, let the density of an atom in a molecule, ρA(r), be determ ined by the fraction of the molecular electron density, ρmol(r), that was “invested” by that reference atom, defined intuitively as

The density of the atom in a molecule (AIM) is then

and obviously the sum of the AIM densities is the molecular density, guaranteeing an exhaustive partitioning,

The reference-atom densities in Eq.(1) are commonly referred to as the proatom densities, and their sum is called the promolecular density,

While Hirshfeld presented the partitioning in Eq.(1) as a heuristic, Nalewajski and Parr provided a mathematical interpretation for it42–44. Their motivation was to define AIM to be as close as possible to isolated neutral atoms, and to maxim ize that closeness by m inim izing the Kullback-Leibler divergence between the density of AIM and the reference atoms,subject to the constraint in Eq.(3). The result of the Nalewajski-Parr variational formulation,

is the Hirshfeld AIM density, Eqs.(1)–(2). Once one realizes that the Hirshfeld partitioning tries to maxim ize the sim ilarity between the AIM densities and those of the neutral reference atoms in an information-theoretic sense, it is not surprising that Hirshfeld partitioning tends to systematically underestimate the magnitude of AIM charges (relative to other approaches like electrostatic potential fitting and natural population analysis)45.

To “improve” the Hirshfeld partitioning, one can use a different method to measure the dissim ilarity between the AIM density and the proatom density or one can use a different definition for the proatom46. Both techniques have been explored in the literature. There is a very broad class of dissim ilarity measures that retain the partitioning in Eq.(1)47–52,but the Kullback-Leibler divergence in particular has appealing mathematical properties53,54. It seems most effective, then, to change the definition of the proatom density. There are many attempts to do this in the literature, most (but not all55) of which are restricted to the spherically-symmetric proatom densities53,56–67.

To understand why aspherical proatoms are not commonly employed, suppose that one had aspherical proatom ic densities denoted by ρ0A;αA,βA,γA(r), where (αA, βA, γA) are the Euler angles controlling the orientation of proatom A. The best orientation for the proatom density is obtained by minim izing the information-theoretic divergence in Eq.(5) w ith respect to Euler angles

Because of the objective function’s complicated nonlinear dependence on the Euler angles, Eq.(7) is a difficult global optimization problem.

Moreover, it is not clear how one should choose the non-spherical densities. For example, for the sulfur atom,should one use a non-spherical density corresponding to the Cartesian p-orbitals, {pm}m=x,y,zor the ones defined by the(complex) spherical Harmonics, {Y1m}m=−1,0,+1? The answer almost certainly depends on the molecule that one is considering: one would expect to prefer a different representation for MgS (perhaps the spherical harmonics) and SO2(perhaps the Cartesian orbitals). In some molecules(perhaps SF6), the spherically averaged sulfur proatom density m ight be preferable.

In the next section, we w ill propose a method that avoids the problem of choosing an optimal orientation for the aspherical atomic densities. However the problem of global optimization,while perhaps somewhat reduced, w ill remain.

2 Orien ted p roatom s

2.1 Orien ted p roatom s in degenerate g round states

For simplicity, we w ill start by restricting ourselves to neutral proatoms, as in traditional Hirshfeld partitioning. The neutral atoms that can have non-spherical ground-state electron densities always have degenerate ground states. Let {Ψgdenote an orthonormal basis for the G-dimensional manifold of ground-state wave-functions defined by

The electron densities associated w ith pure (as opposed to mixed) ground states of this system have the form

where in the second line we have, for convenience, introduced the field operators.

In analogy to Eq.(7), we can consider the density expression of Eq.(10) as the proatom density and m inim ize the information loss w ith respect to the wave-function coefficients of each atom,

Both the objective function and the constraints are nonlinear in the wave-function coefficients, so this is again a (difficult)global optim ization problem. In addition, spherical proatom densities (which are not pure-state v-representable68,69) are excluded from Eq.(13).

Notice that an objective functions of the form

is positive definite. This motivates us to choose a new set of variables,

These constraints follow directly from the definition (16) and the normalization constraint on the wave-function, Eq.(9)70,71.The last constraint in Eq.(18) is especially important: w ithout this constraint the electron density in Eq.(17) can become negative.

To relax the requirement that the electron density corresponds to a pure state, we can relax the final equality in Eq.(18)70,71,

We can now rew rite Eq.(13) as the optim ization of a convex objective function subject to some constraints,

has negative eigenvalues. The constrained optim ization problem in Eq.(20), therefore, typically has many local m inima.Nonetheless, solution of Eq.(20) allows one to choose the best proatom density among the set of ensemble-state-representable ground state proatom densities.

2.2 Prom o ted p roatom s in quasi-degenerate g round states

To make contact w ith the valence-bond picture,it would be desirable to include promoted and ionized states of the reference proatoms. This is easily achieved using the previous approach because non-ground-state wave-functions can be included in Eq.(8),

Equation (20) still holds in this case, and a complete (but chemically unreasonable and computationally intractable)description would be obtained by including all possible wave-functions in Eq.(23). Sensible truncations are clearly required, perhaps by using sim ilar strategies to those one uses to select dom inant resonance structures in valence-bond approaches.

Notice that the optimization in Eq.(20) becomes tractable if all the transition densities are zero. i.e.,

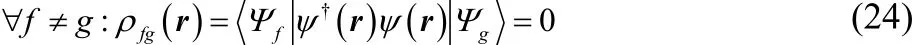
If the wave-functions are Slater determ inants, this is true for double-excitations. For exact eigenfunctions of the atoms, this is true when ΨfandΨgcorrespond to eigenstates of the number of electrons, the spin, or the spin-projection. (i.e.,different eigenfunctions of Nˆ, Sˆ2, or Sˆz) If we restrict ourselves to those eigenstates, then we can rew rite Eq.(20) as a convex optim ization problem w ith respect to linear constraints,

This formulation allows promoted proatoms, however because it does not allow one to adjust the orientation of the proatoms, the densities that are used in Eq.(25) should be spherically averaged. Nevertheless, Eq.(25) is a tractable convex optim ization, which can be solved using the same iterative strategies employed by the m inimal basis iterative stockholder analysis53.

3 Summ ary

We have developed a variational procedure, Eq.(20), which determines the optimal ground state proatom density in Hirshfeld partitioning. This procedure includes the traditional spherically-averaged neutral proatoms as a special case, but allows oriented and polarized proatoms to be used when that would allow the molecular electron density to be more closely approximated by the promolecular density. Unfortunately, the variational procedure is a convex optimization that is constrained by a non-convex inequality constraint, and so it w ill generally have many local minima. This procedure, then, is impractical except for very small molecules.

By including contributions from the wave-functions of excited and ionized states in Eq.(20), one can consider promoted and oriented proatoms. This variational procedure is also intractable in general, except when all the states under consideration have vanishing transition densities, Eq.(24). This condition is achieved if one considers only wave-functions corresponding to different eigenvalues for ˆN,2ˆS, or ˆzS,which allows one to generalize the Hirshfeld method to the variational principle in Eq.(25). This extended variational Hirshfeld framework requires the optimization of a convex objective function subject to linear constraints, and thus has a unique solution. We believe that the proatoms used in Eq.(25)provide a very prom ising direction for further generalizing Hirshfeld partitioning.

Acknow ledgm en t: This paper was motivated by a discussion we had w ith Prof. Randall (Randy) Dumont at McMaster University, and his remarkable ability to ask probing questions (about almost any topic) is appreciated and gratefully acknow ledged. Finally, we w ish to dedicate this paper to the memory of Robert (Bob) Parr: w ithout his inspiring scientific work (esp. Ref. 44) and exemplary scientific temperament, this paper could not have been w ritten.

References

(1) Parr, R. G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford UP: New York, NY, USA, 1989.

(2) Yang, W.; Cohen, A. J.; Proft, F. D.; Geerlings, P. J. Chem. Phys.2012, 136 (14), 144110. doi: 10.1063/1.3701562

(3) Geerlings, P.; De Proft, F.; Langenaeker, W. Chem. Rev. 2003, 103(5), 1793. doi: 10.1021/cr990029p

(4) Gázquez, J. L. J. Mex. Chem. Soc. 2008, 52, 3.

(5) Liu, S.-B. Acta Phys. -Chim. Sin. 2009, 25 (3), 590.doi: 10.3866/PKU.WHXB20090332

(6) Heidar-Zadeh, F.; M iranda-Quintana, R. A.; Verstraelen, T.;Bultinck, P.; Ayers, P. W. J. Chem. Theory Comp. 2016, 12 (12),5777. doi: 10.1021/acs.jctc.6b00494

(7) Heidar-Zadeh, F.; Richer, M.; Fias, S.; M iranda-Quintana, R. A.;Chan, M.; Franco-Perez, M.; Gonzalez-Espinoza, C. E.; Kim, T. D.;Lanssens, C.; Patel, A. H. G.; et al. Chem. Phys. Lett. 2016, 660, 307.doi: 10.1016/j.cplett.2016.07.039

(8) Geerlings, P.; De Proft, F. Phys. Chem. Chem. Phys. 2008, 10 (21),3028. doi: 10.1039/B717671F

(9) Fuentealba, P.; Parr, R. G. J. Chem. Phys. 1991, 94 (8), 5559.doi: 10.1063/1.460491

(10) Senet, P. J. Chem. Phys. 1996, 105 (15), 6471.doi: 10.1063/1.472498

(11) Franco-Pérez, M.; Ayers, P. W.; Gázquez, J. L.; Vela, A. J. Chem.Phys. 2015, 143 (24), 244117. doi: 10.1063/1.4938422

(12) Ayers, P. W.; Anderson, J. S. M.; Bartolotti, L. J. Int. J. Quantum Chem. 2005, 101 (5), 520. doi: 10.1002/qua.20307

(13) Echegaray, E.; Cardenas, C.; Rabi, S.; Rabi, N.; Lee, S.; Zadeh, F. H.;Toro-Labbe, A.; Anderson, J. S. M.; Ayers, P. W. J. Mol. Model.2013, 19 (7), 2779. doi: 10.1007/s00894-012-1637-3

(14) Echegaray, E.; Rabi, S.; Cardenas, C.; Zadeh, F. H.; Rabi, N.; Lee, S.;Anderson, J. S. M.; Toro-Labbe, A.; Ayers, P. W. J. Mol. Model.2014, 20, 2162. doi: 10.1007/s00894-014-2162-3

(15) Yang, W.; Mortier, W. J. J. Am. Chem. Soc. 1986, 108 (19), 5708.doi: 10.1021/ja00279a008

(16) Ayers, P. W.; Morrison, R. C.; Roy, R. K. J. Chem. Phys. 2002, 116(20), 8731. doi: 10.1063/1.1467338

(17) Bultinck, P.; Fias, S.; Van A lsenoy, C.; Ayers, P. W.; Carbó-Dorca,R. J. Chem. Phys. 2007, 127 (3), 034102. doi: 10.1063/1.2749518

(18) Echegaray, E.; Toro-Labbe, A.; Dikmenli, K.; Heidar-Zadeh, F.;Rabi, N.; Rabi, S.; Ayers, P. W.; Cardenas, C.; Parr, R. G.; Anderson,J. S. M. In Correlations in Condensed Matter under Extreme Conditions: A Tribute to Renato Pucci on the Occasion of His 70th Birthday; La Magna, A. Ed.; Springer International Publishing:Cham, Sw itzerland, 2017; p. 269.doi: 10.1007/978-3-319-53664-4_19

(19) Fuentealba, P.; Pérez, P.; Contreras, R. J. Chem. Phys. 2000, 113 (7),2544. doi: 10.1063/1.1305879

(20) Tiznado, W.; Chamorro, E.; Contreras, R.; Fuentealba, P. J. Phys.Chem. A 2005, 109 (14), 3220. doi: 10.1021/jp0450787

(21) Zadeh, F. H.; Fuentealba, P.; Cardenas, C.; Ayers, P. W. Phys. Chem.Chem. Phys. 2014, 16 (13), 6019. doi: 10.1039/c3cp52906a

(22) Rong, C.; Lu, T.; Liu, S. J. Chem. Phys. 2014, 140 (2), 024109.doi: 10.1063/1.4860969

(23) Morgenstern, A.; W ilson, T. R.; Eberhart, M. E. J. Phys. Chem. A 2017, 121 (22), 4341. doi: 10.1021/acs.jpca.7b00630

(24) Sablon, N.; Proft, F. D.; Ayers, P. W.; Geerlings, P. J. Chem. Phys.2007, 126 (22), 224108. doi: 10.1063/1.2736698

(25) Olah, J.; Van A lsenoy, C.; Sannigrahi, A. B. J. Phys. Chem. A 2002,106 (15), 3885. doi: 10.1021/jp014039h

(26) Liu, S. J. Chem. Phys. 2014, 141 (19), 194109.doi: 10.1063/1.4901898

(27) Zhou, X.-Y.; Rong, C. Y.; Lu, T.; Liu, S. B. Acta Phys. -Chim. Sin.2014, 30 (11), 2055. doi: 10.3866/PKU.WHXB201409193

(28) Mulliken, R. S. J. Chem. Phys. 1955, 23 (10), 1833.doi: 10.1063/1.1740588

(29) Mulliken, R. S. J. Chem. Phys. 1955, 23 (10), 1841.doi: 10.1063/1.1740589

(30) Mulliken, R. S. J. Chem. Phys. 1955, 23 (12), 2338.doi: 10.1063/1.1741876

(31) Mulliken, R. S. J. Chem. Phys. 1955, 23 (12), 2343.doi: 10.1063/1.1741877

(32) Löwdin, P.-O. Adv. Quantum Chem. 1970, 5, 185.doi: 10.1016/S0065-3276(08)60339-1

(33) Davidson, E. R. J. Chem. Phys. 1967, 46 (9), 3320.doi: 10.1063/1.1841219

(34) Reed, A. E.; Weinstock, R. B.; Weinhold, F. J. Chem. Phys. 1985,83 (2), 735. doi: 10.1063/1.449486

(35) Lu, W. C.; Wang, C. Z.; Schmidt, M. W.; Bytautas, L.; Ho, K. M.;Ruedenberg, K. J. Chem. Phys. 2004, 120 (6), 2629.doi: 10.1063/1.1638731

(36) Bader, R. F. W. Atoms in Molecules: A Quantum Theory;Clarendon: Oxford, UK, 1990.

(37) Heidarzadeh, F.; Shahbazian, S. Int. J. Quantum Chem. 2010, 111(12), 2788. doi: 10.1002/qua.22629

(38) Zadeh, F. H.; Shahbazian, S. Theor. Chem. Acc. 2010, 128 (2),175.doi: 10.1007/s00214-010-0811-x

(39) Morgenstern, A.; Morgenstern, C.; M iorelli, J.; W ilson, T.;Eberhart, M. E. Phys. Chem. Phys. Chem. 2016, 18 (7), 5638.doi: 10.1039/c5cp07852k

(40) Hirshfeld, F. L. Theor. Chim. Act. 1977, 44, 129.doi: 10.1007/BF00549096

(41) Guerra, C. F.; Handgraaf, J. W.; Baerends, E. J.; Bickelhaupt, F.M.J. Comput. Chem. 2004, 25 (2), 189. doi: 10.1002/jcc.10351

(42) Nalewajski, R. F.; Parr, R. G. Proc. Natl. Acad. Sci. 2000, 97,8879. doi: 10.1073/pnas.97.16.8879

(43) Nalewajski, R. F.; Parr, R. G. J. Phys. Chem. A 2001, 105 (31),7391. doi: 10.1021/jp004414q

(44) Parr, R. G.; Ayers, P. W.; Nalewajski, R. F. J. Phys. Chem. A 2005, 109 (17), 3957. doi: 10.1021/jp0404596

(45) Davidson, E. R.; Chakravorty, S. Theor. Chim. Acta 1992, 83 (5–6), 319. doi: 10.1007/bf01113058

(46) Heidar-Zadeh, F.; Ayers, P. W.; Verstraelen, T.; Vinogradov, I.;Vohringer-Martinez, E.; Bultinck, P. J. Phys. Chem. A subm itted,2017.

(47) Heidar-Zadeh, F.; Ayers, P. W.; Bultinck, P. J. Chem. Phys. 2014,141, 094103. doi: 10.1063/1.4894228

(48) Heidar-Zadeh, F.; Ayers, P. W. J. Chem. Phys. 2015, 142 (4),044107. doi: 10.1063/1.4905123

(49) Heidar-Zadeh, F.; Vinogradov, I.; Ayers, P. W. Theor. Chem. Acc.2017, 136 (4), 54. doi: 10.1007/s00214-017-2077-z

(50) Ayers, P. W. J. Chem. Phys. 2000, 113 (24), 10886. doi:10.1063/1.1327268

(51) Ayers, P. W. Theor. Chem. Acc. 2006, 115, 370.doi: 10.1007/s00214-006-0121-5

(52) Heidar-Zadeh, F.; Ayers, P. W. Theor. Chem. Acc. 2017, 136 (8),92. doi: 10.1007/s00214-017-2114-y

(53) Verstraelen, T.; Vandenbrande, S.; Heidar-Zadeh, F.;Vanduyfhuys, L.; Van Speybroeck, V.; Waroquier, M.; Ayers, P.W. J. Chem. Theory Comp. 2016, 12 (8), 3894. doi:10.1021/acs.jctc.6b00456

(54) Heidar-Zadeh, F. Variational Information-Theoretic Atoms-in-Molecules. Ph. D. Dissertation, M cMaster University,Canada, and Ghent University, Belgium, 2017.

(55) M isquitta, A. J.; Stone, A. J.; Fazeli, F. J. Chem. Theory Comp.2014, 10 (12), 5405. doi: 10.1021/ct5008444

(56) Verstraelen, T.; Ayers, P. W.; Van Speybroeck, V.; Waroquier, M.J. Chem. Theory Comp. 2013, 9 (5), 2221. doi:10.1021/ct4000923

(57) Bultinck, P.; Van Alsenoy, C.; Ayers, P. W.; Carbo-Dorca, R.J. Chem. Phys. 2007, 126 (14), 144111. doi: 10.1063/1.2715563

(58) Bultinck, P.; Ayers, P. W.; Fias, S.; Tiels, K.; Van Alsenoy, C.Chem. Phys. Lett. 2007, 444 (1−3), 205. doi:10.1016/j.cplett.2007.07.014

(59) Ghillem ijn, D.; Bultinck, P.; Van Neck, D.; Ayers, P. W. J.Comput. Chem. 2011, 32, 1561. doi: 10.1002/jcc.21734

(60) Manz, T. A.; Sholl, D. S. J. Chem. Theory Comp. 2010, 6 (8),2455. doi: 10.1021/ct100125x

(61) Manz, T. A.; Sholl, D. S. J. Chem. Theory Comp. 2012, 8 (8),2844. doi: 10.1021/ct3002199

(62) Lee, L. P.; Limas, N. G.; Cole, D. J.; Payne, M. C.; Skylaris, C.K.; Manz, T. A. J. Chem. Theory Comp. 2014, 10 (12), 5377.doi: 10.1021/ct500766v

(63) Limas, N. G.; Manz, T. A. RSC Adv. 2016, 6 (51), 45727.doi: 10.1039/c6ra05507a

(64) Manz, T. A.; Limas, N. G. RSC Adv. 2016, 6 (53), 47771.doi: 10.1039/c6ra04656h

(65) Lillestolen, T. C.; Wheatley, R. J. Chem. Commun. 2008, 45,5909. doi: 10.1039/b812691g

(66) Lillestolen, T. C.; Wheatley, R. J. J. Chem. Phys. 2009, 131,144101. doi: 10.1063/1.3243863

(67) Verstraelen, T.; Ayers, P. W.; Van Speybroeck, V.; Waroquier, M.Chem. Phys. Lett. 2012, 545, 138. doi:10.1016/j.cplett.2012.07.028

(68) Levy, M. Phys. Rev. A 1982, 26 (3), 1200.doi: 10.1103/PhysRevA.26.1200

(69) Lieb, E. H. Int. J. Quantum Chem. 1983, 24 (3), 243.doi: 10.1002/qua.560240302

(70) Ayers, P. W. Phys. Rev. A 2006, 73, 012513.doi: 10.1103/PhysRevA.73.012513

(71) Cardenas, C.; Ayers, P. W.; Cedillo, A. J. Chem. Phys. 2011, 134,174103. doi: 10.1063/1.3585610