Fukui函数和局域软度应用于亲电加成反应的区位选择性的研究
朱尊伟,杨巧凤,徐珍珍,,*,赵东霞,*,樊红军,杨忠志
1辽宁师范大学化学化工学院,辽宁 大连 116029
2中国科学院大连化学物理研究所,辽宁 大连 116029
1 In troduction
Electrophilic addition of an electrophile to alkenes is one of the most w idely studied electrophilic reactions1–9, as shown in Fig.1. The analysis of this sort of reactions has attracted great concern of both experimental and theoretical studies.Regioselectivity for the electrophilic addition has been shown tofollow the empirical Markovnikov’s rules10, the addition of an acidic proton to a double bond of an alkene yields a product where the proton is bound to the carbon atom bearing the largest number of hydrogen atoms when the substituent of alkene is electron-donating group. And when the substituent is electron-accepting group, the proton of acid favors to attack the carbon atom bearing the smallest number of hydrogen atoms,which calls the anti-Markovnikov’s rule. Many theoretical1–4,8and experimental5–7,9studies have focused on the regioselectivity of electrophilic addition to alkene all the while,such as, frontier molecular orbital (FMO) theory is sometimes used for explaining the regioselectivity of reaction8. Suresh and his coworkers have employed the molecular electrostatic potential to confirm the regioselectivity of Markovnikov reaction2. Recently, Yang, Ding and Zhao1have performed to use the frontier electron density of initial-state carbon atoms in molecular face theory (MFT) to estimate its regioselectivity: if the frontier electron density encoded on the Markovnikov carbon atom is larger than that of anti-Markovnikov, the reaction may be predicted to proceed on the Markovnikov route, and otherw ise it may prefer the anti-Markovnikov route.
The local hard-soft and acids-bases (HSAB) principle is an efficient method in conceptual density functional theory(CDFT) to predict the regio- and stereoselectivities of reactions, especially the corresponding softness matching in a local approach11–17for two or four or much more reactive points between two reactants. Li-Evans18proposed that for a hard reaction the site of m inimal Fukui function (FF) is preferred and for a soft reaction the site of maximal Fukui function is preferred. Gazquez and Mendez19stated that the reaction between two chemical species w ill not necessarily occur through their softest atoms, but through those sites whose local softness are close to each other. In this respect, Geerlings,Proft and Langenacker20suggested that local softness should be used as an intermolecular reactivity descriptor, whereas the FF is as an intramolecular one. Thus, the comparisons of the FF or condensed FF values for different systems are meaningless because they represent only the relative reactivity among different sites w ithin a molecule. Therefore, in order to rationalize the intermolecular reactivity, we have proposed a series of generalized reactivity descriptors21, including generalized Fukui function (GFF) and generalized local softness (GLS)22.
Recently,based on the generalized reactivity descriptors we have been successful to predict and to explain the regio-/stereoselectivities of Diels-Alder reactions22and the enzymatic catalyzed reactions of biological system21and to correlate their intermolecular reactivities of all reactions in terms of the atom-bond electronegativity equalization method(ABEEMσπ) model w ith the local HSAB principle at its generalized version. And we have obtained the results in good agreement w ith the experimentally observed outcomes.
In this paper, we w ill use the usual reactivity descriptors and the generalized one combined w ith the local HSAB principle to investigate the regioselectivities of the electrophilic additions of alkene including the hydrogen chloride and benzeneselenyl w ith unsymmetrical alkene and to rationalize their order of reaction rate constants by the ab initio method at the level of MP2/6-311++G(d,p) w ith the finite difference approximation(FDA) method and the ABEEMσπ model. It should be noted that the FDA method involves the three systems of N, N + 1,and N − 1 electrons, but ABEEMσπ model only involves one system of N electron.

Fig.1 The regioselectivities of electrophilic additions of hyd rogen ch loride to the substituted ethenes (R3 = H) and benzeneselenenyl brom ide to substituted styrenes (R1 = R2 = H), including M arkovnikov and anti-M arkovnikov p roducts.
2 Theo ry backg round
2.1 The reac tivity descrip to rs
Fukui function (FF) is one of the important reactivity descriptors in predicting the intramolecular reactivity in CDFT23,24. Parr and Yang defined the FF ()f r→ and local softness ()s r→25,26as:

whereis the electron density at, N is the number of electrons for a molecular system, μ is the chem ical potential,the negative of the electronegativity,is the external potential generated by the nuclei, S is the global softness.
2.2 The finite d ifference app roxim ation (FDA)
In the FDA method, according to the Eq.(1), the condensed FF of nucleophilic attack for systems w ith electron gain can be w ritten as

and the condensed FF of electrophilic attack for systems w ith electron donation can be expressed as

where qk(N + 1), qk(N), and qk(N − 1) stand for the partial charges on atom k in a molecule w ith N + 1, N, and N − 1 electrons at the same geometry stru→cture, respectively27.
A local softness descriptor s( r) is related to the FF via Eq.(2), so the condensed local softness is related to the condensed FF26through

where,andimply how global softness is redistributed among various atoms of the molecule by the condensed Fukui function. The global softness, S, can be given as24S = 1/I − A where I and A are the ionization potential and electron affinity,respectively. The first ionization potential I can be obtained by I = EN−1− ENand the electron affinity A by A = EN+1− ENw ith EN−1, EN, and EN+1denoting the total energies of the systems w ith N − 1, N, and N + 1 electrons, respectively. The quantities involved can be calculated by an ab initio method at high level of theory.
2.3 ABEEMσπ m odel
Based on the DFT and electronegativity equalization method(EEM)28–34, Yang and his coworkers have developed ABEEMσπ model35–45, which explicitly partitions a molecule into atom, chemical bond, and lone pair (lp) regions. In this model, the single bond consists of one σ region, where the center of the charge for σ bond is located on the position of the ratio of the covalent atomic radii of two bonded atom; the double bond consists of one σ region and four π regions, where center of the σ bond charge is sim ilar w ith the σ region of single bond and the π bond partial charges are placed above and below the double-bonded atoms at the covalent radii of the this double-bonded atoms perpendicular to the plane formed by the σ bond; and the center of charge and its orientation for the lp region is determ ined in terms of the chem ical surrounding.
In terms of the definition of electronegativity based on DFT,the effective electronegativity of a region a, χa, can be expressed as:

whereandare valence-state electronegativity and hardness of the region a, respectively. a and b denote two regions, including the atom or single bond σ or double bond σ and π or lone pairs regions. qa and qb are the partial charges of regions a and b, Ra,b denotes the distance between regions a and b, and k, 0.57, is an overall correction coefficient in this formalism22,35–47. The electronegativity equalization principle demands that the effective electronegativity of every region is equal to the overall electronegativity of the molecule, χmol:

For an arbitrary molecule partitioned into m regions, solving the Eq.(8) w ith the constraint Eq.(9) on its net charge, qmol, if the parametersandare known, we can obtain the charge of every region.

On the basis of the definition of the FF, we can express the FF of region a in our ABEEMσπ model as:

Hardness expressions for all the regions in a molecule like Eq.(11), altogether w ith the normalization condition of the FF, ∫f( r) dr = 1, can be also solved to directly and quickly give the molecular hardness, 2ηmol, and in particular, the condensed FF faof each region in the molecule if all parameters 2η*in Eq.(11) have been calibrated.
2.4 The generalized reac tivity desc rip to rs
The generalized Fukui function (GFF) fG(r) and the generalized local softness (GLS) sGhave been proposed and their definitions22are expressed as Eqs.(12) and (13):

where, the f(and s→) are local Fukui function (FF) and local softness, the usual reactivity descriptors, NMis the number of atoms for a molecular system, and S is the global softness. Obviously, according →to Eq.(12), the GFF fG(r→) is normalized to NMbecause f( r) is normalized to 1 for a molecule. And sG( r→) is normalized to NMS rather than S,which means that the global softness is the average of the generalized local softness sG( r→). Based on the definition of fG( r→), the reactivity descriptor→ of the site is not only dependant on its charge and f( r), but also related to the number of the atoms in the molecule, NM, where the detailed ratiocination has been represented in Ref. 22.
3 Com pu tational details
We investigated the electrophilic additions of hydrogen chloride to asymmetric alkenes and benzeneselenenyl bromide to substituted styrenes, as shown in Fig.1. The geometries of all reactants were optimized and obtained by the B3LYP/6-311+G(d,p) level of theory in Gaussian-0348. All optimized reactants were stationary points of potential energy surface after checking the frequencies at the same level of theory.
3.1 Calib ration of param eters χ* and 2η* fo r ABEEMσπ Model
According to Eq.(7) and Eq.(11), we have calibrated the parameters χ*and 2η*, through a regression and least-squares optimization procedure by dealing with some model molecules35.For all model molecules, ab initio Hartree-Fock MO calculations were performed w ith STO-3G basis sets in Gaussian 0348and then the partial charges of all the model molecules were obtained by the Mulliken population analysis.Then the charge distributions obtained for the model molecules were brought into Eqs.(7–9) in order to determine the parameters χ*and 2η*through a regression and least-squares optimization procedure22,35–38,46,47. The old types of parameters were obtained from our previous work37, and the new added types and parameters of χ*and 2η*are listed in Table 1.
For the calibration, the reason why we use the minimum STO-3G basis set is not due to its time-consuming but more importantly due to its physical significance. Ab initio calculation w ith a higher level of basis set can give more accurate prediction of energy and geometry, but can not give more suitable partial charges than lower level of basis set for practical use. This phenomenon comes from the fact that a diffuse basis function located on an atom may to some extent cover the regions of the other adjacent atoms leading to a somewhat overestimating population of this atom in the Mulliken population analysis. Derouane and coworkers49showed that the formal charges calculated w ith the 6-21 basis set are higher than those computed w ith the STO-3G basis set,and thus suggested STO-3G charges may be more reliable.W ilson and Ichikawa50and Torrent-Sucarrat and their coworkers51pointed out that the charge transfer between atoms in a molecule is overestimated when the polarization basis sets are used. Huzinaka et al.52and Jakalian et al.53, as well as our group47, had experienced that the use of higher level of basis sets overestimates the overlapping between their respective basis functions belonging to two atoms in a molecule. For example, if the 6-31G* basis set is used, the polarity of a molecule calculated by the partial charges is overestimated by 10%–15% than if the STO-3G basis set is used53. Therefore, in the calibration process of the parameters, STO-3G basis set has been used in the ab initio calculations for all the model molecules to obtain the partial charges from Mulliken population analysis.

Tab le 1 Parameters χ* and 2η* in ABEEMσπ M odel.
3.2 Calcu lation of Fukui func tion and local softness
Geerlings, Proft and Langenacker20suggested that local softness should be used as an intermolecular reactivity descriptor, whereas the FF is as an intramolecular one. Under the FDA method, via S = 1/(I − A), the global softness were obtained, where the first ionization potential I and the electron affinity A were calculated by ab initio method at MP2/6-311++G(d,p) level of theory. In terms of Eqs.(3) and(4), the condensed FFs of center atoms were calculated using the natural population analysis (NPA) at the MP2/6-311++G(d,p) level of theory, then obtained their local softness via Eqs.(5) and (6).
In the ABEEMσπ model, the FFs of center atoms were calculated by Eq.(11), then their GFFs were calculated by Eq.(12). Their global softness was obtained by Eq.(11) because of it being the inverse of the hardness, hence the local softness and the GLS were calculated by Eqs.(2) and (13), respectively.
3.3 Exp ression of the local HSAB p rincip le under the finite d ifference app roach and ABEEMσπ m odel
The local HSAB principle claimed19that the interaction between two molecules w ill occur not necessarily through their the softest atoms but rather through those atoms of two systems, and their Fukui functions of which are close. Based on this principle, the softness-matching criteria was proposed by Chandea, Nguyen, Geerlings and coworkers for understanding the regioselectivity of cycloaddition reactions11–13,15,16. The softness-matching criterion at a local-local approach in the case of multiple sites of interaction has been cast in the form of the m inim ization of a quadratic form to articulate. In our investigated reactions, because there are two reaction center atoms in electrophilic additions, we w ill use the absolute values of differences between the local softness of the reaction center atoms of two reactants to express.
Hence, w ithin the FDA method, the expression of the local HSAB principle is w ritten as Eq.(14), where the i is the site of reactivity on molecule A, and the k is the site of reactivity on molecule B, as seen in Fig.1, and theis the condensed local softness of the i th atom in A, which represents that the electrophile H atom in HCl or [PhSe] group in PhSeBr acquires a electron sharing from the π-bond of substituted ethene and theis the condensed local softness of the k th atom in B, which represents that the reactant B w ill be attacked by H atom or[PhSe] group to donate an electron to be shared. And then,based on the proposed generalized reactivity descriptor, the local HSAB principle can be expressed as the Eq.(15). In this kind of the reaction, the superscript + denotes the reactivity descriptor of the electrophilic H atom, while the superscript –represents the reactivity index of double bond C atom in alkene.

According to the local HSAB principle, the smaller the Δs or ΔsGis, the easier the reaction is. In this paper, we only consider the state of single reactant, when ΔsMA< ΔsAMor<Δ, the Markovnikov product should be the main; and when ΔsMA> ΔsAMorA>, the anti-Markovnikov product should be favored. And the generalized reactivity descriptor can be further used to rationalize the reaction rate constants,i.e., the greater theis, the greater the reactivity is, and the easier the reaction is.
Tab le 2 The difference values, Δs MA, Δs AM, Δ and Δ, for HCl w ith alkene in term s of MP2/6-311++G(d,p) level under thefinite difference approximation, and our ABEEMσπ model.

Tab le 2 The difference values, Δs MA, Δs AM, Δ and Δ, for HCl w ith alkene in term s of MP2/6-311++G(d,p) level under thefinite difference approximation, and our ABEEMσπ model.
Finite difference approximation ABEEMσπ model Δs MA Δs AM Δs G AM Δs G MA 103Δs MA 103Δs G AM 10Δs G MA 10Δs G MA ethene 0.589 0.589 2.647 2.647 0.069 0.069 0.526 0.526 propene 0.533 0.581 6.017 5.579 2.099 9.250 0.739 1.760 1-butene 0.549 0.556 8.863 8.779 2.867 5.727 0.981 2.012 2-methylpropene 0.604 0.627 8.195 7.924 3.008 6.643 0.964 2.122

Table 3 The values of condensed f(r), f G(r), s(r), and s G(r) for the H atom of electrophile HCl and the C MA and C AM of unsymmetrical alkenes at the level of MP2/6-311++G(d,p) and the ABEEMσπ model.
4 Resu lts and d iscussion
4.1 Regioselec tivity of the add ition of HCl to alkene
For the addition of HCl to unsymmetrical olefin CH2=CR1R2, when the substituent is electron-donating group, such as alkyl, the reactions comply w ith the Markovnikov’s rules to occur. When the substituent is electron-accepting group, such as ―CHO, ―COOH, the reactions comply w ith the anti-Markovnikov’s rules. As seen in Fig.1, these substituents belong to the alkyls, so the regioselectivities of these reactions abide by the Markovnikov’s rules to produce the Markovnikov’s products.
According to Eqs.(14)–(17), the difference values, Δ sMA,Δ s , Δ sGand Δ sG, for the reactions of HCl w ith CH2=AM MA MA CR1R2were calculated by using the FDA method and the ABEEMσπ model, and listed in Table 2. Table 3 presents the detailed values of FF, GFF, local softness, and GLS of reactive center atoms obtained from these two methods.
As shown in Table 2, follow ing the FDA method, the values of ΔsMA(0.589), ΔsAM(0.589) and(2.647),(2.647)for the reaction between HCl w ith ethene are equal to each other, respectively, which, of course, indicates that there is no regioselectivity in this reaction. When the olefin is propene, the value of ΔsMA(0.533) is smaller than the relevant(0.581).According to the local HSAB principle, the H atom of HCl favors to attack the Markovnikov’s carbon atom, so this result is in line w ith the experimental regioselectivity. However, the value of6.017) is greater than theM (5.579) by using the generalized local softness, then the regioselectivity of this reaction would be anticipated the anti-Markovnikov’s attacking. But, this result is not in agreement w ith the experimental result. By using the same way to deal w ith the rest two additions of HCl to 1-butene and 2-methylpropene, we also obtain Δs MA < Δs AM and>. Hence, according to the local HSAB principle, w ithin the FDA method, the predicted results obtained from the usual local softness are better than those from the generalized local softness (GLS).
And then, how about are the results in terms of the ABEEMσπ model? It is clearly seen from Table 3 that the both values of ΔsMAand ΔsAMare 0.069 × 10−3, and both ΔsGMAandare 5.26 when the olefin is ethene, which indicates that the two double-bonded carbon atoms are identical. When R1is H and R2is ―CH3, Δ sMAis 2.099 × 10−3, Δ sAMis 9.250 ×10−3andis 73.9,is 17.60, i.e., Δ sMA< Δ sAMand<. Therefore, on basis of local HSABA AM principle, the Markovnikov’s product should constitute the main product of this reaction, and this result is in agreement w ith the Markovnikov’s rules. In the same way, when alkenes are 1-butene and 2-methylpropene, both Δ sMA< Δ sAMand<, so the results are consistent w ith the Markovnikov’s rules. Consequently, both Δs via usual local softness and Δ sGvia GLS from ABEEMσπ model can explain and forecast the regioselectivities of these reactions well, and the predicted results are better than those of the FDA method.
It was reported that the rate constants for the addition of HI to ethene, propene, and 2-methylpropene were in the ratio 1:90:7005,6, which indicated that w ith raising the substituents,the reaction rates gradually became greater and greater.Furthermore, experimental activation energies of the additions of HCl to ethene (166.105 kJ·mol−1), to propene (144.348 kJ·mol−1), and to 2-methylpropene (119.244 kJ·mol−1) were reported2,9, which implied when the substituents gradually become larger and larger, the additions of HCl to CH2CR1R2are more and more easy to process. The generalized reactivity descriptors, GFF and GLS themselves, can rationalize the intermolecular reactivity, and especially forecast the order of reaction rate constants for a series of reactions. Hence, we applied the GLS, rather than Δ sGto correlate the order of the reaction rate constants for these investigated additions.
The investigated electrophilic additions of HCl to alkenes,we have only considered the reactivity descriptors of reactants,which means that the values of GLS for the H atom of HCl are fixed and just the values of GLS for the CMAof alkenes are taken as variables, where the values of GLS for reaction centers by FDA method and ABEEMσπ model are listed in Table 3,i.e., we can disregard the GLS of H atom in HCl and only compare the GLS of CMAin alkenes of the main product. It is clear from our calculations that the values ofobtained from both FDA method and ABEEMσπ model (in Table 3) for alkenes increase w ith the substituents rising. Since the higher FF is, the higher reactivity is, i.e., the softest position of the molecule is, the easiest reactive site occurs. Hence, the addition for HCl to 2-methylpropene is the fastest reaction, the addition for HCl to ethene is the slowest one, and the addition of HCl to 1-butene is in the middle. These conclusions are just in agreement w ith experimental results and the results of usual local softness have not such regularity.
In a word, both the usual reactivity descriptors and the generalized ones from ABEEMσπ model in combination w ith the local HSAB principle can successfully interpret and forecast the regioselectivities of the additions of HCl to alkenes, which results are in agreement w ith the Markovnikov rule, but the results of FDA method are not good. And then, the values offor the alkenes calculated by both the FDA method and the ABEEMσπ model can further correlate the reaction rate constants. When values ofgradually become big, the studied additions gradually become fast as substituents gradually increasing. But, the usual softness ofcan not do this result. Therefore, we have chosen the other series of electrophilic additions tofurther check the validity and practicability of generalized descriptors again, as seen in Fig.1.
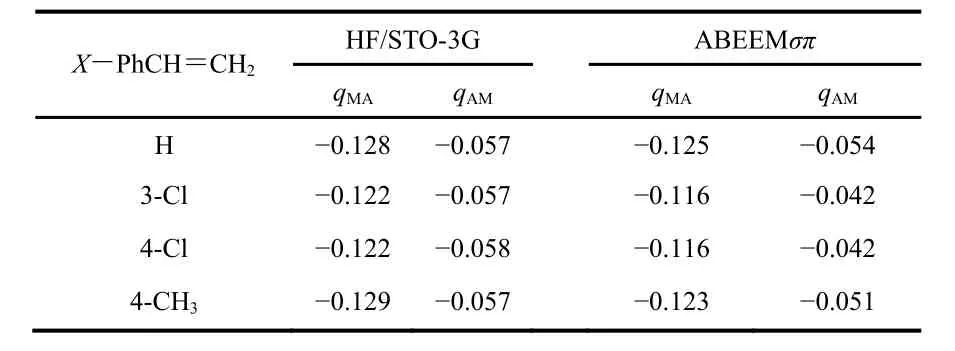
Table 4 The charges of CMA, CAM obtained from HF/STO-3G andABEEMσπ M odel.
4.2 The regioselec tivity of add ition fo r benzeneseleny l b rom ide w ith alkene
The additions of benzeneselenyl bromide to alkenes are usually considered to be the electrophilic addition reactions7.We have chosen four reactions between benzeneselenyl bromide and substituted styrene (X PhCH=CH2), where the substituents Ph X of alkenes are Ph, 3-ClPh, 4-ClPh and 4-CH3Ph, respectively. Here, [PhSe] group in electrophile is considered to be the H atom of HCl and it has the positive charge, which attacks one of the double-bonded carbon atoms of alkenes w ith enriched electron. The Br atomic charges obtained by HF/STO-3G level of theory and ABEEMσπ model are −0.100 and −0.140 a.u., respectively. Table 4 lists the charges of CMAand CAM, qMAand qAM, calculated by HF/STO-3G level of theory and ABEEMσπ model,respectively.
These CMApossess much more negative charge and the CAMpossess a little charge compared w ith CMA, hence, the electrophile [PhSe] group w ill favor to attack the CMA. Here,we could consider the substituents X together w ith benzene(X―Ph―) as a whole to be the electron-donating groups, i.e.these four reactions should obey the Markovnikov’s rules according to the greater attraction between [PhSe] group and CMA, which are just in line w ith the experimental results7. We also can see that the qMAof 3-Cl and 4-Cl are less than that of the others, because the interaction between ―Cl, the electron-w ithdraw ing group, and benzene, the electron-donating group, represents the character of the electron-donating group in nonpolar solution, so leading to that result, if the reactions react in polar solution, the result may be the opposite7, however, the all calculations about these reactions were calculated at the gas state in vacuum. The charges of ABEEMσπ and ab initio method are in agreement by and large.
Then, we make use of the usual local softness and the generalized one from FDA method and the ABEEMσπ model combination w ith local HSAB principle to estimate the regioselectivities of above four additions, the values of ΔsMA,Δ s , Δ sGand Δ sGfrom these two methods are listed in AM MA AM Table 5, and the ratio of Markovnikov’s product to anti-Markovnikov’s from the experiment7are also listed in Table 5.
It can be seen from that Table 5 the fourandare all smaller than respective Δ sAMandunder the FDA method. And the values of Δ sMAandfrom ABEEMσπ model are also smaller than their respective Δ sAMand. Therefore, on basis of local HSAB principle, the Markovnikov’s products should constitute the main products of these four reactions by means of FDA method and ABEEMσπ model, which results are in line w ith the experimental regioselectivities.
Table 5 The values of Δs MA, Δs AM, and for PhSeBr w ith substituted styrene (X-PhCH=CH 2) at the level of MP2/6-311++G(d,p) w ith the finite difference approach and ABEEMσπ model.
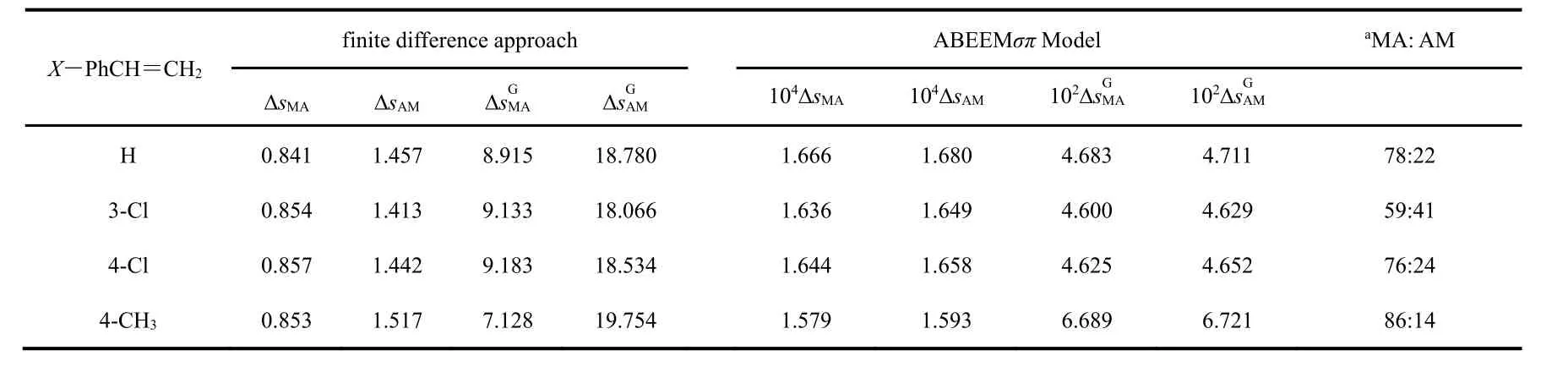
Table 5 The values of Δs MA, Δs AM, and for PhSeBr w ith substituted styrene (X-PhCH=CH 2) at the level of MP2/6-311++G(d,p) w ith the finite difference approach and ABEEMσπ model.
a Those reactions are reacting in benzene at 25 °C.
X―PhCH=CH2finite difference approach ABEEMσπ Model aMA: AM Δs MA Δs AM Δs G MA Δs G AM 104Δs MA 104Δs AM 102Δs G MA 102Δs G AM H 0.841 1.457 8.915 18.780 1.666 1.680 4.683 4.711 78:22 3-Cl 0.854 1.413 9.133 18.066 1.636 1.649 4.600 4.629 59:41 4-Cl 0.857 1.442 9.183 18.534 1.644 1.658 4.625 4.652 76:24 4-CH3 0.853 1.517 7.128 19.754 1.579 1.593 6.689 6.721 86:14

Fig.2 The line charts of the reaction rates (upper), the s G (m idd le) and s G− (lower) of CMA atom s in the four additions of benzeneselenyl brom ide to the substituted styrenes.
We can obtain two sequences:4-CH3)<(H)<(3-Cl)<(4-Cl) via FDA method and(3-Cl)<(4-Cl)<(H)< ΔsG(4-CH)via ABEEMσπMA 3 model. According to the local HSAB principle, the smaller Δ sGis, the easier reaction is. Luk and his coworkers7gave second-order rate constants, k, its unit being dm3·mol−1·s−1of these reactions which are in order kH(2.58 ± 0.15) × 10−2, k3-Cl(1.57 ± 0.07) × 10−2, k4-Cl(2.20 ± 0.1) × 10−2, and k4-CH3(2.77 ±0.1) × 10−2, as shown in Fig.2 (upper). The order of the experimental reaction rates is k3-Cl< k4-Cl< kH< k4-CH3.Therefore, the intermolecular reactivity predicted by ABEEMσπ model is just in a reverse order compared w ith the experimental rate constants.
Fig.2 (middle) displays the line chart of the sGobtained from the ABEEMσπ model. And Fig.2 (lower) represents the line charts of the sG−of the CMAatoms calculated by FDA method.It can be found from the Fig.2 that the order ofis4-Cl) <3-Cl) <H) <(4-CH3) (FDA method) and that ofis(3-Cl) <(4-Cl) <(H) <(4-CH3)(ABEEMσπ model). The sequence via ABEEMσπ model is just in accord w ith that of the experimental reaction rates, but that of FDA method is not for the ―Cl substituted additions.
Therefore, the applications of the generalized reactivity descriptor combined w ith the local HSAB principle on this series of electrophilic additions demonstrate that both the values of Δs and ΔsGfrom ABEEMσπ model can forecast their regioselectivities and only the values of center atoms’generalized local softness of substituted ethenes calculated by ABEEMσπ model can rationalize the reaction rate constants rather than the difference of center atoms’ generalized local softness of the two reactants. However, the results of the finite difference approximation are not well related to the experimental results.
5 Conc lusions
For the addition reactions of HCl to the substituted ethenes and benzeneselenyl brom ide to the substituted styrenes,according to the local HSAB principle, the values of the softness differences,sΔ, in terms of ab initio method at the level of MP2/6-311++G(d,p) w ith the finite difference approximation (FDA) method and the ABEEMσπ model have been used to relate to their regioselectivities.
As the performance of the generalized reactivity descriptor, it is shown that the CMAatoms of all reactions prefer to be attacked in terms of ABEEMσπ model, which is in agreement w ith the experimental results. But, the results of FDA method can not obtain such good indication. However, it is shown that there are two inverse orders, compared w ith the orders of experimental rate constants for these two series of electrophilic additions by using the ΔsGfrom FDA and ABEEMσπ model. In fact, only generalized local softness (GLS) of center atoms can be related to the orders of the experimental reaction rate constants by both the FDA method and the ABEEMσπ model except the results of the FDA method for 3-Cl substituted addition w ith a little flaw.
Up to now, we have applied the generalized reactivity descriptors to study on several kinds of reactions, such as to predict the regio- and stereoselectivity of Diels-Alder reactions and to correlate their reaction rate constants, to rationalize the intermolecular reactivities and regioselectivities of enzymatic catalyzed nucleophilic reactions, etc. Moreover, we w ill continue to apply the generalized Fukui function and the generalized local softness to investigate other systems and tofurther check their rationality and validity.
References
(1) Yang, Z. -Z.; Ding, Y. -L.; Zhao, D. -X. ChemPhysChem 2008, 9,2379. doi: 10.1002/cphc.200800364
(2) Suresh, C. H.; Koga, N.; Gadre, S. R. J. Org. Chem. 2001, 66, 6883.doi: 10.1021/jo010063f
(3) Aizman, A.; Contreras, R.; Galvan, M.; Cedillo, A.; Santos, J. C.;Chamorro, E. J. Phys. Chem. A 2002, 106, 7844.doi: 10.1021/jp020214y
(4) Menendez, M. I.; Suarez, D.; Sorod, J. A.; Sordo, T. L. J. Comput.Chem. 1995, 16, 659. doi: 10.1002/jcc.540160602
(5) Benson, S. W.; Bose, A. N. J. Chem. Phys. 1963, 39, 3463.doi: 10.1063/1.1734215
(6) Bose, A. N.; Benson, S. W. J. Chem. Phys. 1963, 38, 878.doi: 10.1063/1.1733776
(7) Luh, T. -Y.; So, W. -H.; Cheung, K. S.; Tam, S. W. J. Org. Chem. 1985,50, 3051. doi: 10.1021/jo00217a006
(8) Rauk, A. Orbital Interaction Theory of Organic Chemistry, 2nd ed.;John Wiley & Sons, Inc.: New York, USA, 2001.
(9) Sathre, J. L.; Thomas, T. D.; Svensson, S. J. J. Chem. Soc., Perkin Trans 2 1997, 28, 749. doi: 10.1002/chin.199730041
(10) Markovnikov, V. Ann. Chem. Pharm. 1870, 153, 228.doi: 10.1002/jlac.18701530204
(11) Chandra, A. K.; Nguren, M. T. J. Comput. Chem. 1998, 19, 195.doi: 10.1002/(SICI)1096-987X(19980130)19:2<195::AID-JCC12>3.0.CO;2-H
(12) Chandra, A. K.; Nguyen, M. T. J. Phys. Chem. A 1998, 102, 6181.doi: 10.1021/jp980949w
(13) Damoun, S.; Woude, V. D.; Mendez, F.; Geerlings, P. J. Phys. Chem.A 1997, 101, 886. doi: 10.1021/jp9611840
(14) Geerlings, P.; De Proft, F. Int. J. Quantum Chem. 2000, 80, 227. doi:10.1002/1097-461X(2000)80:2<227::AID-QUA17>3.0.CO;2-N
(15) Nguyen, L. T.; De Proft, F.; Dao, V. L.; Nguyen, M. T.; Geerlings, P.J. Phys. Orgs. Chem. 2003, 16, 615. doi: 10.1002/poc.653
(16) Nguyen, L. T.; Le, T. N.; Proft, F. D.; Chandra, A. K.; Langenaeker,W.; Nguyen, M. T.; Geerlings, P. J. Am. Chem. Soc. 1999, 121, 5992.doi: 10.1021/ja983394r
(17) Sengupta, D.; Chandra, A. K.; Nguren, M. T. J. Org. Chem. 1997, 62,6404. doi: 10.1021/jo970353p
(18) Li, Y.; Evans, J. N. S. J. Am. Chem. Soc. 1995, 117, 7756.doi: 10.1021/ja00134a021
(19) Gazquez, J. L.; Mendez, F. J. Phys. Chem. 1994, 98, 4591.doi: 10.1021/j100068a018
(20) Geerlings, P.; Proft, F. D.; Langenaeker, W. Adv. Quantum Chem.1998, 33, 303. doi: 10.1016/S0065-3276(08)60442-6
(21) Xu, Z. -Z.; Zhao, D. -X.; Yang, Z. -Z. Chin. Sci. Bull. 2012, 57, 2787.doi: 10.1360/972012-537
(22) Zhao, D. -X.; Xu, Z. -Z.; Yang, Z. -Z. Int. J. Quantum Chem. 2013,113, 1116. doi: 10.1002/qua.24173
(23) Geerlings, P.; Proft, F. D.; Langenaeker, W. Chem. Rev. 2003, 103,1793. doi: 10.1021/cr990029p
(24) Parr, R. G.; Yang, W. Density Functional Theory of Atom and Molecules; Oxford University Press: New York, USA, 1989.
(25) Parr, R. G.; Yang, W. T. J. Am. Chem. Soc. 1984, 106, 4049.doi: 10.1021/ja00326a036
(26) Yang, Y.; Parr, R. G. Proc. Natl. Acad. Sci. USA 1985, 82, 6723.doi: 10.1073/pnas.82.20.6723
(27) Padmanabhan, J.; Parthasarathi, R.; Elango, M.; Subramanian, V.;Krishnamoorthy, B. S.; Gutierrez-Oliva, S.; Toro-Labb, A.; Roy, D. R.;Chattaraj, P. K. J. Phys. Chem. A 2007, 111, 9130.doi: 10.1021/jp0718909
(28) Baekelandt, B. G.; Janssens, G. O. A.; Toufar, H.; Mortier, W. J.;Schoongeydt, R. A. J. Phys. Chem. 1995, 99, 9784.doi: 10.1021/j100024a020
(29) Baekelandt, B. G.; Mortier, W. J.; Lievens, J. L.; Schoonheydt, R. A.J. Am. Chem. Soc. 1991, 113, 6730. doi: 10.1021/ja00018a003
(30) Baekelandt, B. G.; Mortier, W. J.; Schoonheydt, R. A. The EEM Approach to Chemical Hardness in Molecules and Solids:Fundamentals and Applications, Structruce and Bonding; Springer:Berlin Heidelberg, Germany, 1993; Vol. 80, pp. 187–227.
(31) Bultinck, P.; Langenaeker, W.; Lahorte, P.; De Proft, F.; Geerlings, P.;Waroquier, M.; Tollenaere, J. P. J. Phys. Chem. A 2002, 106, 7887.doi: 10.1021/jp0205463
(32) Bultinck, P.; Langenaeker, W.; Lahorte, P.; Proft, F. D.; Geerlings, P.;Alsenoy, C. V.; Tollenaere, J. P. J. Phys. Chem. A 2002, 106, 7895.doi: 10.1021/jp020547v
(33) Janssens, G. O. A.; Toufar, H.; Baekelandt, B. G.; Mortier, W. J.;Schoonheydt, R. A. Stud. Surf. Sci. Cat. 1997, 105, 725.doi: 10.1016/S0167-2991(97)80622-2
(34) Mortier, W. J.; Ghosh, S. K.; Shankar, S. J. Am. Chem. Soc. 1986, 108,4315. doi: 10.1021/ja00275a013
(35) Cong, Y.; Yang, Z. Z. Chem. Phys. Lett. 2000, 316, 324.doi: 10.1016/S0009-2614(99)01289-0
(36) Yang, Z. -Z.; Wang, J. -J.; Zhao, D. -X. J. Comput. Chem. 2014, 35,1690. doi: 10.1002/jcc.23676
(37) Zhao, D. X.; Liu, C.; Wang, F. F.; Yu, C. Y.; Gong, L. D.; Liu, S. B.;Yang, Z. Z. J. Chem. Theory Comput. 2010, 6, 795.doi: 10.1021/ct9006647
(38) Liu, C.; Li, Y.; Han, B. -Y.; Gong, L. -D.; Lu, L. -N.; Yang, Z. -Z.;Zhao, D. -X. J. Chem. Theory Comput. 2017, 13, 2098.doi: 10.1021/acs.jctc.6b01206
(39) Liu, L. -L.; Yang, Z .-Z.; Zhao, D. -X.; Gong, L. -D.; Liu, C. RSC Adv.2014, 4, 52083. doi: 10.1039/c4ra09631b
(40) Wu, Y.; Yang, Z. Z. J. Phys. Chem. 2004, 108, 7563.doi: 10.1021/jp0493881
(41) Yang, Z. Z.; Cui, B. Q. J. Chem. Theory Comput. 2007, 3, 1561.doi: 10.1021/ct600379n
(42) Yang, Z. Z.; Qian, P. J. Chem. Phys. 2006, 125, 064311.doi: 10.1063/1.2210940
(43) Yang, Z. Z.; Wu, Y.; Zhao, D. X. J. Chem. Phys. 2004, 120, 2541.doi: 10.1063/1.1640345
(44) Yang, Z. Z.; Zhang, Q. J. Comput. Chem. 2006, 27, 1.doi: 10.1002/jcc.20317
(45) Zhang, Q.; Yang, Z. Z. Chem. Phys. Lett. 2005, 403, 242.doi: 10.1016/j.cplett.2005.01.011
(46) Wang, C. S.; Yang, Z. Z. J. Chem. Phys. 1999, 110, 6189.doi: 10.1063/1.478524
(47) Yang, Z. Z.; Wang, C. S. J. Phys. Chem. A 1997, 101, 6315.doi: 10.1021/jp9711048
(48) Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb,M. A.; Cheeseman, J. R.; Montgomery, J. A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J. C.; et al. Gaussian 03, Revision C.02; Gaussian, Inc.:Wallingford, CT, USA, 2004.
(49) Derouane, E. G.; Fripiat, J. G.; Ballmoos, R. V. J. Phys. Chem. 1990,94, 1687. doi: 10.1021/j100367a085
(50) Wilson, M. S.; Ichikawa, S. J. Phys. Chem. 1989, 93, 3087.doi: 10.1021/j100345a041
(51) Torrent-Sucarrat, M.; Proft, F. D.; Geerlings, P.; Ayers, P. W. Chem.Eur. J. 2008, 14, 8652. doi: 10.1002/chem.200800570
(52) Huzinaka, S.; Sakai, Y.; M iyoshi, E.; Narita, S. J. Chem. Phys. 1990,93, 3319. doi: 10.1063/1.458812
(53) Jakalian, A.; Bush, B.; Jack, D. B.; Bayly, C. I. J. Comput. Chem.2000, 21, 132. doi: 10.1002/(SICI)1096-987X(20000130)21:2<132::AID-JCC5>3.0.CO;2-P
- 物理化学学报的其它文章
- RbCl和CsCl水溶液结构的X射线散射及经验势结构精修模拟
- Adso rp tion of Hyd razoic Acid on Pristine Graphyne Sheet:A Com pu tational Study
- Chem ical Bond ing and In terp retation of Tim e-Dependen t Elec tronic Processes w ith Maxim um Probability Dom ains
- 芘二酰亚胺:兼具高电子迁移率和双光子荧光性能的有机半导体
- Generalized Hirsh feld Partitioning w ith Orien ted and Prom o ted Proatom s
- TPE核的螺旋手性

