基于相关器原理的图像特征识别方法
区 彤,宋明明,周惠君,高文莉
(南京大学 物理学院,江苏 南京 210093)
光学图像特征识别的目的是识别检测图像中是否含有参考图像的信息. 传统的光学图像特征识别方法[1-2]通常采用全息法制作与参考图像对应的匹配滤波器,然后将检测图像放置在4f系统中,并把制作好的匹配滤波器置于该系统中检测图像的频谱位置处,识别结果是:如果检测图像含有参考图像信息,则4f系统末端的像屏上会显示清晰的亮点,否则会出现弥散的光斑. 该方法的局限性在于,不能识别出与参考图像形状相同,但相对于参考图像有缩放或旋转的检测图像,对此,可以对检测图像的频谱进行ln-θ坐标变换来消除缩放和旋转的影响[3-5].ln-θ坐标变换在一定程度上降低了光学图像特征识别的难度.
本文在光学图像特征识别中加入计算机处理,通过编写计算机程序实现光学图像特征识别中难度较高的步骤,简化了光学图像特征识别过程,降低了其难度.
1 原理分析
1.1 相关器原理
设参考图像的场强分布为f(x,y),检测图像的场强分布为g(x,y),则函数f(x,y)和g(x,y)的相关函数定义为[1]
(1)
其中f*(x,y)指f(x,y)的复共轭. 如果f(x,y)=g(x,y),可以得到f(x,y)的自相关函数为
(2)

(3)
(4)
显然uff(x,y)在(0,0)处有极大值:
(5)
(6)
等号当且仅当g(x,y)=kf(x,y)时成立(k为常数). 这说明若检测图像和参考图像的光强分布不同,其相关输出总是比参考图像的自相关输出的极大值小,这就是相关器原理[1]. 因此,可以通过比较检测图像和参考图像的相关输出以及参考图像的自相关输出的大小,判断检测图像含有多少参考图像的信息,即检测图像和参考图像的相似程度.
1.2 相关性定理及平移对自相关函数的影响
由相关性定理[1]
F[g(x,y)*f(x,y)]=F[g(x,y)]·
F*[f(x,y)]=G(fX,fY)·F*(fX,fY)
(7)
可知,2个函数的相关函数的傅里叶变换等于1个函数的傅里叶变换和另1个函数的傅里叶变换的复共轭的乘积. 该定理是在计算机上计算相关函数的理论依据.
考虑检测图像的光强分布和参考图像相同,但相对参考图像有平移的情况,即g(x,y)=f(x-x0,y-y0),根据相关性定理可以证明f(x,y)和g(x,y)的相关函数与f(x,y)的自相关函数有相同的极大值,只是极大值出现的位置发生变化[6].
1.3 ln-θ坐标变换
为了消除检测图像相对于参考图像发生缩放或旋转的影响,可以对检测图像和参考图像均进行ln-θ坐标变换,从而将原图像的旋转和缩放转化为新的坐标平面上的平移变换[3-5]. 根据1.2中的结论,平移不会改变自相关函数的极大值,只会改变其出现的位置,从而消除了检测图像旋转和缩放对识别的影响.
ln-θ坐标变换的基本原理是将定义在(x,y)平面上的函数s(x,y),变换成(u,v)平面上的函数t(u,v),其中有:
考虑到在实验中对输入图像直接进行坐标变换难度较大[5],采用先对输入图像的频谱进行坐标变换,再计算两图像频谱的相关函数的方案. 这样做的合理性在于:
1)因为不同图像的频谱总是不同,所以频谱的相关性可以反映原图像的相关性;
2)可以证明[7]当原图像发生平移、旋转和缩放时,频谱也会相应地发生平移、旋转和缩放,ln-θ坐标变换同样适用.
需要注意的是:虽然ln-θ坐标变换可以将原图像的缩放和旋转转化成新的坐标平面上的平移,但是原图像的平移在进行坐标变换后显然不再对应于新坐标平面上的平移,而对应于其他非线性变换. 因此在进行坐标变换之前,首先应保证检测图像和参考图像间没有相对平移. 这体现在用计算机进行分析时,必须先将2幅图像的原点移到同一位置.
2 实验操作
2.1 实验光路
实验光路如图1所示. 实验中采用液晶光阀输出图像,其工作原理是:在计算机上读入参考图像和检测图像后,计算机将屏幕上的光强信息转化为电信号并传输到液晶盒上,在液晶盒两侧建立与读入光强成正比的电场,该电场改变液晶分子的空间取向. 当线偏振光入射到液晶盒上时,出射光的偏振态由液晶分子的取向决定,而液晶分子的取向由读入图像的光强分布决定,因此在液晶光阀后会产生与输入图像相对应的场强分布f(x,y)和g(x,y)[8-9];透镜L用于对输出的光强分布进行傅里叶变换;照相机用于拍摄输入图像位于透镜L后焦面上的频谱图.

图1 实验光路图
根据傅里叶变换的延迟定理和线性原理可以证明[7],周期性图像频谱可以反映原图像频谱的特征. 而液晶光阀对周期性图像更为敏感,因此将参考图像和检测图像经若干次复制平移的操作做成周期性图像,输入液晶光阀.
2.2 对频谱图的计算机程序处理
将实验中获得的参考图像和检测图像的频谱图F(fX,fY)和G(fX,fY)输入计算机中,进行如图2所示的操作:
1)首先对输入图像取阈值,即设定光强的阈值,大于阈值的光强不变,小于阈值的光强置为0,以去除背景光和杂光,让参考图像和检测图像的频谱信息凸显出来.
2)将2幅图像的原点移至同一位置.

图2 计算机程序处理流程图
3)ln-θ坐标变换,将F(fX,fY)和G(fX,fY)分别变换为H(u,v)和I(u,v).
4)为了突出坐标变换后图像的主要特征,增大不同图像坐标变换结果的差异,缩小相同图像坐标变换结果的差异,提高识别的准确度,进行第2次取阈值操作.
5)对H(u,v)和I(u,v)分别进行傅里叶变换得到J(fu,fv)和K*(fu,fv).
6)根据相关性定理,将J(fu,fv)和K*(fu,fv)逐点相乘后进行逆傅里叶变换,可得H(u,v)和I(u,v)的相关函数H(u,v)*I(u,v).
7)相关函数归一化得到相关输出. 由于H(u,v)和I(u,v)的相关输出实际上反映了原始图像f(x,y)和g(x,y)的相关性,因此将其记为ufg. 另一方面,对2幅参考图像的频谱图进行上述操作可得参考图像的自相关输出,记为uff.
8)最后通过比较ufg和uff的大小,判断检测图像和参考图像的相似程度.
3 实验结果
设计了2组实验来检验该图像特征识别方法:第1组是存在相对缩放和旋转的相同图像间的识别,第2组是不同图像间的识别.
3.1 相同图像间的识别
第1组实验将正立字母A作为参考图像、分别用缩小的A(记为检测图像1)和顺时针旋转60°的A(记为检测图像2)作为检测图像. 先由图1光路拍摄各图像频谱图(图3),然后将其读入计算机中依次进行第1次取阈值操作(图4)、ln-θ坐标变换(图5)以及第2次取阈值操作(图6).
分析图7所示的识别结果:参考图像与检测图像1相关输出的极大值为8 000~9 000,参考图像与检测图像2相关输出的极大值为9 000~10 500,均与参考图像自相关输出的极大值(10 500~12 000)接近,说明检测图像1和检测图像2与参考图像的相似程度均较高. 由此可见,本识别方法能够有效地识别出与参考图像形状相同的检测图像,而不受检测图像缩放和旋转的干扰,这表明在计算机上进行的ln-θ坐标变换操作是有效的.

(a)参考图像

(b)检测图像1

(c)检测图像2
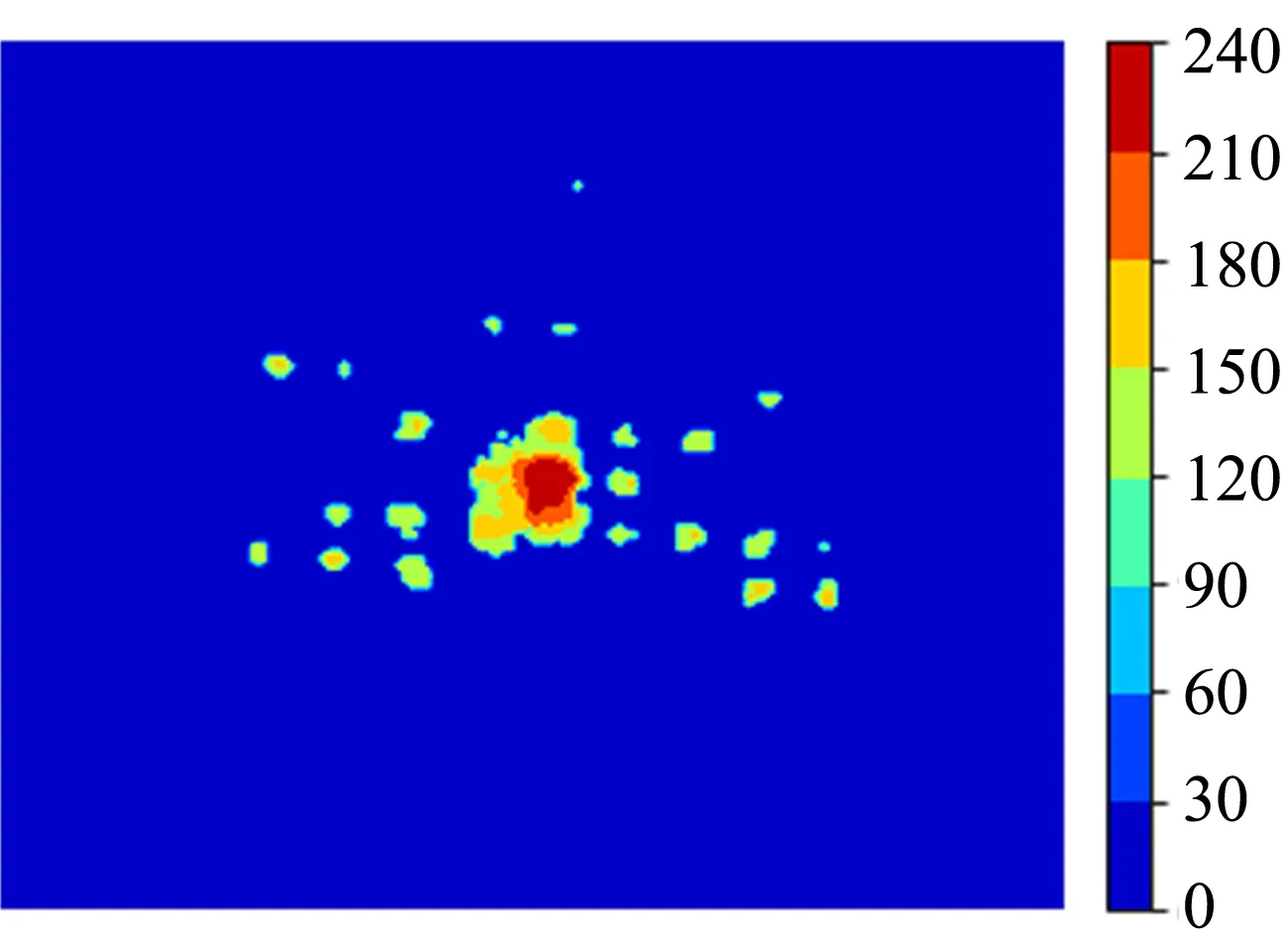
(a)参考图像

(b)检测图像1

(c)检测图像2

(a)参考图像

(b)检测图像1
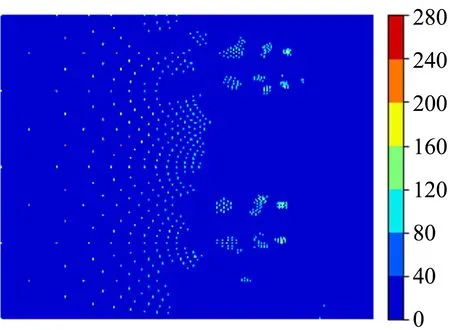
(c)检测图像2

(a)参考图像

(b)检测图像1
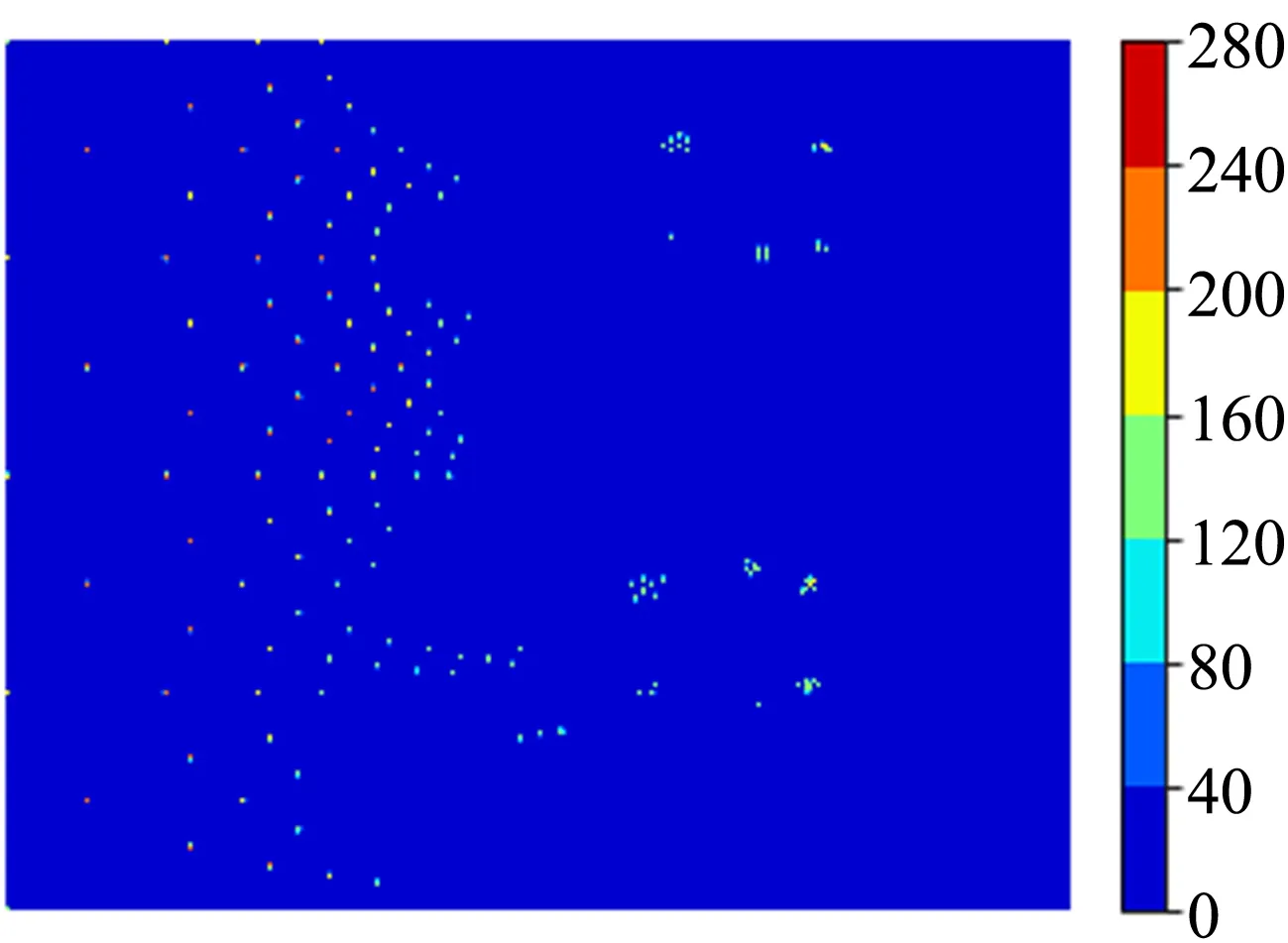
(c)检测图像2
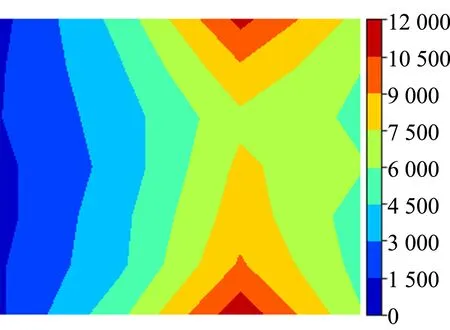
(a)参考图像自相关输出

(b)检测图像1与参考图像的相关输出

(c)检测图像2与参考图像的相关输出
3.2 不同图像间的识别
第2组实验依然将正立字母A作为参考图像,检测图像分别为只含有字母B的图像(记为检测图像3)和既含有A又含有B的图像(记为检测图像4). 先拍摄各图像频谱图(图8),然后将其读入计算机中依次进行第1次取阈值操作(图9)、ln-θ坐标变换(图10)以及第2次取阈值操作(图11).
分析图12所示的识别结果:检测图像3与参考图像相关输出的极大值为6 400~7 200,检测图像4与参考图像相关输出的极大值为6 400~7 200,均远小于参考图像自相关输出(10 500~12 000),说明检测图像3和检测图像4与参考图像的相似程度均不高. 进一步比较图12 (b)和(c)中各点的大小和极大值分布情况可知,检测图像4与参考图像的相似程度比检测图像3高. 由此可见,当检测图像和参考图像不完全相同时,本识别方法能在一定程度上鉴别检测图像含有参考图像信息的多少.

(a)参考图像

(b)检测图像3

(c)检测图像4

(a)参考图像

(b)检测图像3

(c)检测图像4

(a)参考图像
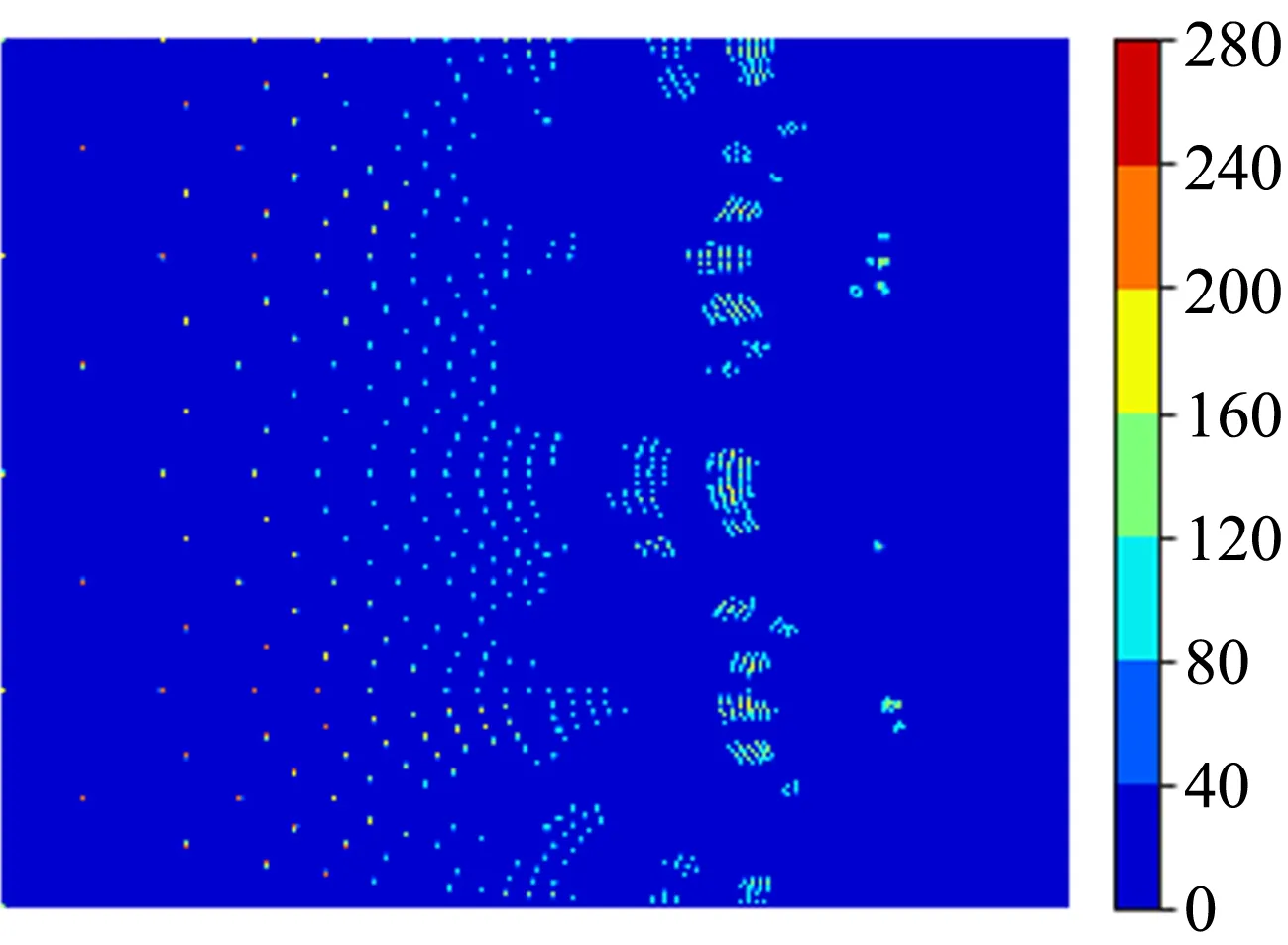
(b)检测图像3

(c)检测图像4

(a)参考图像

(b)检测图像3

(c)检测图像4

(a)参考图像自相关输出

(b)检测图像3与参考图像的相关输出
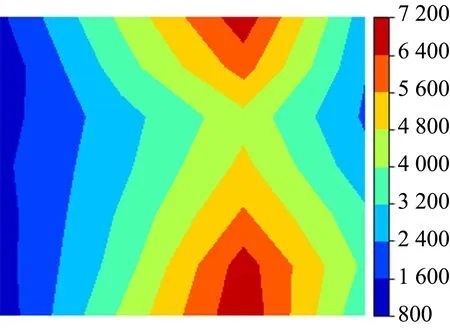
(c)检测图像4与参考图像的相关输出
4 结 论
基于相关器原理,将光学实验和计算机程序处理相结合,提出了图像特征识别方法. 该方法的关键在于计算相关输出和进行ln-θ坐标变换,消除检测图像和参考图像间相对缩放、旋转对识别的影响. 识别的具体操作:先在实验中拍摄检测图像和参考图像的频谱图,后将频谱图读入计算机中进行分析,最后通过比较检测图像和参考图像的相关输出和参考图像的自相关输出的大小来判断检测图像和参考图像的相似程度. 实验结果显示:当检测图像和参考图像形状相同时,该识别方法能消除检测图像和参考图像间相对缩放和旋转的影响,取得很好的识别效果;当检测图像与参考图像不完全相同时,该识别方法能在一定程度上鉴别检测图像含有参考图像信息的多少.
参考文献:
[1] 顾德门J W. 傅里叶光学导论[M]. 詹达三,译. 北京:科学出版社,1976:161-208.
[2] 高文琦. 光学[M]. 3版. 南京:南京大学出版社, 2013:247-252.
[3] Psaltis D, Casasent D. Deformation invariant optical processors using coordinate transformations [J]. Applied Optics, 1977,16(8):2288-2292.
[4] Lee A J, Casasent D, Song J Z, et al. Real-time deformation invariant optical image feature recognition using coordinate transformations [J]. Applied Optics, 1987,26(5):938-942.
[5] Uno K, Kamikozawa Y, Shimizu I. Rotation- and size-invariant object identification system using the liquid crystal on silicon device [J]. Optical Review, 2014,21(3):404-409.
[6] 钟黔川. 光学匹配滤波器在图像特征识别上的研究[D]. 成都:电子科技大学,2001.
[7] 梁昆淼. 数学物理方法[M]. 4版. 北京:高等教育出版社,2010:79-81.
[8] 蔡星汉,缪腾飞,周进. 字母屏的夫琅禾费衍射分析及计算机模拟[J]. 物理实验,2008,28(12):38-42.
[9] 陈波,程翔,谢千里,等. 介绍一个现代化的普物实验——液晶光阀[J]. 大学物理,1999,18(12):31-33.

