数控机床布局设计方案的灰色模糊综合评价

魏金泉,李纬天

(内蒙古工业大学 机械学院，内蒙古 呼和浩特 010051)

0 引言

数控机床布局设计是概念设计中重要的步骤，数控机床布局设计的好坏直接影响概念设计的质量。面对众多数控机床布局设计方案，如何通过评价快速找出其中最优的方案成为每一个数控机床布局设计团队亟待解决的问题。

国内外对数控机床布局进行评价往往使用经验确定、设计公式手册、样本类比等传统评价方法，这些方法含有太多的主观性，导致评价结果不够准确。通过查阅相关文献，灰色关联分析和灰色模糊评价是目前常用的评价方法，但它们在面对复杂的决策评价问题都有各自的局限性，单独使用一种方法进行决策评价时得出的评价结果会有所偏差。针对这一问题，本文使用层次分析法确定指标权重，结合灰色关联分析与灰色综合评价构建灰色模糊综合评价，并以立式数控机床布局设计方案为例进行评价。

1 评价指标体系的建立

在对数控机床布局设计时，需要考虑使用属性、技术经济属性、社会属性三个方面，这也是数控机床布局方案评价的主要内容。数控机床布局方案评价指标体系分2个层次，如图1所示。其中，第一层指标集U={U1,U2,U3},第2层指标集U1={A1,A2,A3},U2={B1,B2,B3,B4,B5,B6},U3={C1,C2}。

2 灰色模糊评价模型构建

模糊综合评价法的优点是数学模型简单，容易掌握，对多因素、多层次的复杂问题评判效果比较好；灰色关联分析法的优点是对样本没有过多的要求，不需要典型的分布规律，计算量小，具有很强的可靠性。本文提出的灰色模糊评价模型就是基于以上两种方法的优点，并结合层次分析法构建的综合评价模型。下面以使用指标U1为例进行灰色模糊评价模型构建。

2.1 评价指标的权重

运用层次分析法来计算指标的权重，其有4种计算权重的方法[1]：几何平均法(方根法)、算术平均法(求和法)、特征向量法和最小二乘法。本文运用算术平均法计算权重。

2.1.1 构造评价指标的判断矩阵

在数控机床布局中，各指标所占的比重是不相同的，使用数字1～9及其倒数定义[2]得到数控机床布局各指标的判断矩阵。判断矩阵标度定义如表1所示。

表1 判断矩阵标度定义

根据表1可得到第二层指标U1={A1,A2,A3}的判断矩阵P1:

(1)

其中：aij为指标U1={A1,A2,A3}中因素两两对比数值。

2.1.2 算术平均法计算权重

由于判断矩阵中的每一行都近似地反映了权值的分配情形，因此可采用全部行向量的算术平均值来估计权向量。以计算指标U1={A1,A2,A3}的权重为例，具体计算步骤如下：

第一步：P1中的元素按列归一化处理。

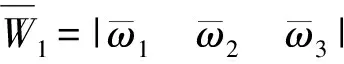
2.1.3 一致性检验

通过一致性检验评价指标的权重分配是否合理。具体过程如下：

(1) 计算一致性指标CI：

(2)

其中：λmax为判断矩阵的最大特征值；y为判断矩阵P1的阶数。

(2) 根据表2查得平均随机一致性指标RI的值。

表2 平均随机一致性指标RI的值

(3) 计算一致性比例CR：

(3)

若CR的值小于0.1，则说明权重分配合理，具有满意的一致性；否则需要对判断矩阵进行适当的修正。

2.2 基于灰色模糊的布局设计方案评价

2.2.1 建立评价方案矩阵

假若有n个方案，专家根据数控机床布局设计方案评价指标体系对各指标进行打分，得到U1={A1,A2,A3}的评价矩阵S1：

(4)

其中：au(X)为评价指标U1={A1,A2,A3}的第X(X=1,2,…,n)个方案第u(u=1,2,3)项评价指标的原始数据。

2.2.2 参数规范化处理

规范化处理评价序列涉及到两个方面:一是对定量指标的规范化处理；二是对定性指标的规范化处理。

定性指标评价常用的语言标度为：好、较好、一般、较差、差，其用模糊数表示，如表3所示。

表3 语言标度的模糊数表示

在对评价指标规范化处理后，可得到规范化处理后的评价指标矩阵：

(5)

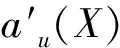
2.2.3 确定参考数据向量

作为参考数据，U1={A1,A2,A3}的参考指标值应为各方案的最优值，因此参考向量的从优隶属度均为1[3]，即：

au(O)={a1(O),a2(O),a3(O)}={1,1,1}.

(6)

2.2.4 计算灰色关联系数

根据灰色理论，灰色关联系数的计算公式[4]为：

(7)

其中：ρ为分辨系数，一般取ρ=0.5。

将规范后的评价矩阵和式(6)的参考向量代入式(7)中可得评价方案灰色关联系数矩阵：

(8)

2.3 评价方案的一级综合评价

将求得的评价指标权重集W1和评价方案灰色关联系数矩阵ξ1相乘可得到一级综合评价模型：

R1=W1ξ1.

(9)

其中：R1为各方案中指标U1={A1,A2,A3}的综合评价值。

同理可以求出指标U2={B1,B2,B3,B4,B5,B6}的综合评价值R2与U3={C1,C2}的综合评价值R3。

2.4 评价方案的二级综合评价

完成一级综合评价之后，得到了第一层指标U1,U2,U3对各方案的综合评价值R1，R2，R3。于是进行二级综合评价。二级决策指标矩阵为：

S=(R1R2R3).

(10)

重复式(5)～式(8)的计算，可得到二级灰色关联系数矩阵ξ，则二级综合评价模型为：

R=Wξ.

(11)

R就是数控机床布局设计中各方案的综合评价值，该值越大说明数控机床布局设计越合理。

综上所述，数控机床布局设计方案的灰色模糊综合评价流程如图2所示。

图2 数控机床布局设计方案灰色模糊综合评价流程

3 方法应用

为了验证评价模型的有效性，以某型号立式数控机床的8种布局方案为例，从使用指标、技术经济指标、社会指标3个主要指标进行评价。数控机床布局方案设计参数如表4所示。依据数控机床的特点与评价体系对数控机床布局设计方案进行评价，评价结果如表5所示。

3.1 评价指标权重计算

邀请数控机床布局设计领域专家，根据数控机床特性对评价指标进行打分以此衡量指标的重要程度。

3.1.1 构造评价指标的判断矩阵

根据专家对U1的打分，由式(1)得到判断矩阵P1：

3.1.2 权重计算

第一步：将P1中的元素按列归一化得：

表4 数控机床布局方案设计参数

表5 数控机床布局设计方案评价值

3.1.3 一致性检验

根据判断矩阵P1可得λmax=3.009 2 ，由式(2)计算一致性指标CI=0.004 6，由表2得RI=0.058，则CR=0.079 3<0.1，即具有较好的一致性。

3.2 基于灰色模糊的布局设计方案评价

3.2.1 建立评价方案矩阵

由表5及公式(4)可得评价矩阵S1：

3.2.2 参数规范化处理

根据表3给出的语言标度的模糊数表示，将评价矩阵S1参数化处理得：

由式(6)和式(7)计算得到灰色关联系数矩阵：

3.2.3 评价方案的一级综合评价

计算得到了使用指标U1、技术经济指标U2和社会指标U3的一级综合评价值：

R1=W1ξ1=[0.428 6 0.600 0 0.428 6 0.479 6 0.479 6 0.584 7 0.940 6 0.940 6].

R2=W2ξ2=[0.711 4 0.616 9 0.734 0 0.756 7 0.555 4 0.553 3 0.6198 0.619 8].

R3=W3ξ3=[1.000 0 0.833 4 0.833 4 0.666 7 1.000 0 0.400 0 0.366 7 0.333 3].

3.2.4 评价方案的二级综合评价

由U1、U2、U3三个指标的评价矩阵得到二级决策指标矩阵：

计算得到权重W和二级灰色关联系数矩阵ξ，则二级综合评价模型为：

R=Wξ=[0.674 8 0.643 6 0.672 2 0.681 1 0.616 7 0.598 6 0.705 6 0.704 1].

3.2.5 评价结果分析

二级综合评价结果就是立式数控机床布局设计方案的评价值。由二级综合评价结果可知：r7>r8>r4>r1>r3>r2>r5>r6。在8种布局设计方案中，方案7优于其他方案。结果基本符合实际情况，因此本文所研究的评价模型是可靠的、科学的，可以运用在机床布局方案设计过程中。

4 结束语

本文充分考虑了影响数控机床布局的因素，并建立数控机床布局方案评价指标体系。运用灰色关联分析法与模糊综合评价法构建了数控机床布局方案的灰色模糊综合评价模型，该模型综合两种评价方法的各自优点，能够避免单一方法在进行评价时容易出现偏差的问题。通过已经成熟的层次分析法计算权重值，可以使评价结果更加科学、可靠。通过实例验证，本文所研究的方法能够有效的对数控机床布局方案进行评价。

参考文献：

[1] 邓雪,李家铭,曾浩健，等.层次分析法权重计算方法分析及其应用研究[J].数学的实践与认识,2012,42(7):93-100.

[2] 常建娥,蒋太立.层次分析法确定权重的研究[J].武汉理工大学学报(信息与管理工程版),2007,29(1):153-156.

[3] 楼锡银,Lou Xiyin.基于灰色关联的机械总体设计方案模糊优选[J].农业工程学报，2010，26(6)：135-140.

[4] 沈健,申浩宇,张海岩，等.直角坐标机器人设计方案的灰色模糊综合评价[J].合肥工业大学学报(自然科学版),2012,35(2):161-164.