基于超-黏弹性的牙周膜本构模型构建及模拟

仵健磊 彭 伟# 董辉跃 姜献峰 刘云峰*

1(浙江工业大学特种装备制造与先进加工技术教育部/浙江省重点实验室，杭州 310014)2(浙江大学浙江省先进制造技术重点实验室，杭州 310027)

引言

牙周膜是连接在牙齿与牙槽骨之间的一层结缔纤维组织，具有支持牙齿，传递、吸收和缓冲咬合力的作用[1-2]。临床正畸治疗中，对于错位牙齿的矫正，牙周膜起着至关重要的作用。一般来说，由矫治器产生的矫治力首先传递给牙齿，再经牙周膜缓冲之后作用在牙槽骨上，从而引起牙槽骨改建等一系列生物反应，并最终在矫治力的作用下，牙齿产生相应的移动和转动，达到正畸的目的。在此矫治过程中，牙周膜起着重要作用，越来越多的学者认为牙槽骨的改建与牙周膜的应力和应变息息相关[3-4]。因此，需要针对牙周膜开展更加深入的研究。

牙周膜作为人体生物组织，实验材料来源有限，只能从捐献尸体的口腔中获取；另一方面，牙周膜为活性组织且极易遭到破坏，正常人体牙周膜厚度为0.2～0.3 mm[5]；牙周膜与其他人体口腔组织分离之后将失去生物活性，所以牙周膜的保存条件也极为苛刻。在实验条件有限的情况下，更多的研究人员采用有限元的方法对牙周膜进行相关研究。目前，有限元法已经在口腔正畸乃至整个医疗领域得到了广泛应用，具有准确度高、重复性好、可操作性强等特点，越来越受到正畸领域人员的青睐[6-9]。

为了更好地研究矫治力-牙周膜应力应变-牙槽骨改建-牙齿移动之间的复杂作用关系，需要建立合适的牙周膜本构模型。在之前的许多有限元工作中，牙周膜多采用线弹性材料模型[10-11]，这显然与实际不符。研究表明，牙周膜的本构关系曲线表现出很强的指数形式[12]。为此，黄辉祥等构建了牙周膜的超弹性模型[1-2]，董晶等将牙周膜设定为双线性模型进行有限元分析[13]，魏志刚等分别将牙周膜设定为线弹性、超弹性及次弹性模型进行研究[14]。但是，相比于弹性材料，牙周膜更贴近黏弹性材料，其黏性作用不能忽视[15]。魏志刚等同时又构建了牙周膜的黏弹性模型，但并没有对黏弹性模型的有效性进行合理的验证[16]；国外学者NataliA等和Iman Z等分别构建了牙周膜的黏弹性模型，但是其模型数据来源为猪和牛，并没有对人体牙周膜进行直接研究，其本构模型参数并不适用于人体牙周膜[4,17]。

为了构建一种准确度高、实用性强的牙周膜本构模型，以人体牙周膜平面剪切和应力松弛实验数据为基础，利用有限元ABAQUS中自带的非线性材料模型，通过实验数据拟合确定符合牙周膜特性的超-黏弹性本构模型及参数，并通过对牙周膜平面剪切实验过程的模拟来验证牙周膜本构模型的正确性，最后通过对比牙周膜线弹性与超-黏弹性模型，分析不同牙周膜本构模型力学响应的差异，为口腔正畸生物力学研究提供有力的理论支持。

1 材料和方法

1.1 人体牙周膜实验数据

为了构建更加准确的牙周膜本构模型，首先需要可靠性好的牙周膜实验数据。牙周膜作为人体生物活性组织，其实验材料的获取受到很大程度的限制，经过查阅大量文献发现，Toms等的牙周膜实验数据具有较高的可信度，这里将以此实验数据为基础进行牙周膜模型的构建[18]。

Toms等的实验牙周膜对象取自一位男性(年龄78岁)尸体的下颌前磨牙，针对前磨牙牙根进行0.85 mm厚度的组织切片处理，最终获得了A1～A5共5组实验试样。牙根组织切片试样包括牙根、牙周膜以及牙槽骨，试样的横断面垂直于牙长轴方向，如图1所示。

针对牙根组织切片试样，分别进行了剪切实验和应力松弛实验，实验测试简图如图 2所示，实验过程中牙槽骨固定，对切片的中间牙根施加位移载荷，压头下压速度为0.2 mm/min。实验中以牙周膜的应变角γ作为应变，以压头受到的反作用力F与牙周膜圆周面积As的比值作为应力，试样厚度为d，牙周膜的宽度为WL，压头的位移量为Δl。

经过对5组牙根组织切片的实验测试，获得了牙周膜剪切实验应力应变曲线和应力松弛曲线，Toms等通过对实验曲线的处理进一步获得了牙周膜剪切应力应变曲线方程和归一化应力松弛曲线方程，如表1所示。接下来，将以该实验数据作为牙周膜本构模型及参数构建的数据基础。

图2 实验测试简图

表1 5组牙周膜试样的剪切应力-应变曲线方程和归一化应力松弛曲线方程

1.2 牙周膜本构模型

牙周膜既不属于符合胡克定律的弹性体，也不属于非牛顿流体，而是介于两者之间的一种高黏弹性体，其力学模型及参数与弹性体和流体均不相同。黏弹性材料的流动变形包括两个阶段：在初始阶段首先表现为一个瞬间的弹性变形，随后是持续一段时间的黏性变形，在此期间保持应变不变的情况下，应力会随着时间而逐步衰减。牙周膜作为一种黏弹性材料，在受载荷的一瞬间表现为超弹性，随后又表现为黏弹性，因此需要分别定义牙周膜的超弹性力学行为和黏弹性力学行为，即超-黏弹性行为[1]，其中超弹性模型的模量时间尺度为瞬态。

1.2.1超弹性本构模型

基于连续介质力学理论，多项式形式模型是最早提出的一种经典本构模型。对于各向同性材料，应变能密度可以分解为应变偏量能和体积应变能两部分，形式如下：

(1)

式中，f和g分别表示应变偏量能和体积应变能。

将式(1)进行泰勒展开，可得

(2)

(3)

一般来说，缩减多项式模型的阶数N越高，其适用性越广。在有限元软件ABAQUS中缩减多项式模型的最高阶数为六阶。这里，将采用缩减多项式模型描述牙周膜的超弹性行为。

1.2.2黏弹性本构模型

(4)

如果将多个Maxwell模型并联或多个Kelvin模型串联起来，就得到了广义Maxwell模型和广义Kelvin模型，后者又称为Kelvin链。对于Kelvin链而言，其本构模型为

(5)

即

(6)

式(5)、(6)即为线性黏弹性本构方程的一般表达。对于不可压缩各向同性材料，体积应力只改变体积，应力偏量导致等体积的形状畸变，而且两种情形下的黏弹特性与效应可分别考虑。因而其本构关系可以表示为

P′·Sij=Q′·eij，P″·σkk=Q″·εkk

(7)

对于大变形黏弹性，又可将其黏弹性本构模型改写成应变能形式，其Prony形式为

(8)

式中，W0为瞬时应变能函数，W∞为稳态应变能函数，δn为能量函数乘子，λn为松弛时间常数，N为阶数，t为时间。

由式(8)，可得名义应力为

(9)

式中，xI为变形状态时的坐标，XJ为初始状态时的坐标。

假设W∞=0，则

(10)

由此可得牙周膜黏弹性的归一化应力松弛函数为

(11)

式(11)为目前有限元软件ABAQUS中用来描述材料黏弹性特性的表达式。

1.3 牙周膜模型数据拟合

为了确定牙周膜本构模型的具体形式以及模型参数，需要基于ABAQUS中现有缩减多项式模型和归一化应力松弛函数模型进行人体牙周膜实验数据拟合，其中牙周膜平面剪切实验的拟合范围是0～0.6 rad，应力松弛实验的拟合范围是0～60 s，分别针对试样A1～A5进行配准拟合，选择拟合度最高的材料模型作为牙周膜的本构模型。

1.4 牙周膜剪切实验的有限元模拟

为验证数据拟合获得的牙周膜本构模型及参数，将针对牙周膜平面剪切实验过程进行有限元模拟，通过对比模拟曲线与实验曲线验证模型的正确性。为简化分析，假设牙根组织切片试样近似为轴对称圆盘结构，取其圆周向截面作为研究对象，并以此建立二维平面轴对称有限元模型，如图3所示(牙槽骨模型未画出)。牙周膜的外侧设置为固定约束，牙周膜的最大应变角为0.6 rad，属性定义采用本文第1.3节拟合获得的牙周膜模型及参数；牙根设定为弹性体，弹性模量为20 000 MPa，泊松比0.3[10]，其上端面以0.2 mm/min的速度施加位移载荷，牙根与牙周膜之间设定为黏结约束。因模型为轴对称模型，同时为了保证计算精度，牙齿和牙周膜单元类型均采用四边形杂交轴对称单元CAX8H。试样A1～A5的建模数据如表2所示，网格单元总数分别为900，1 100，1 100，1 100和1 100。有限元仿真中，以牙周膜的应变角γ作为剪切应变，剪切应力则采用牙根上端面反作用力RF之和与牙根切片厚度d的比值。

图3 实验模拟的有限元模型

1.5 不同牙周膜模型力学响应的对比

为探究牙周膜超-黏弹性模型在正畸治应用的力学响应，以牙周膜线弹性模型为对比，对不同牙周膜模型对正畸力的传递、缓冲效果进行有限元分析。为方便有限元分析计算，简化牙齿、牙周膜为二维平面模型(牙槽骨省略)，如图4所示。牙周膜

表2 实验模拟中试样A1～A5的有限元参数

与牙齿为黏结约束，牙周膜的一侧固定约束，牙根的一侧施加位移载荷，总位移量为0.1 mm，加载时长1 s，为获得较高的计算精度，牙齿与牙周膜网格单元均采用八结点双向二次平面应力四边形单元CPS8R，其中牙根网格单元数为400，牙周膜网格单元数为120。牙周膜厚度取0.25 mm，牙周膜线弹性模型的弹性模量取0.68 MPa，泊松比取0.49[18]；牙周膜超-黏弹性模型取自上述研究结果，材料参数参照A1组试样。

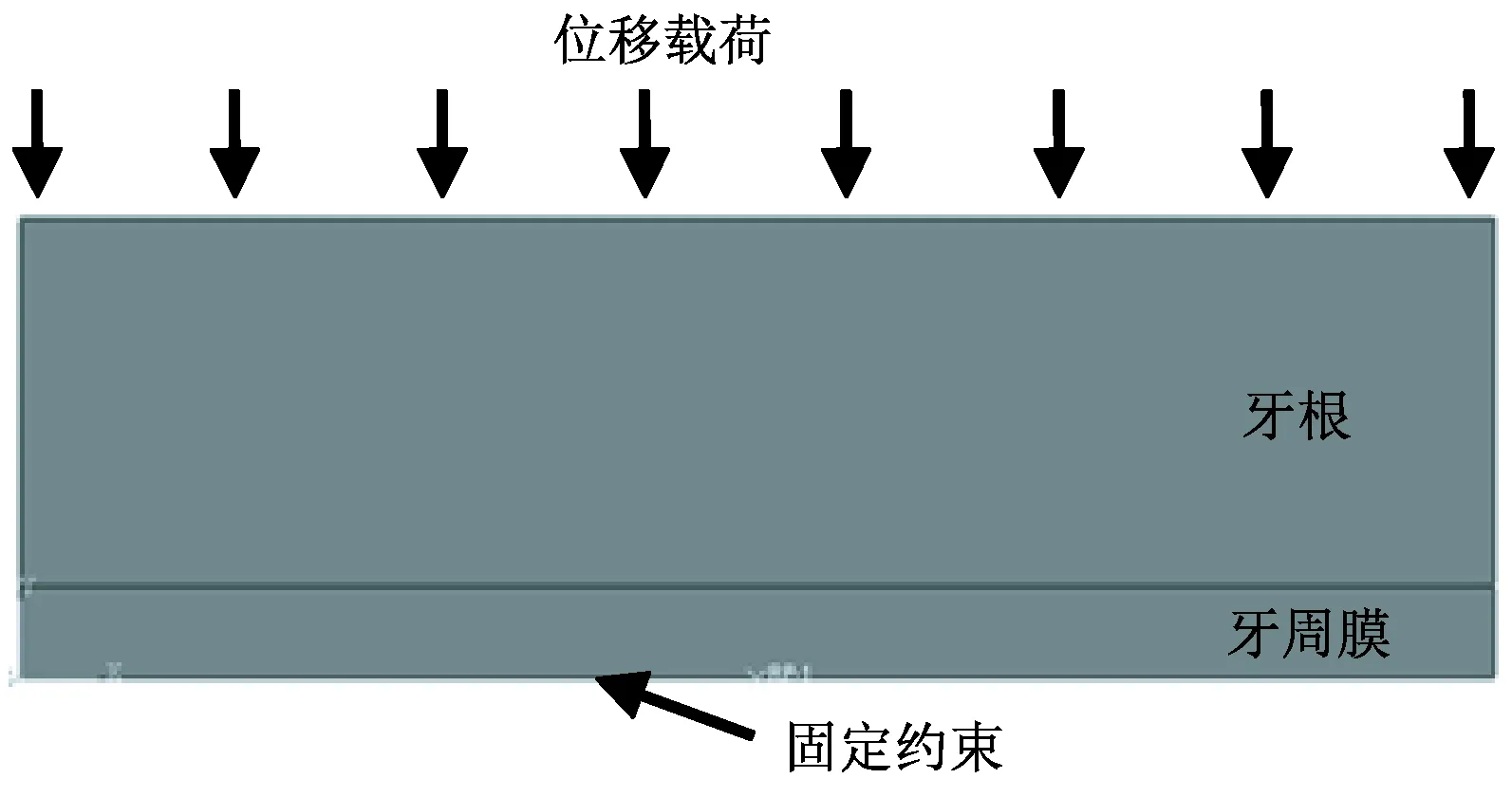
图4 用于牙周膜力学响应对比的有限元模型

2 结果

2.1 牙周膜实验数据拟合及模型参数

以人体牙周膜平面剪切数据为基础，选择缩减多项式模型对牙周膜超弹性特性进行数据拟合，其中试样A1不同阶数缩减多项式模型的拟合结果如图5所示；以牙周膜平面剪切数据和应力松弛实验数据为基础，以归一化的应力松弛函数对牙周膜的黏弹性特性进行拟合，试样A1的黏弹性模型拟合结果如图6所示(其他试样A2～A5拟合曲线与A1基本相同，不再列出)。

从牙周膜超弹性模型的拟合结果来看，缩减多项式的阶数越高，拟合曲线越是贴近于实验曲线，其中六阶缩减多项式数据拟合获得的模型参数列于表3；牙周膜黏弹性模型的拟合曲线与实验曲线完全吻合，拟合获得的参数如表3所示。

图5 超弹性模型拟合曲线

图6 黏弹性模型拟合曲线

2.2 牙周膜剪切实验模拟结果

通过不同牙周膜试样(包括试样A1～A5)平面剪切实验过程的有限元模拟，经后处理获得了牙周膜剪切实验的应力应变曲线，如图7所示。其中，实验曲线是指Toms等在牙周膜平面剪切实验中获得的剪切应力应变曲线，模拟曲线是指利用本文第2.1节中构建的牙周膜本构模型及参数，通过有限元对Toms等的实验过程进行模拟，获得的牙周膜剪切应力应变曲线。

2.3 不同牙周膜模型的力学响应

在相同位移载荷作用下，牙周膜线弹性模型与超-黏弹性模型所产生的力学响应云图(mises应力)如图8所示；利用后处理手段提取牙周膜底侧

表3 牙周膜本构模型曲线拟合参数

图7 5组试样实验曲线与模拟曲线对比结果。(a)试样A1；(b)试样A2；(c)试样A3；(d)试样A4；(e)试样A5

图8 不同牙周膜模型的有限元模拟结果。(a)线弹性模型；(b)超-黏弹性模型

的反作用力，绘制牙周膜反作用力-牙根位移曲线如图9所示。

图9 不同牙周膜模型的力学响应

4 讨论

从牙周膜试样A1平面剪切和应力松弛实验数据的拟合结果图5可以看出，对于缩减多项式模型，模型的阶数越高，拟合曲线越是贴近于实验曲线。在拟合的初始阶段，牙周膜应变角较小，基本所有阶数的缩减多项式模型均能很好地吻合实验曲线，但是当应变角持续增大到0.3 rad时，一阶和二阶缩减多项式模型的拟合效果不够理想，随着应变角的持续增加，一阶和二阶模型不再适用于牙周膜剪切实验的数据拟合。可以看出，低阶缩减多项式模型适用于应变角较小时的数据拟合，而当应变角较大时拟合精度较差。相比低阶缩减多项式模型，高阶模型与实验曲线具有更高的吻合度，当应变角增大到0.6 rad时，四阶、五阶和六阶缩减多项式模型仍能够保持与实验曲线的吻合。但是，在正畸有限元研究工作中，牙周膜的最大应变角不可能只有0.6 rad，选择更高阶数的缩减多项式模型更加有利于准确描述牙周膜的力学行为，为此选择六阶缩减多项式模型描述牙周膜的超弹性特性。

对于牙周膜应力松弛实验的数据拟合，从结果图6来看，归一化的应力松弛函数能够与松弛实验曲线吻合，从而准确描述牙周膜的黏弹性力学行为。从应力松弛的实验曲线以及模拟曲线可以看出，在整个应力松弛过程中，当应变保持不变时，牙周膜的应力是随着时间逐渐减小的。在初始阶段，应力下降的速度较快，随着时间推移，应力的下降趋势逐渐平缓，并逐步趋向于一个稳定值，这完全符合牙周膜的黏弹性特性[18]。

为了验证牙周膜本构模型的准确性，针对牙周膜平面剪切的实验过程进行了有限元模拟，从结果图7来看，5组试样的模拟结果与实验结果基本一致，从而验证了本研究所构建的牙周膜是否黏弹性本构模型的正确性。另外，从模拟结果可以看出， A1、A2、A3、A5试样具有更高的吻合度，A4组试样的拟合度效果不够理想，但模拟结果和实验结果均在同一个数量级，且整体趋势一致。实验曲线与拟合曲线之间存在误差的原因可能是

1)真实的牙根组织切片有一定的锥度，而在有限元建模时将其简化为轴对称的圆盘结构，这种简化可能会对分析结果产生不同程度的影响。

2)实验数据取自一位78岁的男性捐献者，其牙周组织状况相比于年轻人较差，牙周膜的韧性和抗剪切能力较弱。对于A4组试样，其牙周膜厚度为(0.14±0.03)mm，而正常人体牙周膜的组织厚度在0.2～0.3 mm附近[1, 5]，由于其牙周膜薄弱，易受环境因素的干扰，导致实验结果与模拟结果偏差相对较大。

3)为简化有限元分析，假设牙根组织切片近似为圆盘结构，为此只构建了实验试样的二维模型，实际上牙根切片更近似于椭圆柱形，构建牙根切片的三维椭圆模型可能更加贴近于实际情况。

以上情况都可能对模拟结果产生一定的影响，但总体来说，构建的牙周膜超一黏弹性本构模型仍具有较高的准确性。

如图9所示，针对不同牙周膜本构模型对载荷力学响应的模拟结果可知，线弹性模型与超-黏弹性模型存在明显的差异性，线弹性模型的力学响应近似为线性曲线，超-黏弹性模型的响应曲线近似为指数形式。在位移量为0～0.06 mm时，两种模型的力学响应差异较小，超-黏弹性模型曲线略低于线弹性模型曲线，但在位移量超过0.06 mm时，超-黏弹性曲线上升趋势明显，线弹性曲线基本保持原来的曲线斜率上升，两种模型差异越来越大；当位移量为0.1 mm时，线弹性模型的牙周膜作用力大小为2.98 N，超-黏弹性模型的为29.92 N，数量级差异达到10倍。由此可知，在牙周膜变形量较小、计算结果要求不精确时，采用线弹性模型可近似替代牙周膜超-黏弹性模型；但在牙周膜变形量稍大时，线弹性模型力学响应与超-黏弹性模型差异较大，需要构建更符合牙周膜特性的超-黏弹性模型[16]。符合牙周膜材料属性的超-黏弹性本构模型，对于临床正畸的有限元研究则更为准确可靠。

此外，牙周膜作为人体生物组织，其材料来源较少，另一方面牙周膜组织极其薄弱，易受外界因素干扰，这导致人体牙周膜的实验数据较为匮乏。由于只依靠牙周膜的平面剪切数据和应力松弛数据进行牙周膜本构模型的重建，而缺少牙周膜单/双向拉压和体积实验数据，更多类型实验数据的结合更加有利于构建准确度高的牙周膜本构模型[2]，因此对人体牙周膜的实验以及仿真研究仍有许多工作要做。

5 结论

1)由六阶缩减多项式模型和归一化应力松弛函数模型组合成的牙周膜超-黏弹性模型，能够准确拟合牙周膜的平面剪切和应力松弛实验数据。

2)通过对牙周膜平面剪切实验过程的有限元模拟，可以看出所构建的牙周膜本构模型具有很高的准确性。

3)从不同牙周膜本构模型的力学响应，可以看出牙周膜应变较小时可假设为线弹性材料，但应变较大时必须采用更加符合其特性的超-黏弹性模型。

[1] 黄辉祥，汤文成，吴斌，等. 基于超弹性模型的牙周膜生物力学响应 [J]. 东南大学学报(自然科学版)2013, 43(2): 340-344.

[2] 黄辉祥，汤文成，吴斌，等. 基于超弹性模型的牙周膜力学行为数值模拟 [J]. 上海交通大学学报, 2014, 48(9): 1263-1273.

[3] Kawarizadeh A, Bourauel C, Jager A. Experimental and numerical determination of initial tooth mobility and material properties of the periodontal ligament in rat molar specimens [J]. European Journal of Orthodontics, 2003, 25(6): 569-578.

[4] Natali AN, Pavan PG, Carniel EL, et al. Viscoelastic response of the periodontal ligament: an experimental-numerical analysis [J]. Connective Tissue Research, 2004, 45(4-5): 222-230.

[5] 王洪宁，秦行林，刘东旭，等. 基于micro-CT成像的仿真牙周膜有限元建模探讨 [J]. 口腔疾病防治, 2016, 24(5): 283-287.

[6] 仵健磊，刘云峰，彭伟，等. 基于有限元仿真的形状记忆聚合物弓丝初始正畸力分析 [J]. 中国生物医学工程学报, 2016, 35(2), 202-210.

[7] Liao Zhipeng, Chen Junning, Li Wei, et al. Biomechanical investigation into the role of the periodontal ligament in optimising orthodontic force: a finite element case study [J]. Archives of Oral Biology, 2016, 66: 98-107.

[8] Masakazu H, Taiji A, Teruko TY. Computer simulation of orthodontic tooth movement using CT image-based voxel finite element models with the level set method [J]. Computer Methods in Biomechanics and Biomedical Engineering, 2016, 19(5): 474-483.

[9] Anshul C, Maninder SS, Girish C, et al. Evaluation of stress changes in the mandible with a fixed functional appliance: a finite element study [J]. American Journal of Orthodontics and Dentofacial Orthopedics, 2015, 147(2): 226-234.

[10] Qian Yinglian, Fan Yubo, Liu Zhan, et al. Numerical simulation of tooth movement in a therapy period [J]. Clinical Biomechanics, 2008, 23(1): S48-S52.

[11] Hohmann A, Kober C, Young P, et al. Influence of different modeling strategies for the periodontal ligament on finite element simulation result [J]. American Journal of Orthodontics and Dentofacial Orthopedics, 2011, 139(6): 775-783.

[12] Fill TS, Carey JP, Toogood RW, et al. Experimentally determined mechanical properties of, and models for, the periodontal ligament: critical review of current literature [J]. Journal of Dental Biomechanics, 2011, 10:1-9.

[13] 董晶，张哲湛，周国良. 上颌第一磨牙远中移动时牙周膜应力分布的非线性三维有限元分析 [J]. 上海口腔医学, 2015, 24(3): 315-320.

[14] 魏志刚，汤文成，严斌，等. 基于有限元法的牙周膜本构模型研究 [J]. 工程力学, 2009, 26(10): 211-216.

[15] Papadopoulou K, Hasan I, Keilig L, et al. Biomechanical time dependency of the periodontal ligament: a combined experimental and numerical approach [J]. European Journal of Orthodontics, 2013, 35(6): 811-819.

[16] 魏志刚，汤文成，严斌，等. 基于黏弹性模型的牙周膜生物力学研究 [J]. 东南大学学报(自然科学版), 2009, 39(3): 484-489.

[17] Iman Z, Oskui, Ata H. Dynamic tensile properties of bovine periodontal ligament: a nonlinear viscoelastic model [J]. Journal of Biomechanics, 2016, 49(5), 756-764.

[18] Toms SR, Dakin GJ, Lemons JE, et al. Quasi-linear viscoelastic behavior of the human periodontal ligament [J]. Journal of Biomechanics, 2002, 35(10): 1411-1415.