基于动态性能的坐标机桥框立柱结构优化设计

0 引言

移动桥式三坐标测量机，以简单、紧凑、较好的刚度等优点而具有比其它结构形式更为广泛的应用。其中桥框是测量机中最为关键的受力构件，它的强度和刚度直接影响了测量机的精度以及寿命。以往的基于强度的设计计算难以得到最佳的动态性能，无法确保测量机具有最佳的工作性能，在整体重量上以及动态性能上还具有很大的优化空间。因此，对桥框中的部件进行精确、合理、科学的计算对测量机结构设计而言具有十分重要的意义。

在众多的机床与测量设备的结构件性能优化的研究中，多数学者只停留在对结构的单件进行优化，并且优化的方式多是通过类似结构的比对、经验设计等，这样的方式不仅缺乏详细的结构设计流程以及理论依据支撑，而且缺乏对动态性能的分析和优化[1～4]。

现代设计方法中，基于有限元仿真的动态设计方法得到了广泛的认可。它不仅能在设计初期对结构的动静态性能进行分析，还能通过一系列优化算法求解得到设计人员的设计优化目标，大大减少了设计周期，不仅如此，得到的设计结果比传统的静态设计具有更好的动静态特性，结构更加可靠。

1 坐标机桥框动力学分析

1.1 坐标机桥框模型简化

如图1所示为移动桥式坐标机的结构示意图，移动桥框主要由左立柱、右立柱、横梁构成，左右立柱与横梁之间用螺栓连接，立柱与工作台之间采用空气静压轴承润滑。

将坐标机的框架看作为由质量m、弹簧k和阻尼c组成的振动系统，如图2所示，其运动方程为：

其中，[M]为桥框结构的质量矩阵；[C]为桥框结构的阻尼矩阵；[K]为桥框结构的刚度矩阵；x为桥框结构的位移；为桥框结构的加速度阵；为桥框结构的速度向量。

忽略阻尼的影响，即式(1)中的第二项为0，其特征方程为：

对式(2)进行求解，得到n个ω的互异正根ωi（i=1，2，…，n），将其从小到大依次排列分别为系统的各阶固有频率，其值为：

由式(3)中可以看出，各阶固有频率与质量和刚度有十分密切的关系，固有频率可通过改变结构的静刚度与质量来决定。一般而言，固有频率常作为评价结构动态特性的重要参数，固有频率越高，结构的动态性能越好，越不容易发生共振现象，结构也就越稳定。因此在结构设计时往往尽可能将系统的第一阶固有频率值高于环境的激励频率，即ωi可以作为结构动态设计一个优化目标，改善结构的动态性能。

图1 移动桥式坐标机结构图

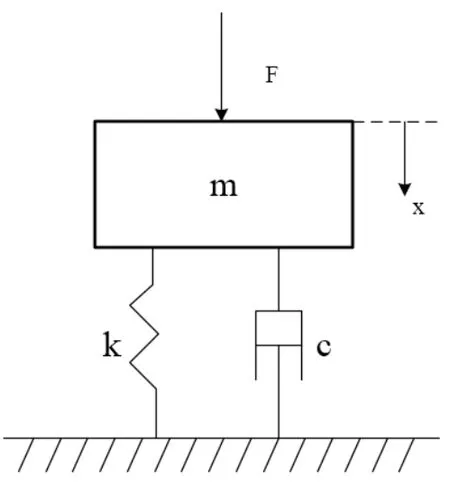
图2 桥框振动系统简图

1.2 坐标机桥框动力学分析

坐标机的实际机构模型中，存在许多微小零件和结构，比如倒角、小孔、圆角、凸台、凹槽和过渡面等，这些结构在网格划分时加大了网格划分难度和工作量，因此将这一部分零件和结构简化处理，减少有限元模型网格划分工作量。而根据圣维南原理，局部结构差异对整体力学性能影响较小，对有限元分析而言影响可以忽略。

坐标机横梁与左右立柱之间采用螺栓连接，立柱与工作台之间采用空气静压轴承润滑，这两个结合面处存在着接触刚度和接触阻尼，它和机械结构的静特性、振动与振动控制及其动态特性都存在着十分密切的关系[5]。因此为了更准确的获得坐标机桥框的动力学分析结果，必须考虑这两个结合面对模态分析的影响。

横梁与立柱之间采用螺栓的固定连接形式，对于螺栓结合面处采用弹簧-阻尼单元进行等效处理，等效刚度采用经验公式计算得到[6]。其结合面动力学模型如图3(a)所示。如图所示，螺栓固定结合面间的采用弹簧-阻尼模型等效模拟螺栓的连接刚度与阻尼。用Kx、Ky、Kz分别表示三个方向的连接刚度，Cx、Cy、Cz分别表示三个方向上的阻尼。如表1所示为根据所选材料与3kN预紧力下的等效模型参数[7]。导轨结合面之间采用空气静压轴承支承，其结合面动力学模型如图3(b)所示。

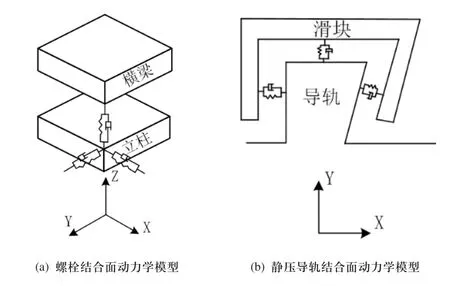
图3 坐标机桥框结合面动力学模型示意图

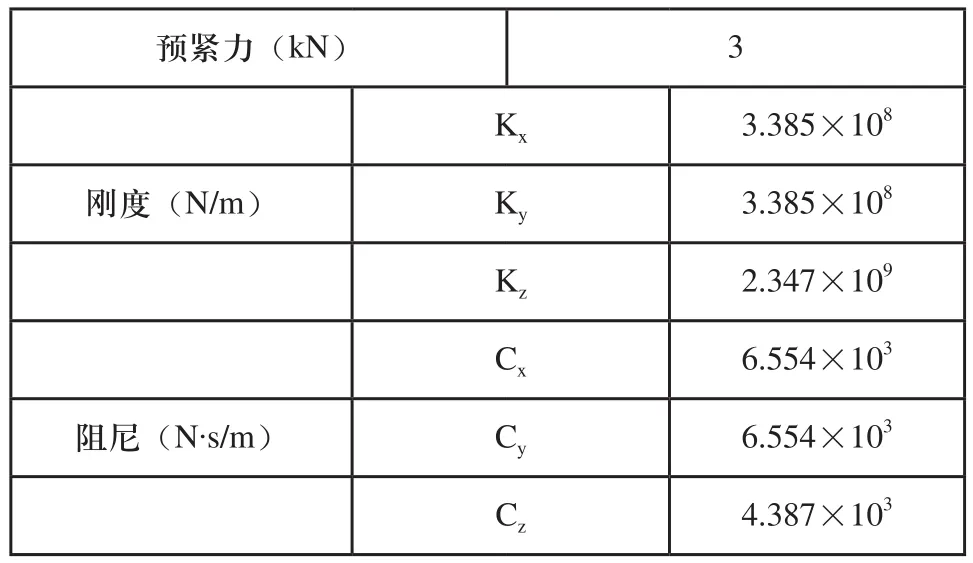
表1 螺栓结合面弹簧单元等效模型参数

坐标机空气静压导轨结合面处主要由气膜提供刚度和阻尼，而阻尼在模态分析时对结构的固有频率和振型不产生影响。因此在对坐标机静压导轨进行有限元建模时，将导轨上的每个滑块与底座之间用弹簧单元代替而不考虑气膜的阻尼影响，弹簧刚度设为静压滑块的承载刚度，从而将静压导轨结合面的刚度等效为弹簧单元刚度[8]。

如表2所示为静压导轨结合面的等效模型参数。

表2 静压导轨结合面弹簧单元等效模型参数

除以上的螺栓固定结合面和静压导轨结合面外，其他结合面采用默认的固结形式，且将相互之间无相对运动的零部件设为多体部件，减少运算量。利用ANSYS Workbench软件对坐标机整机桥框进行模态分析，得到其前六阶固有频率如表3所示，其相应振型如图4所示。

表3 整机前六阶固有频率及振型

由模态分析结果可以看出，坐标机桥框在低阶振动时立柱所表现出的振型变化最为明显，当坐标机与外界激振频率发生共振时，立柱结构的变形对坐标机的整体性能影响最大，因此，对立柱的优化设计对改善整机桥框的动态性能而言至关重要。

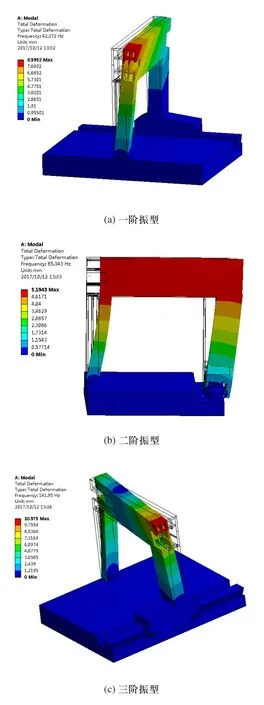
图4 整机前三阶振型

2 桥框立柱的优化设计

对桥框立柱的优化设计分为两个步骤，先对立柱结构进行拓扑优化，确定立柱的基本结构和相关尺寸，再对立柱的尺寸进行参数优化，最终得到最优的设计方案。

2.1 桥框立柱的拓扑优化

结构拓扑优化是在给定的优化设计区域，将结构离散成有限个单元，施加边界条件，结合优化算法，搜寻在设计中材料的最优分布方案[9]。主要的拓扑优化算法有变密度法、均匀化方法、ESO（渐进结构优化法）和水平集方法等[10]。而对于计算机优化而言，仿真软件使用的算法主要为变密度法和均匀化法，本文将采用变密度法对立柱结构进行拓扑优化，将立柱材料的密度作为设计变量，优化目标设为立柱的刚度最大，用立柱结构的变形表述，约束条件设为立柱的体积分数与第一阶固有频率。其拓扑优化的数学模型为[11]：

目标函数：

约束条件：

式中，CW(x)表示立柱对应工况下的总变形；wi为对应工况下的静态应变能；ui(x)为对应工况下节点的位移；K是立柱结构的刚度矩阵；Vi(x)是结构优化后的设计区域体积；V0是结构优化前的设计区域体积；ω1是结构优化后的第一阶固有频率，ω2是结构优化后的第二阶固有频率；xk是第k个单元的密度。

图5为原始模型立柱结构，截面形式为田字型。在进行拓扑优化时将其处理为实心结构，并保持原始尺寸不变。

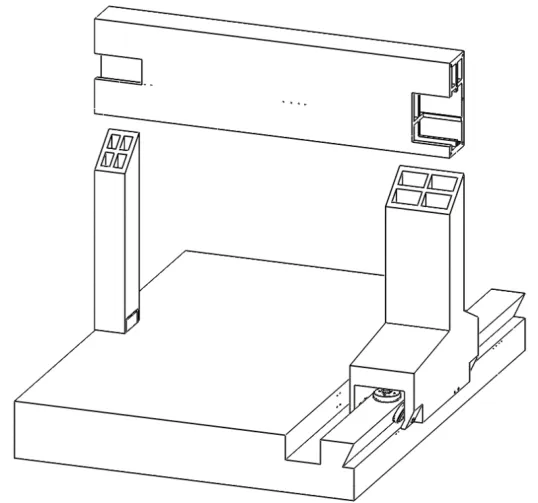
图5 原始设计立柱机构

在对立柱进行拓扑优化之前，应当对模型的设计区域与非设计区域进行划分。如图6所示为已划分好的网格模型。图6中绿色网格部分为拓扑优化设计区域，其他部分为非优化区域。在使用Hyperworks软件中的OptiStruct模块进行优化设计时，软件将根据所设定的优化目标与约束条件对优化区域进行拓扑优化计算。

图6 拓扑优化区域划分示意图

OptiStruct模块优化计算完成后，在HyperView中查看优化结果，设置相关显示参数，只显示伪密度0.3以上的单元，绘制结果如图7所示。

图7 HyperView优化结果等值图

从图7的优化结果可知，实心立柱经优化后形成了明显的C字状，且立柱根部存在两个明显的空洞，右立柱气足连接处的材料分布相对复杂，存在不规则的筋和壁面，内部形成空腔。

2.2 立柱结构参数优化

根据所得到的拓扑优化结果，将新立柱结构的整体框架设计为中空的C字状，壁厚暂定为10mm，由于横梁与立柱间存在螺栓连接，因此保留连接处的实体。在左右立柱根部分别设计一个圆形孔，直径暂定为50mm。右立柱气足处根据拓扑形貌设计成类似的形状。拟定的新立柱设计结构如图8所示。

图8 拟定新立柱设计结构

图8中，t1为左立柱拔模厚度，t2是右立柱拔模厚度，r1为左立柱圆孔半径，r2为右立柱圆孔半径。

各尺寸设计参数范围如表4所示。

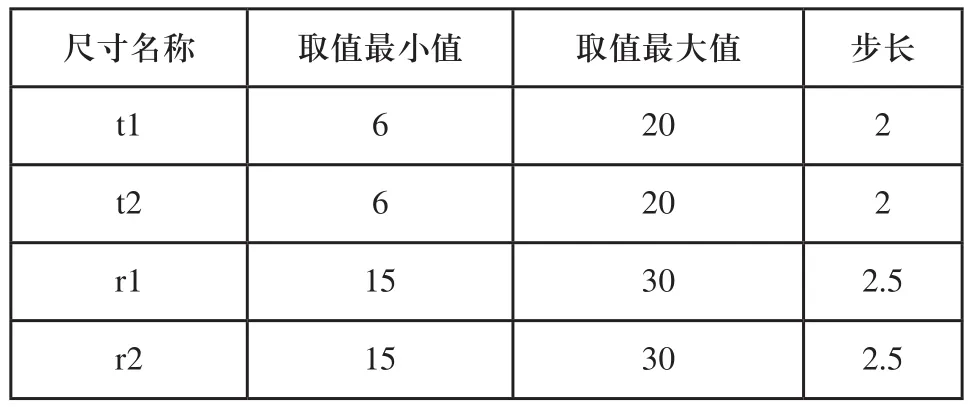
表4 尺寸设计参数取值范围表

运用ANSYS workbench软件对表中各参数进行立柱结构模态分析，得到各参数下桥框立柱结构的一阶固有频率，结果如图9所示。

由图9可知，随着壁厚的增加，桥框立柱结构的一阶固有频率呈小幅度的上升趋势，同时，立柱的质量也在不断上升，然而气浮轴承刚度随着负载变化而发生变化，所选取尺寸应考虑到气浮轴承承载因素。对图9(a)中的一阶固有频率与拔模厚度曲线进行求导，可知，拔模厚度在12mm时取得最佳综合性能。因此，取t1=t2=12mm。r1与r2尺寸对桥框立柱结构的一阶固有频率影响不明显，由图9(b)可知，当r1与r2都取25mm时存在小幅度的突降，一阶固有频率随r2从22.5mm处起明显低于平均值，r1变化对桥框立柱的一阶固有频率影响较小。考虑立柱开孔的加工工艺性与对固有频率的影响，选择开孔尺寸为r1=r2=22.5mm。

图9 各尺寸参数对一阶固有频率影响图

3 优化结果验证

下文对优化前后结构的性能进行对比验证。优化结果从质量、横梁中间位置负载情况下形变量、立柱固有频率三个方面进行验证。结果如表5所示。

表5 桥框立柱结构优化前后性能对比表

从表5所示的结果可以看出，桥框立柱结构在优化之后其总质量得到了明显的减少，总质量相对减少了20.5%。然而优化后的结构由于去除了原结构中的加强筋，使得其在负载静力下的形变量对比原结构略微有所上升，但是对于整体而言基本可以忽略不计。优化前后立柱性能变化最为明显的是其一阶固有频率，从原来的42.372Hz提升到了68.13Hz，相比提高了60.79%；桥框立柱结构的二阶固有频率也从原来的85.343Hz提升到了114.38Hz。

因此，从对比结果上来看，优化后的桥框立柱结构相比较原结构而言具有明显的性能提升，一方面大大减少了结构的质量，减少了材料成本；另一方面明显提升了结构的固有频率，提高了桥框整体的抗干扰能力。

4 结论

1）通过对坐标机桥框结构进行模态分析，其中考虑到了桥框结构各部件间的结合面刚度对整机模态的影响，使得模态分析结果尽可能接近真实情况。模态分析结果显示立柱结构振型变化对坐标机桥框的整体性能影响最大，因此将立柱结构确定为优化对象。

2）通过对立柱结构进行拓扑优化，得到了立柱的概念模型和传力路径，根据对概念模型的单元化处理得到了立柱结构的初步设计方案。

3）根据拓扑优化得到的立柱初步设计方案对立柱结构进行详细的尺寸优化设计，主要设计参数为立柱拔模厚度与立柱根部开孔半径，通过分析各设计参数对桥框模态的影响，综合考虑了负载对气浮轴承的承载特性，得出了合理的设计参数。对尺寸参数优化设计后的桥框结构进行静力学分析与模态分析，将其与原结构各性能指标进行对比，结果显示，立柱结构整体质量下降了20.5%，一阶固有频率上升了60.79%，二阶固有频率上升了34.02%，表明此次结构优化设计明显地提升了桥框结构的整体性能，也表明先对结构拓扑优化再进行尺寸参数优化的设计方法比传统的经验设计方法具有明显的优势。

参考文献：

[1]刘成颖,谭锋,王立平,等.面向机床整机动态性能的立柱结构优化设计研究[J].机械工程学报.2016(03):161-168.

[2]辛志杰,徐燕申,满佳,等.基于有限元分析的数控铣齿机立柱动静态设计[J].中北大学学报,2006,27(6):484-486.

[3]张学玲.基于广义模块化设计的机械结构静、动态特性分析及优化设计[D].天津大学,2004.

[4]郭垒,张辉,叶佩青,等.基于灵敏度分析的机床轻量化设计[J]. 清华大学学报,2011,51(6):846-850.

[5]张学良,徐格宁,温淑花.机械结合面静动态特性研究回顾及展望[J].太原重型机械学院学报.2002(03):276-281.

[6]米洁,杨庆东,郑孝.基于结合面的高精度数控磨床动态特性[J].机械设计与研究.2015(01):93-95.

[7]方兵.精密数控机床及其典型结合面理论建模与实验研究[D].吉林大学,2012.

[8]刘一磊.超精密机床液体静压导轨静动态特性分析及模态参数识别[D].哈尔滨工业大学,2010.

[9]肖齐.加工中心立柱结构优化设计与静压导轨分析[D].大连理工大学,2014.

[10]Bends E M P,Kikuchi N. Generating optimal topologies in structural design using a homogenization method[J].Computer Methods in Applied Mechanics and Engineering.1988,71(2):197-224.

[11]张胜兰,郑冬黎,郝琪,等.基于HyperWorks的结构优化设计技术[M].机械工业出版社,2007.