2017年数学文化高考题赏析及教学建议

王国学

中图分类号：G633.6文献标识码：B文章编号：1672-1578（2018）02-0189-02

数学文化体现了数学的人文价值和科学价值，渗透数学文化的命题能增加中华优秀传统文化的内容，积极培育和践行社会主义核心价值观，充分发挥命题的育人功能和积极导向作用。《普通高中数学课程标准》提出对数学文化的学习要求是数学课程应适当反映数学的历史、应用和发展趋势， 及数学对推动社会发展的作用。2017年修订的高考数学考试大纲提出加强数学文化考查的要求并在高考中得到了体现。下面就以2017年渗透数学文化的高考试题作一赏析。

例1 （2017年高考数学全国Ⅰ卷理科第2题）如图，正方形ABCD内的图形来自中国古代的太极图。正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称。在正方形内随机取一点，则此点取自黑色部分的概率是（ ）。

A.14B.π8C.12D.π4

太极图是以黑白两个鱼形纹组成的圆形图案， 俗称阴阳鱼。太极是中国古代的哲学术语， 意为派生萬物的本源， 太极图形象化地表达了阴阳轮转、相辅相成是万物生成变化根源的哲理。本题在编拟过程中在阴阳鱼的外围增加了正方形， 意在暗喻中国古代天圆地方的理念。试题以此为情境， 设计几何概型以及几何概率计算问题， 体现中国古代传统文化， 同时试题贴近考生生活， 通过本题的求解， 使考生感受中华传统优秀文化的民族性与世界性。

例2 （2017年高考数学全国Ⅱ卷理科第3题）我国古代数学名著《算法统宗》中有如下问题："远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？"意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（ ）。

A.1盏B.3盏C.5盏D.9盏

本题开宗明义地引入我国古代数学名著《算法统宗》， 然后通过诗歌提出数学问题， 阐明试题的数学史背景，激发考生对中华民族优秀传统文化的喜爱。《算法统宗》是我国明代数学家程大位的名著， 是我国珠算史上的一个里程碑。书中的文字浅显易懂， 由浅入深， 试题中的诗句背景源自古代社会生活中常见的7层塔， 同时引入了一个等比数列的相关问题。本题展示了数学的知识和思维方式等在中国古代社会、生活等的广泛渗透和应用， 对引导学生树立数学应用意识具有积极的意义。

例3 （2017年高考数学全国Ⅰ卷理科第8题）下面程序框图是为了求出满足3n？2n>1000的最小偶数n，那么在和两个空白框中，可以分别填入（ ）

A.A>1 000和n=n+1B.A>1 000和n=n+2

C.A 1 000和n=n+1D.A 1 000和n=n+2

本题巧妙地设置了两个空白框中的不等式和等式作为选择题的提问，考查考生对程序框图基本逻辑结构以及对算法语句的含义的理解程度， 从而揭示了数学知识是如何解决具体数学问题的过程， 体现了数学的创造性。

例4（2017年高考数学浙江卷第11题）我国古代数学家刘徽创立的"割圆术"可以估算圆周率π，理论上能把π的值计算到任意精度，祖冲之继承并发展了"割圆术"，将π的值精确到小数点后七位，其结果领先世界一千多年，"割圆术"的第一步是计算单位圆内接正六边形的面积S6，则S6=_____。

数学家刘徽用割圆术求出圆周率是3.141024。除了数学家刘徽还有我国伟大的数学家祖冲之计算出圆周率在3.1415926和3.1415927之间，是世界上第一个把圆周率的值的计算精确到七位小数的人，比国外数学家得出这样精确数值的时间，至少要早一千年。随着科学技术的迅速发展，人们利用电子计算机可以算出小数点后上亿位……

刘徽的 "割圆术"在人类历史上首次将极限和无穷小分割引入数学证明，成为人类文明史中不朽的篇章。 "割圆术"是当时计算圆周率的比较先进的算法，至今仍有一定的应用价值。它体现了以直代曲、无限趋近、"内外夹逼"的思想，这些思想是人们在解决数学问题时最基本、最朴素的思想，在其他领域也有着广泛的应用。"割圆术"这个算法本身很有趣，操作性强，"算理"明确，能被翻译成计算机程序上机运行，体现了中国古代数学的算法特征及辉煌成就。对激发学生的民族自豪感和爱国精神，培养追求科学真理和创新精神有积极意义。

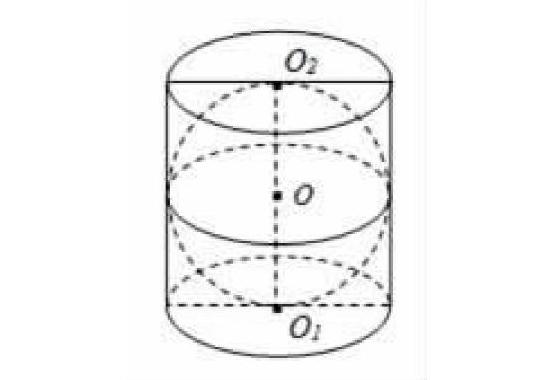
例5（2017年高考数学江苏卷第6题）如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切，记圆柱O1O2的体积为V1，球O的体积为V2，则V1V2的值是______。

阿基米德的墓碑上刻着一个圆柱，圆柱内有一个内切球，这个球的直径恰好与圆柱的高相等.圆柱的体积与球的体积之比以及圆柱的表面积与球的表面积之比均为3：2（即本题答案），相传这个图形表达了阿基米德最引以自豪的发现。

数学学科蕴含着丰富的审美因素，具有极高的美学价值，且有以下四个方面的表现形式：对称美、简洁美、和谐美、奇异美。本题即是以古希腊数学家阿基米德的墓碑文为数学文化背景，体现数学的美。

例5 （2017年高考数学全国Ⅰ卷理科第19题）为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸（单位：cm）。根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N（μ，σ2）。（1）假设生产状态正常，记X表示一天内抽取的16个零件中其尺寸在（μ-3σ，μ+3σ）之外的零件数，求P（X≥1）及X的数学期望;

（2）一天内抽检零件中，如果出现了尺寸在（μ-3σ，μ+3σ）之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查。

（ⅰ）试说明上述监控生产过程方法的合理性;

（ⅱ）下面是检验员在一天内抽取的16个零件的尺寸：

经计算得 ，，其中xi为抽取的第i个零件的尺寸，。

用样本平均数作为μ的估计值，用样本标准差s作为σ的估计值 ，利用估计值判断是否需对当天的生产过程进行检查？剔除之外的数据，用剩下的数据估计μ和σ （精确到0.01）。附：若随机变量Z服从正态分布N（μ，σ2），则P（μ-3σ

本题的背景是产品制造中的质量管理过程。无论产品质量， 还是生产过程的状态都存在着波动， 统计方法能够对这些波动的状况和相关关系进行定量分析， 因此是管理、改进产品质量非常有用的工具。本题据此设计了依据3σ原理、根据产品质量指标的波动情况对生产过程作出判斷。试题循序渐进， 逐步把统计思想融入试题中， 完整地展示了在面对实际数据问题时， 如何利用所学数学知识、数学思想解决问题的过程， 体现了数学知识和原理在现代社会中的应用。

纵观近几年高考试题不难发现数学文化在高考中的体现非常明显， 2015年全国新课标一卷理科第6题和新课标二卷理科第8题分别是"九章算术"和"更相减损术";2016年新课标二卷的"秦九韶算法";在之前的地方性高考试题中也有上海湖北等地的"竹九节问题"和"祖堩原理"等。这类渗透数学文化的命题，不仅将数学知识、思想方法、数学精神融为一体，体现了数学学科对学生核心素养的考核，以及对学生的理性思维能力和创新应用能力的考核。因此，在平时的教学中，我们教师应该：

（1）要多阅读数学史和数学名著，深入挖掘材料背后所隐含的教学价值，全面提高自身的数学修养，把名著中体现的适合教学的相关专业知识、数学史知识、数学的人文精神等提取出来，运用到数学教学工作中去。

（2）要有意识的去锻炼学生的数学阅读能力和数学化能力，以便使学生在考试中能够从这些富含文化背景的题目上快速理清楚题目的核心条件与核心问题。

（3）把课堂上或书本中的数学知识灵活地延伸到实际生活中，多向学生介绍数学在实际生产生活中的广泛应用，鼓励学生多留意数学在日常生活和科学技术上的应用事例。

（4）适时地引导学生去发现数学的美，并让学生在学习中不断感悟数学所呈现出来的美，增强学生兴趣的同时，让学生认识到数学并不仅是计算的工具，更是一种美，一种文化的集合，使学生在逻辑算术的熏陶中获得一种深层的理性文化素养。

总之，一线教师应时刻树立数学文化意识，让学生不仅了解祖先的聪明智慧，增强民族自豪感，也让学生了解数学知识背后丰富的历史渊源，感受数学文化的熏陶，体会数学独特的文化魅力。