电加热服装中加热片与织物组合体的稳态热传递模拟
陈 扬, 杨允出,, 张艺强, 范艳娟, 金艳苹
(1. 浙江理工大学 国际教育学院, 浙江 杭州 310018; 2. 浙江理工大学 浙江省服装工程技术研究中心, 浙江 杭州 310018)
电加热服装可为生活、工作在低温环境下的人们提供热量,降低人们的冻伤风险,已经引起越来越多学者的关注[1-3]。Park等[4]通过暖体假人测试,研究了冬季多层服装系统中电加热片位置对加热效率和有效热阻的影响。Sandra等[5]通过建立仿真模型,研究了加热片在电热登山手套中的位置对其热传递性能的影响。
另外,许多文献对无内部热源的多层织物集合体热传递性能进行实验分析为有内部热源的电加热服装的热舒适性研究提供参考。早在1991年,石巍等[6]研究了多层针织物间的温度梯度的分布情况,结果表明多层针织物间温度梯度分布服从指数曲线的变化规律。庞方丽等[7]认为纤维的导热系数对织物的热传递有显著影响。邹文静[8]将3种不同织物两两组合放置在靠近热源处,来模拟人体着多层服装时的热传递,结果表明当导热系数大的织物靠近热源的时候,保温效果比较好。本文选择3种导热系数不同的织物进行研究。也有文献对无内部热源的织物热传递性能进行建模仿真。孙玉钗等[9-11]利用有限元软件模拟棉织物的热传递过程,揭示了动态热量传递过程中棉织物横截面任意位置、任意时刻温度分布情况,指出空气层层数越多,外层织物表面温度越低。
本文在多层织物热传递理论基础上,用有限元软件对加热片、空气层与不同织物的组合体建立简化三维模型,进行稳态传热模拟,研究有内热源时织物组合体内部和表面的温度场分布特征,以期为冬季电加热服装的设计优化提供参考。
1 传热理论研究
在不考虑湿传递的情况下,热量传递方式有传导、对流和辐射3种。本文主要考虑织物内热传导和织物与空气间热对流2种传热方式。
2层织物间嵌入加热片后,将形成加热片、空气与织物3种材料的组合体,如图1(a)所示,横截面如图1(b)所示。

图1 织物组合体简化模型Fig.1 Simplified model of fabrics system. (a) Fabrics system; (b) Cross section of fabrics system
假设模型的边界为绝热体,和环境没有热交换,对流换热仅存在于织物表面。在该模型传热过程中,同时存在导热和对流。对于加热片,在稳态条件下内部产生的热量Q被分解成2部分:一部分热量Q1先传递至组合体中间的空气层区域,再传递到织物;另一部分热量Q2以导热的方式直接传递给织物;最后Q1和Q2以对流换热的方式传递给外界环境。根据能量守恒定律,热量传递达到稳态时,有:
Q=Q1+Q2=Sh(Ts-Tb)
式中:Q、Q1、Q2为热流量,W;S为织物上下2个面的表面积,m2;h为对流换热系数,W/(m2·K);Ts为织物外表面温度,K;Tb为外界环境温度,K。



图2 织物材料三维热传递Fig.2 Three-dimensional heat transfer of fabric material
对于空气层微元体与织物微元体,导入微元体的总热量应等于微元体的导出热量,其温度场控制方程式为
2 数值模拟
2.1 几何模型
参考人体背部尺寸,给定织物尺寸为30 cm × 30 cm和加热片尺寸为7 cm × 12 cm,设置的织物和加热片的相对位置如图3所示。这里加热片设定2种:一种是均匀的恒温加热片,见图4(a);另一种是加热区域呈纵向条纹嵌在加热片中,见图4(b)。根据实验的对称性,为简化计算,取织物试样1/4部分,加热片、空气层、织物组合体的简化截面如图1(b)所示,在ANSYS中建立的加热片2、空气层、织物组合体的几何模型,如图5所示。

图3 织物与加热片的尺寸及相对位置Fig.3 Dimensions and relative positions of fabrics and heating units
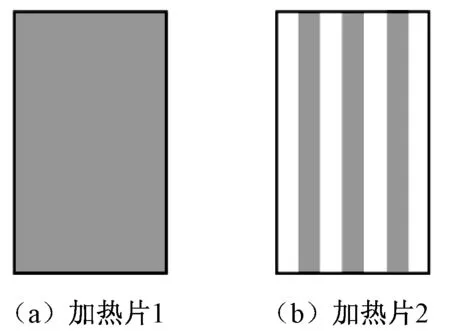
图4 加热片及发热区域Fig.4 Heating units 1 (a) and 2 (b) and heating areas

图5 加热片2与织物组合体的几何模型Fig.5 Geometric model of fabric system with heating unit 2
选用的单元类型为Solid70,具有8个节点,每个节点只有1个温度自由度。该单元可实现匀速热流的传递,适用于三维稳态或瞬态的热分析。对几何模型进一步采用自由网格划分,网格单元尺寸设置为0.002 m。图6示出划分后的部分网格模型,共有115 729个单元,26 331个节点。

图6 部分网格模型Fig.6 One part of mesh model
2.2 材料属性
为简化问题,将织物与加热片作为匀质平板材料。模拟过程选用3种织物,每个模型的上下层均设定为同一种织物,织物试样的相关属性参数如表1所示。加热片厚度为1 mm,空气厚度为1~5 mm,空气的导热系数为0.026 W/(m·K)。

表1 织物参数Tab.1 Fabric parameters
注:1号织物成分为80%羊毛和20%涤纶; 2号织物成分为100%涤纶; 3号织物成分为93%涤纶和7%氨纶。
2.3 施加载荷与边界条件
几何模型网格划分后,对其施加各种约束与载荷。本文模拟的是稳态热传递,需对加热片施加温度载荷,温度载荷值设定为40 ℃,根据市场上现有电热服装的调查结果可知,一般电热服的最高加热温度为40~50 ℃。假定织物的边界是绝缘体,即和环境没有热交换,仅上下表面与空气存在对流,对其施加对流载荷,载荷值为10 W/(m2·K),选择冬季的环境温度来进行讨论,织物周围环境温度设定为10 ℃。
3 结果与分析
3.1 不同织物的热传递模拟
选用加热片1,对不同的织物模型进行稳态热分析,织物厚度见表1,空气层厚度为1 mm,对其施加载荷与求解,其中羊毛呢织物模型的表面和截面温度分布如图7所示。3种织物模型的表面AB线上、横截面CD线上的各节点温度曲线如图8所示。AB线与CD线所在的位置见图1(b)。

图7 羊毛呢织物模型的温度分布云图Fig.7 Temperature distribution nephogram of wool fabric model
由图8(a)可知,不同织物表面AB线上各节点处温度变化趋势基本相同,温度场沿径向呈中间高,两端低分布。其中加热片周围过渡区的温度变化为曲线形状,主要由于加热片边界位置热量沿x-y平面方向和厚度方向多维传递。3种模型中加热片热量沿x-y平面方向传递距离受织物热阻的影响,热阻小的传递距离相对较远。由图8(b)可知,不同织物模型上CD节点处温度变化趋势均为线性变化趋势,因为加热片的中心位置、周围温度条件一致,热量仅沿厚度方向向织物表面进行一维传递。贴着加热片位置处,摇粒绒织物、羊毛呢织物、太空棉织物表面温度分别为31.667、33.208、33.415 ℃,即热阻小的织物表面温度较高。
3.2 不同加热片的热传递模拟
以羊毛呢织物为例,分别选用加热片1和2对羊毛呢织物模型进行稳态热分析,羊毛呢织物厚1.21 mm,空气层厚度为1 mm,对其施加载荷与求解,得到2种模型温度分布云图及AB线上的节点温度曲线图,如图9所示。

图9 2个模型温度分布云图及AB线上节点处的温度Fig.9 Temperature distribution nephograms of two different models and nodal temperature on line AB of two models. (a) Temperature distribution nephogram of model with heating unit 1; (b) Temperature distribution nephogram of model with heating unit 2; (c) Nodal temperature curves on line AB
2个模型中,加热片1和2的几何尺寸相同,发热区域面积不同,加热片2的发热面积为加热片1的3/7。通过分散布置发热区域,可增大加热片四周边界的接触面积,从而提高模型平面内的热量传递。由图9可知,使用加热片1模拟得到的织物表面受热温度均匀,温度维持在33.208 ℃。使用加热片2时,发热区中心位置的织物表面温度与加热片1相同,但2个发热区的中间,温度曲线出现波谷,温度逐渐下降至17.821 ℃,比发热区的最高温度低15.387 ℃,比环境温度高7.821 ℃。
3.3 不同空气层的热传递模拟
以羊毛呢织物为例,模拟稳态热传递,织物厚度为1.21 mm,空气层厚度在1 ~ 5 mm区间变化。对其施加载荷与求解,羊毛呢织物不同模型的表面和截面温度分布如图10(a)、(b)所示。

图10 空气层厚度不同时模型温度分布云图及AB线上节点处的温度Fig.10 Model temperature distribution nephogram of different thickness air layer and nodal temperature on the line AB. (a) Temperature distribution nephogram of model with 3 mm air layer; (b) Temperature distribution nephogram of model with 5 mm air layer; (c) Nodal temperature curves on line AB of models with air layers of different thicknesses
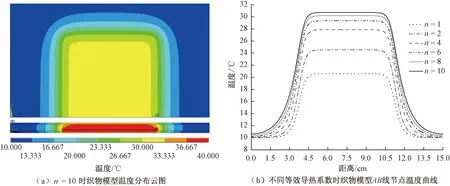
图11 λe不同时模型温度分布云图及AB线上节点处的温度Fig.11 Model temperature distribution nephograms with different value of λe and nodal temperature on the line AB. (a) Temperature distribution nephogram of fabric models with n=10; (b) Nodal temperature curves on line AB of fabric models with different equivalent thermal conductivityies
不同厚度空气层时,织物外表面AB线上节点温度变化如图10(c)所示,各温度曲线最高值分别为33.208、27.886、24.55、22.262、20.596 ℃。随着空气厚度的增大,有加热片处各模型织物外表面温度逐渐降低,且下降幅度逐渐变小。空气层厚度从1 mm增加到2 mm时,曲线最高温度值下降了5.322 ℃,而从4 mm增加到5 mm时的温度差为1.666 ℃。随着空气层厚度的增大,加热片热量沿厚度方向的传递距离逐渐变小,而沿织物x-y平面方向传递距离逐渐变大(见图10(a)、(b))。
3.4 空气层等效导热系数对模型的影响
服装穿着在人身上时,与人体不是紧贴着,衣下空气层内不可能完全静止。由于本文实验模型为局部加热,空气层内微气候各区域温度差值较大,可能同时存在传热、对流、辐射现象。这里假设通过增大空气的等效导热系数,来补偿空气层内的对流、辐射传热。
以羊毛呢织物为例,织物厚度为1.21 mm,空气层厚度为5 mm,将原空气层导热系数λ乘以修正系数n,得到等效导热系数λe=nλ。取n=2, 4, 6, 8, 10;λ=0.026 W/(m·K),进行模拟实验,以便探索织物组合体的温度分布情况。当n=10,即λe=0.26 W/(m·K)时,织物外表面与横截面温度分布云图如图11(a)所示,不同空气层等效导热系数时,提取的织物外表面AB线上节点温度变化如图11(b)所示。
由图10(b)、11(a)可知,随着织物间空气层等效导热系数的增大,加热片热量沿厚度方向的传递距离逐渐变大,沿织物x-y平面方向传递距离也逐渐变大,温度梯度更加明显。图11(b)中,各温度曲线最高值分别为20.596、24.55、27.886、29.366、30.202、30.739 ℃。随着n值的增大,有加热片处各模型织物外表面温度逐渐升高,且升高幅度逐渐变小。修正系数n从1增大到2时,曲线最高温度值上升了3.954 ℃,而从8增大到10时的温度差为0.537 ℃。
4 实验验证
为验证模拟的有效性,在人工气候室中进行了实验,室内温度设定为10 ℃,自然对流。实验所用的3种织物参数见表1。实验设备包括PT100型温度传感器,KSN-3050型可调电源,1 ~ 5 mm厚的亚克力板、温度控制器。调整电源电压,温度控制器设置为40 ℃,使加热膜温度维持在(40±0.5)℃;亚克力板的中间挖掉30 cm×30 cm的正方形来模拟空气层的厚度。实验时,织物、加热片、空气层按照图1(b)的顺序放置,将温度传感器的触头放置在织物表面来记录织物外表面的温度。每组实验做3次,结果取其平均值。不同模型、不同空气层时,织物外表面的平均温度随时间变化曲线图如图12所示。

图12 模型织物外表面温度随时间变化曲线Fig.12 Variation of surface temperature with time of fabric. (a) Different fabrics; (b) Different air layer thicknesses
传热达到平衡时织物外表面的测试温度与模拟数据如表2所示。实验数据与模拟数据的最大相对误差为9.7%,说明织物模型的稳态热传递模拟结果与实际实验具有良好的吻合性。实验中加热片温度的轻微波动,对对流换热系数的确定可能存在误差,其和织物表面的粗糙程度,空气流速等因素相关,因此理论数据和实验数据存在一定的偏差。
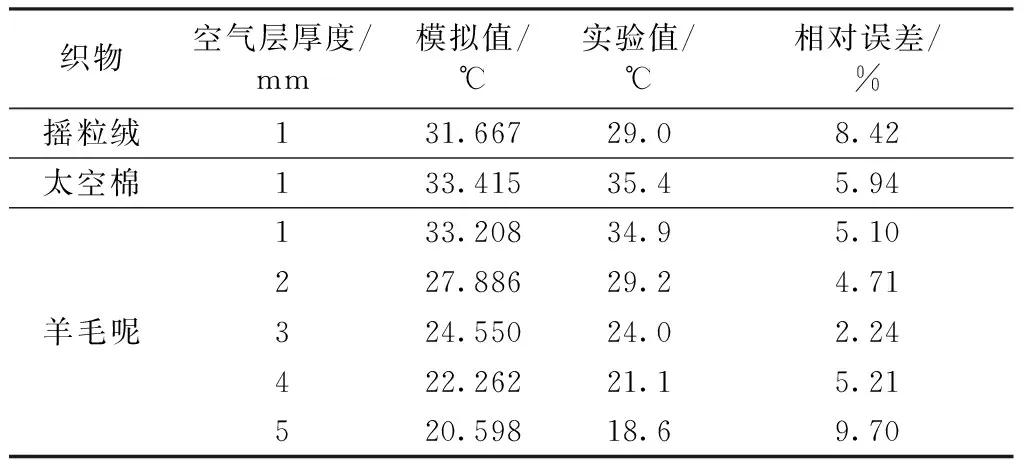
表2 模拟数据与实验数据对比Tab.2 Comparison of simulated data and experimental data
5 结 论
1)通过ANSYS建立加热片、空气层与织物3层组合体的三维有限元模型,可提取出织物表面、横截面任意位置的稳态温度分布情况。
2)织物热阻、空气层厚度对加热片热量在模型中x-y平面和厚度方向的传递有影响。提高织物热阻或增加空气层厚度,则沿厚度方向的热量传递逐渐下降,且下降梯度逐渐变小,而沿织物x-y平面方向热量传递距离变大。
3)通过分散发热区域,可提高模型x-y平面内的传热量。根据环境条件、组合体材料的物理性质、加热片的温度及发热量合理优化发热区域的间隔距离,控制间隔区域的温度分布。
4)考虑空气层复合传热情况时,可通过修正空气层的等效导热系数实现模拟。增加空气层等效导热系数,模型中沿x-y平面方向和厚度方向的热量传递距离均有所增大。
参考文献:
[1] SONG Wenfang, WANG Faming, ZHANG Chengjiao, et al. On the improvement of thermal comfort of university students by using electrically and chemically heated clothing in a cold classroom environment[J]. Building and Environment,2015, 94(2): 704-713.
[2] 赖丹丹, 宋文芳, 王发明. 冷环境下化学加热和电加热服装舒适性能评价[J]. 中国个体防护装备, 2016(2): 40-45.
LAI Dandan, SONG Wenfang, WANG Faming. Comfort performance evaluation of the chemically and electrically heated clothing in a cold environment[J]. China Personal Protection Equipment, 2016(2): 40-45.
[3] 段杏元, 胡源盛. 男士针织内衣热性能的测量与分析[J]. 纺织学报, 2016, 37(12): 92-96.
DUAN Xingyuan, HU Yuansheng. Measurement and analysis on thermal properties of men′s knitted underwears[J]. Journal of Textile Research, 2016, 37(12): 92-96.
[4] PARK H, HWANG S K, LEE J Y, et al. Impact of electrical heating on effective thermal insulation of a multi-layered winter clothing system for optimal heating efficiency[J]. International Journal of Clothing Science and Technology, 2016, 28(2): 254-264.
[5] COUTO S, CAMPOS J B L M, MAYOR T S. On the performance of a mitt heating multilayer: a numerical study[J]. International Journal of Clothing Science and Technology, 2011, 23(5): 373-387.
[6] 石巍, 杨善同. 关于多层针织物间温度梯度的研究[J]. 中国纺织大学学报, 1991, 17(4): 19-24.
SHI Wei, YANG Shantong. On the temperature gradient between knitting fabric layers[J]. Journal of China Textile University, 1991, 17(4): 19-24.
[7] 庞方丽, 刘星, 王瑞. 织物热传递性能的影响因素[J]. 轻纺工业与技术, 2013(2): 21-24.
PANG Fangli, LIU Xing, WANG Rui. Influence factor of fabric heat transfer performance[J]. Textile Industry and Technology, 2013(2): 21-24.
[8] 邹文静. 非稳态条件下纺织品热传递性能[D]. 上海: 东华大学, 2008: 45-47.
ZHOU Wenjing. Researeh of experimental method of textile material performance on unsteady-state thermal transfer[D]. Shanghai: Donghua University, 2008: 45-47.
[9] 孙玉钗, 冯勋伟, 程中浩. 空气层及织物层数对通过纺织品热量损失的影响[J]. 纺织学报, 2005, 26(2): 74-76.
SUN Yuchai, FENG Xunwei, CHENG Zhonghao. Effect of air and fabric layers on heat loss through textile system[J]. Journal of Textile Research, 2005, 26(2): 74-76.
[10] 孙玉钗, 冯勋伟, 刘超颖. 纺织品热传递有限元分析[J]. 东华大学学报(自然科学版), 2006, 32(2): 50-53.
SUN Yuchai, FENG Xunwei, LIU Chaoying. Application of finite element method in analysis of heat transfer through textile fabrics[J]. Journal of Donghua University(Natural Science Edition), 2006, 32(2): 50-53.
[11] SAN Y, CHEN X, CHENG Z, et al. Study of heat transfer through layers of textiles using finite element method[J]. International Journal of Clothing Science and Technology, 2010, 22(2): 161-173.

