大规模MIMO中的迭代匹配滤波算法

张荣升， 许崇斌， 王昕

(复旦大学 信息科学与工程学院，上海 200433)

0 引言

为了满足逐渐增长的数据服务要求，大规模多输入多输出(MIMO)技术已经在5G系统中被提出了[1]，这种场景下一个具有很多天线的基站(BS)同时服务许多用户。当BS的天线数N远大于用户数K的时候，用户的信道变得彼此之间近似正交。对上行链路传输，在基站端利用简单的匹配滤波(MF)接收机就可以获得近似最优的性能。

对于实际的系统，条件N≫K通常是不成立的。在这种情况下，MF接收机会产生明显的性能损失。因为这个原因，更复杂的检测方法，像线性的最小均方误差(MMSE)接收机，更偏向于以一个更高的复杂度来获得更好的性能。基于Neunann级数近似，为了权衡好的性能和可承受的复杂度，一种近似的MMSE(A-MMSE)方案被提出了[2-5]。但是当用户数K很大时，要么A-MMSE复杂度变得很高，要么有不可忽略的性能损失。

在这篇文章里，我们针对大规模MIMO上行链路的符号检测提出了一种迭代的MF(I-MF)方案。提出的方法由一个修正的MF(MMF)和K个解调器(DeMs)组成。与已经存在的方案不同[6-8]，为了获得更好的性能从解调器反馈的软信息被应用到MMF。另一方面来说，与传统的迭代检测不一样的是，仅仅解调器(代替解码端)与迭代相关联，这也带来了低损耗的实现和短暂的延迟。具体来说，基于MMF的输出，DeMs执行了标准的后验解调。利用解调的结果，外信息(以信号均值和方差的形式)反馈给了MMF端来阻止用户之间的相互干扰。然后MMF端提升的输出又一次传给DeMs端。这个过程迭代直至收敛。可以发现较少的迭代次数就可以获得近似最优的性能。并且仅需要低复杂度，提出的I-MF方法甚至本质上能超过高复杂度的MMSE方案。

注意到一个相似的迭代的方法在[9]中被采用，它提出了一种信道硬信息利用传递(CHEMP)的接收机。通过优化权重参数，CHEMP接收机在大规模MIMO系统中表现很好。我们在这篇文章中提出I-MF方法展示了一种不同的信息传递方法，并且我们可以解释提出的方案性能提升的原因。同时提出的方法也可以与存在的AMMSE方案组合来提供一个更好的性能与复杂度之间的权衡。

标记说明：(·)*,(·)H,(·)-1各自表示共轭，共轭转置和矩阵的逆；I是适当大小的单位矩阵；Ε[·]表示统计期望；diag(a)表示对角矩阵，其对角元素是矢量a的元素；{·}表示一个序列。

2 预备知识

2.1 系统模型

考虑一种上行信道，具有大数目N个天线的BS服务于K个单天线用户。那么BS端的接收信号可以表示成式(1)。

(1)

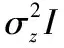
使用H:=[h1,h2,…,hK],h:=[x1,x2,…,xK]T，我们可以以紧凑的形式重写式(1)为式(2)。

r=Hx+z

(2)

在这篇文章中，假设矩阵H中的每个元素都是独立同分布的(i.i.d.)0均值单位方差的复高斯随机变量。

2.2 MMSE接收机

用ux和Vx分别表示传输信号x的先验均值矢量和协方差矩阵。假设Vx是一个对角矩阵diag{[v1,…,vK]}1。则MMSE估计可以由[6]给出式(3)。

(3)

2.2 近似MMSE接收机

为了避免直接A-1计算，[2]-[5]提出了一种A-MMSE方法。把矩阵A分解为A=D+E,其中D是包含矩阵A对角元素的对角矩阵，E是矩阵A去除对角元素的矩阵。则对A-1的Neumann级数近似可由式[2]-式[5]给出式(4)。

(4)

其中L是近似的项数。通过选取合适的L值，当K/N相对小时，A-MMSE能够获得较好的性能复杂度的权衡。

3 提出的迭代MF接收机

当条件N≫K不满足的时候，MMSE和A-MMSE方法都有很高的复杂度并且它们的性能本质上离最优较远。为了达到接近最优的性能并保持低复杂度，提出了新颖的I-MF方法。

如图1所示。

图1 迭代MF(I-MF)接收机

3.1 带反馈信息的修正的MF

用uk,vk表示传输符号xk的先验均值和方差，k=1,…,K，它们由DeM的反馈得到。在第一次迭代中，因为没有反馈，我们简单初始化uk=0,vk=1(假设符号xk在调制星座点S上等概分布，∀k)。

为了估计xk，我们先从(2)中提取中其他用户的均值以去掉干扰。则接受到的信号可更新为2

然后我们应用MF可获得式(5)。

(5)

基于(5)，关于xk的无偏估计可给出式(6)。

(6)

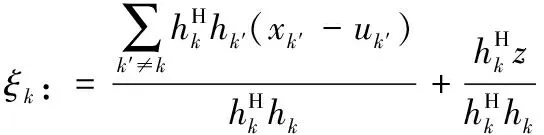
(7)

3.2 解调及反馈信息更新

(8)

(9)

(10)

(10)

3.3 算法和复杂度

利用展现的MMF和DeM，提出的I-MF方法的迭代过程列在算法1中，其中迭代次数Q可以根据性能需要和复杂度约束进行选择。

算法1： 迭代的MF方法(I-MF)

1: Initialization: 初始化迭代数Q，对于k=1,…,K，uk=0,vk=1；

4: Repeat: 重复步骤2和步骤3共Q次。

下面我们比较提出的I-MF方法和其他存在的方法的复杂度，如表1所示。

表1 不同方法的复杂度比较

MF, MMSE, A-MMSE, I-MF的复杂度(i.e.，乘法的次数)。尽管I-MF与MF一样有相似的线性复杂度，但是它本质上性能优于A-MMSE和MMSE。

4 仿真结果

使用QPSK传输符号时，MF，MMSE和提出的I-MF方案BER的性能，如图2所示。

同样我们也提供了最优情况下(单用户无干扰)的性能曲线作为基准。对于I-MF，我们提供了利用算法1迭代1次(Q=1)和迭代4次(Q=4)的性能曲线。

从图2可以看出I-MF的性能仅1次迭代(i.e.，Q=1)就大大超出了MF方法的性能。随着用户数K的增加，达到收敛迭代需要的次数也轻微的增加。这是因为更大的K意味着更大的干扰。通过一个小的迭代次数，提出的方法的复杂度比传统的MMSE小很多。对于K=64，提出的I-MF方法(利用4次迭代，Q=4)相对于MMSE在BER=10-3时有1 dB的性能增益。并且当SNR≥4 dB时它的性能接近单用户的性能。

当用户传输是16QAM时不同方法的性能对比，如图3所示。

图2 QPSK下不同方法的性能

图3 16-QAM下Q=15不同方法BER性能比较

在这种情况下，为了收敛需要更多的迭代次数(Q=15)。这是因为高阶调制时相对于低阶调制提供了更少的信息。(在这种情况下，最优的线性和非线性估计是相同的。)但是提出的I-MF在SNR不太低并保持相对小的复杂度下，仍然能比MMSE性能更好。注意我们还可以通过设计更复杂的均衡器取代MMF(e.g.，使用L>1项的A-MMSE)来提高迭代方案的性能。可以通过合适挑选Q和L值来获得一个性能和复杂度平衡的性能。这超出了这篇文章的范围。

5 总结

我们对于大规模MIMO提出了一种新颖的I-MF方案。提出的I-MF方法以低的复杂度达到近似最优的性能并且明显超出现有存在的方法。鉴于提出的方法的准则，一种用更复杂的均衡器取代MMF通用的迭代方法可以被研究，其可以用可接受的复杂度达到更好的性能。这也将是我们未来的工作。

参考文献

[1] Rusek F, Persson D, Lau B K, et al. Scaling Up MIMO: Opportunities and Challenges with Very Large Arrays[J]. Signal Processing Magazine IEEE, 2013, 30(1):40-60.

[2] Wang F, Zhang C, Yang J, et al. Efficient matrix inversion architecture for linear detection in massive MIMO systems[C]. IEEE International Conference on Digital Signal Processing. IEEE, 2015:248-252.

[3] Müller R, Verdú S. Design and analysis of low-complexity interference mitigation on vector channels[J]. IEEE Journal on Selected Areas in Communications, 2001, 19(8):1429-1441.

[4] Wu M, Yin B, Wang G, et al. Large-Scale MIMO Detection for 3GPP LTE: Algorithms and FPGA Implementations[J]. IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5):916-929.

[5] Rosário F, Monteiro F A, Rodrigues A. Fast Matrix Inversion Updates for Massive MIMO Detection and Precoding[J]. IEEE Signal Processing Letters, 2015, 23(1):75-79.

[6] Sengijpta S K. Fundamentals of Statistical Signal Processing: Estimation Theory[M]. PTR Prentice hall, 1993.

[7] Ping L, Liu L, Wu K Y, et al. On interleave-division multiple-access[C]. IEEE International Conference on Communications. IEEE, 2008:2869-2873 Vol.5.

[8] Guo Q, Huang D D. A Concise Representation for the Soft-in Soft-out LMMSE Detector[J]. IEEE Communications Letters, 2011, 15(5):566-568.

[9] Narasimhan T L, Chockalingam A. Channel Hardening-Exploiting Message Passing (CHEMP) Receiver in Large-Scale MIMO Systems[J]. IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5):847-860.