简化粒子群优化结合SOM的网络入侵检测方法

王红梅

(新疆工程学院 计算机工程系，乌鲁木齐 830011)

0 引言

随着互联网的发展，联网计算机越来越多，网络应用也相应增多。与此同时，网络面临的攻击[1]也日益增多，且网络线性服务也更容易向入侵者和攻击者暴露信息[2]，因此入侵检测系统(Intrusion Detection Systems，IDS)近些年越来越受到研究者们的重视[3]。

一般的网络保护不回应攻击者或入侵者，采用被动的手段减少信息暴露[4]。但是，由于新攻击的复杂性增加，需要更精细的方法来应对，有文献提出通过模式分类区分正常与异常业务[5]，实现对潜在的或实时的攻击进行主动防御，如IDS就是主动防御系统，能够连续监测网络以对业务分类、检测异常行为，并按预定义规则进行响应[6]。这便带出基于特定方法的分类问题，基于特征选择的IDS分析所有输入数据包来检索匹配与入侵相关的模式，即将数据库中的模式与网络业务中提取的模式进行比较以检测出攻击，然而该方法无法检测出数据库中未包含特征值的攻击，而且过期数据库或特征值不足可能会导致漏报或误报[7]。基于异常的IDS通过检索网络是否背离正常模式以确定链接是否异常。同样，基于异常的IDS须要足够精确的模型才能够区分正常与异常模式，否则会产生很多漏报或误报。由于攻击的多样性，有必要计算更复杂的特征以提高检测[8]。

因此，提出利用主成分分析(Principal Component Analysis，PCA)和自组织映射(Self-organizing mapping，SOM)的IDS方法。通过PCA生成非相关性特征用于去除噪声，避免使用低方差变量，并根据判别能力更新特征。而特征空间建模通过概率SOM均值来分类，允许测量每个网络单元的激活概率以检测所有高频率攻击的精确值，运用简化粒子群优化(SPSO)算法从分类搜索当前解的邻域内找到更优的解。实验结果表明，提出的方法具有更高的入侵检测准确率。

1 提出的方法

特征选择是分类问题的关键步骤，因为它有助于消除冗余和不相关输入特征，这不仅能够减少学习时间，还提高了分类精度。基于PCA的特征选择方法，能够提取相关数据集信息，选择主成分投影判别力，并根据最大类分离能力对成分进行排序。

1.1 基于PCA的特征选择

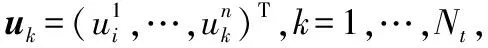
*uk

另外，可以根据主成分重构原始数据：

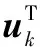
*X

ψ=ψ1,…,ψn中ψi对应于X在特征向量ui的上的投影。由于PCA根据方差递减顺序对特征向量进行排序，则特征向量可根据FDR值排序：

其中σi、μi分别是方差和分类i的均值。

当只使用最大类分离能力的特征向量去除数据集噪声，通过选择具有较低FDR值的投影来实现，即减去基于原始数据集特征向量的重构样本，方程表述为：

1.2 基于SOM映射分类

SOM是最流行的无监督学习神经网络模型，SOM组中相似数据实例化为点阵，即输出映射，不同数据实例将分开输出映射。从而可从输出映射推断出重要的输入空间属性。SOM方法简述如下：

假设X⊂Rn是n维数据流，SOM映射由d个单元构成，每个都由n维模型矢量ωi表示。对于每个输入数据实例v，最佳匹配单元BMU定义为与v最接近的单元ωi：

∀v∈X，i≠j

而线性SOM原型初始化旨在适应训练数据的特征值和特征向量。初始化方法说明原型的第一维度按比例排列为第一主成分，第二维度按比例排列为第二主成分。一旦映射经过训练，每个原型代表输入向量集。当新数据实例展现给SOM时，学习模型激活对应的BMU。

另一方面，通过高斯混合模型(Gaussian Mixture Model，GAMM)[10]建模获得SOM概率表示，从而得到模糊SOM单元响应。再通过SOM单元先验激活概率进一步调整映射响应，允许激活层用于案例中正常连接与网络异常的对应模式。以此判别激活模式是否正常，以检测网络是否异常。基于下列公式构建GMM，其中高斯分量的权重pi对应于先验概率。

Pi(x)是n维高斯分布，作为原型向量，计算得：

每个高斯分量μi的平均值，对应单元本身的原型向量，i组分的协方差矩阵∑i由数据样本围绕模型向量ωi的离散化给定，即每个高斯分量模拟对应单元的接收域分布。一旦构建完成GMM模型，给定输入x的单元k响应，可以用贝叶斯定理计算后验概率[11]，完成对正常连接映射单元和网络异常映射单元的分类。

1.3 简化粒子群优化

为了进一步提高提出的方法的性能，提出简化粒子群优化(Simplified particle swarm optimization，SPSO)[12]并入局部搜索策略，以执行每一代获得的全局最优解。通过SPSO进行粗略搜索，但有时会产生不成熟结果，因此需要嵌入局部搜索策略到SPSO中，以便使SPSO产生更优化的解。局部搜索先从当前解开始，再从其邻域中搜索更优解，一直重复执行邻域搜索直到满足局部最优解。局部搜索的目的是找出粒子的局部最优解PB或当前粒子本身的全局最优解GB。提出的方法中合并了新加权局部搜索方法，加权局部搜索应用于SPSO规则挖掘的加权预定常数是Cw、Cp和Cg，并根据下式使用加权预定变量更新粒子。

为了获得新PB和GB，重新评估粒子的适应值，加权局部搜索算法的步骤如下：

步骤1：预先确定局部搜索时间T和局部搜索权重ω。

步骤2：选择目标粒子Pt。GB将是待运行T次局部搜索的第一目标粒子，依次选择其他PB作为目标粒子，运行T次局部搜索。

步骤3：获取新的3个加权值：(ω*Cw)、(ω*Cp)和(ω*Cg)。

步骤4：根据上式通过新加权值(ω*Cw)、(ω*Cp)和(ω*Cg)更新粒子位置。

步骤5：重新评估目标粒子的适应值。

步骤6：检查适应值是否比目标粒子当前PB或GB更好。若粒子已经得到了新PB，目标粒子局部搜索的迭代将重置为零，重新运行局部搜索，直到局部搜索T次后仍没有找到更多PB，局部搜索过程将停止。

2 实验

实验基于KDDCUP99修订版本数据集[13]，由KDDCup99数据集基于不同概率分布生成训练和测试集。该集包括模拟主机、网络正常流量和人工生成的网络攻击，并移除了冗余记录，根据攻击检测难度对攻击进行标记和排序。KDDCUP99数据集提供了45种网络任务特征以描述各种连接，这些特征总结如下：1.基本特征。总结了所有TCP/IP连接的属性。2.流量特征。包括基于时间窗口计算的特征，以及相应的时间窗口之后，目标端口或服务保持相同的连接信息，KDDCUP99时间窗口设置为2 s。3.基s于内容特征。由于U2R或R2L攻击由在数据包有效载荷上重复发送类似模式构成，因此有必要检查数据包内容以找出攻击。

实验通过KDDCUP99测试集的标签信息对提出的方法与基于特征选择的IDS和基于异常的IDS进行性能评价。并计算入侵检测准确度ACC统计测度来评价各方法的性能，其定义如下：

式中TP、TN、FP和FN分别表示真阳性、真阴性、假阳性和假阴性。

仿真3种常见的网络攻击U2R，DOS和PROB，验证提出的方法的入侵检测准确率，训练阶段和测试阶段分别涉及26 000和28 000条数据。如U2R攻击在训练阶段体现真阳性TP有13 500条、假阳性FP有1 575条、真阴性TN有10 924条、假阳性FN有1条，总计26 000条，因此可计算入侵检测准确度ACC为93.9%。同理，U2R攻击在测试阶段体现真阳性TP有13 200条、假阳性FP有1 862条、真阴性TN有12 934条、假阳性FN有4条，总计28 000条，因此可计算入侵检测准确度ACC为93.3%。以此类推，可分别计算出其他类型攻击检测准确度，如表1所示。

表1 提出的方法训练集与测试集的ACC实验结果

从表1可以看出，提出的方法对于U2R，DOS和PROB三种类型的入侵检测都表现出较好的性能。在U2R的入侵检测中，准确率达93.9%；而在DOS和PROB类型中准确率也分别达到了94.3%和94.2%，由此可见，提出的方法对3种常见的网络攻击U2R，DOS和PROB的入侵检测均表现出了良好的性能,如表2所示。

表2 各方法的ACC性能比较

从表2可以看出，相比于另外两种方法，提出的方法具有更高的入侵检测准确率，这得益于基于PCA的特征选择的噪声去除、SOM的先验激活概率的映射响应调整以及SPSO分类搜索的综合运用。

3 总结

提出一种利用PCA和SOM的IDS方法，采用PCA生成非相关性特征，并根据判别能力更新特征。特征空间建模通过概率SOM均值来分类，并运用简化粒子群优化(SPSO)算法从分类搜索当前解的邻域内找到更优的解。基于KDDCUP99标准数据集和公共数据集搭建仿真测试平台，将提出的方法与基于特征选择的IDS和基于异常的IDS进行性能评价，实验结果表明，提出的方法对三种常见的网络攻击U2R，DOS和PROB的入侵检测均表现出了良好的性能，在

U2R、DOS和PROB的入侵检测中，准确率分别达到了93.9%、94.3%和94.2%，具有更高的入侵检测准确率。

提出的方法可进一步通过不同的SOM单元先验激活概率来修改分类能力，以避免新数据导致的SOM重新训练问题。因此，今后研究可以通过多目标优化来提升先验激活概率的计算能力，通过关联构建层次化模型，以区分正常与异常连接，从而应对数据集中描述的四类攻击。

参考文献

[1] 马磊娟, 王林生. 改进最小二乘支持向量机的网络入侵检测[J]. 微型电脑应用, 2017, 33(7): 76-79.

[2] 蔡思思, 熊国明. 基于MFOALSSVM的IPV6网络入侵检测算法研究[J]. 湘潭大学自然科学学报, 2017, 39(1): 78-81.

[3] Zhou C, Huang S, Xiong N, et al. Design and Analysis of Multimodel-Based Anomaly Intrusion Detection Systems in Industrial Process Automation[J]. Transactions on Systems Man & Cybernetics Systems IEEE, 2015, 45(10): 1-8.

[4] 韩红光, 周改云. 基于Makov链状态转移概率矩阵的网络入侵检测[J]. 控制工程, 2017, 24(3): 698-704.

[5] Derhab A, Bouras A. Multivariate correlation analysis and geometric linear similarity for real-time intrusion detection systems [J]. Security & Communication Networks, 2015, 8(7): 1193-1212.

[6] Aldwairi M, Khamayseh Y, Al-Masri M. Application of artificial bee colony for intrusion detection systems [J]. Security & Communication Networks, 2015, 8(16): 2730-2740.

[7] 王习特, 申德荣, 白梅,等. BOD:一种高效的分布式离群点检测算法[J]. 计算机学报, 2016, 39(1): 36-51.

[8] 李永忠, 陈兴亮, 于化龙. 基于改进DS证据融合与ELM的入侵检测算法[J]. 计算机应用研究, 2016, 33(10): 3049-3051.

[9] Zhou J, Xi-Bing L I, Shi X Z, et al. Predicting pillar stability for underground mine using Fisher discriminant analysis and SVM methods [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(12): 2734-2743.

[10] Layer T, Blaickner M, Knäusl B, et al. PET image segmentation using a Gaussian mixture model and Markov random fields [J]. EJNMMI Physics, 2015, 2(1): 9-13.

[11] 任晓奎, 缴文斌, 周丹. 基于粒子群的加权朴素贝叶斯入侵检测模型[J]. 计算机工程与应用, 2016, 52(7): 122-126.

[12] Kong X, Gao L, Ouyang H, et al. Solving the redundancy allocation problem with multiple strategy choices using a new simplified particle swarm optimization [J]. Reliability Engineering & System Safety, 2015, 144(3): 147-158.

[13] 张新有, 曾华燊, 贾磊. 入侵检测数据集KDD CUP99研究[J]. 计算机工程与设计, 2010, 31(22): 4809-4812.