试析数学实践能力的具体体现

学习数学的价值究竟何在？这是学生经常会问到的问题，也是多数教师难以回答的问题。进入中学阶段后，数学知识逐渐变得抽象起来，似乎与现实世界的需求脱离，学生有这种疑问不足为奇。其实，这是学生未真正认识数学价值所在的表现。笔者认为，数学真正的可贵之处，是在数学的实践之中。借用中科院报告中的一句话： “学科的强大生命力在于对社会进步的贡献，数学也不例外。”因此，拥有一定的数学实践能力，是学生不可或缺的数学素养。

简单来讲，数学实践能力可以分为以下几个方面。

一、综合数学学科内的知识解决问题的能力

数学课程是按照数学的科学体系和学生认知规律进行设计的，其中的数、图、量、形等方面的内容有密切的联系。对学生来说，把握好数学知识的整体性，理解和领会数学知识的内在联系，才能真正把握数学知识的本质，提高解决实际问题的能力。教师应引导学生理解数学知识的内在联系，使学生能有效综合数学知识解决问题，提高其对数学整体性的认识，这是培养学生数学实践能力的第一步。

数学知识的综合应用往往体现在知识的多重理解和使用上。实践中，教师往往通过设置适当的例题促进学生知识的综合。如下列试题：

求函数y=sin2x+2sinxcosx+3cos2x的最小值，并写出使函数取得最小值的集合。

该题主要考查正弦定理、余弦定理，其中还渗透了三角函数式的恒等变形。本题的解答过程中用到了交换律和结合律，平方关系、二倍角正弦公式、余弦公式的逆用，化six2x+cos2x为一个角的三角函数公式，正弦函数y=Asin（wx+ø）的性质：最值及最值点集合等。题目虽然不难，但构建了学科知识的内部联系，考查了学生综合掌握数学知识解决问题的能力。

除了同一范畴内数学知识 （几何或代数）的综合应用，几何与代数综合应用的考查也成了中高考的常态内容。这类题目把代数的基本概念、性质、思想方法与解析几何的基本概念、性质、思想方法等内容融合在一起，大多数题目创意新颖、深刻，是对学生综合数学能力的考查。如下面的试题：

设a、b、c、d都是正数，证明存在一个三角形，它的边长为试计算这个三角形的面积。

学生的解题思路通常是通过证明三个数中最大数小于其他两数之和，从而证得三角形的存在。经过尝试后，发现本题用这一方法很难证明，海伦公式求面积法在此题中也很难运用。

观察三边长的特征，我们很容易注意到，由勾股定理，很容易构造一个边长为a+b，c+d的矩形 （如下图）：

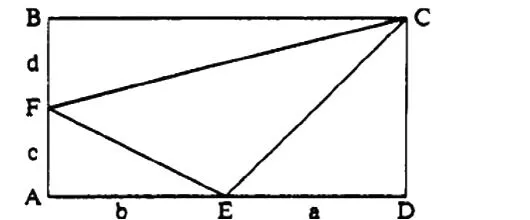
在AD上取E，使AE=b，ED=a；在AB上取F，使由图易知：

这样，我们构造的△EFC就是一个以题中三个数为边长的三角形。其面积为：

这一解题过程，从代数问题到几何问题，又从几何问题回到代数问题，体现了学生综合几何与代数知识，多角度思考和应用数学知识的能力。这样的数学解题过程，是发展学生数学实践能力的基础。

二、将数学知识与其他学科知识结合的能力

数学与其他科学，尤其与自然科学的发展总是相辅相成的。如今，数学的应用几乎渗透到了每一个学科领域中。即使在社会学科、人文学科，也越来越多地用到数学知识及其思想方法。某种程度上来讲，数学是一种通用的科学语言，也是解决其他学科问题的工具之一。

对学生而言，应该该如何结合其他学科知识进行数学实践？这就需要学生以科学的态度看待我们观察到的现象。物理学中数学知识的重要性尤为突出。从最简单的重力加速度的图像 （一元二次方程），到振动图线和波形图，热学中的p-V图、p-T图，以及电学中的I-U图，我们利用数学知识可以分析这些图像，两个物理量用图像表达是什么函数关系，图像的切线、横截距、纵截距、渐近线，图像的斜率、交点，图像与轴所围的面积等分别代表什么含义。将物理条件、物理过程用数学式表达出来，就属于应用数学处理物理问题的能力，即学生在物理学科中进行数学实践的能力。高考物理试题中对学生物理与数学结合能力的考查也频频出现。

再以探究生物现象为例。在寒冷的冬天，猫睡觉时总是把身体缩成一个球形，这样裸露在冷空气中的表面积最小；蜘蛛丝结的八卦网既复杂又美丽，这种八角形的几何图案，即使我们用直尺和圆规也难画得那样匀称。对这些自然现象的探究，就需要运用到数学知识。通过构建合理的数学模型，可以定量地描述生命物质运动的过程，将一个复杂的生物学问题转变成一个数学问题。通过对数学模型的逻辑推理、求解和运算，就能够获得客观事物的有关结论，达到对生命现象进行研究的目的。

三、在日常生活中实践数学的能力

《义务教育数学课程标准 （2011年版）》提出的十大核心词之一 “应用意识”，包含了两个方面：一是有意识利用数学的概念、原理和方法解释现实世界中的现象、解决现实世界中的问题；二是认识现实世界中蕴涵着大量与数量和图形有关的问题，这些问题可以抽象成数学问题，能够用数学的方法解决。学生在生活中进行数学实践，是培养应用意识的基本途径。数学知识与生活实践的结合，也是知与行的结合，学生可从中获得数学素养的提升。

日常生活中的数学实践，首先体现在用数学知识解决生活中遇到的问题上。我们在购物、缴费、贷款时，商家为了提高销售额，往往会提供多种付款方式或优惠方案。作为消费者，要认真对比，仔细分析，学会运用自己掌握的数学知识选择最优惠的方案。此外，在面临某些决策的时候，也需要我们理性地用数学知识来辅助决策。例如：

有三家公司为大学生甲提供应聘机会，按面试的时间顺序，这三家公司分别记为A，B，C。每家公司都可提供 “极好” “好”和 “一般”三种职位。甲获得极好、好和一般的可能概率依次为0.2，0.3和0.4，还有0.1的概率为没有获得职位，即没有工资。三家公司的工资承诺表如下：

?

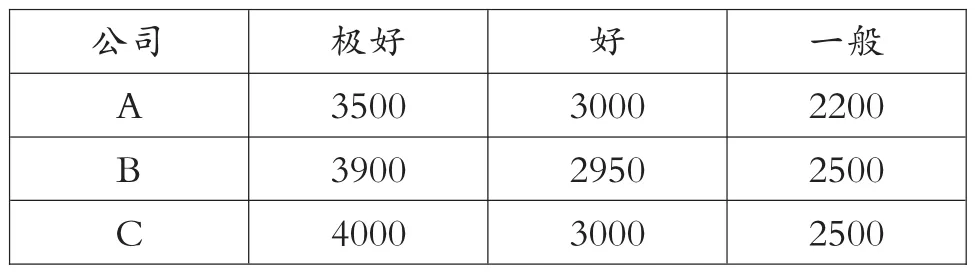
如果甲把工资作为首选条件，那么甲在各公司面试时，对该公司提供的各种职位应作何种选择？

在这一决策问题中，大学生甲必须综合考虑三家公司的待遇问题，对其提供的职务、待遇和自己工作能力来判断决策，比较三个公司提供的哪个职位使自己得到最多的工资待遇，而不是简单地看哪家公司的极好职位工资最高。有了这样的数学实践意识，做出求职决策的时候才不会盲目。

日常生活中的数学实践，还体现在将生活问题数学化上。教师可以通过提供真实可感的生活实例，引导学生掌握从实际生活中抽象出数学问题的方法，让其感受到生活中处处有数学，体验数学学习的重要性。数学知识实践既与学生的课堂学习紧密相连，又可以让学生通过自己的亲身实践，体验到生活中蕴藏的数学知识，从而提高学习数学的热情。

学生在长期的数学实践中，逐步形成数学实践的能力，明确学习数学知识的意义，自然会对探求数学知识产生乐趣。如此，学生科学精神得以梳理，数学能力得到提高，发展数学核心素养才不是一句空话。