六维力传感器解耦综述
王志军,王 凯,刘宣佑
(华北理工大学 机械工程学院, 河北 唐山 063000)
0 引言
在机器人技术领域中,智能传感器的存在和发展赋予了物体视觉、听觉和嗅觉等感官,具有类似人类的大脑和五官的一些功能,在众多方面起着越来越重要的作用。现如今传感器技术已经广泛应用于信息、测量、检测等多个领域。传感器有多种形式,其中力传感器能够使机器人对力具有感知能力,故而力传感器是机器人重要的一类传感器[1]。
六维力传感器是一类非常重要的能够检测空间六维力和六维力矩所有信息的传感器。美国Draper实验室在1975年研究发明了一种六维力传感器,其应用了三层结构的Waston竖梁式,但是存在比较严重的维间耦合[2];A.Gaillt和C.Reboulet在1983年第一次提出了基于Stewart的多维力传感器,此类传感器也存在一定的耦合[3]。
由于六维力传感器测量精度较高并且测力信息较为丰富,因此,随着现代科技的发展,六维力传感器得到了极其广泛的应用。如:双手协调、精密装配、轮廓跟踪;火箭发动机的推力测验[4-5];航空领域中空间站的对接仿真模拟[6]等。随着六维力传感器在多领域方面的应用,为了提高其检测精度和工作效率,需要运用合适的方法对其进行解耦。
1 耦合、解耦的概念
1.1 耦合
耦合是指两种运动形式间或两个或两个以上的体系间通过相互作用而相互影响以致联合起来的现象。在现代化的工业生产中,不断涌现出一些较为复杂的装置或者设备,这些装置或者设备其本身所要求的被控制参数往往是比较多的,故而,必须要设置多个控制回路对该类设备进行控制。因为控制回路的增加,往往会在它们之间造成相互影响的耦合作用,即系统中每一个回路的输入信号对所有回路的输出都会有影响,而每一个回路的输出又会受到所有输入的作用,因此,要想一个输入只去控制一个输出几乎不可能,这就构成了“耦合”系统。维间耦合是影响多维力/力矩传感器测量精度的一个主要因素。
1.2 解耦
解耦就是要在最大程度上减小或消除耦合干扰。六维力/力矩传感器的解耦是通过数学的方法用尽可能小的误差唯一地确定出来传感器的输入与输出的关系。
2 常用六维力传感器解耦方法
一般消除耦合或者抑制耦合可以从两个方向来做:第一种是在生产传感器之前进行的工作,即从传感器的设计上来消除或者抑制耦合,该方法涉及到了传感器的制造工艺问题,这个往往比较困难,并且可能会增加成本;第二种则是利用系统性的数学模型,运用数字信号处理的方法来减少或者消除传感器的维间耦合,该方法对制作工艺要求比较低,比较容易达到,而且还能取得很好的效果。
2.1 六维力传感器静态解耦方法
2.1.1 基于最小二乘法的线性解耦原理
假定六维力/力矩传感器的输入与输出是线性关系,通过运用最小二乘法来确定其相关的参数[7-8]。最小二乘支持向量回归解耦合方法对误差的忍耐度较好并且保持了其广泛化的能力,但是此方法对样本容量有一定的局限性,在样本数量多的情况下它的解耦速度将会受到很大的影响[9]。对六维力/力矩传感器运用最小二乘法静态解耦,可以很直接地在MATLAB中应用最简单的命令来求解且易于理解,思路简单清晰,算法也容易获取,当其需要求解的模型是线性比较好的模型时,应用最小二乘法进行拟合逼近保证了方法和模型的一致性,故而可以使拟合的精度达到很高[10]。但是此方法也有一定的缺陷,当数据样本采集的数量增多时,求解结果的误差中随机误差所占的比例也在随着增大,而最小二乘法对于随机误差的忍耐度较小,因此采集样本的数量增多会对标定矩阵的求解结果造成较大的影响。
2.1.2 基于查询表的六维力传感器解耦方法
将六维力/力矩传感器看作是一个黑箱,通过统计分析实验数据,运用统计学的方法建立黑箱的数学模型来实现传感器的非线性解耦合,此类统计学的方法有支持向量机算法、神经网络算法等。
2.1.3 基于模糊推理的六维力传感器解耦算法
模糊推理需要经过3个步骤:①模糊推理的输入;②建立模糊推理规则;③输出信息的解模糊。其推理过程如图1所示。
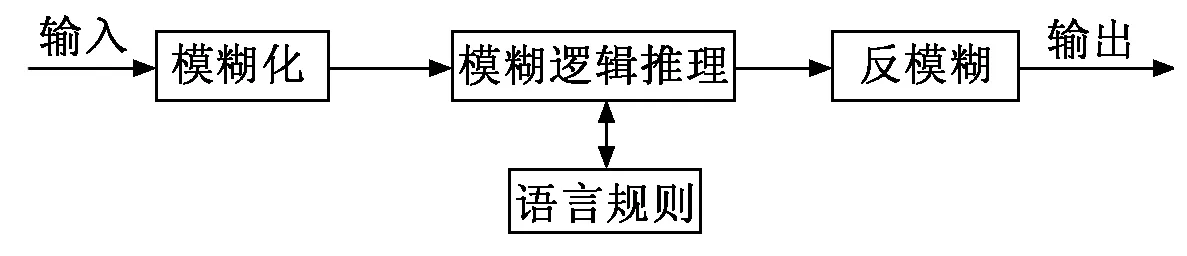
图1 模糊推理框图
2.2 六维力传感器动态解耦方法
六维力传感器被应用在很多场合,要求其能够迅速、精确地反映被测数据的变化等,因此为了实现这些目标需要进行动态解耦。
2.2.1 不变性动态解耦方法
1999年合肥工业大学徐科军等以不变性原理为基础提出了一种传感器的动态解耦方法,通过添加解耦网络来降低解耦模型的阶数,应用低阶的解耦模型消除各个维间的耦合干扰,但是其实现难度较大[11]。
2.2.2 迭代动态解耦方法
迭代解耦的原理是通过对不变性解耦之后的输出结果的迭代来达到理想化的效果。若利用此结果的输出信号来估计另一个通道上的耦合信号,将会得到一个更加精确的输出结果,多次重复这些过程输出结果会更加精确。
2.2.3 对角优势化补偿解耦
2001年东南大学宋国民等提出了一种动态解耦方法——对角优势化补偿,通过设计补偿器来达到近似解耦,并在计算和理论上验证了对角优势补偿之后耦合输出明显减小,但是其没有在理论上完全地展示六维力传感器的动态耦合关系,只能实现近似解耦,并不完全[12]。
3 总结
硬件解耦的方法不仅涉及到很多难以解决的技术工艺问题,而且还会增加制造传感器的成本,与此相比,软件解耦价格低廉、精确度高且可行性强。软件解耦即运用解耦算法通过对应的公式计算以最大程度地减小耦合带来的负面影响,从而提高传感器的精确度,传统的以求解矩阵广义逆为基础的静态解耦算法涉及到很多矩阵运算,其运算量极大,算法复杂,很容易产生病态矩阵,进而影响解耦的精确度。
目前动态解耦以传递函数为基础的有矩阵分析法,其解耦网络简单,思路清晰,但是动态解耦对多维力传感器模型的准确性要求较高,在实际应用中因为系统中干扰和测量误差的存在,并且其辨识方法具有局限性,使其辨识到的系统模型往往不太准确,因此对系统的精确度影响极大。
静态解耦和动态解耦各有优缺点,故而还需要对其进行更深入的研究,比如将新型的动态解耦和静态解耦方法相结合,此技术将会成为未来的研究热点。
参考文献:
[1] 张成艳.基于LabVIEW的新型六维力传感器静态标定实验研究[D].重庆:重庆大学,2012:1-4.
[2] Wastion P C,Drake S H. Method and apparatus for six degree of freedom force sensing :US Patent,4094192[P]. 1978-06-13.
[3] 安巧联.并联结构六维力与力矩传感器的标定原理与关键技术研究[D].秦皇岛:燕山大学,2006:2-3.
[4] Doebelin E O.Measurement system applications and design[M].New York:McGraw Hill,1985.
[5] Diddens D,Reynaerts D,Rrussel H B.Design of a ring-shaped three-axis micro force/torque sensor[J].Sensors and Actuators A,1995,46(1-3):225-231.
[6] Zhang C F.Study on six-degree-of-freedom simulation for docking[J].Space Flight Control,1999(1):70-74.
[7] Berkelman P J,Whitcomb L L,Taylar R H,et al.A miniature microsurgical instrument tip force sensor for enhanced force feedback during robot-assisted manipulation[C]//IEEE Trans Robot Autom.[s.l.]:IEEE,1991:7-21.
[8] Chang Y H,Huang Y C,Liu Y P,et al. A novel structural design for force/torque sensor[J].Meas Sci Technol,1998:196-203.
[9] 龚莉杰.一种新型多维力传感器及其标定方法的研究[D].哈尔滨:哈尔滨工业大学,2015:26-33.
[10] Wang L,Beebe D J.A silicon-based shear force sensor:development and characterization[J].Sensors & Actuators A Physical,2000,84(1):33-44.
[11] 徐科军,殷铭,张颖.腕力传感器的一种动态解耦方法[J].应用科学学报,1999,17(1):39-44.
[12] 宋国民,张为公,翟羽健.基于对角优势化补偿的传感器动态解耦研究[J].仪器仪表学报,2001,22(4):165-167.

