基于机器学习的机器人辅助椎弓根植钉规划

苏全健 孙 宇 齐晓志

1(中国科学院深圳先进技术研究院 深圳 518055)

2(哈尔滨工业大学深圳研究生院 深圳 518055)

1 引 言

椎弓根植钉手术一般用于治疗严重的胸腰椎骨折等造成的脊柱不稳定以及脊髓神经损伤等疾病。由于脊柱病变部位的结构复杂且含有神经组织，手术一旦失败将会造成不可挽回的后果。目前主要通过开放式的椎弓根植钉手术将螺钉拧入椎体，但由于可能存在横突缺失、过大、过小，关节突增生、内聚或者在既往手术过程中已经被咬除等问题，将会导致椎弓根螺钉的入点难以确定，且开放式的手术不利于病人的愈合。据国外文献统计，传统脊柱外科手术导致的各种并发症累积发生率达 52.58%[1]，而仅在胸椎等危险区域的神经硬膜损伤的发生率高达 36.4%[2]。随着社会发展和技术进步，现代手术技术向微创和精准方向发展，急需脊柱手术机器人技术来满足现代脊柱手术精准操作和安全控制的要求。目前本研究团队已成功开发脊柱手术机器人系统，该系统能够辅助医生完成椎弓根植钉手术[3]。本文在微创脊柱手术机器人系统基础上，提出基于机器学习的椎弓根辅助植钉规划方法，在传统的规划方法上进一步优化，大大减少了医生在手术规划上耗费的时间与工作量。

在机器人辅助椎弓根植钉手术中，医生进行椎弓根植钉规划时需要在手术导航软件的图像操作界面反复查看计算机断层扫描(Computed Tomography，CT)图像，通过在脊柱椎体横断面、矢状面、冠状面视图中不断调整椎弓根植钉的位置来完成手术规划。在这个过程中，医生需要花费大量的时间在查找确定适合椎弓根植钉的位置上，这不仅需要医生对导航软件非常熟悉，而且增加了手术时间，使医生的工作量增加，不利于手术的顺利进行。随着机器学习在各个领域的应用发展，将机器学习运用于医疗领域具有很大的发展潜力[4]，通过机器学习可以判断病变部位和病变种类等[5-7]。将机器学习运用于医疗图像中进行相关病症的诊断能够起到很大的帮助，如韩国首尔大学医学系从临床角度批判性地回顾了机器学习分类器在情绪障碍患者的脑部结构磁共振成像当中的应用[8]；美国德州大学达拉斯分校的研究人员研究了机器学习在计算癌症生物学中的应用[9]。目前，国内将机器学习应用于医疗领域已经成为研究热点，如南京大学研究了将机器学习运用于肺癌与正常图像分类[10]；上海交通大学也开展了将机器学习运用于立体脑图像的研究[11]，借助机器学习的方法获取脑部图像的相应特征，从而提出能够提高立体脑部图像配准精度的新型配准框架。过往研究多将机器学习用于对软组织图像的分割，而用于脊柱手术中的研究还未有报道。

针对上述问题，本文提出了一种快速的机器人辅助完成椎弓根植钉规划的方法。首先，采用机器学习的方法对患者 CT 图像中适合做椎弓根植钉手术规划所在位置的图像进行识别，达到快速定位到植钉安全约束区域的目的。然后，在定位到的图像上完成植钉规划，医生只需要在安全约束区域内的规划上完成最终的手术任务规划，能够减少医生花费在手术规划上的时间和工作量。将机器学习应用于椎弓根植钉手术中，能够更加快速地确定手术位置，从而快速地辅助医生完成手术规划，大大减少术前的准备时间，提高手术效率。

2 机器学习模型

2.1 卷积神经网络

目前比较常见的机器学习模型和方法主要有自动编码器[12]、限制波尔兹曼机[13]、深信度网络[14]、卷积神经网络(Convolutionnal Neural Networks，CNN)[15]。其中，CNN 是有监督学习下的机器学习的模型之一，具有非常强的适应性。该算法特别适用于挖掘数据的局部特征，提取全局的训练特征并进行分类，广泛应用于图像的识别和分类，所以本文采用卷积神经网络进行脊柱 CT 图像的识别。CNN 本质上是多层的监督学习神经网络，主要分为输入层、隐含层和输出层。其中，隐含层中的卷积层和池化层是实现卷积神经网络特征提取的核心模块。卷积神经网络的低层由卷积层和池化采样层交替组成，逐层提取特征；高层则由全连接层和逻辑回归分类器组成。第一个全连接层的输入是由低层的卷积层和子采样层对输入图像进行特征提取后得到的特征图像。最后一层的输出层是一个分类器，在分类器之前通常采用逻辑回归，Softmax 回归甚至是支持向量机的激活函数对全连接层提取到的特征进行激活，实现对输入图像进行分类。

2.2 卷积神经网络模型设计

本文使用的卷积神经网络架构如图1所示。整个卷积神经网络共有 8层，主要分为输入层、隐含层和输出层。其中，隐含层主要分为前 5层卷积层和后 3层全连接层。

图1 卷积神经网络架构Fig.1Convolutional neural network architecture

2.2.1 输入层

输入层主要是输入带标签的样本图像，样本图像将会作为整个卷积神经网络的输入以及最后一层全连接层的标签。样本图像通过整个网络的运算在到达最后一层时得到一个特征向量，该特征向量与标签进行对比计算损失函数，进而反向调整各个层的参数。本文输入图像的尺寸为255×255像素。

2.2.2 隐含层

卷积层 1和 2是相似的运算，包含了卷积运算、归一化运算和激励运算。卷积层后接池化层 1和 2，后 3层卷积层是相似的运算，包含卷积运算和激励运算。卷积层和池化层的作用是：一方面，保留不变性，这种不变性包括旋转、平移、尺寸等；另一方面，在保留特征的同时减少参数和计算量，实现降维，防止过拟合，提高泛化能力。多层次的卷积和池化操作能够提高整个卷积神经网络的深度，减少整个网络的参数。同时，不同的卷积层和池化层能够提供不同的感受视野，可以感受不同尺度的特征。多层次的隐含层中的某一个神经元由上一个网络层中的多个神经元乘以权值再加上偏置之后得到，成为权值共享，能够扩大局部视野。权值和偏置在学习过程中通过不断地反向迭代调整能够求得输出函数的最优解，也就是实现最终的损失函数最小化。为了防止网络梯度的下降甚至消失，在通过一定的卷积层后需要进行全连接和回归。隐含层 1对图像的运算流程如图2所示。其他隐含层的图像运算相似，只是卷积核大小不同。

图2 隐含层 1的图像运算Fig.2Image operations of hidden layer 1

隐含层 1中卷积运算使用 3个卷积核，卷积核大小为 11×11像素，卷积步长为 4×4像素。卷积核和卷积步长较大能够使输出特征的尺寸较小，有利于加快第一层卷积运算的速度。卷积与池化操作后输出特征图的大小可以由公式(1)、(2)获得，最终的输出特征图大小为 64×64像素，设定输出的特征图数量为 96。

其中，Nh、Nw为输出数据的长和宽；Ih、Iw为输入数据的长和宽；Ph、Pw为填充的长和宽；Kh、Kw为卷积核的长和宽；Sh、Sw为卷积步长的长和宽。

卷积运算之后需要对数据进行归一化运算，归一化运算的目的是：一方面，避免在卷积神经网络学习的过程中，由于下一步激活运算的输出较大而导致梯度变小的问题。因为在机器学习过程中，梯度越小，学习的速率越慢。如果前面的卷积层不进行归一化运算，那么会造成整个卷积神经网络中，浅层网络基本不学习，而深层次网络一直在学习的情况。另一方面，为了防止训练过程中因为数据分布的不同或者训练数据和测试数据分布不同，而导致模型泛化能力下降的问题。为了适应激活函数，归一化的范围需要相应的调整。因为下文中使用的激活函数是 ReLu，所以归一化的范围是 0～1。归一化过程为，首先通过公式(3)、(4)计算输入特征图的数据均值和方差，然后根据公式(5)对数据进行标准化。

其中，为输入的数据集；为输入数据集的均值；为输入数据集的方差；为归一化后的数据。

为了在正向传播过程中不改变当前的输出，假设训练参数，使得特征图的输出不变，只记录下训练参数，如公式(6)所示。

归一化运算后需要对得到的特征图进行激活运算即做非线性运算，使用激活函数添加非线性单元，可以降低学习过程中的网络过拟合现象。常用的激励函数有 Sigmoid、Tanh(双曲正切函数)、ReLu(Rectified Linear Units)、ELU(指数线性单元)。本文采用 ReLu 函数，如图3所示，通过将数据进行 0～1的归一化处理，避免出现ReLu 函数在 x 值小于 0时梯度为 0的情况。

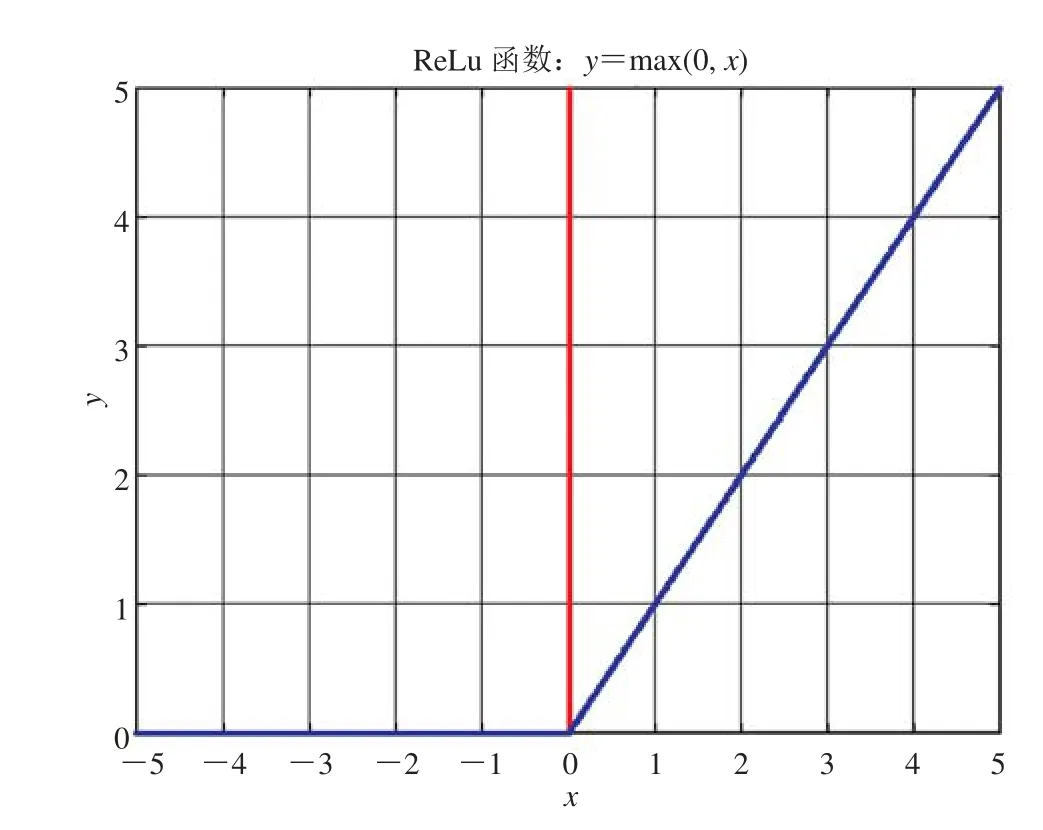
图3 ReLu 激励函数Fig.3ReLu excitation function

2.2.3 输出层

最后一层分类层即输出层，按照训练样本的分类种类将学习网络学习得到的特征转化成特征向量。由于本文将样本种类分为 8类，所以输出层得到的特征向量为 8维，每一维揭示了样本图片属于该类别的概率大小。在输出层之前添加最后一层全连接层并进行 Softmax 激活操作得到最终的特征向量，即全连接层 8通过将前面神经网络学习得到的特征图(文中 4096个特征图)进行卷积操作，得到最后的 8维特征向量。该层的最后是分类函数。其中，分类函数主要用于计算测试精度和损失值来衡量整个卷积神经网络的准确性。输出层的网络示意图如图4所示。

图4 输出层网络示意图Fig.4Output layer network diagram

2.3 损失函数计算及反向传播算法参数调整

2.3.1 损失函数的计算

本文卷积神经网络解决的是 8个类别的分类问题，所以最后的输出层应该有 8个神经元。样本真实类别对应的神经元输出是一个接近于 1的概率值，而非样本真实类别的神经元输出的概率值应该接近于 0，8个类别的概率值的和等于 1。本文卷积神经网络的最后一层全连接层采用的激活函数是 Softmax，定义如公式(7)所示。

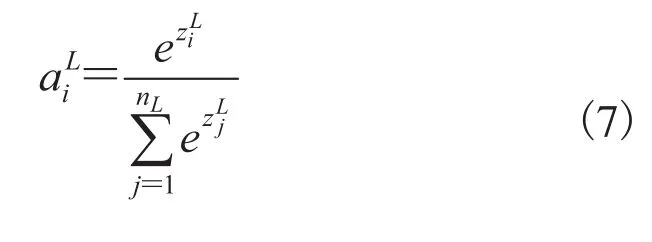
其中，nL为 L 层即输出层神经元的个数；为第i 个神经元的值；为第 i 个神经元激活后的值。

经过激活运算后，保证了输出的值在(0，1)，而作为激活函数的归一化因子，保证了最终所有输出神经元的和为 1。针对Softmax 激活函数，本文选用对数似然函数作为损失函数，定义如公式(8)所示。

其中，W、b 分别为卷积运算中的权值和偏置；yk表示理论输出与实际输出是否一致。假设训练样本的实际输出为第 i 类，则 yk的取值如公式(9)所示。

公式(8)可以转化为公式(10)，其中，i 为训练样本的实际类别。

2.3.2 反向传播算法参数调整

利用反向传播算法来调整权值和偏置是卷积神经网络在学习过程中能够得到最优解的关键步骤。通过前向传播得到的损失函数采用一定的优化方法，反向逐层迭代求取损失函数关于每层的权值和偏置的微分，然后进行更新，经过多次迭代使得最终的损失函数最小化即实现输出函数最优化。由损失函数反向传递时，首先需要求取关于权值 W 和偏置 b 的梯度表达式。W 的梯度计算如公式(11)所示。

其中，因为第 L 层的第 i 个神经元的值为：

所以，最终损失函数关于 W 的梯度为：

同样可以得到关于偏置 b 的梯度计算如公式(14)所示。

根据得到的权值和偏置的梯度，引入学习率，即可在梯度的方向上对权值 W 和偏置 b 进行修正，修正后的表达式如公式(15)、(16)所示。

3 脊柱骨 CT 图像样本分类

3.1 样本分类标准

机器学习分为有监督学习和无监督学习。其中，有监督学习是通过已有的训练样本去训练得到最优模型。本文采用的是有监督学习，所以需要对样本进行分类。对于脊柱骨 CT 图像来说，横断面是非常适合用于判断是否适合椎弓根植钉的断层面，在横断面上可以快速定位椎弓根植钉的安全约束区域，且横断面的特征较为明显，适合用于样本图像的分类。为了使最终分类样本中类与类之间有明显的不同特征以及获得期望得到的分类，采取以下分类标准。

如图5所示，把脊柱部位横断面图像的特征均分为 9个区域，每个区域包含一个特征，样本的分类将会按照是否包含 9个特征或 9个特征中的几个特征组合进行分类。其中，样本特征中的特征 7、特征 8、特征 9是样本分类中的精标准特征。本文把包含精标准特征和其他特征的图像归类到目标图像，不包含全部精标准特征的图像归类到非目标图像。在非目标图像的基础上依据包含不同的其他特征进行细分，有利于提高机器学习的卷积神经网络的学习效率和准确率。如图6所示，依据是否包含特征 1～9，将样本图像分为 8类。

图5 样本特征分布Fig.5Sample feature distribution

图6 各样本图像包含的特征Fig.6Characteristics of each sample image

由于样本图像在获取的过程中会受到 CT 扫描角度、扫描过程中的抖动等因素的影响，建立样本图像的分类标准后，在进行图像的分类前需要对图像进行一定的预处理。为了减少抖动对样本图像造成的噪声影响，需要对图像进行降噪处理。常用的降噪处理方式有均值滤波、中值滤波等。如图7所示，分别为采用均值滤波和中值滤波对有噪声图像进行降噪处理的结果。

图7 不同滤波处理效果图Fig.7Effects of different filters

为了解决由于扫描角度不同而造成样本图像位置偏移的问题，应在网格划分特征区域辨别图像种类时对网格进行平移，以达到正确获取图像特征区域的目的，从而对其进行正确分类。建立网格时，首先通过寻找图像的最大连通区域的圆心，即脊柱骨内脊髓中心所在位置，以该位置为中心建立网格用以划分特征区域。通过上述图像预处理过程，可以得到 8类样本图像，分类结果如图8所示。其中，样本 1为目标图像，其余为非目标样本。

图8 样本分类结果Fig.8Sample classification results

3.2 样本图像训练及结果分析

3.2.1 训练方式

卷积神经网络的训练方式主要有交叉验证法、留出法和自助法。其中，交叉验证法也被称为 K 折交叉验证法，主要原理是将样本数据集分成大小相等的 K 份子集，每一份子集间不存在交集，然后每次训练时取 K－1份子集作为训练集，剩下的一个子集作为测试集。整个样本数据集可以进行 K 次训练和测试，最终的损失值取 K 次训练的平均值。按照经验，K 的取值通常为 10，交叉验证法比较适合样本数据集较小的情况。留出法的原理是直接将数据集分成两个互不相交的子集，其中一个作为训练集，另外一个作为测试集，最终以测试集得到的损失值为测试误差，该方法比较适合样本数据集较大的情况。自助法的原理是假设给定的样本数据集包含 m 个样本，通过有放回的方式随机抽取 m 次得到训练集，没有进入训练集的样本作为测试值。该方法比较适合小数据集，但同时存在一些缺点，如容易引入估计偏差。综上所述，由于本文使用的样本数据集较小，而交叉验证法更适合较小数据集样本的训练。因此，本文采取交叉验证法的训练方式，原理如图9所示。

图9 交叉验证训练原理Fig.9Cross-validation training principle

3.2.2 训练过程

准备好样本训练图像和定义好网络的模型后，接下来就是将样本训练图像作为网络模型的输入不断地训练，以得到最终优化好的输出模型。训练过程中需要对一些参数进行设定，模型训练的参数设置如表 1所示。因为本文采用交叉验证的方式，所以整个样本训练全部完成需要 10次循环。每一次样本全部训练完成记录测试样本集的损失值以及精度，整个模型训练完成的周期为 150，也就是经历了 150次迭代。另外，初始学习率为 0.0001，每经过 15个周期学习率降为原来的 0.2倍。因为模型在训练过程中参数是逐渐最优化的，故学习率较大会导致学习过程中反向传播调节权值和偏置时出现波动，使得模型无法实现最优化。网络采用 GPU 进行训练，最小批量为 128。

图10为网络训练过程中记录的测试集损失值和精度变化情况。由图中曲线的变化过程可以看出，损失函数在训练开始阶段收敛速度很快，在训练中期收敛速度开始变慢并逐渐趋于 0。这与网络模型的优化过程是相吻合的，因为网络模型优化的过程是通过反向传播来调节训练参数使得损失函数最小化。整个网络最终的损失值稳定在0.26左右。测试集的训练精度的变化趋势与损失值是一样的，呈现出逐渐递增并最终趋于稳定在92% 左右。综合网络模型训练过程中的损失值和精度变化来看，模型的优化效果较好，且最终的模型输出能够满足训练的预期。接下来就是将训练好的模型用于验证集的验证，验证集的数据与样本数据集是完全无交集的，能够确保验证过程中不受样本数据的影响。

表1 网络训练参数配置表Table 1Network training parameter configuration

图10 网络训练过程的模型变化Fig.10Model changes in the network training process

3.2.3 模型验证

为了对训练的模型进行验证，取与样本数据集无交集的若干图像组成验证集。在验证数据集中包含样本 1和样本 3图像各 10张，并为其打上标签，用训练好的模型进行分类，将最终的分类结果与标签进行对比，计算最终的预测精度。图11(a)是验证集中标签为样本 1的验证图像，在训练好的模型下的预测结果为：10张验证图像中有 9张预测结果为样本 1，1张验证结果为样本 2，预测成功率为 90%。图11(b)是验证集中标签为样本 3的验证图像，10张验证图像中有 8张预测结果为样本 3，另外 2张的预测结果为样本 5和样本 6。从验证集的预测结果可以得出，本文使用的网络模型能够对图像进行有效的识别，对目标图像即样本 1的识别率较高，通过对样本 1图像的有效识别，能够快速定位到椎弓根植钉的安全约束区域。

图11 网络模型对验证集的预测精度Fig.11 Prediction accuracy of network model to verification set

4 椎弓根植钉辅助规划

4.1 椎弓根植钉的规划方法

脊柱进行椎弓根植钉手术时，对于椎弓根植钉的进钉点、进钉角度来说，螺钉的长度在颈椎、胸椎和腰椎部位是存在一定差别的。对于腰椎段的椎弓根植钉手术，国内外医学界许多有名的研究人员提出了有效的方法，如 Xu 等[16]提出了以两条垂直相交直线的交点为进钉点，垂线为过关节突间隙的延长线，水平线为横突平分线；Kawaguchi 等[17]则提出进钉点位于沿固定椎体上关节突外缘的垂线与横突平分线的交点。国内学者如单云官等[18]提出“十”字定位法，第 1～4节椎体在关节突的乳突后缘中点划垂直线，在横突的副突上划水平线，两线的交点为进钉点；第5节椎体的进钉点是在上关节突的乳突和横突副突之间最深处的中点。上述几种方法均是以横突和关节突为参考，对于第 1～3节椎体，进钉的内倾角范围为 5°～10°；对于第 4～5节椎体，进钉的内倾角范围为 10°～15°。只有进钉的深度保证螺钉的长度达到椎弓根轴线长度的 80%，才能够保证螺钉有足够的力学强度。过长则容易穿透脊柱骨对侧皮质而伤害其他组织，所以长度一般取进钉点至椎体前侧皮质总长度的 83% 左右，螺钉的终止点所在位置与中心线的偏离为椎体宽度的 1/5。图12为腰椎段的植钉示意图，主要从横断面和矢状面去判断椎弓根植钉的规划是否合适。本文将参考上述植钉的角度、进钉的深度和进钉点的选取方法，利用通过机器学习提取到的目标图像进行椎弓根植钉的规划。

图12 脊柱腰椎段植钉示意图Fig.12Implant schematic of lumbar spine

4.2 目标图像植钉规划

通过卷积神经网络提取到目标图像后，为了在图像上自动完成椎弓根植钉的粗规化，需要对目标图像先进行特征提取，如对称中心线，然后根据提取到的特征采用上述植钉方法进行相应的运算操作，完成对钉道的提取。为了对目标图像特征进行有效的提取，需要对图像进行一定的处理，包括图像的二值化、开闭运算以及填充处理。如图13所示，首先，对目标图像的原图进行二值化处理，将感兴趣的特征与背景进行分离；然后，利用图像的开运算去除图像二值化之后背景区域的噪点，利用图像的闭运算对开运算后的图像进行腐蚀操作使图像平滑，加强边缘；最后，利用图像的填充处理操作来填充连通区域内的空洞使图像完整。

图13 目标图像的处理Fig.13Target image processing

利用处理完成的图像提取特征的中心线。中心线的提取需要两个位置的质心：一个是棘突前端质心，通过查找图像当中最小连通域的质心，记为 A 点；另外一个是椎体质心，即图像当中最大连通域的质心，记为 B 点。如图14所示，将A、B 两点连接在一起则为中心线。在中心线上寻找植钉所需入椎体的深度所在位置，通过取过中心线的椎体长度的 80% 所在椎体位置，即图中绿色点所在的位置为中心点，记为 C 点。过该点与中心线垂直的直线为两侧椎弓根螺钉至少应该到达的深度位置所在的直线。

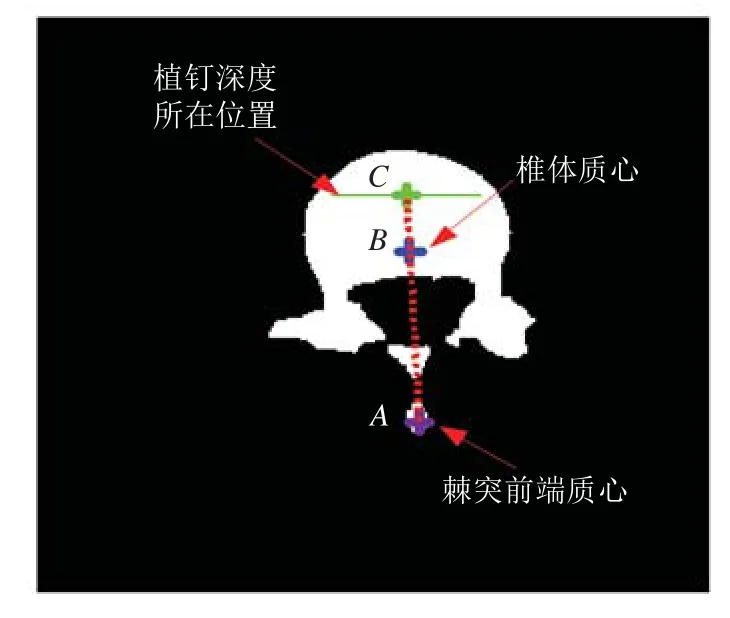
图14 特征中心线提取Fig.14Feature centerline extraction

假设中心线的方程为，则该方程满足通过 A 点和 B 点，即满足公式(17)。

螺钉终止点所在直线与中心线相交且过点C，假设直线方程为，则该方程满足公式(18)。

得到螺钉终止点所在处的直线后，可以求得直线所在处的椎体宽度 L，螺钉植入终止点与 C点的偏移距离为 L/5。设终止点坐标，则通过求解公式(19)中的方程即可得到终止点位置。

通过公式(19)求解得到相对中心线左右两个终止点的坐标，分别记为和。对于腰椎段，螺钉的内倾角是10°～15°，本文统一使用 15°内倾角作为规划的标准。将钉道所在直线延伸至 A 点所在直线处，该直线与中心线垂直。假设为终止点E1的起始点，则满足方程式(20)，求解方程即可得到 S1，同理可得 S2。

图15 钉道规划Fig.15Planning of screw path

则终止点与起始点的连线即为规划的钉道，图15为在二值图像和原始图像中完成的钉道规划。

5 与国内外相似研究的对比分析

本文所提基于机器学习的机器人辅助椎弓根植钉规划方法与国内外现有研究多有不同。如De Bruijne[6]所介绍的机器学习方法主要应用于图像的诊断、疾病的预防和风险评估方面，对机器学习方法在医疗领域中的应用遇到的困难和问题进行了深刻的研究。首要问题是不同成像协议对样本数据的影响，对于脊柱成像方式的不同，提出的解决方案有利于本文网络学习的改进。标签说服力不够是医疗图像识别和分类的一个重要难题，本文的样本图像分类标准很好地对样本图像进行分类，且为样本图像打上了强说服力的标签，解决了这方面的难题。将机器学习作为黑箱子进行诊断和评估是具有风险的。这是因为在高维特征空间的学习系统中，容易受到混杂因素的影响，解决这个问题需要为系统添加补救措施。本文中提出的自动进行规划方法的补救措施是医生的最终规划，为机器学习分类结果的正确性提供了保证。与安杰[19]用机器学习的方法对内侧颞叶癫痫患者全脑白质的研究相比，本文不仅在样本分类上有明确的分类标准，而且根据具体样本优化了网络的架构设计，很好地减少了训练用时，同时提高了图像识别的准确率。

6 结 论

本文采用机器学习的方法对椎弓根植钉安全约束区域的图像进行识别。首先，通过使用卷积神经网络对样本图像进行训练。然后，用训练完成的模型对验证集图像进行了测试验证，得到目标图像后，利用图像的二值化和开闭运算对图像的特征进行了提取。最后，对提取到的特征图像，根据医学上常用的椎弓根植钉的规划方法，利用数学运算求解出钉道的位置并完成了钉道的规划。医生只需要基于安全约束区域内的植钉规划完成最终的手术任务规划，能够减少医生花费在手术规划上的时间和工作量。由于患者个性化差异较大，脊柱各个节段椎体形状千差万别，而本文研究采集的样本实验图像相对较少，未能覆盖全部脊柱节段，造成部分规划钉道出现偏移或较大误差的问题。因此，接下来需要采集更多的样本图像进行训练，同时对本文设计的卷积神经网络进行改进，提高网络的学习效率。

参 考 文 献

[1]Lee MJ,Konodi MA,Cizik AM,et al.Risk factors for medical complication after spine surgery: a multivariate analysis of 1591patients [J].Spine,2013,38(3): 223-231.

[2]姚子明,仉建国,邱贵兴,等.一期后路全脊椎切除治疗重度脊柱畸形围手术期并发症及其相关危险因素分析 [J].中华骨科杂志,2013,33(5):440-446.

[3]Tian W,Han X,Liu B,et al.A robot-assisted surgical system using a force-image control method for pedicle screw insertion [J].PLoS One,2014,9(1): e86346.

[4]Zhang B,He X,Ouyang F,et al.Radiomic machinelearning classifiers for prognostic biomarkers of advanced nasopharyngeal carcinoma [J].Cancer Letters,2017,403: 21-27.

[5]Criminisi A.Machine learning for medical images analysis [J].Medical Image Analysis,2016,33: 91-93.

[6]De Bruijne M.Machine learning approaches in medical image analysis: from detection to diagnosis[J].Medical Image Analysis,2016,33: 94-97.

[7]Suzuki K,Zhou L.Machine learning in medical imaging [J].Pattern Recognition,2017,63: 465-467.

[8]Kim YK,Na KS.Application of machine learning classification for structural brain MRI in mood disorders: critical review from a clinical perspective[J].Progress in Neuro-Psychopharmacology &Biological Psychiatry,2017,80: 71-80.

[9]Vidyasagar M.Machine learning methods in computational cancer biology [J].Annual Reviews in Control,2017,43: 107-117.

[10]史颖欢.医学图像处理中的机器学习方法及其应用研究 [D].南京: 南京大学,2013.

[11]吴国荣.基于机器学习的立体闹图像弹性配准框架研究 [D].上海: 上海交通大学,2007.

[12]Deng L,Seltzer M,Yu D,et al.Binary coding of speech spectrograms using a deep auto-encoder[C]//Conference of the International Speech Communication Association,2010: 1692-1695.

[13]Sutskever I,Hinton G,Taylor G.The recurrent temporal restricted boltzmann machine [C]//Advances in Neural Information Processing Systems,2008: 1601-1608.

[14]Lee H,Grosse R.Convolutional deep belief networks for scalable unsupervised learning of hierarchical representations [C]//Proceedngs of the 26th Annual International Conference on Machine Learning,2009: 609-616.

[15]Krizhevsky A,Sutskever I,Hinton GE.ImageNet classification with deep convolutional neural networks [C]//Proceedings of the 25th International Conference on Neural Information Processing Systems,2012: 1097-1105.

[16]Xu R,Ebraheim NA,Ou Y,et al.Anatomic considerations of pedicle screw placement in the thoracic spine: roy-camille technique versus openlamina technique [J].Spine,1998,23(9): 1065-1068.

[17]Kawaguchi Y,Nakano M,Yasuda T,et al.Development of a new technique for pedicle screw and magerl screw insertion using a 3D image guide[J].Spine,2012,37(23): 1983-1988.

[18]单云官,徐达传,钟世镇,等.骶 1腰 5椎体置入螺钉固定术的应用解剖 [J].中国临床解剖学杂志,1999(2): 63-65.

[19]安杰.应用机器学习方法对内侧颞叶癫痫患者全脑白质的研究 [D].广州: 南方医科大学,2014.