基于Apriori算法的试卷知识点关联分析
□李 毅
一、引言
目前学校教学管理中,对学生试卷分析侧重于借助统计手段得到相关的试卷统计数据,比如,最高得分、最低得分、平均成绩、难度系数等一系列指标,缺乏针对考题知识点的评价,对学生取得这些成绩的知识层面的原因较难深入了解,对教学支持作用存在局限性。多数教师在试卷讲评环节中,对错误率高的题目进行重点讲解,再结合自身经验进行扩展延伸,这会导致试卷讲解过于主观。如何利用成绩数据理性分析学生知识点掌握情况,找出知识点间关联,是广大教师共同关心的问题。
Apriori算法是经典的关联规则挖掘算法之一,能够探究事物间的关联关系,建立关联规则。本文使用Apriori算法,依据学生答题数据,分析出了试卷中各题目对应知识点间的关联性,从而指导教师合理地开展教学。
二、关联规则算法
1.关联规则算法的基本概念
关联规则挖掘方法由R.Agrawal等人在1993年提出,用此算法可对商店顾客的购物数据进行分析,基本思想如下:
设I={i1,i2,…,im} 是二进制集合,其中元素称为项(item),项的集合称为项集(itemset),包含k项的集合为k-项集。记D为交易(transaction)T的集合,这里交易T是项的集合,并且T⊆I。交易的唯一标识记作TID。设X是一个I中项的集合,如果X⊆T,那么称交易T包含X。
关联规则形如X→Y,其中X⊆I,Y⊆I,并且X∩Y=∅。规则X→Y在交易数据库D中的支持度(support)为交易集当中,同时包含X与Y的交易数与全部交易数的比值,记为support(X→Y)。

支持度(support)能够反映X与Y在同一时间内出现的概率。如果二者在同一时间出现概率较小,代表二者关系不大,若二者同一时间出现概率较大,那么说明二者是相关的。
规则X→Y在交易集中的置信度(confidence)为同时包含X和Y的交易数与包含X的交易数比值,记为confidence(X→Y)。

通过置信度(confidence)我们能够判断关联性的强弱,如果置信度较高,那么X与Y的关联性很强。
挖掘特定交易集D的相关规则问题,就是产生那些支持度和置信度分别大于最小支持度和最小置信度的关联规则。
计算频繁项集是关联规则挖掘的关键,主要有两种算法:R.Agrawal提出的Apriori算法,与Jiawei Han 提出的FP-growth 算法。本文采用Apriori算法计算频繁项集,并对知识点的关联性进行分析。
2.Apriori算法步骤
步骤1:确定最小支持度与最小置信度。
步骤2:对事务集D进行扫描,分析事务中出现的项目,如果首次遇到该项目,那么加入候选集C1,并将对应的计数置为1;如果该项数据已加入C1,则将其计数值加上1 得到了候选1-项集。扫描C1,对于计数小于最小支持度的数据项集进行删除,得到频繁项集L1。
步骤3:对Lk-1和Lk-1进行连接生成Lk,得到所有长度为k的候选k-项集Ck。
步骤4:对Ck进行剪枝,删除所有(k-1)-子集不全包含在Lk-1中的Ck中的数据项集。
步骤5:扫描事务集D中的所有事务,如果它包含Ck中的候选数据项集C,则将C的计数加1(初始值为0)。扫描Ck删除那些出现计数小于最小支持度的数据项集,得到频繁项集Lk。
步骤6:重复步骤3 到步骤5,直到Lk为空。
步骤7:对L1到Lk取并集最终即为频繁项集L。
三、Apriori算法在试卷分析中的应用研究
1.数据的准备
本文以某中学初一年级上学期期末数学考试卷面成绩为数据基础,结合学科知识结构及教学主要知识点分布。首先,对试卷各试题所包含的知识点进行统计,如表1所示。然后,对学生题目的作答成绩进行录入,如表2所示。

表1 题目知识点对应关系

续表

表2 学生题目得分表
2.数据的清理
重点检查数据缺失的情况,对于成绩的缺失,通常采用录入平均值的方式。对学生答题情况进行记录,客观题采用“0”和“1”来描述学生试题的正确与否,主观题以得分率进行记录。针对试卷知识点的关联分析中,那些难度过大或过小的题目会导致分析结果对这些题目的关联性过强,影响分析结果。因此需计算各题目的难易度,将过于简单或困难的题目排除。
3.数据离散化处理
由于关联分析只能对处于区间数据进行分析,需要对数据进行离散化处理,处理后,连续的数值会被区域数值代替。得分率小于或等于0.5 的量化为0,得分率大于0.5 的量化为1,如表3所示。

表3 题目分数离散化处理
利用Apriori算法对形如表3所示的数据进行关联规则挖掘。当最小支持度下限设为0.5,最小置信度下限设为0.7 时,产生如表4的部分挖掘结果。
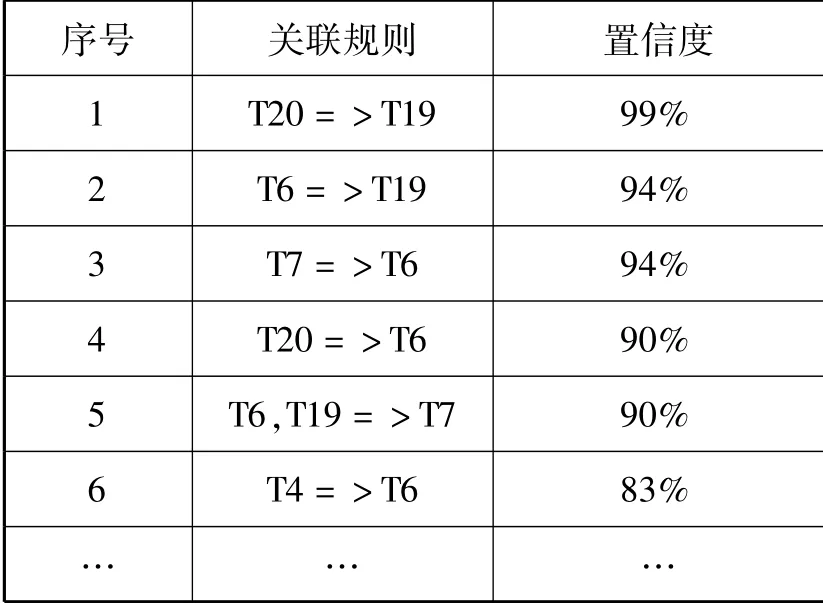
表4 挖掘结果
4.计算结果分析
以下为得到的部分关联规则:
规则1:一元一次方程的应用=>数轴
此规则的意思是:在一元一次方程的应用知识点得分较高的学生对包含数轴知识点的题目得分也会高。这表明考察数轴知识点的题目会结合一元一次方程应用的知识,教师在讲解数轴时,注意带领学生回顾一元一次方程解法的相关内容。
规则2:有理数的混合运算=>频数直方图、用样本估计总体
此规则的意思是:在解有理数混合运算题目得分较高的学生解包含频数直方图和用样本估计总体的题目得分也较高。这说明掌握有理数混合运算是解包含频数直方图和用样本估计总体知识点的基础。
四、小结
通过对试题知识点进行关联分析,能够帮助教师发现一些隐含的知识点间的关联关系。教师可以了解各知识点间的相互影响,为教学提供参考,对日常教学活动进行针对性的调整,提高教学质量和效率。

