基于BP神经网络的网络安全指标体系构建*

刘海天，韩伟红，贾 焰

(1. 国防科技大学 计算机学院，湖南 长沙 410073；2. 广州大学 网络空间先进技术研究院，广东 广州 510006；3. 电子科技大学 广东电子信息工程研究院， 广东 东莞 523808)

0 引言

网络已成为我国重要的信息基础设施，而近年来国内频繁发生的网络安全事件对相关网络软硬件信息基础设施带来了严重威胁。在现有网络安全基础设施及技术基础上，构建大规模网络安全态势分析系统，加强对网络安全态势掌控、分析、预测等处理已经成为了当前的迫切需求。网络安全态势评估(Network Security Situational Assessment，NSSA)技术应运而生，并迅速发展而成为“网络信息安全领域”的一个新的研究热点。

1999 年，Bass等人首次提出了网络态势感知概念[1]，而于2005年，CMU/SEI领导的CERT/NetSA开发了SILK，旨在对大规模网络安全态势感知状况进行实时监控。通过对现有文献的研究，发现要准确预测网络安全态势并非易事，研究人员在这方面做了大量的工作，已经提出了类似“基于威胁传播模型的网络安全评估方法”[2]等有效模型，但并不完美。即便如此，也可以通过前人的经验，结合神经网络与网络安全态势评估技术，以评估结果为指导，提前将影响网络安全的因素进行优化。

相关研究显示，通过BP神经网络模型[3]，可以有效地模拟人类思维模式，进而有效地解决非线性问题。基于BP神经网络的模型构建技术能够很好地应用于网络管理系统中，而采用BP神经网络技术亦可以较好地对网络的安全态势进行评估，而且其在相关研究领域更是具有一定的借鉴价值。因此本文将BP神经网络应用于网络安全态势评估之中，采用大量的实验数据训练模型，并用部分数据进行测试，取得了较好的效果。

1 基于BP神经网络的网络安全指标体系建模

1.1 网络安全指标体系框架

1.1.1网络安全态势综合指数

为了全面反映网络的安全态势，本文采用定量描述的方法对脆弱指数、风险指数和基础运行指数[4]进行计算，这几个指数代表网络安全运行所需要的几个必要条件，而综合安全指数则是指在一定时间段内反映当下网络整体安全态势的数值，它由脆弱指数、风险指数和基础运行指数通过加权法获得，如下图1所示。

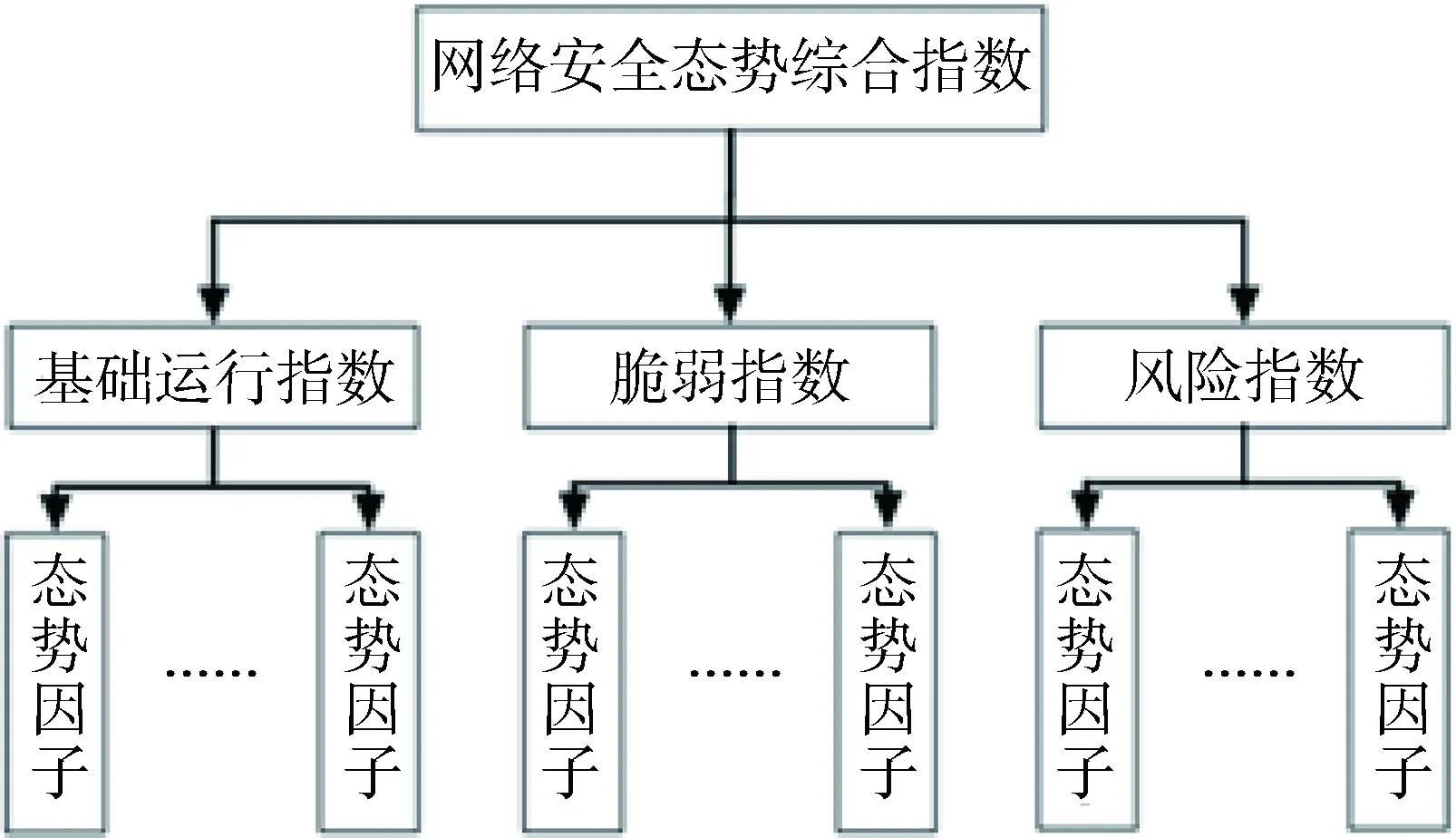
图1 网络安全态势综合指数图

在此，先以基础运行指数作为唯一指标，对基础运行指数进行进一步细化，包括CPU利用率、内存利用率、网络带宽利用率、端口峰值、丢包率、平均往返时延、传输率、吞吐率。选择这8种指标作为评价指，将网络的安全态势进行分级，比如分为5个级别：Good、OK、 Warning、Bad、Critical,这 5 种状态由高到低地标示出整个网络安全状态。

1.1.2BP神经网络模型构建

该模型由态势数据输入、态势映射和态势输出部分组成，各部分的功能设计如下。

(1)态势输入部分：分时段收集网络中节点的态势相关数据，作为态势输入部分的一组输入数据。

(2)态势映射部分：该部分由三层组成，包括输入层、隐层和输出层。

输入层从态势输入部分获取输入数据，这些数据经过隐含层的运算得到隐含层的输出，然后经过输出层的运算得到输出层的输出，态势数据映射完成。

输入层的节点数与输入数据数相同;输出层的节点数与态势评估结果数相同，隐含层数可以根据需要进行设置，但是层数越多、网络越复杂，则训练时间越长。在此，默认初始隐层节点数M为:

M=(N+l)1/2+δ

(1)

其中:N代表输入层节点个数;l代表输出层节点个数;δ代表0～10的常数，默认取值为1。

设输入层有i个节点，隐含层有j个节点，输出层有k个节点;输入层到隐含层之间有连接权值wij，隐含层有阈值θj;隐含层到输出层有连接权值vjk，输出层有阈值rk;第j个隐含层节点的输出值yj，第k个输出层节点的输出值为yk，则:

(2)

(3)

(3)态势输出部分：接收态势映射部分传递过来的值。

BP神经网络态势构建流程[5]，如图2所示。

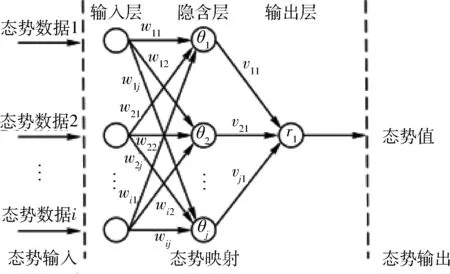
图2 BP神经网络模型态势流图[5]

1.1.3网络安全指标体系模型运行理论基础

评测指标个数与输入层神经元个数一一对应，若有8个评测指标，则网络的输入层有8个神经元，输出要求的评估等级为5，则输出层的神经元为5个，对应的网络输出模式为(1，0,*,*,*)。而经过实验测试，可以进行单一输出元神经输出，隐含层的神经元个数也要确定，默认的取值原则为4个。

最后，经过输入层、隐层得出第一输出层节点(第二隐层节点)。

模拟基础运行维，分别构建脆弱维与风险维的BP神经网络，得到3×n个第二隐层节点，由此完成全局网络的框架。

1.2 指标体系模型运行方式

样本数据m组，解决BP神经网络的训练问题，进行学习训练，使用Eclipse平台构建神经网络作为平台训练BP神经网络，初始化收敛权重并记录，得出理想输出。

各层神经元之间采用全连接方式进行连接，性能目标设为0.1，训练步数设为n次一输出，学习速率设为0.1～0.5，将m组训练数据代入，经过多次迭代运算后达到收敛目标，得出收敛权重。结束训练过程，保存训练好的网络，将5～500组不定测试数据代入网络进行评估。

1.3 基于BP神经网络建模的收敛问题

BP模型在当今的科学技术领域中有着相当广泛的应用，其突出优点是具有很强的非线性映射能力以及根据具体问题灵活处理的柔性的网络结构。但也正是由于BP模型建立了输入与输出之间非线性的函数关系，网络误差和网络参数(权值和阈值)所构成的必定是含有多极点的非线性多维空间。

BP模型采用误差梯度下降法，不论是按标准误差或者是按全局误差，计算流程都是向误差变小的方向进展。由于空间是多极点的，因此计算过程往往滞留在局部极小点而“不能自拔”，又存在着大量的局部极小的“沟谷”，从而影响收敛速度，甚至难于收敛。其次是神经元的传输函数引起的“假饱和现象”等，具体体现为无法收敛(上下波动)和收敛到非目标收敛等现象。

2 模型试验与参数改进

2.1 基于一种梯度下降的反向传播思路的BP神经网络

2.1.1传输函数(激励函数)的选取

在BP神经网络中默认使用logsig激励函数：

f(x)=1.0/(1.0+Math.exp(-x))

(4)

其中，x为所有输入的加权和再减去偏置。

2.1.2误差函数的选取

在BP神经网络中默认使用以下激励函数：

ej(n)=dj(n)-yj(n)

(5)

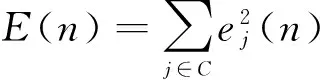
(6)

其中，ej(n)为迭代n时的神经元j输出误差；dj(n)为迭代n时的神经元j的期待响应；yj(n). 为迭代n时神经元j的实际响应；C为所有输出单位的集合；E(n)为迭代n时的瞬间误差平方和(或瞬间误差能量和)，对于n个训练集E(n)的平均值为平均误差能量EA：

(7)

而在此，可以考虑使用另一个误差计算公式更为简单，也更常用：

(8)

2.1.3反向传播流程推导基础

用微分的链式规则，E(n)对wji进行求导：

(9)

其中，wji为神经元i到j的权值；vj(n)为神经元j在迭代n时的函数激活信号，为突触输入的加权和减去偏执。

可得反向传播公式为：

(10)

在一种简单情况下，j为一个输出神经元时：

(11)

其中，φ(x)为激活函数。

然后下面同样分两种情况讨论：

(1)当神经元j为一个输出神经元时：

(12)

(2)当神经元j为一个隐层神经元时：

(13)

(14)

其中，k为j右边的节点。

2.2 基于一种梯度下降的反向传播思路的BP神经网络

2.2.1确定输入和期望输出(随机择取)，反向传播并确定权重，确认收敛性能

实验结论：

(1)当输入输出组数过多时，需要更多的神经元对神经网络的误差进行消减，确保神经网络的收敛性，在小数据范围时，譬如各层神经元比值为输入层神经元数=输出层神经元数=隐层神经元数，拟定10组输入输出，如果不收敛，可以适当增加神经元数，如下图3所示。

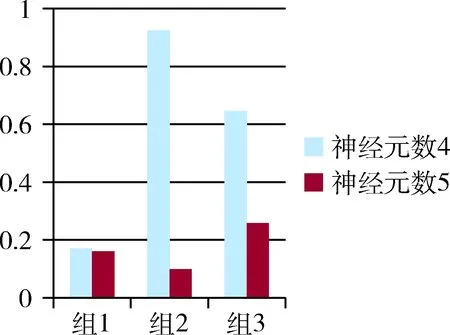
图3 最终稳定误差值图表

(2)数据模型正常运行，在增大输入神经元或者减少输出神经元时可以在一定程度减少最终稳定误差，在进行BP神经网络相关的网络安全指标体系构建时，应尽量确定单一输出，优化并合理提高输入指标数。相关数据如图4所示。本文输入输出推荐使用8:1。

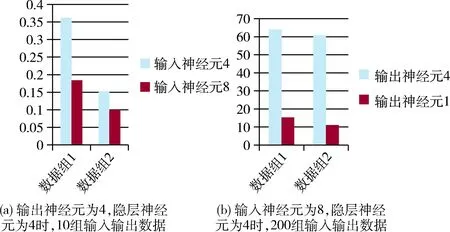
图4 最终稳定误差值图表

2.2.2确定输入和初始权重，得出期望输出，反向传播并重新确定权重，确认单一收敛

实验结论：

(1)当输入输出合理，已确定有合理权重的情况下肯定可以使BP神经网络收敛时，输入输出组数规模较小时，神经元数不会影响神经网络收敛性，但实际权值与理想权值误差则波动极大，如图5所示。

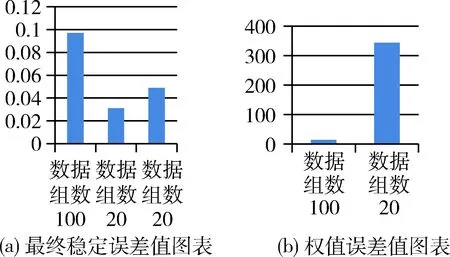
图5 当输入神经元为4，隐层神经元同为4时，最终稳定误差值和权重误差值图表

当网络安全指标体系构建时，应该默认合理权重存在，使BP神经网络完美收敛，而同一个BP神经网络可以通过不同的权重指标进行收敛，在构建网络安全指标体系时，也可以考虑不同的权重指标组可以代表不同的有效网络安全体系指标结构构建。在此，或许可以一定程度考虑忽略神经元数对指标体系构建的影响,关于这一点，可以按实际情况讨论。

(2)在数据模拟进行模糊处理时效果极度不佳，在不进行模糊处理时效果依旧有待改进，在实际考虑中应该优先考虑在P值足够小的情况下便可满足条件，而权重误差值则是另一个靠虑课题，如图6所示。

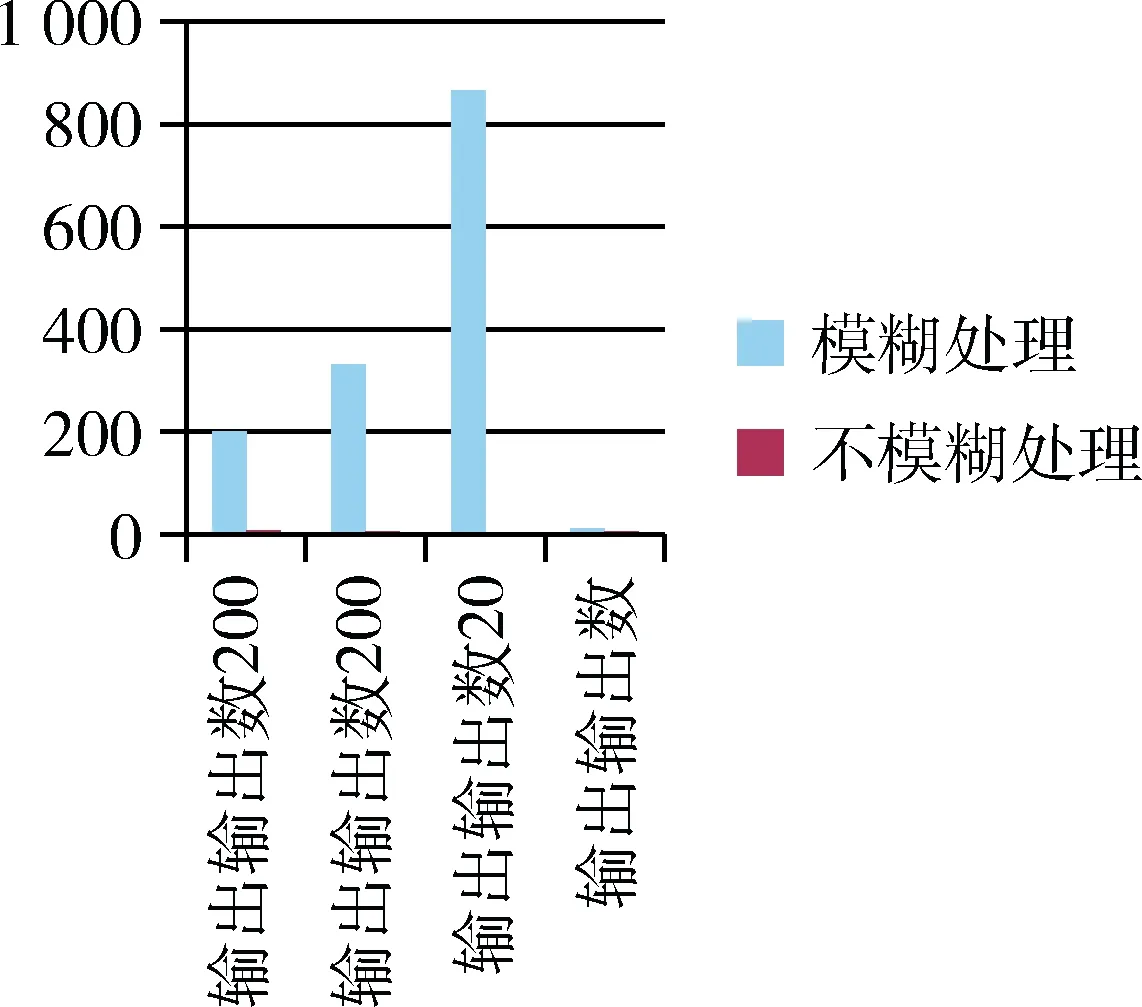
图6 当输入神经元为8：4：1时，对比模糊处理的权重误差值图表

如果考虑收效，不应该墨守成规，可以用实际值进行测试。而在不进行模糊处理时，效果依旧有待改进，则可视之无法收敛到唯一最优解。

2.3 实现指标体系的自我调节与改进

BP神经网络本质上为一个基于梯度的技术，其网络结构的选择尚无统一且完善的理论指导体系，无法访问内在规律，基于简单BP神经网络对网络安全指标体系的构建，根据指标体系构架的收敛问题，在此进行相关的实验与研究，通过一定量的测试，得出对于基于网络安全指标体系构建时的相关参数的优化改良方案，得到了一批可用的基本参数，与改良结果的基础数据结论对比，实现指标体系的自我调节与改进。

经典的BP神经网络优化法有随机优选法、改变误差函数、变步长法、连接权重的选择等[6]，但在实际实验中进行尝试，证明其效果寥寥，较为重点的发现有譬如可以将权重初值限制在[-0.5，0.5]区间内随机选取，可使收敛效果良好等，但结果仍旧不理想。总而言之，本文大体上实现了此次研究的目的与意义，但在此方向上仍需继续努力。

3 结论

关于网络安全指标体系的建模问题，对于基于BP神经网络的收敛问题为该研究的最核心课题，如何将一个基本的BP神经网络契合网络安全指标体系的构建，然后让网络安全指标体系框架进行进化升级，最终得出符合我们要求的神经网络，在这里，提供三个大的方向：

(1)基于普通的梯度下降方法的改进，如随机优选法、动态算法、可变学习速率的自适应调节算法、初始权重选取改进算法等，本文提出的相关算法皆属于第一种；

(2)基于数值计算的改进，如基本的LM算法、牛顿法、最小二乘法等；

(3)混合算法，如BP算法与遗传算法、模糊算法等的结合算法。

参考文献

[1] MURPHY P. The OSPF not-so-stubby area (NSSA) option[M]. RFC Editor, 2003.

[2] 陈锋, 刘德辉, 张怡,等. 基于威胁传播模型的层次化网络安全评估方法[J]. 计算机研究与发展, 2011, 48(6):945-954.

[3] 蒋文科, 吕玉江, 化建宁. 神经网络BP模型的设计与实现[J]. 河北农业大学学报, 2000, 23(1):88-90.

[4] 王志平. 基于指标体系的网络安全态势评估研究[D]. 长沙:国防科技大学, 2010.

[5] 唐金敏. 使用BP神经网络进行网络安全态势评估[J]. 电脑知识与技术, 2011, 7(14):3265-3266.

[6] 高洪深, 陶有德. BP神经网络模型的改进[J]. 系统工程理论与实践, 1996, 16(1):67-71.