CFST柱-钢梁单边螺栓端板连接节点弯矩-转角关系研究

李孝龙高敏

（1.阳光学院土木工程学院 福建福州 350015 2.福建九鼎工程质量检测有限公司 福建福州 350007）

引言

在装配式建筑日益兴盛的今天，在工程中采用CSFT柱-钢梁单边螺栓端板连接接节点能避免现场焊接，具有安装迅速、施工便捷的特点。在力学性能方面，单边螺栓连接的力学性能与传统高强螺栓性能相近，但在闭合截面中施工时却具有普通螺栓所不具有的优势。图1为Hollo-bolt单边螺栓在连接构件时的应用，它能实现闭合截面连接的单侧施工[1]。

图1 Hollo-Bolt安装过程图

弯矩-转角关系是在研究连接力学性能的重要指标。尽管试验和有限元在计算连接弯矩转角关系时都有长处，但是计算时间花费长，转角测量工作量较大，难以在设计时批量的应用。因此为实现快速获得连接弯矩-转角关系，可将试验和有限元分析数据进行拟合，形成简单的表达式。

本文通过有限元分析软件ABAQUS建立了单边螺栓端板连接的三维实体有限元模型，并与已知试验结果进行对比，验证了有限元的正确性。在此基础上讨论了钢材强度、端板厚度、螺栓直径、管壁厚度等因素对节点性能如刚度和极限弯矩的影响，再通过数据拟合出连接-弯矩转角模型中形状系数计算公式，最后将试验和有限元分析结果与理论模型对比来验证该模型的有效性。研究结果可为半刚性单边螺栓端板连接在实际工程中的应用提供技术支持。

1 有限元模型的建立

在建立有限元建模过程中，钢材本构关系采用双折线弹塑性-强化模型，混凝土塑性性能模拟采用塑性损伤模型[2]。

选取实体单元和壳单元对钢管、工字型钢梁、单边螺栓、混凝土和端板进行模拟。选择8节点六面体线性减缩积分实体单元（C3D8R）来对钢管、单边螺栓和混凝土等组件进行模拟。建模过程中，所考虑的接触关系主要包括：混凝土与钢管、端板和钢管、螺栓与端板之间的接触，设置接触时，法向方向选择硬接触，切向方向则采用库伦摩擦模型，摩擦系数值取为0.55。此外，所有接触均定义为有限滑动。模型中除界面接触外，还存在端板和梁之间采用Tie连接，参考点与接触面的采用Coupling连接。为验证所建模型的正确性，分别选取Korol[3]等所做的方钢管柱与钢梁单边螺栓外伸端板连接节点试验中的试件S3、S4与合肥工业大学王静峰[4]在2012年所进行的方CFST柱-钢梁单边螺栓外伸端板连接节点静力试验中的两个试件MES1和MES2进行模拟，模拟结果如图2所示，对比结果表明有限元模型与试验吻合良好，可用作进一步分析的基础。

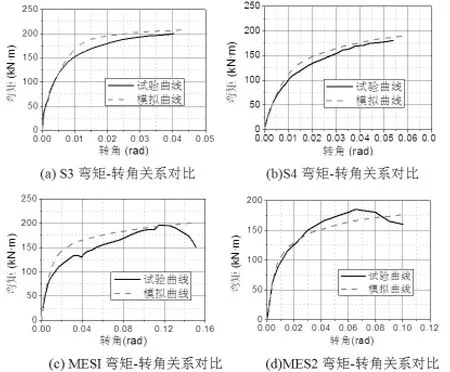
图2 试验与有限元分析结果对比图

2 构件设计

为了能够获取各参数变化对节点初始转动刚度与弯矩的影响，进而为获得形状参数提供参考。建立了15个有限元模型，试件尺寸如表1所示。

各试件中分别考虑了钢材屈服强度、混凝土强度、螺栓直径、端板厚度、端板宽度、柱长细比、柱线刚比等8个参数的影响。基本试件的柱截面尺寸为□300×300×10mm，柱高3000mm，梁截面尺寸为400×200×8×13mm；外伸端板尺寸为 220×680×20mm；混凝土强度 fcu=50N/mm2；单边螺栓屈服强度1048N/mm2；极限强度为1182N/mm2；直径为10.9级M20的HSBB；钢材屈服强度fy=345N/mm2，当研究某一个参数的影响时，保持其他参数不变，只改变该参数。

3 三参数模型的确定

为了便于工程实际应用，需要一套简单实用、准确度高的理论计算模型来描述节点的M-θ关系，Kishi和Chen提出了三参数幂函数模型，该模型曾被用来描述双腹板角钢的顶底角钢连接的M-θ关系，且效果较好，该模型的表达式为：

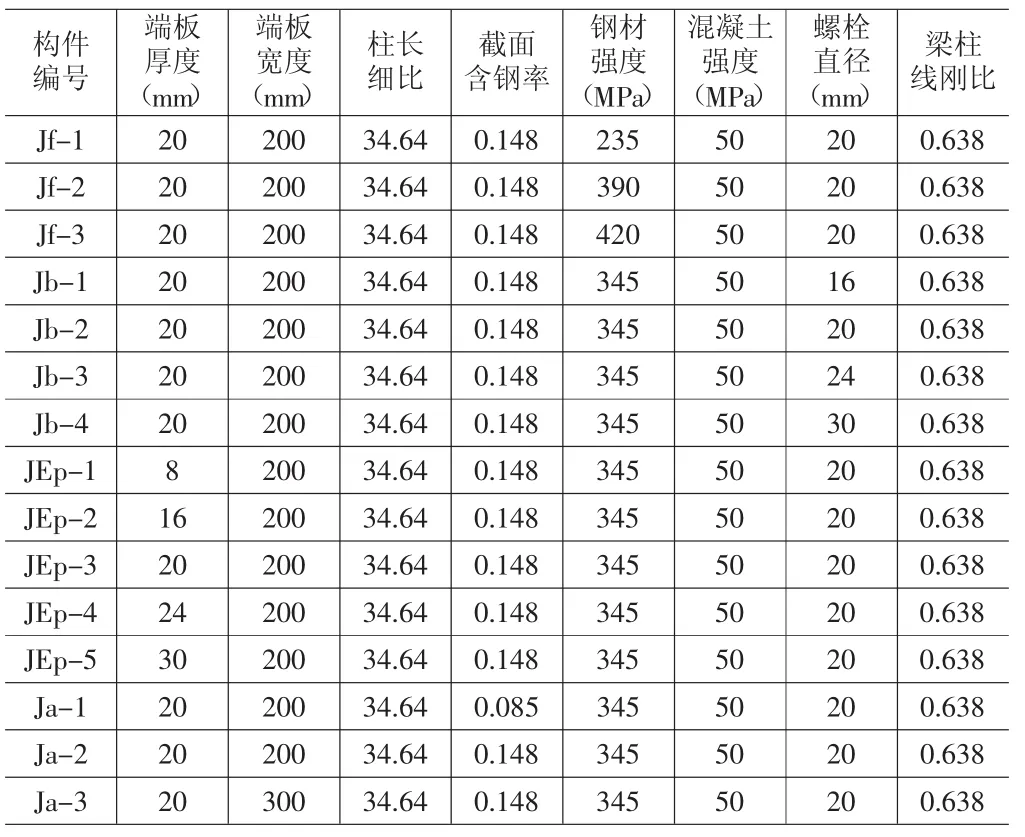
表1 各试件参数

式中，Ki为连接初始转动刚度，Mu为连接的极限弯矩，m为曲线的形状参数，θ0=Mu/Ki，该模型不仅形式简洁，物理意义明确，应用方便。

3.1 各构件刚度计算与曲线拟合

上述弯矩-转角关系理论表达式需三个参数，其中两个参数弯矩与刚度可通过计算表1中的有限元分析得到，再利用式（2）进行拟合，最后对形状参数m进行调整，使公式与有限元分析结果最接近.选择优化的目标函数是：

式中，N为数据点数；Mi为第i个数据点的弯矩值；mi为经公式计算获得的连接处弯矩。对曲线拟合时采用最小二乘法，使W数值最小。有限元计算的弯矩、刚度及拟合各试件的形状参数m汇总于表2，该表中考虑的因素基于各变化参数对节点弯矩与刚度等的影响，故对m的影响也主要包括钢材强度、端板厚度、螺栓直径、管壁厚度等4个参数。

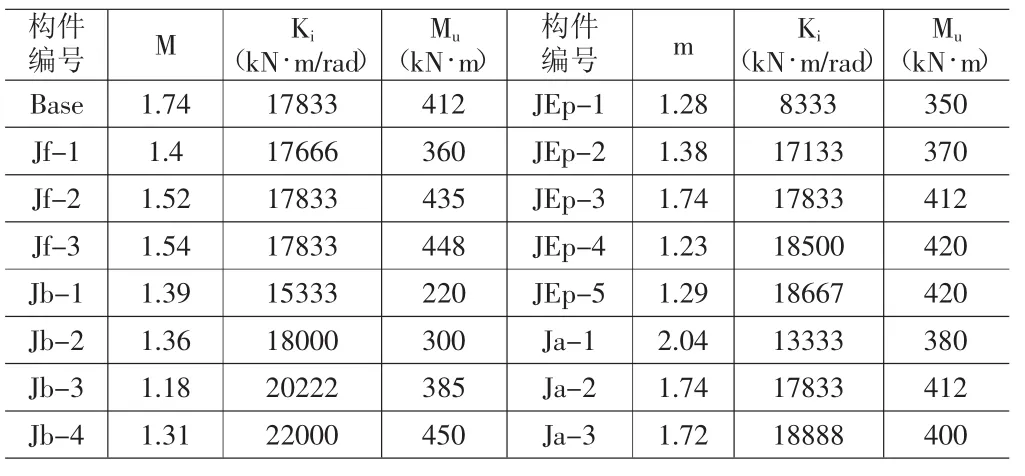
表2 曲线拟合得到的参数值（m）

3.2 表达式参数m回归分析

形状参数m的表达式与连接几何和材料特性有关，故对上述拟合结果进行回归分析。该参数的一般形式为：

式中，a为未知系数，αi是第i个独立变量；xi是回归分析中有待确定的指数；n是独立变量的个数。通过分析选择了其中4个参数用于回归分析，分别为端板的厚度tep、螺栓直径d、钢材的屈服强度fy、柱翼缘厚度tcf。三参数模型中的M-θ关系中形状参数表达式m经matlab回归分析可表示为：

为了评估该参数表达式的可靠性，计算出了其相应的统计结果，其中标准差S为0.02，相关系数R2的值接近为1，表明回归公式与原数据的相关性较好。

4 结论

利用有限元分析模型对CSFT柱-钢梁单边螺栓连接进行了抗弯性能分析，在有限元分析的基础上对连接弯矩-转角关系曲线进行拟合，并对拟合的结果进行了回归分析，得到了便于预测连接弯矩-转角关系计算公式，主要结论如下：

（1）采用非线性有限元分析模型得到的计算结果与试验吻合良好，可用于CSFT柱-钢梁单边螺栓外伸端板连接进行了抗弯性能分析；

（2）外伸端板连接弯矩-转角关系可采用三参数指数模型表达，关键的形状参数可直接用本文的回归公式计算；

（3）回归公式计算得到的形状参数可用在三参数模型中用于计算弯矩-转角关系，通过与有限元与试验结果对比，吻合良好，表明三参数模型能很好地用来计算此类节点的弯矩-转角关系，便于工程设计时使用。

[1]徐 婷，王 伟，陈以一.国外单边螺栓研究现状[J].钢结构，2015，30（8）：27～33.

[2]韩林海.钢管混凝土结构-理论与实践[M].北京:科学出版社，2007.

[3]R.M.Korol,A.Ghobarah，S.Mourad.Blind bolting W-Shape beams to HSScolumns[J].Journal Structural Engineering1993，119[12]：3463～3481..

[4]Jingfeng Wang，B.F.Spencer Jr.Experimental and analytical behavior of blind bolted moment connections[J].Journal of Constructional Steel Research，2013，82（3）：33～47.