“二元一次方程(组)”常见错误分析
◎顾长亮

学习二元一次方程(组)后,在解答一些问题时,部分同学由于对相关定义、解法理解不透,对问题考虑不周,再加上受思维定势等因素的影响,常会犯一些错误.这里举一些常见的错误,供同学们借鉴.
一、方程(组)概念不清
例1下列方程哪些是二元一次方程:
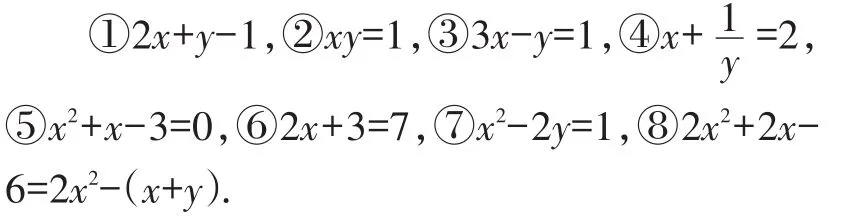
【错解】①②③④.
【学生自我分析】多选了①是因为粗心,没注意代数式缺少等于0;多选了②④,是因为乍一看x和y的指数,以为是一次的;少选了⑧是没注意到等式左右两边2x2可以抵消.
【教师点评】犯错的原因还是概念不清,判断一个方程是否二元一次方程应注意:(1)方程两边的代数式是整式,④不符合这一条,而①干脆连方程都不是;(2)方程中含有两个未知数,与“二元”对应,⑤⑥都不符合这一条;(3)方程中含有未知数的项的次数都是一次,与“一次”对应,②⑤⑦都不符合这一条.所以本题的正确答案为:③⑧.
例2下列哪些方程组是二元一次方程组:
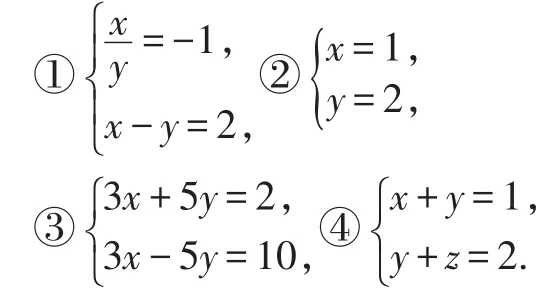
【错解】①③④.
【学生自我分析】以为二元一次方程组是由两个方程组成的,且每一个方程都含有两个未知数.
【教师点评】二元一次方程组的定义∶含有两个未知数的两个一次方程所组成的方程组叫做二元一次方程组.这应从三个方面来理解:(1)两个整式方程的最高次数是1,所以①不符合;(2)方程组中共有2个未知数,所以④不符合.只有②③符合这些条件,它们是二元一次方程组.所以本题正确答案为:②③.
二、方程(组)解的概念不清
例3把二元一次方程-2x-y=-8写成用含y的代数式表示x的形式,并求方程的正整数解.
【错解】因为-2x-y=-8,所以,将y=4代入上式得x=2,所以正整数解为
【学生自我分析】以为二元一次方程的解是唯一的,发现把y=4代进去,x刚好为整数,这样,就是它的解了.
【教师点评】二元一次方程的解一般有无数组,本题加了正整数解的限制条件后,个数不一定是无数个,但也不是只有一个.本题在得出后,由x>0得,即0<y<8.当y为偶数时,x也为整数,又因为是正整数解,所以y只能取2,4,6,所以方程组的解为
三、方程(组)解法不熟练
例4用代入法解方程
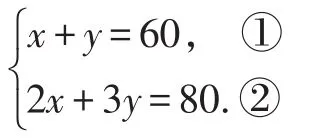
【错解】由①得x=60-y,代入②得2(60-y)+3y=80③,解之得y=40,将y=40代入①得x=20,所以原方程组的解为
【学生自我分析】解方程③的时候解错了,把负号给弄丢了.应该是y=-40,最后正确的解为
【教师点评】代入消元法是解二元一次方程组的一种基本方法,它的一般步骤是:(1)从方程组中选取一个系数比较简单的方程,把其中的某一个未知数用含另一个未知数的代数式表示出来;(2)把(1)中所得的方程代入另一个方程,消去一个未知数;(3)解所得到的一元一次方程,求得一个未知数的值;(4)把所求得的一个未知数的值代入(1)中的表达式,求出另一个未知数的值,从而确定方程组的解.
需要特别提出的是:当方程组中有一个方程的一个未知数的系数是1或-1时,用代入法较简便.该同学代入过程是正确的,在计算中把符号弄错了,另外还需要养成检验的习惯.
例5解二元一次方程组
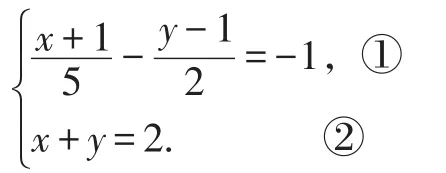
【错解】①×10得2(x+1)-5(y-1)=-1,化简得2x-5y=-8③,由②得2x+2y=4④,
④-③得,,代入②得,方程组的解为
【学生自我分析】应该是①两边各项都要同时乘10,而上述解法只将左边乘10,右边忘记乘了.应由①×10得2(x+1)-5(y-1)=-10,化简得2x-5y=-17③,由②得2x+2y=4④,④-③得,7y=21,y=3,代入②得x=-1,所以方程组的解为
【教师点评】本题是较为复杂的加减消元法解二元一次方程组,方程①中有分母,去分母时,依据等式的基本性质:等式两边同乘(或除以)同一个不为零的数或整式,等式仍然成立.该同学只乘了左边而没有乘右边,导致了错误,这是比较典型的错误,同学们要尽量避免.

