基于波动方程有限差分数值模拟及FCT消频散分析

赵 威，李伟波，桂志先，周 游，于晓东

(长江大学 油气资源与勘探技术教育部重点实验室，湖北 武汉 430100)

0 前 言

地震波正演模拟技术一直被人们视为一种比较直观、形象地了解和认识波在地下介质中传播特性的重要手段。所谓正演模拟，就是在首先假定地下介质模型和相应的物理参数已知的情况下，模拟地震波在地下各种介质中的传播规律，从而根据其计算出的地面或地下各观测点所应观测到的数值地震记录来进行分析地下模型的一种地震模拟方法。地震数值模拟由来已久、发展迅速，目前已经有多种地震数值模拟方法在地震勘探和地震学中得到广泛而有效的应用。这些地震波场数值模拟方法主要可以归纳为3大类，即几何射线法、积分方程法和波动方程法[1]。

波动方程法数值模拟本质上是求解地震波动方程，模拟的地震记录包含了地震波传播的所有信息，能够很好的了解地下情况，从而被广泛应用。波动方程的求解方法有解析法和数值法两种，而波动方程的解很难以用解析形式表达出来，因此，数值法成为求解波动方程的主要方法。波动方程数值模拟的方法主要有有限差分法、有限元法和伪谱法等。相比其他两种方法，有限差分作为一种最常用的数值模拟方法，能够较准确的描述地下介质分布状况及地震波在各种介质中的传播规律。具有计算效率高，占用内存小等特点，但由于其本身时间和空间都采用差分离散形式，往往会出现数值频散问题[2]。怎样减少频散，提高模拟精度始终是有限差分数值模拟的关键问题。为此，学者们做了大量工作，当信号在一个波长范围内，具有多个离散节点是，频散现象基本消失。一般随着网格间距增大，频散问题越严重；反之若减小网格间距相应会增加网格点数，将会大大增加计算量，造成计算时间过长。既能控制模拟精度，又能节省计算时间的方法显得尤为重要。Boris和Book等人首先提出了通量校正传输的方法，它最早起源于求解流体力学连续方程中，随后才开始被运用于声波方程数值模拟的求解；国内杨顶辉等[3]将其应用于弹性波动方程正演数值模拟频散处理，取得一定效果。为了更好的对比分析未加FCT数值模拟和加了FCT 方法的区别，本文基于声波和弹性波两方面，借助于交错网格的模拟优势，对各向同性介质波场进行了有限差分数值模拟，并对其相应的波场快照和计算效率进行对比分析。

1 波动方程有限差分算法原理

1.1 声波方程形式

二维二阶标量声波方程的一般形式为：

(1)

经过化简变形可得到一阶压力—速度方程组形式：

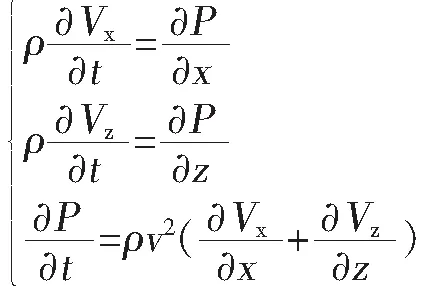
(2)

针对(1)式左右两边使用二阶中心差商公式可得到相应的差分形式：

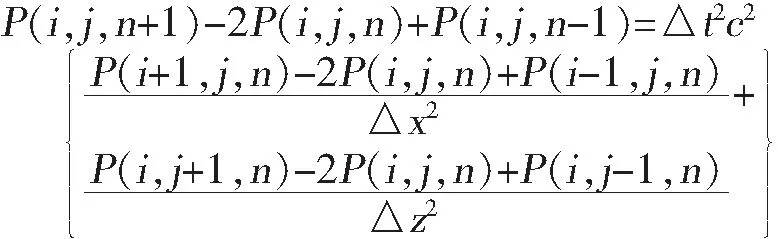
(3)

其相应的一阶压力—速度方程差分形式为：

Δx=Δz=h

(4)

1.2 一阶速度—应力弹性波方程

在二维各向同性介质中，不考虑体力的影响下，弹性波方程可以化为一阶速度—应力的形式：

(5)

方程组(5)中，Vx、Vz表示x、z方向速度分量，ρ表示介质的密度，σxx、σxz、σzz分别表示应力分量，C11、C13、C14为介质的弹性参数。

为了研究方便，我们采用时间二阶、空间四阶交错网格有限差分形式[4]，交错网格的网格化和常规有所区别，交错网格引进了半网格，速度和应力分别在整网格和半网格上计算，

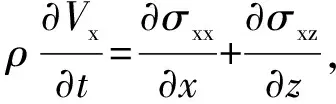
时间的2M阶差分近似：

(6)

上面两式相减，得2M阶精度的差分近似式：

(7)

当M取1时，上式即为时间二阶精度差分格式，带入示例并整理得(8)：

(8)

空间差分格式近似：

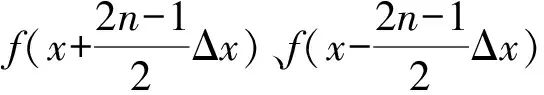
把时间二阶差分精度公式和空间四阶公式代入方程组(5)，可得一阶速度—应力弹性波方程

离散格式：

(10)

2 通量校正FCT方法

通量校正传输法(FCT)最初被广泛应用于流体力学中冲击波前阵面极大浓度梯度过程中，满足连续守恒方程式，守恒定律保证了其方程式和物理定律的一致性。此后，随着应用的推广被引用于声波方程中，在地震波在模型中的传播方程中有效的压制了在构造交错网格差分格式时计算产生的数值频散，即网格交界面边界在同一时刻有流入和流出等量的物理通量，用这种方法可以有效的避免了截断误差的累积。FCT方法主要包含两个步骤即：交错网格有限差分计算和通量的校正[5]。在其通量校正的阶段，用改变波场的方法来压制伪波动。但由于在实际操作过程中并没有事先证明散射存在的位置，所以FCT首先假设所有极值均由数值频散引起，从而对全部的网点进行通量校正，在校正的过程中同时对反漫射进行修正，进而使其结果更加准确。以速度分量vx为例，其具体步骤如下。

1)建立各项同性介质条件下各项同性非均匀介质弹性波动方程，进而得到一阶速度—应力交错网格有限差分方程。由FCT算法的特性可知，在对速度分量vx、vz进行计算后，只要速度分量被校正，其应力分量也会被随之校正。

2)k-1时刻漫射通量的计算：

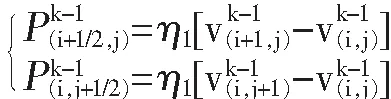
(11)

其中，η1取值范围为0～1，为漫射因子，其值可以是一个常数，根据实际情况可以由数值实验得到。

3)k+1时刻漫射通量的计算。

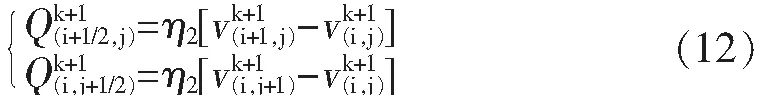
其中，η2取值范围与η1一致，为反漫射因子，通常由于反漫射运算需要补偿人为加入漫射引起的误差和有限差分运算带来的振幅损失，所以一般取值略大于漫射因子η1。

4)对k-1时刻漫射用通量P对速度分量进行平滑修正。

(13)

5)求解k+1时刻的反漫射通量。

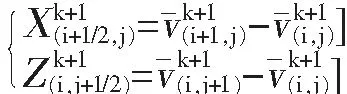
(14)

6)利用反漫射通量进行修正，得到校正之后的速度分量：

(15)

其中：

(16)

3 数值模拟频散分析

有限差分数值模拟是将微分方程离散为差分方程进行求解的过程。当空间网格间距或者时间网格大小选取不合适就会引起波形畸变，地震波在传播过程中，波前形状就会发生变化，并且逐渐散开，这就是所谓的数值频散现象。其本质是离散化波动方程产生的伪波动，这是有限差分方法所固有的本质特征[6]。目前压制有限差分数值频散的思路主要三个方面：一是通过控制网格步长，减少网格步长可以明显提高数值频散，但网格点数会增加，计算量会显著增加；二是提高差分阶数，但差分阶数达到一定时，再提高效果不明显且计算量很大；最后就是利用通量校正传输技术等。

3.1 均匀介质模型

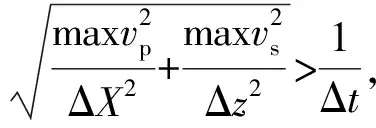
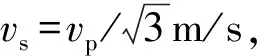
图1为均匀介质声波方程有限差分数值模拟的波场快照。所选网格步长如图1a，从波场快照来看，很明显出现了数值频散，会影响模拟精度；图1b～d是通过减少、缩减网格步长后的波场快照，b图可以看出消频效果明显，但随着不断缩减后期效果并不显著。图1e为FCT消频散后的波场模拟快照，可以看出FCT消频散虽然所用时间较长，但模拟效果较好；与此同时，比较图1d、e达到相同的精度时，通量校正传输的方法所需时间还是相较前者要少，波场清晰度更高，能够起到一定的效果。

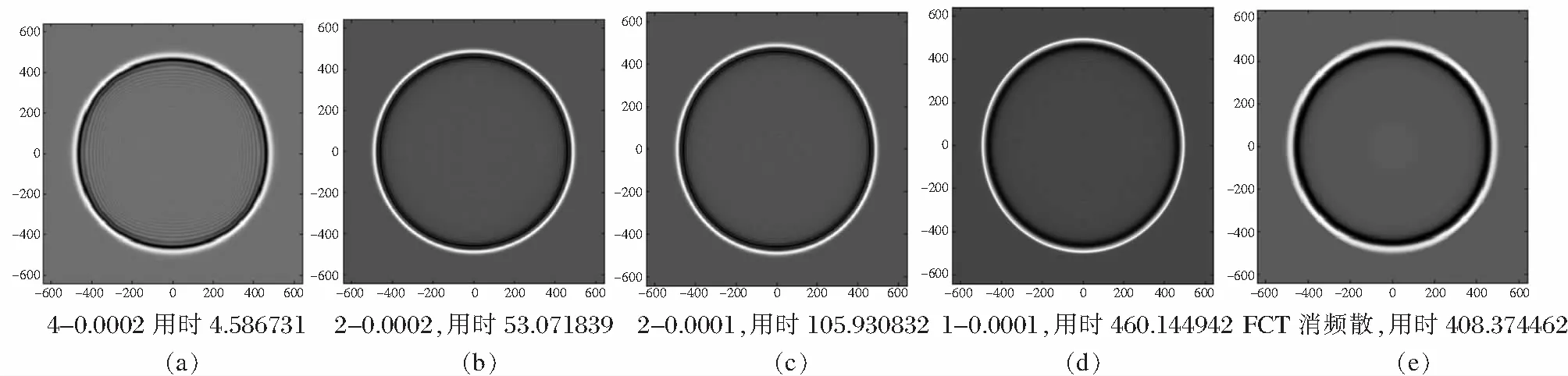
图1 标量声波方程有限差分模拟波场快照

3.2 层状介质模型

图2、3分别为均匀介质模型和层状介质模型的时间二阶、空间四阶交错网格有限差分数值模拟波场快照，通过对比通量校正前后的波场快照，可以明显得到：传统交错网格有限差分在空间步长较大的情况下，波的模拟过程中出现了出现了伪波动，产生了数值频散现象，如图2a、3a；而结合FCT通量校正后的波场快照可以看出(如图2b、3b)，波的扰动明显减少，波场更加稳定平滑，很好的消除频散；再者，传统方法要达到相同精度的波场快照所需时间远远超过FCT。总之，FCT消频散能够明显改善数值模拟结果，能够有很好的压制频散的效果。

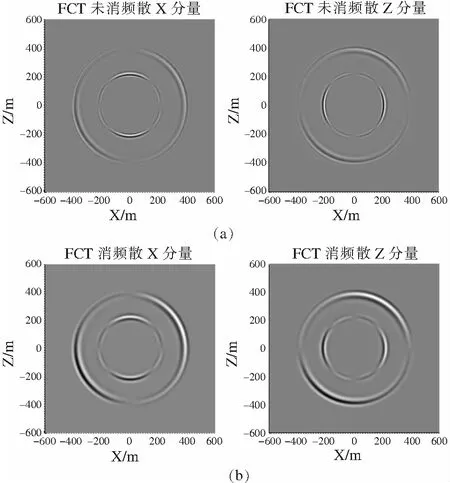
(a)未消频散X、Z分量波场快照；(b)消频散后X、Z分量波场快照(均匀介质模型下)

图2时间二阶、空间四阶交错网格有限差分数值模拟波场快照

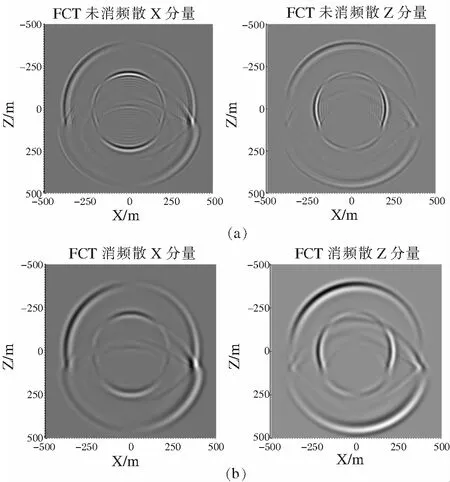
(a)未消频散X、Z分量波场快照；(b)消频散后X、Z分量波场快照(层状介质模型下)

图3时间二阶、空间四阶交错网格有限差分数值模拟波场快照

4 结 论

本文在前人已有的成果基础上，推导了二维声波方程、时间二阶空间四阶弹性波有限差分计算公式，并结合通量校正输出技术(FCT)，给出了具体的实施方法步骤；将FCT运用到基于各向同性介质、层状介质的波动方程数值模拟中。通过对比数值模拟波场快照，可以看出该方法可以有效压制各向同性介质有限差分正演模拟过程中因网格剖分而引起的数值频散。虽然加入通量校正传输技术会需要增加计算量，但相比减小步长，增加网格点数来消除数值频散，对于相同模拟精度下，该方法能够大大减少计算量；与此同时，提高精度的同时，对于较大采样间隔的网格划分能节省计算量，提高相应计算速度。因此可以总结为，FCT是在同性介质下，地震波数值模拟时压制频散问题的一种有效可能的方法。

参考文献：

[1] 李信富，李小凡，张美根.地震波数值模拟方法研究综述[J].防灾减灾工程学报，2007，27(2)：241-245.

[2] 李宾.横向各向同性介质有限差分法波场模拟方法研究[D].青岛：中国石油大学，2009.

[3] 杨顶辉，滕吉文.各向异性介质中三分量地震记录的FCT有限差分模拟[J].石油地球物理勘探，1997,32(2):181.

[4] 岳晓鹏，白超英，岳崇旺.高阶交错网格有限差分弹性波场模拟的精度分析[J].煤田地质与勘探，2017,45(1):125-130.

[5] 李立平，何兵寿.TTI介质弹性波FCT有限差分数值模拟[J].地球物理学进展，2017,3(4):1584-1590.

[6] 吴国忱，王华忠.波场模拟中的数值频散分析与校正策略[J].地球物理学进展，2005，20(1)：58-65.