基于波场重建的时域全波形反演

李松龄

(东北石油大学 地球科学学院，黑龙江 大庆 163318)

0 前 言

勘探地球物理主要的目的是获得对地球内部的精确成像。近年来，随着计算硬件性能的提升以及GPU(Graphic Processing Unit)等高性能计算设备在地震数据成像中的成功应用，具有高分辨能力的全波形反演(Full Waveform Inversion，FWI)方法受到了地球物理学家们青睐[1-2]。对于照明均匀和低频可用的观测数据，理论上，FWI能够同时恢复地下构造的长波长和短波长信息，相当于同时对地震数据做层析和偏移处理[3-4]。因此，具有高分辨率的全波形反演方法在油气勘探开发和地球动力学研究等领域中彰显了更大的研究潜力和发展前景。

时间域的FWI方法最先由Tarantola实现，随后，Pratt将FWI发展到频率域[5]，并发展了由低频到高频的反演策略，Bunk在时域发展了由低频到高频多尺度反演策略[6]。时域和频率域的FWI均有各自的优势，全频带的频率FWI等同于时域FWI。频率FWI在二维情况下优势巨大，在频率域仅执行一次LU分解，便可实现多炮的正演，但对于三维情况下，频率域正演求解变得非常困难。所以，目前多数三维FWI方法的实现常常在时间域完成。

除了初始模型的问题会干扰FWI的应用效果，巨大的计算量和存储量同样也成为影响FWI实用化推广的棘手问题。在FWI迭代计算过程中，反演梯度的计算与逆时偏移(Reverse Time Migration，RTM)方法流程类似，因此，采用互相关成像方法时，震源波场的存储量决定着RTM和FWI方法对计算硬件存储性能的要求。同理，针对RTM方法的存储策略同样可借鉴应用至FWI方法中。Clapp提出在速度外围构建随机速度层作为边界条件[7]，将边界波场能量以随机噪声的形式保存于波场内部，进而通过波动方程的反向计算即可获得历史波场，该方法由于波场存储量较低，被广泛应用于RTM方法中；Shen等对上述方法进行了改进，加强了随机边界对低频数据的散射强度，并应用于波形反演算法中[8]。但随机边界条件产生的随机噪声会对RTM及FWI结果产生干扰，影响最终的成像精度。Clapp提出了一种保存边界波场的存储策略[9]，能够一定程度上的降低波场存储量，而且可应用于吸收边界条件下的波场重建；随后，该方法被众多学者加以改进并应用至RTM计算和GPU加速策略中[10-11]。FENG和WANG等提出了差分阶数的渐变策略[12]，用于进行波场重建，但该方法重建的波场存有一定误差，虽适用于RTM成像，但不适用于基于迭代计算的FWI方法。Kalita和Alkhalifah提出利用激发振幅成像方法实现FWI算法中成像梯度的计算[13]，能够大幅降低波场数据的存储量和计算量，但对于复杂构造，激发振幅成像方法往往在多波至路径的区域会产生走时计算误差，影响成像精度。地球物理学家们目前仍在积极探索针对FWI方法中波场存储量的改进方法，该方面的研究探讨对提升FWI的理论水平和应用价值十分重要。

在前人研究工作的基础上，本文提出了一种基于波场重建的时域FWI方法。借助拉格朗日乘子法，首先推导了FWI的梯度表达式，并引入解析步长方法和混合共轭梯度优化方法求解该反问题。针对FWI成像梯度计算所需的巨大存储量问题，我们引入了一种能大幅降低存储成本的波场重建策略，为时域FWI的实用化推广提供一套切实可行的理论方案。最后通过匀速模型和Marmousi2模型的波场重建和FWI测试验证了本文方法的有效性。

1 方法原理

1.1 全波形反演的梯度

时空域二阶声波常密度波动方程为：

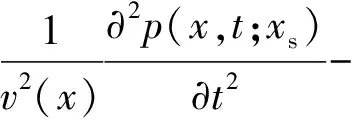
(1)

式中，x是空间坐标；xs为炮点空间坐标；v是地震波传播速度；p是地震压力波场；fs是震源项。定义在检波点处的模拟的数据满足：

pcal(xr,t;xs)=f(v)

(2)

式中，xr是检波点的空间坐标；pcal为模拟的地震压力波场；f为波动方程正演算子，即方程(1)。

全波形反演(FWI)通过最小化模拟数据和野外观测数据之间的误差，推导地下的速度参数，其目标函数通常定义为模拟数据和观测数据残差的L2范数

(3)

式中，ns和ng分别为炮点和检波点数目；pobs为野外观测的地震数据；tmax表示记录地震波的最大时间。

该目标函数受到模拟数据满足的波动方程的限制，我们采用拉格朗日乘子法法求解该约束性优化问题，建立拉格朗日乘子符为：

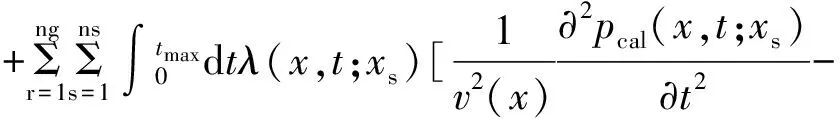
(4)

式中，λ(x,t；xs)为未知的拉格朗日乘子函数。目标函数的梯度表达式可以根据拉格朗日乘子符随速度的偏导数得到

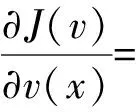
(5)

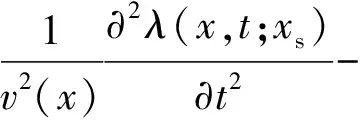
(6)

该伴随方程与声波方程(1)具有相同的表达形式，因此只需要将震源项替换为模拟数据和观测数据的残差，即可利用相同的数值求解方法模拟震源波场和伴随波场。

因此，传统的声波全波形反演的流程可以简述为：

1)沿时间正向求解方程(1)，得到正向传播的震源波场pcal(x,t；xs)，并保存所有时刻的正传波场在计算机内存中。

2)沿时间反方向求解方程(6)，得到反向传播的检波点波场λ(x,t；xs)。

3)从计算机内存中提取保存的波场，应用公式(5)，构建FWI的梯度。

4)采用合适的反演算法，计算优化的步长，更新速度参数v。

5)重复1～4步骤，直到目标函数值小于设定的值或满足最大迭代次数。

1.2 全波形反演的解析步长

上一节，我们已经推导了FWI的梯度，给出了传统FWI的实现流程。然而，为了得到合理的反演结果，最优化的搜索步长也尤其重要，常规的步长求取方法有很多，如：固定步长[14]、抛物线拟合[15]等方法。在每1次的迭代过程中，抛物线拟合的方法对每炮数据至少需要进行两次正演计算，才能够给出合理的步长，计算量过大。因此，本文采用解析步长的方法[16-17]，该方法仅需对每炮数据额外进行一次正演正演计算即可得到优化步长。

将第k+1次迭代的目标函数进行二阶泰勒展开，可得：

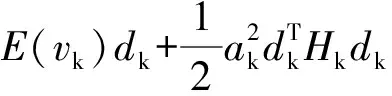
(7)

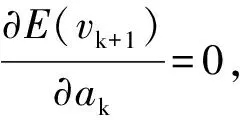
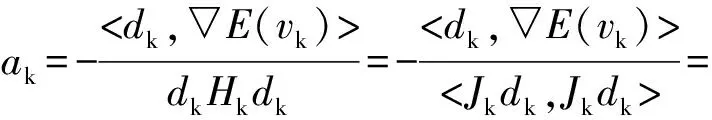
(8)

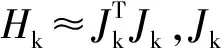
(9)

式中，f为式(1)所示的正演算子，ε为试探步长，它满足条件

(10)

1.3 混合共轭梯度方法

常规最速下降方法在迭代寻优的过程，收敛速度非常缓慢，会带来锯齿折叠效应。为了在迭代过程中，求解一个合理的下降方向dk，本文我们将一种混合类的共轭梯度方法应用到FWI方法中，以加速反演的收敛速度。第k次迭代的下降方向dk可以根据下列公式得到：

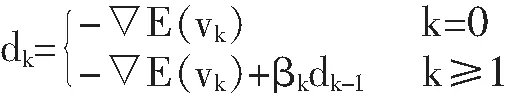
(11)

其中，βk满足[18-19]：

(12)

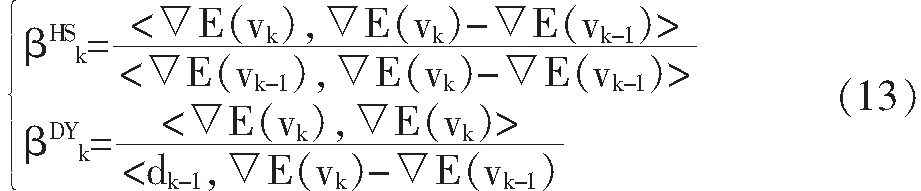
在得到共轭梯度方向和优化步长后，速度参数则能够迭代地更新，更新公式可以表示为：

vk+1=vk+αkdk

(14)

2 基于波场重建的时域FWI

在传统FWI的实现过程中，需要对背景震源波场和伴随波场进行零延迟互相关来构建梯度。但二者在时间方向上互逆，因此可预先保存某一方向所有时刻的波场值，当另一个波场传播时，提取相应时刻保存的波场进行互相关运算，但由此产生巨大的存储需求和I/O(Input/Output)耗时通常是难以接受的。因此，本文提出一种适用于FWI的逆时重建震源波场的方法，旨在降低了FWI方法的存储需求和I/O耗时。

本文采用高阶有限差分法求解波动方程(1)：

波动方程差分公式

p(x,z,t+Δt)=2p(x,z,t)-p(x,z,t-Δt)+

(15)

如图1所示，假设真实波场范围为图1中的A区域，如果采用空间12阶差分计算格式求解波动方程，仅需保存A区域外侧6层波场数据，如图1中B区域，即可满足差分条件，C区域为吸收边界区域。

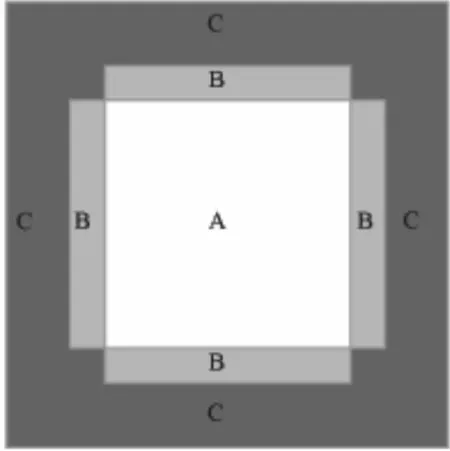
图1 边界存储示意图

为了实现震源波场的逆时重建，震源波场沿正向传播时，我们需要记录每时刻的B区域的波场信息以及最后时刻的A区域的波场信息。利用这些保存的信息，我们可以实现逆时波场重建：首先通过波动方程的逆向运算实现震源波场的逆时传播，同时，将对应时刻的B区域内的波场使用正传过程中保存的波场更新，以满足差分运算条件。在震源波场逆时重建过程中，结合公式5即可进行梯度的构建，直到所有时刻和所有炮完成叠加。其余反演步骤与传统方法一致，综上所述，本文提出的基于波场重建的时域FWI流程如图2所示。

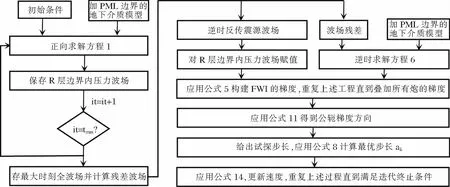
图2 基于波场重建的时域FWI流程

文中首先采用简单的均匀各向同性的介质进行震源波场逆时重建方法测试，该模型的水平和垂直方向网格点均为301，沿水平和垂直方向的网格尺寸均为10 m。该模型的纵波传播速度为2 800 m/s，为了吸收来自由于边界截断产生的反射波，我们应用了完美匹配层吸收边界(PML)[20]，吸收边界厚度为50个网格点。正演时，震源函数为主频20 Hz的雷克子波，该震源位于模型(1.5 km, 1.5 km)，时间步长为1 ms。

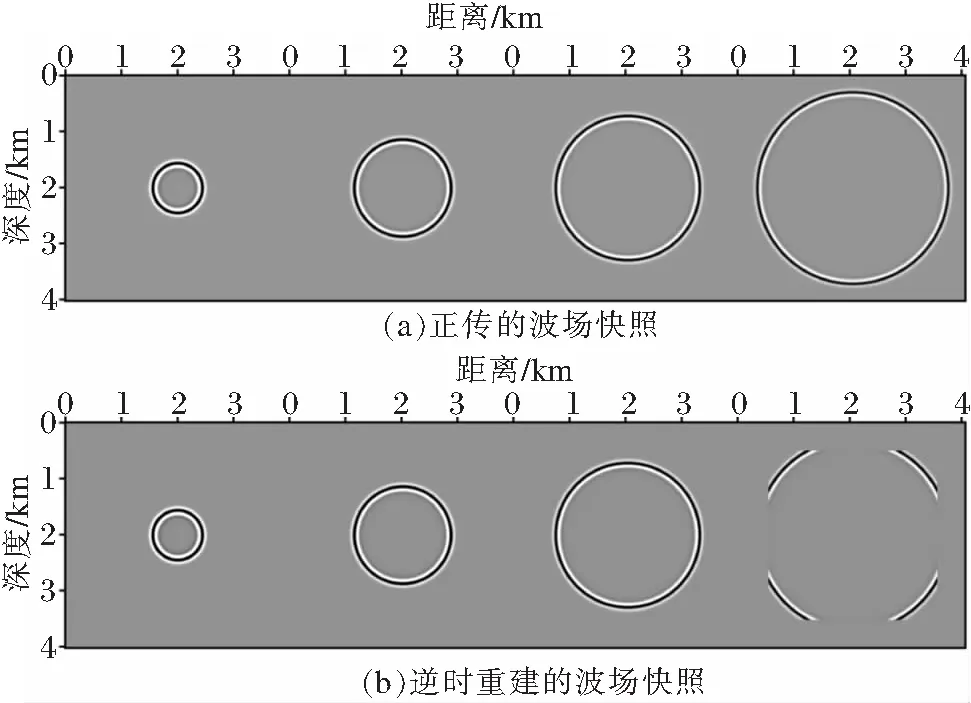
图3 均匀各向同性介质的波场快照(t=0.15，0.30，0.45，0.60 s)

图3为均匀各向同性介质不同时刻的波场快照，其中图3a和图3b分别显示了正向传播和本文方法逆时重建的震源波场，从左自右的时刻分别为0.15，0.30，0.45，0.60 s。我们不难发现，模型区域内的震源波场已经被很好地重建出来，由于PML边界内的波场不参与梯度的计算，因此并没有重建。我们进一步对波场快照抽取单道进行对比，正传波场和重建波场的单道数据对比如图4所示，抽取位置在t=0.45 s，x=2 km处。观察可知，正传的单道图4a和逆时重建的单道图4b几乎没有差别。两者的误差单道图4c所示，可知单道误差10-4的数量级。

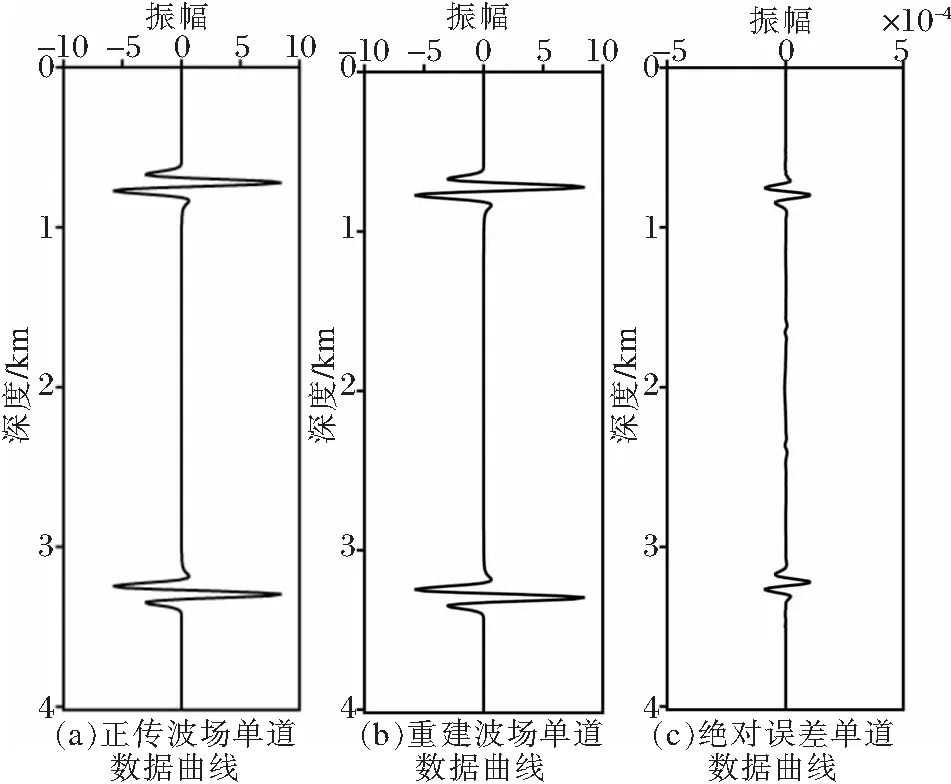
图4 正传及逆时重建的波场(t=0.45s)单道数据对比

为了证明文章中所述方法能够节约存储，我们对比了传统全波场存储的方法和文章所提出方法。假设，该模型的传播总时间间隔为5 000，波场数据在GPU端的数据类型为4字节浮点型，全波场存储的计算方法为：nx·hz·nt·4byte，本文的方法的存储为z·(nx+nz)·nt·6·4byte，其中6表示为有限差分方法的空间差分阶数的1/2，nx和nz为模型沿水平和垂直方向的空间网格点数。存储消耗对比如表1所示，这验证了本文所述方法能够大幅降低存储。特别地，当模型为3D时，文中所述的方法将大幅降低存储消耗，加速反演的计算速度。

表1 匀速模型波场重建存储消耗对比

3 模型测试

为了验证文中所述波场重建方法和全波形反演方法的有效性，分别对Marmousi2模型进行的波场重建测试和FWI方法测试。

3.1 波场重建方案测试

首先，进行了基于Marmousi2模型的波场重建测试，速度模型如图5所示。模型沿水平和垂直方向的网格点数分别为500和200，沿水平和垂直方向的网格间距均为10 m，为了压制了来自边界的虚假反射，我们在模型四周加载了厚度为50层PML吸收边界。震源位置位于水平方向2.5 km，垂直方向0.65 km处，震源函数为主频20 Hz的雷克子波，时间采样间隔为1 ms。

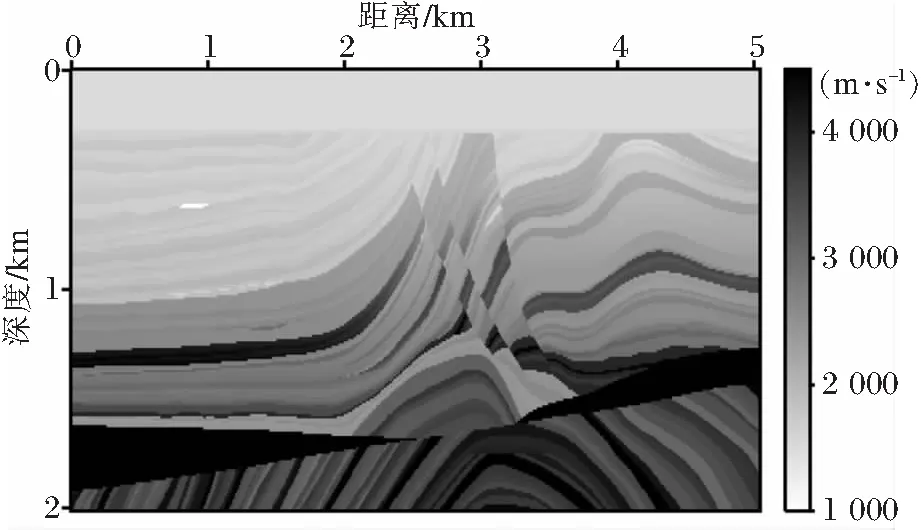
图5 Marmousi2 速度模型

分别截取正传至t=0.20，0.40，0.60，0.80 s时刻的震源波场，如图6a所示，当地震波传播至最大时刻5 s时，进行波场逆时重建，重建所得的t=0.20，0.40，0.60，0.80 s时刻的波场如图6b所示。根据图6对比可知，本文所述的逆时重建方法能够很好地恢复出在模型区域内的震源波场。进一步对波场快照抽取单道数据进行对比，所选数据为t=0.40 s，x=3 km处的波场数据，对比结果如图7所示。正传波场和逆时重建波场的的单道数据分别如图7a和7b所示，二者并无肉眼可见差别，对两者做相减运算，分析所得误差如图7c所示，误差为10-3数量级，与实际有效波振幅相差4个数量级，对真实结果无明显影响。本次测试中，基于Marmousi2模型的波场重建方案和传统全波场保存方案的存储消耗对比如表2所示，相比于全波场保存方案，本文方法能降低约90%的存储量，效果显著。

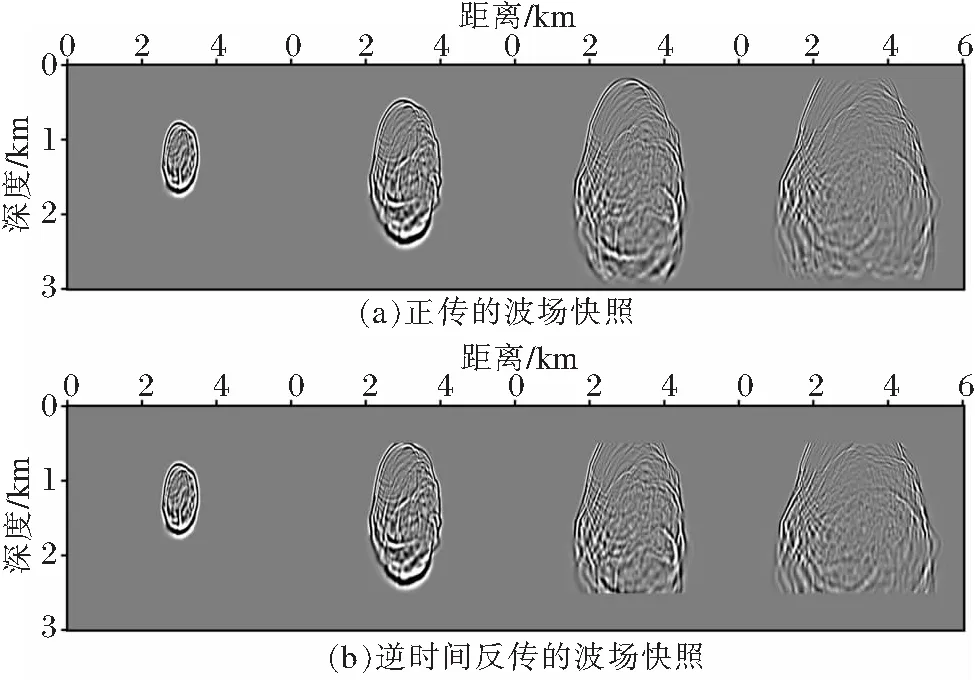
图6 Marmousi模型的波场快照(t=0.20，0.40，060，0.80 s)

图7 正传及逆时逆时反传的波场(t=0.45 s)单道对比

模型名称模型大小/m总时间间隔/s全波场存储/M边界存储/MMarmousi2500×20050001907160

3.2 Marmousi2全波形反演测试

为了验证本文提出的FWI方法对复杂模型的有效性，对Marmousi2模型进行了FWI测试，精确速度模型如图5所示。模型的基本信息与波场重建测试相同。震源和检波器均置于地面，震源的范围在0～5 km，炮间距为250 m，共20炮，采用主频为10 Hz的雷克子波，共500个检波器，检波点间距为10 m。时间采样间隔为1 ms，总时间长度为5 s。

由于实际地震勘探无法获得精确的速度模型，因此在进行FWI测试时，首先将图5所示的精确速度进行平滑，如图8所示，以此作为初始速度模型。不同迭代次数的反演结果如图9所示。随着迭代次数的增加，反演结果逐渐接近真实速度，对比不同迭代次数的反演结果可进一步发现，初期的反演结果对中浅部的速度构造更新效果较好，当迭代次数超过50次后，深层的速度构造也得以更新，趋近真实速度。

分别提取了水平方向1，2，3，4 km处的反演结果的单道数据，如图10所示，黑色实线表示初始速度，蓝色实线表示真实速度，绿色和红色实线分别表示迭代20次和100次的反演结果。曲线对比的结果与前文所述结论一致，执行20次迭代计算后，文中所述的方法可以很好地反演出中浅层的速度，随着迭代次数的增加，深层构造也得到了有效更新。图11显示了目标函数随迭代次数的下降情况，随着迭代计算，理论模拟数据与观测数据误差逐渐减少，进一步验证了本文方法的有效性。

图8 Marmousi 平滑速度模型

图9 不同迭代次数Marmousi的反演结果

图10 不同迭代次数的单道对比图

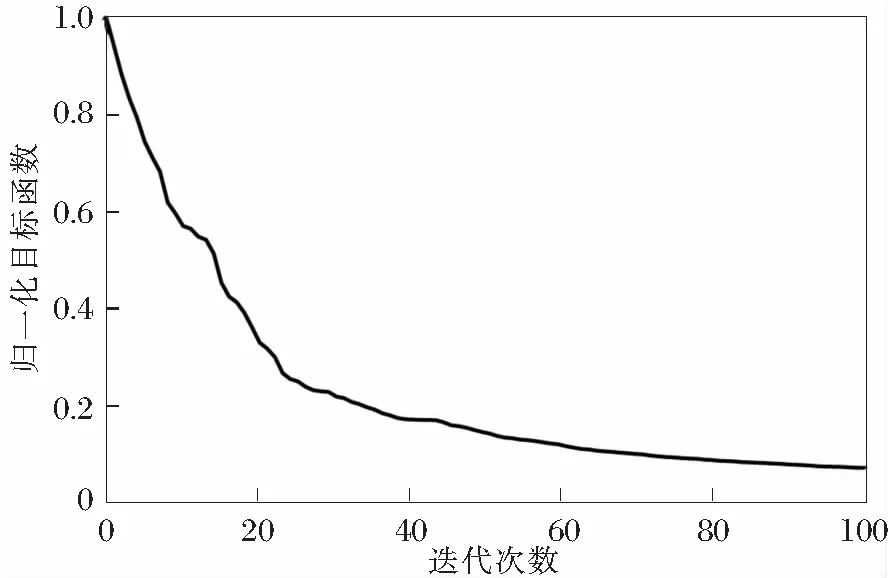
图11 目标函数随迭代次数的下降曲线

4 结 论

波场数据的存储策略对全波形反演方法的应用要求至关重要，本文从有限差分的原理出发，提出了保存局部波场数据的波场重建策略，能够大幅降低全波形反演的波场存储需求。多种模型试算也表明本文方法的正确性和有效性。

本文方法对基于复杂方程(如一阶速度应力方程和弹性波方程等)的FWI方法或三维FWI均具有一定的借鉴意义，这也是本文下一步的研究重点；本文提出的波场重建策略，仅适用于非损耗介质下的波场重建，对于粘性介质的波场重建方法仍有待进一步研究。

参考文献：

[1] Tarantola A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266.

[2] Pratt R G. Seismic waveform inversion in the frequency domain Part 1 theory and verification in a physical scale model[J]. Geophysics, 1999, 64(3): 888-901.

[3] Mora P. Inversion = migration + tomography[J]. Geophysics, 1989, 54(12): 1575-1586.

[4] Wang H, Singh S C, Audebert F, et al. Inversion of seismic refraction and reflection data for building long-wavelength velocity models[J]. Geophysics, 2015, 80(2): R81-R93.

[5] Pratt R G, Shin C, Hick G J, et al. Gauss Newton and full Newton methods in frequency-space seismic waveform inversion[J]. Geophysical Journal International, 1998, 133(2): 341-362.

[6] Bunks C, Saleck F M, Zaleski S, et al. Multiscale seismic waveform inversion[J]. Geophysics, 1995; 60(5): 1457-1473.

[7] Clapp R G. Reverse time migration with random boundarie[J]. Seg Technical Program Expanded Abstracts, 2009, 2809-2813.

[8] Shen X, Clapp R G. Random boundary condition for memory-efficient waveform inversion gradient computation[J]. Geophysics, 2015, 80(6): R351-R359.

[9] Clapp R G. Reverse time migration: Saving the boundaries[J]. Stanford Exploration Project, 2008,136-144.

[10] 王保利, 高静怀, 陈文超,等. 地震叠前逆时偏移的有效边界存储策略[J]. 地球物理学报, 2012, 55(7): 412-2421.

[11] Yang P, Gao J, Wang B, et al. RTM using effective boundary saving: A staggered grid GPU implementation[J]. Computers & Geosciences, 2014; 64-72.

[12] FENG Bo, WANG Huazhong. Reverse time migration with source wavefield reconstruction strategy[J]. Journal of Geophysics and Engineering, 2012, 9(1): 69-74.

[13] Kalita M, Alkhalifah T. Efficient full waveform inversion using the excitation representation of the source wavefield[J]. Geophysical Journal International, 2017, 210(3): 581-1594.

[14] Kohn D, De Nil D, Kurzmann A, et al. On the influence of model parametrization in elastic full waveform tomography[J]. Geophysical Journal International, 2012, 191(1): 325-345.

[15] Vigh D, Starr E W. 3D prestack plane-wave, full-waveform inversion[J]. Geophysics, 2008, 73(5): VE135-VE144.

[16] Gauthier O, Virieux J, Tarantola A, et al. Two-dimensional nonlinear inversion of seismic waveforms: Numerical results[J]. Geophysics, 1986, 51(7): 1387-1403.

[17] Pica A, Diet J P, Tarantola A, et al. Nonlinear inversion of seismic reflection data in a laterally invariant medium[J]. Geophysics, 1990; 55(3): 284-292.

[18] Hager W W, Zhang H. A survey of nonlinear conjugate gradient methods[J]. Pacific Journal of Optimization, 2006, 2(1): 35-58.

[19] Yang P, Gao J, Wang B, et al. A graphics processing unit implementation of time-domain full-waveform inversion[J]. Geophysics, 2015, 80(3): F31-F39.

[20] 王守东. 声波方程完全匹配层吸收边界[J]. 石油地球物理勘探, 2003, 38(1):31-34.