基于储层厚度特征的油藏建模粗化方法研究

张学娟，刘如昊，张 曦，郭天然

(1. 东北石油大学 非常规油气成藏与开发省部共建国家重点实验室，黑龙江 大庆 163318； 2. 西南油气田分公司 工程技术研究院，四川 成都 610017； 3. 吉林油田分公司 油气工程研究院，吉林 松原 138000)

1 网格粗化方法

油藏模型网格粗化的目的是降低网格数、减少数值模拟的计算量[1]，以保证在现有计算能力水平下，能够在有限的时间内实现数值模拟的拟合计算。模型粗化过程中应在实现提高计算效率的前提下，保证粗化后的模型能够尽量真实的反映原始精细模型的必要地质信息。

影响网格粗化精度的主要因素一般来说主要有两个方面：一是粗化网格的尺寸；二是网格粗化的算法[2]。粗化网格尺寸的最小程度主要依赖于计算能力的发展水平，而对于不同储层厚度特征的地质模型采用适合的粗化算法可以使有效地质信息的损失量降至最低。目前油藏模型网格粗化方法的主要思路都是用一个等效的均质粗网格单元去取代原模型中多个非均质的细网格单元，从物性参数上讲, 也就是用一个平均值去代替多个不同的值, 所以油藏模型网格粗化的本质特征是求均值[3]。实际工作中常用的粗化算法包含算术平均法、几何平均法、调和平均法、幂指数平均法和均方根等简单平均算法[4-5]。各种不同的平均算法都可以采用简单加权参数进行加权平均，比如可以按照网格长度、网格厚度、网格面积、网格体积等不同的加权平均方法[6-10]，本文研究的是按照网格尺寸和网格体积综合加权平均的算法对油藏模型网格进行粗化。

2 研究区储层参数特征

油藏模型粗化参数在兼顾计算效率的前提下，首先需要考虑垂向网格参数是否能够精细刻画储层与非储层的分界面，此时应考虑垂向采样参数与储层厚度的关系。

图1 萨II油层组砂岩厚度统计规律

研究区位于松辽盆地北部，目的层为萨尔图油层，按着砂岩厚度分类统计砂岩累计频数，并绘制统计直方图(如图1)。统计结果表明：研究区目的层主要以薄层为主，大部分单层砂岩厚度小于1 m，为了使精细模型能够反映储层内部物性变化，以及厚度为0.2 m的泥岩夹隔层信息，研究区精细模型网格垂向尺寸设置为0.1 m，以此保证精细模型能够较准确的反应储层内部物性的垂向变化信息。

3 不同网格垂向粗化算法粗化模型的误差分析

本次研究保留精确模型平面的特征，仅在垂向上开展不同粗化算法对属性模型精确程度的影响分析(如图2)。在保证了平面的网格精度不变的情况下，分别采用算术平均法，几何平均法，调和平均法、幂指数平均法以及均方根平均法对研究区精细模型进行粗化，垂向粗化网格尺寸为0.4 m，分别统计井点处属性值、小层属性平均值以及粗化前后模型储量变化，对比5种方法粗化后的模型与原始精细模型的误差，筛选适用于本研究区的最优垂向粗化算法。

图2 垂向精细地质模型粗化示意

3.1 单点误差分析

某一深度点上精细模型网格属性值与对应位置粗化网格属性值的相对误差为单点误差。选取研究区数据完备、位置均匀分布的八口井所经过的模型网格，统计网格各属性值单点误差，并按沉积小层求取各属性单点误差平均值(图3～5)。单点平均误差分析结果表明，各算法粗化结果在各沉积小层内误差特征存在差异，但算数平均法在各小层均表现出较稳定的低误差特征。各算法粗化结果在不同沉积单元误差特征存在差异的主要原因是，由于各沉积小层之间薄储层组合特征的差别导致；而算数平均算法薄储层组合特征的变化并不影响该算法低误差的特征。在研究区垂向网格粗化过程中，应用算数平均法进行粗化可以较好的保留原始精细模型地质特征。

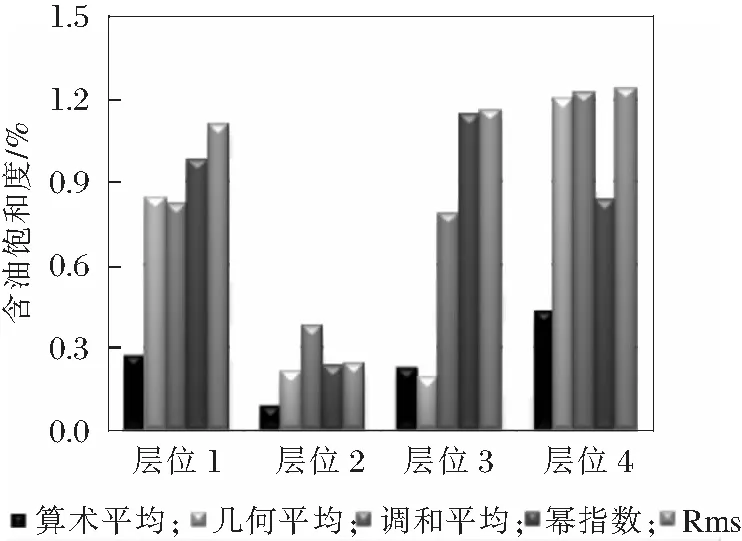
图3 饱和度模型小层平均误差

图4 孔隙度模型小层平均误差

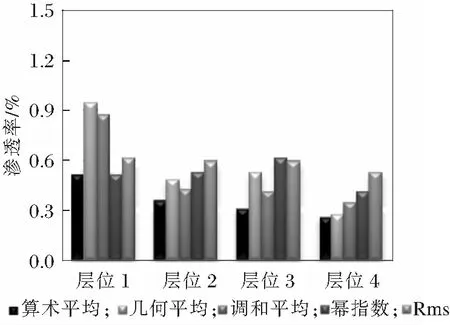
图5 渗透率模型小层平均误差

3.2 储量误差分析

在构造格架信息及储层结构信息可靠的前提下，粗化模型储量与精细模型储量的误差，再一定程度上反映了粗化模型的精度。地质模型储量误差是衡量粗化模型精确程度、保证后续油藏数值模拟结果稳定可靠的一个重要指标参数。按各小层沉积单元分别统计五种不同的算法粗化模型的储量误差，统计结果如(图6)。储量误差统计结果表明，算数平均法粗化结果储量误差最小。

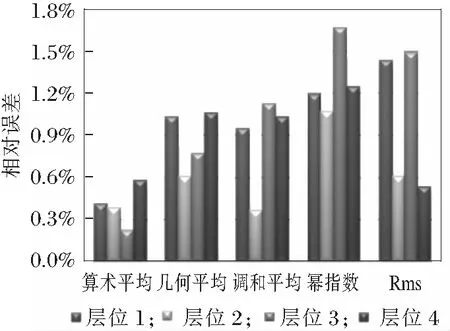
图6 各小层储量平均误差

4 结 语

通过不同算法各小层模型粗化结果误差统计分析表明，对于薄储层(储层厚度1 m左右)特征的地层，算法相同情况下，模型粗化结果的精确程度受储层厚度及储层垂向分布的差异影响。对比算数平均法、调和平均法、几何平均法、幂指平均法以及均方根平均法粗化结果表明，对于薄储层特征地层，算数平均法粗化结果综合表现出较稳定的低误差特征，是适合于研究区地质情况的粗化算法。

参考文献：

[1] 马远乐, 赵刚. 油藏地质模型数据体粗化技术[J]. 清华大学学报(自然科学版), 2000, 40(12):37-39.

[2] 刘慧卿, 马代鑫, 张松亭. 精细油藏描述数据的粗化方法研究[J]. 中国石油大学学报(自然科学版), 2003, 27(6):36-38.

[3] 何吉祥.储层精细地质模型合理粗化程度研究[D].成都：西南石油大学，2011.

[4] Barker J W. A Critical review of the use of pseudorelative permeabilities for upscaling SPE reservoir engineering[J]. Society of Petroleum Engineers, 1997:138-143.

[5] 孙致学，鲁洪江，孙治雷. 油藏精细地质模型网格粗化算法及其效果[J].地质力学学报，2007，13(4)：368-375.

[6] 朱绍鹏，张辉，李茂.网格粗化技术对油藏数值模拟的影响[J].中国海上油气，2008，20(5)：319-321.

[7] Christie M A. Upscaling for reservoir simulation[J]. Journal of Petroleum Technology, 1996, 48(11):1004-1010.

[8] Chawathe A, Taggart I. Insights into upscaling using 3D streamlines[J]. Spe Reservoir Evaluation & Engineering, 2004, 7(4):285-296.

[9] 李福垲, 由军, 陈立生. 地质模型网格粗化合并技术[J]. 石油勘探与开发, 1996, 23(3): 76-79.

[10] Merchan S, Srinivasan S. Upscaling using a nonuniform coarsened grid with optimum power average[J]. Journal of Canadian Petroleum Technology, 2007, 46(7)：21-29.